frecuencias

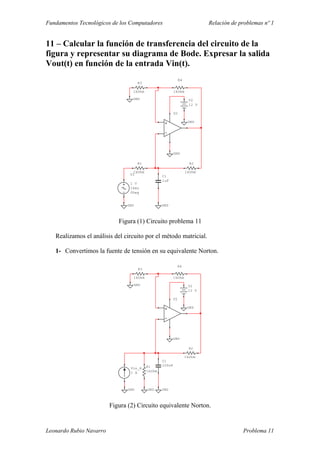
1. Fundamentos Tecnológicos de los Computadores Relación de problemas nº 1
11 – Calcular la función de transferencia del circuito de la
figura y representar su diagrama de Bode. Expresar la salida
Vout(t) en función de la entrada Vin(t).
U2
R1
1kOhm
R2
1kOhm
R3
1kOhm
R4
1kOhm
C1
1uF
GND
GND
V1
1 V
1kHz
0Deg
GND
GND
V2
12 V
GND
Figura (1) Circuito problema 11
Realizamos el análisis del circuito por el método matricial.
1- Convertimos la fuente de tensión en su equivalente Norton.
U2
R1
1kOhm
R2
1kOhm
R3
1kOhm
R4
1kOhm
C1
100nF
GND
GND
GND
V2
12 V
GND
GND
Vin_R
1 A
GND
Figura (2) Circuito equivalente Norton.
Leonardo Rubio Navarro Problema 11

2. Fundamentos Tecnológicos de los Computadores Relación de problemas nº 1
2- Calculamos la matriz asociada al circuito.














=










−−
−
−+
0
0
2
20
02
3
2
1
R
Vin
V
V
V
GGG
GG
GCsG
3- Aplicando cortocircuito virtual tenemos que V2(entrada inversora)=V1(entrada
no inversora). Por lo tanto sumamos la columna 2 a la columna 1 y la colocamos
en la columna 1. Ya podemos tachar la columna 2 y eliminar la su incógnita.














=










−−
−
−+
0
0
2
20
02
3
2
1
R
Vin
V
V
V
GGG
GG
GCsG
Nueva matriz














=










−
−
−+
0
0
22
2
2
3
1
R
Vin
V
V
GG
GG
GCsG
4- Eliminamos la fila correspondiente a la salida del Amplificador operacional (fila
3ª).














=










−
−
−+
0
0
22
2
2
3
1
R
Vin
V
V
GG
GG
GCsG
La matriz final asociada al circuito será:
Leonardo Rubio Navarro Problema 11
C1+C2

3. Fundamentos Tecnológicos de los Computadores Relación de problemas nº 1








=







−
−+
02
2
3
1
R
Vin
V
V
GG
GCsG
Por lo tanto, la salida del circuito Vout será igual a calcular el valor de V3 en la matriz
asociada al circuito:
RCs
Vin
Cs
R
Vin
GGCsG
R
Vin
G
GG
GCsG
G
R
Vin
CsG
V
2
2
22
2
2
2
02
2
223 ==
+−−
−
=






−
−+








+
=
RCs
Vin
Vout
2
=
La función de transferencia del circuito es la siguiente:
RCsVin
Vout
sH
2
)( ==
A partir de la función de transferencia dibujamos el diagrama de bode.
CRw
j
jRCwRCs
sH
222
)( −===
)log(20)2log(20)2log(20)2log(20)2log(20)(log20)( fRCRCfsHfA −−=−== ππ
Para poder representar numéricamente el diagrama de bode, damos valores a R y C.
R = 1 KΩ
C = 100 nF
Calculamos la magnitud para unos valores de frecuencia determinados.
Frecuencia Amplitud
1 Hz 70 dB
10 Hz 50 dB
100 Hz 30 dB
1 KHz 10 dB
10 KHz -10 dB
100 KHz -30 dB
Tabla (1) Magnitud
Leonardo Rubio Navarro Problema 11

4. Fundamentos Tecnológicos de los Computadores Relación de problemas nº 1
Magnitud
70
50
30
10
-10
-30
-40
-20
0
20
40
60
80
1 Hz 10 Hz 100 Hz 1 KHz 10 KHz 100 KHz
Frecuencia
Ganancia(dB)
Gráfica (1) Magnitud del diagrama de Bode
En el caso de la fase, se mantiene constante con un valor de
2
π
−
Fase
-100
-90
-80
-70
-60
-50
-40
-30
-20
-10
0
1 Hz 10 Hz 100 Hz 1 KHz 10 KHz 100 KHz
Frecuencia
Fase(Grados)
Gráfica (2) Fase del diagrama de Bode
Leonardo Rubio Navarro Problema 11

5. Fundamentos Tecnológicos de los Computadores Relación de problemas nº 1
Expresar la salida Vout(t) en función de la entrada Vin(t).
RCs
sVin
sVout
)(·2
)( =
Aplicamos la transformada inversa de laplace.
∫=



=



= −−
t
dttVin
RCs
sVin
L
RCRCs
sVin
LtVout
0
11
)(
2)(
·
2)(·2
)(
∫=
t
dttVin
RC
tVout
0
)(
2
)(
Leonardo Rubio Navarro Problema 11

6. Fundamentos Tecnológicos de los Computadores Relación de problemas nº 1
Expresar la salida Vout(t) en función de la entrada Vin(t).
RCs
sVin
sVout
)(·2
)( =
Aplicamos la transformada inversa de laplace.
∫=



=



= −−
t
dttVin
RCs
sVin
L
RCRCs
sVin
LtVout
0
11
)(
2)(
·
2)(·2
)(
∫=
t
dttVin
RC
tVout
0
)(
2
)(
Leonardo Rubio Navarro Problema 11