Para sumar o restar fracciones, es necesario que tengan el mismo denominador (partición común) dividiendo las unidades en partes iguales al denominador de la otra fracción. Al multiplicar fracciones, se multiplican los numeradores y los denominadores por separado, encontrando la región en común entre las dos fracciones.

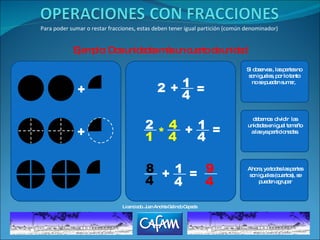
1. Para poder sumar o restar fracciones, estas deben tener igual partición (común denominador) Ejemplo: Dos unidades más un cuarto de unidad 2 + __ 1 4 = + __ 1 4 = __ 4 4 __ 2 1 * + __ 1 4 = __ 8 4 __ 9 4 Si observas , las partes no son iguales, por lo tanto no se pueden sumar, debemos dividir las unidades en igual tamaño a las ya particionadas. Ahora, ya todas las partes son iguales (cuartos), se pueden agrupar + + Licenciado. Juan Andrés Galindo Cepeda

2. Para poder sumar o restar fracciones, estas deben tener igual partición (común denominador) Ejemplo: Dos unidades menos un cuarto de unidad 2 - __ 1 4 = - __ 1 4 = __ 4 4 __ 2 1 * - __ 1 4 = __ 8 4 __ 7 4 Si observas , las partes no son iguales, por lo tanto no se pueden restar, debemos dividir las unidades en igual tamaño a las ya particionadas. Ahora, ya todas las partes son iguales (cuartos), se pueden restar - - Licenciado. Juan Andrés Galindo Cepeda

3. Para poder sumar o restar fracciones, estas deben tener igual partición (común denominador) Ejemplo: Dos tercios de unidad más tres cuartos de unidad + __ 3 4 = + = __ 4 4 __ 2 3 * + __ 9 12 = __ 8 12 __ 17 12 Si observas , las partes no son iguales, por lo tanto no se pueden sumar, debemos dividir todas las partes en igual tamaño. Ahora, ya todas las partes son iguales (doceavos), se pueden sumar + + __ 2 3 __ 3 3 __ 3 4 * Licenciado. Juan Andrés Galindo Cepeda

4. En la multiplicación de fracciones se busca las partes que son comunes (intersección) Ejemplo: Cuatro quintos de unidad por dos tercios de unidad Licenciado. Juan Andrés Galindo Cepeda = __ 2 3 __ 4 5 * __ 8 15 _____ 4*2 5*3 * = = Al multiplicar dos fracciones , el resultado es la región en común. Para realizar la multiplicación de dos números fraccionarios, debemos multiplicar directamente numeradores entre si y denominadores entre si. Si analizas un poco, al multiplicar cuatro quintos por dos tercios, debemos tomar cada quinto y dividirlo en tres partes iguales y tomar solamente dos. Sumamos las partes de cada quinto nos da ocho de un total de quince partes iguales. ¿Podríamos hacerlo al revés, tomar cada tercio y dividirlo en cinco partes iguales y …?