Investigacion de operaciones problemas1
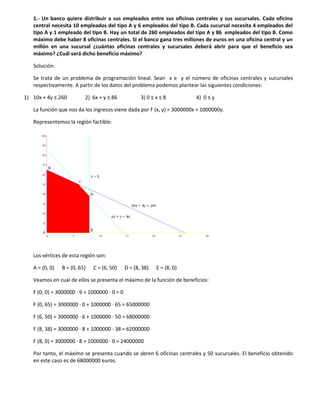
- 1. 1.- Un banco quiere distribuir a sus empleados entre sus oficinas centrales y sus sucursales. Cada oficina central necesita 10 empleados del tipo A y 6 empleados del tipo B. Cada sucursal necesita 4 empleados del tipo A y 1 empleado del tipo B. Hay un total de 260 empleados del tipo A y 86 empleados del tipo B. Como máximo debe haber 8 oficinas centrales. Si el banco gana tres millones de euros en una oficina central y un millón en una sucursal ¿cuántas oficinas centrales y sucursales deberá abrir para que el beneficio sea máximo? ¿Cuál será dicho beneficio máximo? Solución: Se trata de un problema de programación lineal. Sean x e y el número de oficinas centrales y sucursales respectivamente. A partir de los datos del problema podemos plantear las siguientes condiciones: 1) 10x + 4y ≤ 260 2) 6x + y ≤ 86 3) 0 ≤ x ≤ 8 4) 0 ≤ y La función que nos da los ingresos viene dada por F (x, y) = 3000000x + 1000000y. Representemos la región factible: Los vértices de esta región son: A = (0, 0) B = (0, 65) C = (6, 50) D = (8, 38) E = (8, 0) Veamos en cual de ellos se presenta el máximo de la función de beneficios: F (0, 0) = 3000000 · 9 + 1000000 · 0 = 0 F (0, 65) = 3000000 · 0 + 1000000 · 65 = 65000000 F (6, 50) = 3000000 · 6 + 1000000 · 50 = 68000000 F (8, 38) = 3000000 · 8 + 1000000 · 38 = 62000000 F (8, 0) = 3000000 · 8 + 1000000 · 0 = 24000000 Por tanto, el máximo se presenta cuando se abren 6 oficinas centrales y 50 sucursales. El beneficio obtenido en este caso es de 68000000 euros.
- 2. 2. En una ebanistería se fabrican dos tipos de mesas: mesas de comedor y mesas para ordenador. Las mesas de comedor necesitan 4 m2 de madera y las mesas para ordenador 3 m2. El fabricante dispone de 60 m2 de madera y decide confeccionar al menos 3 mesas de comedor y al menos el doble de mesas de ordenador que de mesas de comedor. Además, por cada mesa de ordenador obtiene un beneficio de 200 €, mientras que obtiene un beneficio de 300 € por cada mesa de comedor. ¿Cuántas mesas de cada tipo debe fabricar para obtener el beneficio máximo? Condiciones: 1) 4x + 3y ≤ 60 2) x ≥ 3 3) y ≥ 2x La función del beneficio obtenido por el fabricante es: F (x, y) = 200x + 300y Dibujemos la región factible: Los vértices de esta región son los puntos: A = (3, 6) B = (3, 16) C = (6, 12) Sustitución de los valores de los vértices en la función objetivo. a) F (3, 6) = 200 · 3 + 300 · 6 = 2400 b) F (3, 16) = 200 · 3 + 300 · 16 = 5400 c) F (6, 12) = 200 · 6 + 300 · 12 = 4800 Beneficio máximo es de 5400 euros y se consigue elaborando 3 mesas de comedor y 16 mesas de ordenador.
- 3. 3. El club “Amigos del Románico” quiere organizar un viaje visitando el románico de Castilla y León para sus 200 socios. Acude para ello a una agencia de viajes que dispone de 4 microbuses de 25 plazas y 5 autobuses de 50 plazas, pero sólo dispone de 6 conductores. El alquiler de un autobús es de 160 euros por día, mientras que el alquiler de un microbús es de 70 euros por día. Con esas condiciones, ¿cómo deben organizar el viaje para que el coste del viaje sea el menor posible? Condiciones: 1) 0 ≤ x ≤ 4 2) 0 ≤ y ≤ 5 3) x + y ≤ 6 4) 25x + 50y ≥ 200 La función es: F (x, y) = 70x + 160y Dibujemos la región factible: Los vértices de esta región son los puntos: 1) A = (0, 4) 2) B = (0, 5) 3) C = (1, 5) 4) D = (4, 2) Sustitución de los valores de los vértices en la función objetivo. F (0, 4) = 70 · 0 + 160 · 4 = 640 F (0, 5) = 70 · 0 + 160 · 5 = 800 F (1, 5) = 70 · 1 + 160 · 5 = 870 F (4, 2) = 70 · 4 + 160 · 2 = 600 El costo mínimo es de 600 euros y donde se consigue contratando 4 microbuses y 2 autobuses.
- 4. 4. En una factoría, se desean producir al menos 4 unidades del producto B. Cada unidad de producto B ocupa un metro cúbico de espacio de almacenamiento, lo mismo que cada unidad de producto A. Tan solo disponemos de un almacén con capacidad de 20 metros cúbicos. Juan se encarga de una fase de la producción y Pedro de otra fase de la producción. Cada unidad de A requiere 4 horas de trabajo de Juan y 2 horas de trabajo de Pedro. Cada unidad de B requiere 1 hora de trabajo de Juan y 3 horas de trabajo de Pedro. Juan debe trabajar al menos 32 horas y Pedro al menos 36 horas. Cada unidad de producto A produce un beneficio de 25 euros y cada unidad de B produce un beneficio de 20 euros. Utilizando técnicas de programación lineal, calcula el número de unidades de producto A y de producto B que permiten obtener mayores beneficios, así como el beneficio máximo que se puede conseguir. Restricciones: 1) y ≥ 4 2) x + y ≤ 20 3) 4x + y ≥ 32 4) 2x + 3y ≥ 36 5) 0 ≤ x ≤ 20 6) y ≤ 20 Función objetivo: F (x, y) = 25x + 20y Los vértices son: a) A = (6, 8) b) B = (4, 16) c) C = (16, 4) d) D = (12, 4) Sustitución de los valores de los vértices en la función objetivo. F (6, 8) = 25 * 6 + 20 * 8 = 310 F (4, 16) = 25 * 4 + 20 * 16 = 420 F (16, 4) = 25 * 16 + 20 * 4 = 480 F (12, 4) = 25 * 12 + 20 * 4 = 380 El Beneficio Máximo es de 480 euros. Se produce cuando se fabrican 4 unidades del producto A y 16 del producto B.
- 5. 5. Una fábrica produce mermelada de naranja y de ciruela. El doble de la producción de mermelada de ciruela es menor o igual que la producción de mermelada de naranja más 800 cajas. También, se sabe que el triple de la producción de mermelada de naranja más el doble de la producción de mermelada de ciruela es menor o igual que 2400 cajas. Cada caja de mermelada de naranja produce un beneficio de 40 euros y cada caja de mermelada de ciruela 50 euros. Utilizando técnicas de programación lineal, ¿cuántas cajas de cada tipo de mermelada se han de producir para obtener un beneficio máximo? Calcula el beneficio máximo. Condiciones: 1) 2y ≤ x + 800 2) 3x + 2y ≤ 2400 3) x ≥ 0 4) y ≥ 0 La función es: F (x, y) = 40x + 50y Los vértices son: 1) A = ( 0, 0) 2) B = (0, 400) 3) C = (400, 600) 4) D = (800, 0) Sustitución de los valores de los vértices en la función objetivo. F (0, 0) = 40 · 0 + 50 · 0 = 0 F (0, 400) = 40 · 0 + 50 · 400 = 20000 F (400, 600) = 40 · 400 + 50 · 600 = 46000 F (800, 0) = 40 · 800 + 50 · 0 = 32000 Beneficio máximo es de 46000 euros y se produce elaborando 400 cajas de mermelada de naranja y 600 cajas de mermelada de ciruela.
- 6. 6. Cada instalación de una televisión analógica necesita 10 metros de cable y cada instalación de televisión digital necesita 20 metros. Cada televisión analógica necesita 20 minutos de instalación y 30 minutos cada televisión digital. Disponemos un máximo de 400 metros de cable al día. Tenemos que trabajar al menos 300 minutos al día. Diariamente podemos instalar un máximo de 20 televisiones analógicas y debemos instalar al menos 6 televisiones digitales. Por cada televisión analógica instalada obtenemos unos ingresos de 10 euros y por cada televisión digital 15 euros. Utilizando técnicas de programación lineal, representa la región factible, calcula el número de televisores analógicos y digitales que permiten obtener mayores ingresos diariamente, así como el ingreso máximo diario que se puede conseguir. Condiciones: 1) 10x + 20y ≤ 400 2) 20x + 30y ≥ 300 3) 0 ≤ x ≤ 20 4) 6 ≤ y ≤ 20 5) y ≤ 20 La Función es: F (x, y) = 10x + 15y. Los vértices de esta región son: A = (0, 10) B = (0, 20) C = (20, 10) D = (20, 6) E = (6, 6) Sustitución de los valores de los vértices en la función objetivo. F (0, 10) = 10 · 0 + 15 · 10 = 150 F (0, 20) = 10 · 0 + 15 · 20 = 300 F (20, 10) = 10 · 20 + 15 · 10 = 350 F (20, 6) = 10 · 20 + 15 · 6 = 290 F (6, 6) = 10 · 6 + 15 · 6 = 150 Por tanto, el máximo se presenta cuando se instalan 20 televisores analógicos y 10 televisores digitales. El beneficio obtenido en este caso es de 350 euros.
- 7. 7. Una fábrica de papel tiene almacenados 4000 Kg de pasta de papel normal y 3000 Kg de pasta de papel reciclado. La fábrica produce dos tipos de cajas de cartón. Para el primer tipo se utilizan 0,2 Kg de pasta de papel normal y 0,1 Kg de pasta de papel reciclado, mientras que para la caja del segundo tipo se utilizan 0,2 Kg de pasta de papel normal y 0,3 Kg de pasta de papel reciclado. Los beneficios que la fábrica obtiene por la venta de cada caja son, respectivamente 5 € para el primer tipo y 6 € para el segundo tipo de cajas. Utilizando técnicas de programación lineal, calcula cuántas cajas de cada tipo deben fabricar para obtener el máximo beneficio. ¿A cuánto asciende el beneficio máximo obtenido? Restricciones: 1) 0,2x + 0,2y ≤ 4000 2) 0,1x + 0,3y ≤ 3000 3) x ≥ 0 4) y ≥ 0 La función: F (x, y) = 5x + 6y. Los vértices son: 1) O = (0, 0) 2) A = (20000, 0) 3) B = (15000, 5000) 4) C = (0, 10000) Sustitución de los valores de los vértices en la función objetivo. F (0, 0) = 5 * 0 + 6 * 0 = 0 F (20000, 0) = 5 *20000 + 6 * 0 = 100000 F (15000, 5000) = 5 * 15000 + 6 * 5000 = 105000 F (0, 10000) = 5 *0 + 6 * 10000 = 60000
- 8. Beneficio máximo es de 105000 euros (€) .Se produce cuando se fabrican 15000 cajas del primer tipo y 5000 cajas del segundo tipo. 8. Una ONG organiza un convoy de ayuda humanitaria con un máximo de 27 camiones, para llevar agua potable y medicinas a una zona devastada por unas inundaciones. Para agua potable dedica un mínimo de 12 camiones y para medicinas debe dedicar un número de camiones mayor o igual que la mitad del número de camiones dedicados a llevar agua. Enviar un camión con agua potable tiene un coste de 9000 euros, mientras que el coste para un camión de medicinas es de 6000 euros. Calcula, utilizando técnicas de programación lineal, cómo debe organizarse el convoy para que su coste sea mínimo ¿Cuánto es el coste de la solución óptima? Restricciones: 1) x + y ≤ 27 2) x ≥ 12 3) y ≥ x/2 La función es: F (x, y) = 9000x + 6000y. Representemos la región factible: Los vértices son: 1) A = (12, 15) 2) B = (12, 6) 3) C = (18, 9) Sustitución de los valores de los vértices en la función objetivo. F (12, 15) = 9000 · 12 + 6000 · 15 = 198000 € F (12, 6) = 9000 · 12 + 6000 · 6 = 144000 € F (18, 9) = 9000 · 18 + 6000 · 9 = 216000 € La solución óptima es el del costo mínimo de 144000 euros (€). Se produce cuando 12 camiones para agua potable y 6 camiones para medicinas.
- 9. 9. Una fábrica de plásticos pretende fabricar nuevos productos nuevos productos platicos mezclando dos compuestos químicos A y B. Cada litro de producto plástico 1 lleva 2/5 partes del compuesto A y 3/5 partes del compuesto B, mientras que el producto plástico 2 lleva una mitad del compuesto A y la otra mitad del compuesto B.
- 10. 10. Como cada año, al inicio del curso académico, una tienda de material escolar prepara una oferta de 600 cuadernos, 500 carpetas y 400 bolígrafos para los alumnos de un IES, empaquetando el material de dos formas distintas. El primer paquete contiene 2 cuadernos, 1 carpeta y 2 bolígrafos, mientras que el segundo contiene 3 cuadernos, 1 carpeta y 1 bolígrafo. El primer paquete se vende al precio de 6.50 euros, mientras que el segundo se vende a 7 euros. Usando técnicas de programación lineal, ¿cuántos paquetes de cada tipo han de realizar para obtener la máxima recaudación? ¿A cuánto asciende dicha recaudación? Condiciones: 1) 2x + 3y ≤ 600 2) x + y ≤ 500 3) 2x + y ≤ 400 4) x ≥ 0 5) y ≥ 0 La función es: F (x, y) = 6,50x + 7y Los vértices son: 1) O = (0, 0) 2) A = (0, 200) 3) B = (150, 100) 4) C = (200, 0) Sustitución de los valores de los vértices en la función objetivo. F (0, 0) = 6,50 · 0 + 7 · 0 = 0 F (0, 200) = 6,50 · 0 + 7 · 200 = 1400 F (150, 100) = 6,50 · 150 + 7 · 100 = 1675 F (200, 0) = 6,50 · 200 + 7 · 0 = 1300 La máxima recaudación es de 1675 euros y se produce elaborando 150 paquetes del primer tipo (2 cuadernos, 1 carpeta y 2 bolígrafos) y 100 paquetes del segundo tipo (3 cuadernos, 1 carpeta y 1 bolígrafo).
