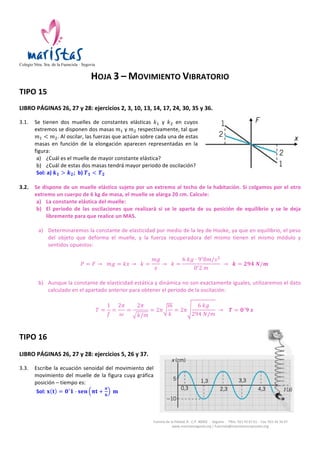
1.
Colegio Ntra. Sra. de la Fuencisla · Segovia
Camino
de
la
Piedad,
8
-­‐
C.P.
40002
-­‐
Segovia
-­‐
Tlfns.
921
43
67
61
-­‐
Fax:
921
44
34
47
www.maristassegovia.org
|
fuencisla@maristascompostela.org
HOJA
3
–
MOVIMIENTO
VIBRATORIO
TIPO
15
LIBRO
PÁGINAS
26,
27
y
28:
ejercicios
2,
3,
10,
13,
14,
17,
24,
30,
35
y
36.
3.1. Se
tienen
dos
muelles
de
constantes
elásticas
𝑘!
y
𝑘!
en
cuyos
extremos
se
disponen
dos
masas
𝑚!
y
𝑚!
respectivamente,
tal
que
𝑚! < 𝑚!.
Al
oscilar,
las
fuerzas
que
actúan
sobre
cada
una
de
estas
masas
en
función
de
la
elongación
aparecen
representadas
en
la
figura:
a) ¿Cuál
es
el
muelle
de
mayor
constante
elástica?
b) ¿Cuál
de
estas
dos
masas
tendrá
mayor
periodo
de
oscilación?
Sol:
a)
𝒌 𝟏 > 𝒌 𝟐;
b)
𝑻 𝟏 < 𝑻 𝟐
3.2. Se
dispone
de
un
muelle
elástico
sujeto
por
un
extremo
al
techo
de
la
habitación.
Si
colgamos
por
el
otro
extremo
un
cuerpo
de
6
kg
de
masa,
el
muelle
se
alarga
20
cm.
Calcule:
a) La
constante
elástica
del
muelle:
b) El
periodo
de
las
oscilaciones
que
realizará
si
se
le
aparta
de
su
posición
de
equilibrio
y
se
le
deja
libremente
para
que
realice
un
MAS.
a) Determinaremos
la
constante
de
elasticidad
por
medio
de
la
ley
de
Hooke,
ya
que
en
equilibrio,
el
peso
del
objeto
que
deforma
el
muelle,
y
la
fuerza
recuperadora
del
mismo
tienen
el
mismo
módulo
y
sentidos
opuestos:
𝑃 = 𝐹 → 𝑚𝑔 = 𝑘𝑥 → 𝑘 =
𝑚𝑔
𝑥
→ 𝑘 =
6 𝑘𝑔 · 9!8𝑚/𝑠!
0!2 𝑚
→ 𝒌 = 𝟐𝟗𝟒 𝑵/𝒎
b) Aunque
la
constante
de
elasticidad
estática
y
dinámica
no
son
exactamente
iguales,
utilizaremos
el
dato
calculado
en
el
apartado
anterior
para
obtener
el
periodo
de
la
oscilación:
𝑇 =
1
𝑓
=
2𝜋
𝜔
=
2𝜋
𝑘/𝑚
= 2𝜋
𝑚
𝑘
= 2𝜋
6 𝑘𝑔
294 𝑁/𝑚
→ 𝑻 = 𝟎!
𝟗 𝒔
TIPO
16
LIBRO
PÁGINAS
26,
27
y
28:
ejercicios
5,
26
y
37.
3.3. Escribe
la
ecuación
senoidal
del
movimiento
del
movimiento
del
muelle
de
la
figura
cuya
gráfica
posición
–
tiempo
es:
Sol:
𝐱 𝐭 = 𝟎!
𝟏 · 𝐬𝐞𝐧 𝛑𝐭 +
𝝅
𝟔
𝐦

2.
Colegio Ntra. Sra. de la Fuencisla · Segovia
Camino
de
la
Piedad,
8
-­‐
C.P.
40002
-­‐
Segovia
-­‐
Tlfns.
921
43
67
61
-­‐
Fax:
921
44
34
47
www.maristassegovia.org
|
fuencisla@maristascompostela.org
3.4. El
bloque
de
la
figura,
de
masa
M
=
0,5
kg,
está
apoyado
sobre
una
superficie
horizontal
sin
rozamiento
y
unido
a
una
pared
mediante
un
resorte
de
masa
despreciable
y
constante
recuperadora
K
=
8
N/m.
Inicialmente
se
hace
actuar
sobre
M
una
fuerza
F
=
2
N
en
el
sentido
indicado.
A
continuación,
una
vez
que
M
ha
alcanzado
el
equilibrio,
se
anula
F.
¿Con
qué
amplitud
oscilará
M?
¿Con
qué
frecuencia
angular,
𝜔?
3.5. De
un
resorte
elástico
colgamos
una
masa
puntual
de
5
kg
y
éste
se
estira
9’8
cm
hasta
alcanzar
el
nuevo
equilibrio.
Desde
esta
posición
se
desplaza
la
masa
10
cm,
dejándola
oscilar
libremente
a
continuación.
Calcular:
a) El
valor
de
la
constante
elástica.
b) La
ecuación
del
movimiento
armónico
simple
que
describe
la
masa
puntual.
a) Aplicamos
la
ley
de
Hook
para
calcular
el
valor
de
la
constante
elástica
del
muelle:
𝐹 = 𝑘𝑦!
Como
el
sistema
está
en
equilibrio
la
resultante
de
las
fuerzas
debe
ser
nula,
es
decir,
el
peso
debe
ser
igual
a
la
fuerza
recuperadora
en
módulo
y
dirección,
pero
de
sentido
contrario:
𝑃 = 𝐹 → 𝑚𝑔 = 𝑘𝑦! → 𝑘 =
𝑚𝑔
𝑦!
𝒌 =
5𝑘𝑔 · 9!8 𝑚/𝑠!
0!098 𝑚
= 𝟓𝟎𝟎 𝑵/𝒎
b) Sabemos
que
la
ecuación
que
describe
un
movimiento
armónico
simple
es:
𝑦 𝑡 = 𝐴 · sin 𝜔𝑡 + 𝜑!
Calculamos
las
constantes.
Dado
que
nos
dicen
que
se
deja
oscilar
libremente
la
masa
desde
10
cm,
ese
será
el
valor
de
la
amplitud
𝐴 = 0!
1 𝑚.
Podemos
hallar
el
valor
de
la
pulsación
del
movimiento
a
partir
de
la
masa
y
la
constante
recuperadora
del
muelle:
𝜔 =
𝑘
𝑚
=
500 𝑁/𝑚
5 𝑘𝑔
→ 𝜔 = 10 𝑟𝑎𝑑/𝑠
Por
último,
para
calcular
el
valor
del
desfase
inicial
aplicamos
las
condiciones
iniciales:
𝑦 0 𝑠 = 0!
1𝑚 = 0!
1𝑚 · sin 0 + 𝜑!
Esta
ecuación
solo
se
cumplirá
para
aquellos
valores
que
cumplan
que
sin 𝜑! = 1.
Es
decir:
𝜑! =
𝜋
2
+ 2𝑛𝜋 𝑟𝑎𝑑; ∀ 𝑛 ∈ ℕ
Ya
que
todas
las
soluciones
tienen
el
mismo
significado
físico
vamos
a
quedarnos
con
𝜑! =
!
!
𝑟𝑎𝑑.
Una
vez
calculadas
todas
las
constantes
del
movimiento,
la
ecuación
del
movimiento
armónico
simple
será:
𝒚 𝒕 = 𝟎!
𝟏 𝒎 · 𝐬𝐢𝐧 𝟏𝟎𝒕 +
𝝅
𝟐

3.
Colegio Ntra. Sra. de la Fuencisla · Segovia
Camino
de
la
Piedad,
8
-­‐
C.P.
40002
-­‐
Segovia
-­‐
Tlfns.
921
43
67
61
-­‐
Fax:
921
44
34
47
www.maristassegovia.org
|
fuencisla@maristascompostela.org
TIPO
17
LIBRO
PÁGINAS
26,
27
y
28:
ejercicios
1,
18,
19,
21
y
34.
3.6. Una
masa
de
20
g
realiza
un
movimiento
armónico
en
el
extremo
de
un
resorte
que
da
dos
oscilaciones
por
segundo,
siendo
la
amplitud
del
mismo
5
cm.
Calcula:
a) La
velocidad
máxima
de
la
masa
que
oscila.
b) La
aceleración
de
la
masa
en
el
extremo
de
su
movimiento.
c) La
constante
k
del
resorte.
Sol:
a)
𝒗 𝒎𝒂𝒙 = 𝟎!
𝟐 𝝅 𝒎/𝒔;
b)
𝒂 = 𝟎!
𝟖 𝝅 𝟐
𝒎/𝒔 𝟐
;
c)
𝒌 = 𝟎!
𝟑𝟐 𝝅 𝟐
𝑵/𝒎
3.7. En
el
extremo
de
un
muelle
colocamos
un
cuerpo,
lo
estiramos
4
cm
y
lo
dejamos
oscilar
libremente.
Escribe
la
función
que
nos
permite
conocer
su
elongación,
velocidad
y
aceleración
en
función
del
tiempo
si
vibra
con
una
frecuencia
de
2
Hz.
Representa
gráficamente
dichas
funciones
tomando
valores
del
tiempo
que
permitan
conocer
lo
que
sucede
en
dos
oscilaciones
completas.
Sol:
𝒙 𝒕 = 𝟎!
𝟎𝟒 · 𝐜𝐨𝐬 𝟒𝝅 · 𝒕 𝒎;
𝒗 𝒕 = −𝟎!
𝟏𝟔𝝅 · 𝐜𝐨𝐬 𝟒𝝅 · 𝒕 𝒎/𝒔;
𝒂 𝒕 = −𝟎!
𝟔𝟒𝝅 𝟐
· 𝐜𝐨𝐬 𝟒𝝅 · 𝒕 𝒎/𝒔 𝟐
3.8. Un
punto
material
está
animado
de
un
movimiento
armónico
simple
a
lo
largo
del
eje
X,
alrededor
de
su
posición
de
equilibrio
en
x
=
0.
En
el
instante
t
=
0,
el
punto
material
está
situado
en
x
=
0
y
se
desplaza
en
el
sentido
negativo
del
eje
X
con
una
velocidad
de
40
cm·∙s-­‐1
.
La
frecuencia
del
movimiento
es
de
5
Hz.
a) Determina
la
posición
en
función
del
tiempo.
b) Calcula
la
posición
y
la
velocidad
en
el
instante
t
=
5
s.
Sol:
a)
𝒙 𝒕 = 𝟎!
𝟎𝟏𝟑 · 𝐬𝐢𝐧 𝟏𝟎𝝅 · 𝒕 + 𝝅 𝒎;
b)
𝒙 𝟓 𝒔 = 𝟎 𝒎, 𝒗 𝟓 𝒔 = −𝟎!
𝟒 𝒎/𝒔
3.9. Una
pequeña
plataforma
horizontal
sufre
un
movimiento
armónico
simple
en
sentido
vertical,
de
3
cm
de
amplitud
y
cuya
frecuencia
aumenta
progresivamente.
Sobre
ella
reposa
un
pequeño
objeto.
a) ¿Para
qué
frecuencia
dejará
el
objeto
de
estar
en
contacto
con
la
plataforma?
b) ¿Cuál
será
la
velocidad
de
la
plataforma
en
ese
instante?
a) El
objeto
dejará
de
estar
en
contacto
con
la
plataforma
cuando
la
aceleración
con
la
que
descienda
la
plataforma
sea
mayor
que
la
aceleración
de
la
gravedad
que
es
valor
máximo
con
que
puede
caer
el
objeto.
El
valor
máximo
de
la
aceleración
se
adquiere
en
el
extremo
superior
del
recorrido
de
la
plataforma:
𝑔 = 𝑎!"#
La
aceleración
se
calcula
como
la
segunda
derivada
de
la
elongación
respecto
del
tiempo:
𝑎 𝑡 =
𝑑! 𝑦 𝑡
𝑑𝑡!
= −𝜔!
𝐴 · sin 𝜔𝑡 + 𝜑!
Como
queremos
que
la
aceleración
sea
máxima,
el
seno
tendrá
que
tomar
su
valor
máximo:
𝑎!"# = 𝜔!
𝐴 ⟶ 𝜔 =
𝑎!"#
𝐴
=
𝑔
𝐴
⟶ 𝑓 =
1
2𝜋
𝑔
𝐴
Sustituyendo
valores:
𝒇 =
1
2𝜋
·
9!8 𝑚/𝑠!
0!03 𝑚
= 𝟐′𝟖𝟖 𝑯𝒛

4.
Colegio Ntra. Sra. de la Fuencisla · Segovia
Camino
de
la
Piedad,
8
-­‐
C.P.
40002
-­‐
Segovia
-­‐
Tlfns.
921
43
67
61
-­‐
Fax:
921
44
34
47
www.maristassegovia.org
|
fuencisla@maristascompostela.org
b) La
plataforma
se
encuentra
en
el
extremo
superior
del
recorrido
por
lo
que
la
velocidad
será
nula:
𝑣 𝑡 =
!" !
!"
= 𝜔𝐴 · cos 𝜔𝑡 + 𝜑!
cos 𝜔𝑡 + 𝜑!
cos 𝜔𝑡 + 𝜑! = 1 − sin! 𝜔𝑡 + 𝜑! = 1 −
!! !
!
sin!
𝛼 + cos!
𝛼 = 1
sin(𝜔𝑡 + 𝜑!) = 𝑦 𝑡 /𝐴
𝑣 𝑡 = 𝜔𝐴 · 1 −
!! !
!
= 𝜔 𝐴! − 𝑦! 𝑡
Como
en
nuestro
caso
el
objeto
deja
de
estar
en
contacto
con
la
plataforma
cuando
𝑦 𝑡 = 𝐴:
𝒗 𝒕 = 𝟎 𝒎/𝒔
3.10. La
ecuación
de
una
onda
armónica
transversal
que
se
propaga
por
una
cuerda,
expresada
en
unidades
del
S.I.
es:
𝐲 𝐱, 𝐭 = 𝟎!
𝟎𝟑 · 𝐬𝐢𝐧 𝟐𝐭 + 𝟏𝟎𝐱 .
Determina:
a) La
frecuencia,
la
longitud
de
onda
y
la
velocidad
de
propagación
de
dicha
onda.
b) La
velocidad
de
vibración,
tras
5
segundos,
de
un
punto
situado
a
una
distancia
del
origen
de
15
cm.
c) La
diferencia
de
fase
entre
dos
puntos
de
la
cuerda
separados
una
distancia
de
20
cm.
a) Por
comparación
con
la
expresión
general
de
una
onda
armónica
𝑦 𝑥, 𝑡 = 𝐴 · sin 𝜔𝑡 − 𝜅𝑥
podemos
obtener
varias
magnitudes:
𝐴 = 0!
03 𝑚 𝜔 = 2 𝑟𝑎𝑑/𝑠 𝜅 = 10 𝑟𝑎𝑑/𝑚
A
partir
de
estas
magnitudes
podemos
obtener
la
frecuencia:
𝛎 =
𝜔
2𝜋
=
2 𝑟𝑎𝑑/𝑠
2𝜋 𝑟𝑎𝑑
= 𝛑!𝟏
𝐇𝐳
La
longitud
de
onda:
𝛌 =
2𝜋
𝜅
=
2𝜋 𝑟𝑎𝑑
10 𝑟𝑎𝑑/𝑚
=
𝛑
𝟓
𝐦
Y
la
velocidad
de
propagación:
(en
este
caso
la
propagación
de
la
onda
se
produce
en
sentido
negativo
del
eje
x).
𝐯 𝐏 =
𝜆
𝑇
= 𝜆 · 𝜈 =
𝜋
5
𝑚 · 𝜋!!
𝑠!!
= 𝟎!
𝟐 𝐦/𝐬
b) La
velocidad
de
vibración
se
calcula
derivando
la
elongación
respecto
del
tiempo:
𝑣 =
𝑑𝑦
𝑑𝑡
= 0!
06 · cos 2𝑡 + 10𝑥
En
𝑡 = 5 𝑠
y
𝑥 = 0!
15 𝑚:
𝐯 = 0!
06 · cos 2 · 5 + 10 · 0′15 = 0!
06 · cos 11′5 = 0!
06 · 0!
98 𝑚/𝑠 = 𝟎!
𝟎𝟐𝟗 𝐦/𝐬
c) Nos
piden
calcular
el
desfase
entre
dos
puntos
separados
0’2
m
pero
en
el
mismo
instante
de
tiempo
⟹ Δ𝑡 = 0 𝑠:
Δ𝜑 = 𝜑! − 𝜑! = 𝜔𝑡! + 𝜅𝑥! − 𝜔𝑡! + 𝜅𝑥! = 𝜔𝑡! − 𝜔𝑡! + 𝜅𝑥! − 𝜅𝑥!
Δ𝜑 = 𝜔 𝑡! − 𝑡! + 𝜅 𝑥! − 𝑥! = 𝜔 · Δ𝑡 + 𝜅 · Δx = κ · Δx
𝚫𝝋 = 𝟏𝟎 𝒓𝒂𝒅/𝒎 · 𝟎!
𝟐 𝒎 = 𝟐 𝒓𝒂𝒅

5.
Colegio Ntra. Sra. de la Fuencisla · Segovia
Camino
de
la
Piedad,
8
-­‐
C.P.
40002
-­‐
Segovia
-­‐
Tlfns.
921
43
67
61
-­‐
Fax:
921
44
34
47
www.maristassegovia.org
|
fuencisla@maristascompostela.org
TIPO
18
LIBRO
PÁGINAS
26,
27
y
28:
ejercicios
6,
8,
11,
12,
20,
22,
25,
27,
29,
31
y
38.
3.11. Una
partícula
de
masa
𝑚 = 0!
1 𝑘𝑔
oscila
armónicamente
en
la
forma
𝑥 = 𝐴 · sin 𝜔𝑡,
con
amplitud
𝐴 = 0!
2 𝑚
y
frecuencia
angular
𝜔 = 2𝜋 𝑟𝑎𝑑/𝑠.
a) Calcula
la
energía
mecánica
de
la
partícula.
b) Determina
y
representa
gráficamente
(en
la
misma
gráfica)
las
energías
potencial
y
cinética
de
la
masa
en
función
del
tiempo
para
4
periodos
completos.
Sol:
a)
𝐄 𝐌 = 𝟕!
𝟗 · 𝟏𝟎!𝟐
𝐉,
b)
𝐄 𝐏 = 𝟎!
𝟎𝟕𝟗 · 𝐬𝐢𝐧 𝟐𝝅𝒕 𝟐
𝐉; 𝐄 𝐂 = 𝟎!
𝟎𝟕𝟗 · 𝐜𝐨𝐬 𝟐𝝅𝒕 𝟐
𝐉
3.12. Una
partícula
de
0’5
kg
que
describe
un
movimiento
armónico
simple
de
frecuencia
5/π
Hz
tiene,
inicialmente,
una
energía
cinética
de
0’2
J
y
una
energía
potencial
de
0’8
J.
a) Calcula
la
posición,
velocidad
y
desfase
iniciales,
así
como
la
amplitud
de
la
oscilación
y
la
velocidad
máxima.
b) Haz
un
análisis
de
las
transformaciones
de
energía
que
tienen
lugar
en
un
ciclo
completo.
¿Cuál
será
el
desplazamiento
en
el
instante
en
el
que
las
energías
cinética
y
potencial
son
iguales?
Sol:
a)
𝒙 𝒐 = 𝟎!
𝟏𝟖 𝒎, 𝑨 = 𝟎!
𝟐 𝒎, 𝝋 𝒐 = 𝟏!
𝟏𝟐 𝒓𝒂𝒅, 𝒗 𝒐 = 𝟎!
𝟖𝟕 𝒎/𝒔, 𝒗 𝒎𝒂𝒙 = 𝟐 𝒎/𝒔
b)
𝒙!
= 𝟎!
𝟏𝟒 + 𝒏𝝅 𝒎 ∀ 𝒏 = 𝟎, 𝟏, 𝟐 …
3.13. Una
masa
m
que
describe
un
movimiento
armónico
simple,
tarda
1
s
en
desplazarse
desde
un
extremo
de
la
trayectoria
al
otro
extremo.
La
distancia
entre
ambos
extremos
es
de
5
cm.
Determina:
a) El
periodo
del
movimiento.
b) La
energía
cinética
de
la
partícula
en
t
=
2’75
s,
sabiendo
que
en
t
=
0
su
elongación
es
nula.
c) El
primer
instante
en
el
que
las
energías
cinética
y
potencial
del
sistema
coinciden.
Sol:
a)
𝑻 = 𝟐 𝒔;
b)
𝑬 𝑪 = 𝒎 · 𝟏!
𝟓𝟒 · 𝟏𝟎!𝟑
𝑱;
c)
𝒕 = 𝟎!
𝟐𝟔 𝒔
3.14. Un
bloque
de
50
g,
conectado
a
un
muelle
de
constante
elástica
35
N/m,
oscila
en
una
superficie
horizontal
sin
rozamiento
con
una
amplitud
de
4
cm.
Cuando
el
bloque
se
encuentra
a
1
cm
de
su
posición
de
equilibrio,
calcula:
a) La
fuerza
ejercida
sobre
el
bloque.
b) La
aceleración
del
bloque.
c) La
energía
potencial
elástica
del
sistema.
d) La
velocidad
del
bloque.
Sol:
a)
F
=
35
N,
b)
a
=
7m/s2
,
c)
EP
=
1’75·∙10-­‐3
J,
d)
v
=
1’02
m/s
3.15. Cierto
muelle,
que
se
deforma
20
cm
cuando
se
le
cuelga
una
masa
de
1’0
kg,
se
coloca
sin
deformación
unido
a
la
misma
masa
sobre
una
superficie
sin
rozamiento,
como
se
indica
en
la
figura.
En
esta
posición,
se
tira
de
la
masa
hasta
que
el
muelle
se
alarga
2’0
cm
y,
posteriormente,
se
suelta.
Despreciando
la
masa
del
muelle,
calcula:
a) La
ecuación
de
la
posición
para
el
movimiento
armónico
simple
resultante.
b) Las
energías
cinética,
potencial
elástica
y
mecánica
total
cuando
ha
trascurrido
un
tiempo
t
=
(3/4)·∙T,
donde
T
es
el
periodo
del
m.v.a.s.
Sol:
a)
𝒙 𝒕 = 𝟎!
𝟐 · 𝐬𝐢𝐧 𝟕𝒕 +
𝝅
𝟐
𝒎;
b)
𝑬 𝑷 = 𝟎 𝑱, 𝑬 𝑪 = 𝑬 𝑴 = 𝟎!
𝟗𝟖 𝑱

6.
Colegio Ntra. Sra. de la Fuencisla · Segovia
Camino
de
la
Piedad,
8
-­‐
C.P.
40002
-­‐
Segovia
-­‐
Tlfns.
921
43
67
61
-­‐
Fax:
921
44
34
47
www.maristassegovia.org
|
fuencisla@maristascompostela.org
3.16. Una
partícula
de
10
g
de
masa
oscila
armónicamente
según
la
expresión
x
=A·∙sin(ωt).
En
la
figura
se
representa
la
velocidad
de
esta
partícula
en
función
del
tiempo.
Calcula:
a) La
frecuencia
angular,
ω,
y
la
amplitud,
A,
de
la
oscilación.
b) La
energía
cinética
de
la
partícula
en
el
instante
t1
=
0’5
s,
y
la
energía
potencial
en
t2
=
0’75
s.
c) ¿Qué
valores
tienen
las
dos
energías
anteriores?
¿Por
qué?
Sol:
a)
𝝎 = 𝟐𝝅 𝒓𝒂𝒅/𝒔, 𝑨 = 𝝅!𝟏
𝒎;
b)
𝑬 𝑪 = 𝟎!
𝟎𝟐 𝑱, 𝑬 𝑷 = 𝟎!
𝟎𝟐 𝑱
3.17. Una
masa
de
2
kg
está
unida
a
un
muelle
horizontal
cuya
constante
recuperadora
es
k
=
10
N/m.
El
muelle
se
comprime
5
cm
desde
la
posición
de
equilibrio
(x
=
0)
y
se
deja
en
libertad.
Determinar:
a) La
expresión
de
la
posición
de
la
masa
en
función
del
tiempo.
b) Los
módulos
de
la
velocidad
y
de
la
aceleración
de
la
masa
en
un
punto
situado
a
2
cm
de
la
posición
de
equilibrio.
c) La
fuerza
recuperadora
cuando
la
masa
se
encuentra
en
los
extremos
de
la
trayectoria.
d) La
energía
mecánica
del
sistema
oscilante.
Sol:
a)
𝒙 𝒕 = 𝟎!
𝟎𝟓 · 𝐬𝐢𝐧 𝟓 𝒕 −
𝝅
𝟐
𝒎;
b)
𝒗 = 𝟎!
𝟏 𝒎/𝒔, 𝒂 = −𝟎!
𝟏 𝒎/𝒔 𝟐
;
c)
𝑭 = −𝟎!
𝟓 𝑵
d)
𝑬 𝑴 = 𝟎!
𝟎𝟏𝟐𝟓 𝑱
3.18. En
la
figura
se
muestra
la
representación
gráfica
de
la
energía
potencial
(Ep)
de
un
oscilador
armónico
simple
constituido
por
una
masa
puntual
de
valor
200
g
unida
a
un
muelle
horizontal,
en
función
de
su
elongación
(x).
a) Calcula
la
constante
elástica
del
muelle.
b) Calcula
la
aceleración
máxima
del
oscilador.
c) Determina
la
energía
cinética
cuando
la
masa
está
en
la
posición:
x
=
+2,3
cm.
d) ¿Dónde
se
encuentra
la
masa
puntual
cuando
el
módulo
de
su
velocidad
es
igual
a
la
cuarta
parte
de
su
velocidad
máxima?
Sol:
𝒂) 𝒌 = 𝟖𝟎 𝑵/𝒎, 𝒃) 𝒂 = 𝟐𝟎 𝒎/𝒔 𝟐
, 𝒄) 𝑬 𝑪 = 𝟕′𝟖𝟖 · 𝟏𝟎!𝟐
𝑱, 𝒅) 𝒙 = ± 𝟒′𝟖𝟒 · 𝟏𝟎!𝟐
𝒎
3.19. Las
líneas
siguientes
representan
la
elongación
frente
al
tiempo
para
dos
móviles
con
MAS.
Obsérvalas
y
responde:
a) ¿Cuál
de
los
dos
móviles
tarda
más
en
dar
una
oscilación
completa?
b) ¿Cuál
de
los
dos
móviles
tiene
mayor
energía
mecánica?
c) Suponiendo
que
los
dos
móviles
tienen
la
misma
masa,
¿cuál
de
ellos
se
ve
sometido
a
una
mayor
fuerza
de
recuperación?

7.
Colegio Ntra. Sra. de la Fuencisla · Segovia
Camino
de
la
Piedad,
8
-­‐
C.P.
40002
-­‐
Segovia
-­‐
Tlfns.
921
43
67
61
-­‐
Fax:
921
44
34
47
www.maristassegovia.org
|
fuencisla@maristascompostela.org
3.20. Las
líneas
siguientes
representan
la
elongación
frente
al
tiempo
para
dos
móviles
con
MAS.
Obsérvalas
y
responde:
a) ¿Cuál
de
los
dos
móviles
tarda
más
en
dar
una
oscilación
completa?
b) ¿Cuál
de
los
dos
móviles
tiene
mayor
energía
mecánica?
c) Suponiendo
que
los
dos
móviles
tienen
la
misma
masa,
¿cuál
de
ellos
se
ve
sometido
a
una
mayor
fuerza
de
recuperación?
3.21. Una
partícula
de
masa
m
está
animada
de
un
movimiento
armónico
simple
de
amplitud
A
y
frecuencia
f.
a) Deduzca
las
expresiones
de
las
energías
cinética
y
potencial
de
la
partícula
en
función
del
tiempo.
b) Deduzca
la
expresión
de
la
energía
mecánica
de
la
partícula.
a) Calculamos
primero
la
energía
cinética
sustituyendo
la
velocidad
de
vibración
en
la
ecuación:
𝐸! =
1
2
𝑚𝑣!
=
1
2
𝑚 𝐴𝜔 cos 𝜔𝑡 + 𝜑!
!
=
1
2
𝑚𝐴!
𝜔!
cos!
𝜔𝑡 + 𝜑! =
=
1
2
𝑚𝐴!
𝑘
𝑚
cos!
𝜔𝑡 + 𝜑! =
1
2
𝑘𝐴!
1 − sin!
𝜔𝑡 + 𝜑! =
1
2
𝑘 𝐴!
− 𝐴!
𝑠𝑖𝑛!
𝜔𝑡 + 𝜑!
𝐸! =
1
2
𝑘𝐴!
1 − 𝑠𝑖𝑛!
𝜔𝑡 + 𝜑!
Ahora
podemos
calcular
la
energía
potencial
porque
las
fuerzas
elásticas
son
fuerzas
conservativas:
𝑊 = −∆𝐸! = 𝐸!!
− 𝐸!!
=
1
2
𝑘𝑥!
!
−
1
2
𝑘𝑥!
!
Consideramos
EP
=
0
cuando
x
=
0;
es
decir,
en
la
posición
de
equilibrio:
𝐸! =
1
2
𝑘𝑥!
=
1
2
𝑘 𝐴!
𝑠𝑖𝑛!
𝜔𝑡 + 𝜑!
Ya
tenemos
las
expresiones
de
las
energías
potencial
y
cinética
del
movimiento
armónico
simple
en
función
de
t,
sólo
nos
falta
calcular
el
valor
de
k:
𝜅
𝑚
= 𝜔 → 𝑘 = 𝑚𝜔!
= 𝑚 2𝜋 · 𝑓 !
= 4𝑚𝜋!
𝑓!
Entonces
la
solución
será:
𝑬 𝑪 = 𝟐𝒎𝝅 𝟐
𝒇 𝟐
𝑨 𝟐
𝟏 − 𝒔𝒊𝒏 𝟐
𝟐𝝅𝒇 · 𝒕 + 𝝋 𝟎
𝑬 𝑷 = 𝟐𝒎𝝅 𝟐
𝒇 𝟐
𝑨 𝟐
𝒔𝒊𝒏 𝟐
𝟐𝝅𝒇 · 𝒕 + 𝝋 𝟎
b) Sabemos
que
la
energía
mecánica
es
constante
en
el
tiempo
y
se
calcula
sumando
la
energía
cinética
y
potencial:
𝐸! = 𝐸! + 𝐸! = 2𝑚𝜋!
𝑓!
𝐴!
1 − 𝑠𝑖𝑛!
2𝜋𝑓 · 𝑡 + 𝜑! + 2𝑚𝜋!
𝑓!
𝐴!
𝑠𝑖𝑛!
2𝜋𝑓 · 𝑡 + 𝜑!
𝑬 𝑴 = 𝟐𝒎𝝅 𝟐
𝒇 𝟐
𝑨 𝟐

8.
Colegio Ntra. Sra. de la Fuencisla · Segovia
Camino
de
la
Piedad,
8
-­‐
C.P.
40002
-­‐
Segovia
-­‐
Tlfns.
921
43
67
61
-­‐
Fax:
921
44
34
47
www.maristassegovia.org
|
fuencisla@maristascompostela.org
TIPO
19
LIBRO
PÁGINA
99:
ejercicio
23.
LIBRO
PÁGINAS
26
y
27:
ejercicios
7,
9,
15,
16
y
28.
3.22. Un
péndulo
simple
oscila
con
una
elongación
máxima
de
18o
,
desarrollando
10
oscilaciones
por
segundo.
Tomando
como
instante
inicial
la
posición
de
equilibrio:
a) Escribe
su
elongación
en
función
del
tiempo.
b) Determina
su
periodo
de
oscilación
en
la
Luna,
donde
la
gravedad
es,
aproximadamente
un
sexto
de
la
terrestre.
Sol:
a)
𝜽 𝒕 = 𝟏𝟖° · 𝐬𝐢𝐧 𝟐𝟎 𝝅 · 𝒕 ;
b)
𝑻!
= 𝟎!
𝟐𝟒 𝒔
3.23. Un
péndulo
simple
está
construido
con
una
bolita
suspendida
de
un
hilo
de
longitud
L
=
2
m.
Para
pequeñas
oscilaciones,
su
periodo
de
oscilación
en
un
cierto
lugar
resulta
ser
T
=
2’84
s.
a) Determina
la
intensidad
del
campo
gravitatorio
en
el
lugar
donde
se
ha
medido
el
periodo.
b) Considera
que
el
movimiento
de
la
bolita
es
prácticamente
paralelo
al
suelo.
Sabiendo
que
la
velocidad
máxima
de
la
bolita
es
de
0’4
m/s,
calcula
la
amplitud
de
su
oscilación
y
representa
gráficamente
su
posición
en
función
del
tiempo,
x(t).
Toma
origen
para
el
tiempo,
t
=
0,
en
un
extremos
de
la
oscilación.
Sol:
a)
𝒈 = 𝟗!
𝟕𝟗 𝑵/𝒎;
b)
𝑨 = 𝟎!
𝟏𝟖 𝒎
3.24. Un
péndulo
simple
que
realiza
pequeñas
oscilaciones
tiene
un
periodo
de
2,000
s
cuando
está
situado
en
un
punto
al
nivel
del
mar.
Cuando
lo
situamos
en
lo
alto
de
una
montaña
su
periodo
es
2,002
s.
Calcula
la
altura
de
la
montaña.
Sabemos
que
el
periodo
de
un
péndulo
es:
𝑇 = 2𝜋
𝐿
𝑔
Es
decir,
sólo
depende
de
dos
variables
(la
longitud
del
hilo
y
la
gravedad).
Como
no
cambiamos
de
péndulo,
la
única
variable
que
va
a
cambiar
va
a
ser
la
gravedad.
Por
lo
tanto,
podemos
calcular
la
diferencia
de
gravedad
entre
la
montaña
y
el
nivel
del
mar
con
la
diferencia
de
periodos,
para
ello,
primero
despejamos
g:
𝑇!
= 4𝜋!
𝐿
𝑔
⟹ 𝑔 =
4𝜋! 𝐿
𝑇!
Ahora,
sabemos
que:
𝑔! ⟶ 𝑇! = 2!
000 𝑠
𝑔! ⟶ 𝑇! = 2!
002 𝑠
Calculamos
la
relación
entre
ambas
gravedades:
𝑔!
𝑔!
=
4𝜋!
𝐿
𝑇!
!
4𝜋! 𝐿
𝑇!
!
=
𝑇!
!
𝑇!
! =
2!000 𝑠 !
2!002 𝑠 !
= 0′998

9.
Colegio Ntra. Sra. de la Fuencisla · Segovia
Camino
de
la
Piedad,
8
-­‐
C.P.
40002
-­‐
Segovia
-­‐
Tlfns.
921
43
67
61
-­‐
Fax:
921
44
34
47
www.maristassegovia.org
|
fuencisla@maristascompostela.org
Una
vez
que
conocemos
la
relación
entre
las
intensidades
de
campo
podemos
calcular
la
altura:
𝑔! = 𝑔! ·
𝑅!
!
𝑅! + ℎ !
𝑔!
𝑔!
=
𝑅!
!
𝑅! + ℎ !
= 0′998
𝑅!
!
= 0!
998 · 𝑅! + ℎ !
𝑅!
!
= 0!
998 · 𝑅!
!
+ ℎ!
+ 2𝑅!ℎ
𝑅!
!
= 0!
998 · 𝑅!
!
+ 0!
998 · ℎ!
+ 1′996𝑅!ℎ
0!
998 · ℎ!
+ 1!
996𝑅! · ℎ − 0!
002𝑅!
!
= 0
Sustituimos
el
valor
de
𝑅!
y
despejamos
h:
0!
998 · ℎ!
+ 12714520 · ℎ − 81153800000 = 0
ℎ! = −12746380 𝑚
esta
solución
no
es
válida,
ya
que
la
altura
debe
ser
un
valor
positivo.
ℎ! = 6380 𝑚
Por
lo
tanto
la
montaña
tiene
una
altura
de
𝟔 𝟑𝟖𝟎 𝒎.