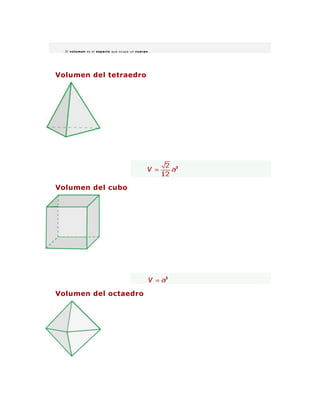
1. El volumen es el espacio que ocupa un cuerpo.
Volumen del tetraedro
Volumen del cubo
Volumen del octaedro

2. Volumen del dodecaedro
Volumen del icosaedro

3. Volumen del prisma
Volumen del ortoedro
Volumen de la pirámide

4. Volumen del tronco de pirámide
Volumen del cilindro

5. Volumen del cono
Volumen del tronco de cono

6. Volumen de la esfera
Volumen de la semiesfera
Volumen de la cuña esférica

7. Volumen del casquete esférico
Volumen de la zona esférica

8. Área del cono
Ejercicios
Para una fiesta, Luís ha hecho 10 gorros de forma cónica
con cartón. ¿Cuánto cartón habrá utilizado si las dimensiones
del gorro son 15 cm de radio y 25 cm de generatriz?

9. Calcula el área lateral y total de un
cono cuya generatriz mide 13 cm y el radio de la base es de 5
cm.
Calcula el área lateral y total de un
cono cuya altura mide 4 cm y el radio de la base es de 3 cm.

11. Volumen
El volumen es el espacio que ocupa un cuerpo.
Volumen del tetraedro
Volumen del cubo
Volumen del octaedro

12. Volumen del dodecaedro
Volumen del icosaedro

13. Volumen del prisma
Volumen del ortoedro
Volumen de la pirámide

14. Volumen del tronco de pirámide
Volumen del cilindro

15. Volumen del cono
Volumen del tronco de cono

16. Volumen de la esfera

17. Volumen de la semiesfera
Volumen de la cuña esférica

18. Volumen del casquete esférico
Volumen de la zona esférica

19. Perímetro
El perímetro de una figura geométrica plana es igual a
la suma de laslongitudes de sus lados.
Perímetro de un triangulo
Triángulo
Equilátero
Triángulo
Isósceles
Triángulo
Escaleno
Perímetro de un cuadrado
Perímetro de un rectángulo

20. Perímetro de un rombo
Perímetro del romboide
P = 2 · (a + b)
Perímetro de un pentágono regular

21. Perímetro de un hexágono regular
Perímetro de un polígono regular
n = número de lados
Longitud de una circunferencia

22. Ángulos
Un ángulo es la región del plano comprendida entre dos
semirrectas con origen común.
A las semirrectas se las llama lados del ángulo.
El origen común es el vértice.
Medida de ángulos
Para medir ángulos se utiliza el sistema sexagesimal.
Grado sexagesimal es la amplitud del ángulo
resultante de dividir la circunferencia en 360 partes
iguales.
1º = 60' = 3600''
1' = 60''

23. Radianes
Un radián (rad) es la medida del ángulo central de una
circunferencia cuya longitud de arco coincide con la longitud
de su radio.
1 rad= 57° 17' 44.8''
360º = 2 rad
180º = rad

24. Operaciones con ángulos
Suma de ángulos
La suma de dos ángulos es otro ángulo cuya amplitud es
la suma de las amplitudes de los dos ángulos iniciales.
Diferencia de ángulos
La resta de dos ángulos es otro ángulo cuya amplitud
es la diferencia entre la amplitud del ángulo mayor y la del
ángulo menor.

25. Producto de un número por un ángulo
El producto de un número por un ángulo es
otro ángulo cuya amplitud es la suma de tantos ángulos
iguales al dado como indique el número.
Cociente de un ángulo por un número
La división de un ángulo por un número es hallar
otro ángulo tal que multiplicado por ese número da como
resultado el ángulo original.
:4 =

26. Triángulo
Un triángulo es un polígono de tres lados.
Un triángulo está determinado por tres segmentos de
recta que se denominan lados, o portres puntos no alineados
llamados vértices.
Los vértices de
un triángulo se
escriben con
letras mayúsculas.
Los lados de
un triángulo se
escriben en minúscula,
con las mismas letras

27. de los vértices
opuestos.
Los ángulos de
un triángulo se
escriben igual que
los vértices.
Propiedades del triángulo
1 Un lado de un triángulo es menor que la suma de
los otros dos y mayor que sudiferencia.
a < b + c
a > b - c
2La suma de los ángulos interiores de un triángulo es
igual a 180°.
A + B + C =180º

28. 3 El valor de
un ángulo
exterior de
un triángulo es
igual a
la suma de
los dos
interiores no
adyacentes.
α = A + B
α = 180º - C
4En
un triángulo a m
ayor lado se
opone mayor
ángulo.

29. 5 Si un
triángulo
tiene dos lados
iguales,
sus ángulos
opuestos tambié
n son iguales.
Tipos de triángulos según sus lados
Triángulo equilátero
Tres lados iguales.

30. Triángulo isósceles
Dos lados iguales.
Triángulo escaleno
Tres lados desiguales.
Tipos de triángulos según sus ángulos
Triángulo acutángulo
Tres ángulos agudos

31. Triángulo rectángulo
Un ángulo recto
El lado mayor es la hipotenusa.
Los lados menores son los catetos.
Triángulo obtusángulo
Un ángulo obtuso.
Triángulos iguales
1Dos triángulos son iguales cuando tienen iguales un
lado y sus dos ángulos adyacentes.
2Dos triángulos son iguales cuando tienen dos lados
iguales y el ángulo comprendido.

32. 3Dos triángulos son iguales cuando tienen los tres lados
iguales.
Perímetro del triangulo
El perímetro del triangulo es igual a la suma de
las longitudes de sus tres lados.
Perímetro del triangulo equilátero
Perímetro del triangulo isósceles

33. Perímetro del triangulo escaleno
Área de un triángulo
El área de un triángulo es igual a base por altura
partido por 2.
La altura es la recta perpendicular trazada desde
un vértice al lado opuesto (o su prolongación).
Área de un triángulo equilátero

34. Área de un triángulo rectángulo
El área de un triángulo rectángulo es igual al producto
de los catetos partido por 2.
Semiperímetro
El semiperímetro de un triángulo es igual a la suma de
sus lados partido por 2.
Se nombra con la letra p.

35. Fórmula de Herón
La fórmula de Herón se utiliza para hallar el área de un
triángulo conociendo sus tres lados.
Circunferencia circunscrita a un triángulo
R
=
radio
de la
circu
nfere
ncia
circu

36. nscri
ta
Circunferencia inscrita en un triángulo
r = radio de la circunferencia inscrita
p = semiperímetro
Conociendo dos lados y el ángulo que forman

37. Área de un triángulo conociendo las
coordenadas de los vértices
El área de un triángulo es igual al la mitad del producto
escalar, en valor absoluto, del vector perpendicular a por el
vector .
Área de un triángulo por determinantes
Para resolver el determinante de orden tres utilizamos
la regla de Sarrus.El determinante está en valor absoluto

38. Los catetos son los lados opuestos a los ángulos
agudos de un triángulo rectángulo.
Los catetos son los lados menores del triángulo
rectángulo.
La hipotenusa es lado mayor del triángulo rectángulo.
Teorema del cateto
En un triángulo rectángulo un cateto es media
proporcional entre la hipotenusa y suproyección sobre ella.
a hipotenusa
b y c catetos
m proyección del cateto b sobre la hipotenusa
n proyección del cateto c sobre la hipotenusa

39. Ejemplos
La hipotenusa de un triángulo rectángulo mide 30 cm y la
proyección de un cateto sobre ella 10.8 cm. Hallar el otro
cateto.

40. La hipotenusa de un triángulo rectángulo mide 405.6 m y la
proyección de un cateto sobre ella 60 m. Calcular:
1 Los catetos.
2 La altura relativa a la hipotenusa.
3 El área del triángulo.

41. Teorema de Pitágoras
El cuadrado de la hipotenusa es igual a la suma de los
cuadrados de los catetos.
Ejemplos
La hipotenusa de un triángulo rectángulo mide 5 m y uno
de sus catetos 3 m. ¿Cuánto mide otro cateto?
Una escalera de 10 m de longitud está apoyada sobre la
pared. El pie de la escalera dista 6 m de la pared. ¿Qué altura
alcanza la escalera sobre la pared?

42. Teorema de la altura
En un triángulo rectángulo, la altura relativa a la
hipotenusa es media proporcionalentre los dos segmentos
que dividen a ésta.
a hipotenusa
b y c catetos
m proyección del cateto b sobre la hipotenusa
n proyección del cateto c sobre la hipotenusa

43. En un triángulo rectángulo, las proyecciones de los catetos
sobre la hipotenusa miden 4 y 9 metros. Calcular la altura
relativa a la hipotenusa.
Teorema del cateto
En un triángulo rectángulo un cateto es media
proporcional entre la hipotenusa y suproyección sobre ella.
a hipotenusa
b y c catetos
m proyección del cateto b sobre la hipotenusa
n proyección del cateto c sobre la hipotenusa

44. Ejemplo
La hipotenusa de un triángulo rectángulo mide 30 cm y la
proyección de un cateto sobre ella 10.8 cm. Hallar el otro
cateto.

45. Teorema de Thales
Si dos rectas cualesquieras se cortan por varias rectas
paralelas, los segmentos determinados en una de las
rectas son proporcionales a los segmentos
correspondientes en la otra.
Aplicaciones del teorema de Thales

46. El teorema de Thales se utiliza para dividir un
segmento en varias partes iguales.
Por ejemplo, dividir el segmento AB en 3 partes iguales
1. Se dibuja una semirrecta de origen el extremo A del segmento.
2. Tomando como unidad cualquier medida, se señalan en la
semirrecta 3 unidades de medida a partir de A.

47. 3. Por cada una de las divisiones de la semirrecta se trazan rectas
paralelas al segmento que une B con la última división sobre la
semirrecta. Los puntos obtenidos en el segmento AB determinan las
3 partes iguales en que se divide.
Ortocentro
El ortocentro es el punto de corte de las tres alturas.
Altura es cada una de las rectas perpendiculares trazadas desde
unvértice al lado opuesto (o su prolongación).
El ortocentro se expresa con la letra H.
Medianas de un triángulo
La Mediana es cada una de las rectas que une el punto
medio de un lado con el vértice opuesto.
El punto de corte de las tres medianas se
llama baricentro.

48. Ejercicio
Hallar las ecuaciones de las medianas y
el baricentro del triángulo de vértices: A(2, 0), B(0, 1) y C(-3,
-2).
Ecuación de la mediana que pasa por A y el punto medio
de BC
En primer lugar hallamos el punto medio de Bc

49. Calculamos la ecuación de la recta que pasa por dos
puntos.
Ecuación de la mediana que pasa por B y el punto medio
de AC
Ecuación de la mediana que pasa por C y el punto medio
de AB
Baricentro

50. Baricentro
El baricentro es el punto de corte de las tres
medianas.
Las medianas de un triángulo son las rectas que unen
el punto medio de un lado del triángulo con el vértice
opuesto.
El baricentro se expresa con la letra G.
El baricentro divide a
cada mediana en dos
segmentos, el segmento que
une el baricentro con el
vértice mide el doble que el
segmento que une baricentro
con el punto medio del lado
opuesto.
BG = 2GA

51. Coordenadas del baricentro
A(x1, y1),
B(x2, y2), C(x3,
y3),
Las coorden
adas del
baricentro son:
Ejemplo
Dados los vértices de un triángulo A(-3, -2), B(7, 1) y C(2,
7), hallar las coordenadas del baricentro.

52. Coordenadas del baricentro de un triángulo en el
espacio
Sean A (x1, y1, z1), B (x2, y2, z2) y C (x3, y3, z3) los
vértices de un triángulo, lascoordenadas del baricentro son:
Ejemplos
Sean A = (2, 1, 0), B = (1, 1, 1) y C = (4, 1, −2) los
vértices de un triángulo. Determinar las coordenadas
del baricentro.

53. Dado el triángulo de vértices A(2, 3, 4), B(1, −1, 5) y C(5,
5, 4), hallar:
1. Las ecuaciones de las medianas del triángulo.

54. 2. Las coordenadas del baricentro del triángulo.
3. Las coordenadas del baricentro del triángulo cuyos
vértices son los puntos medios de los lados del triángulo
anterior.
Los baricentros de los dos triángulos coinciden.
Mediatriz
La mediatriz de un segmento es la recta que pasa por
el punto medio del segmento y esperpendicular al él.
Dibujo de la mediatriz de un segmento

55. 1. Trazamos el segmento AB.
2. Con centro en A se traza una circunferencia de radio
mayor que la mitad del segmento AB.
3. Desde B se traza una circunferencia de igual radio que
la primera.
4. La recta que pasa por la intersección de las
circunferencias es la mediatriz del segmento AB.
Punto medio de un segmento
La intersección de la mediatriz con la segmento AB es
el punto medio M.

56. Mediatrices de un triángulo
Las mediatrices de un triángulo son cada una de las
rectas perpendiculares trazadas a unlado por su punto
medio.
Circuncentro
El circuncen
tro es el punto
de corte de
las tres
mediatrices.
El circuncen
tro es
el centro de
una circunferenc
ia
circunscrita al tr
iángulo.
Ecuación de la mediatriz

57. Mediatriz de un
segmento es el lugar
geométrico de
los puntos del
plano que equidistan
de los extremos.
Ejercicios
Hallar la ecuación de la mediatriz del segmento de
extremos A(2 , 5) y B(4, -7).

58. Una recta de ecuación r ≡ x + 2y - 9 = 0 es mediatriz de
un segmento AB cuyo extremo A tiene por coordenadas (2,1).
Hallar las coordenadas del otro extremo.

59. Circuncentro
El circuncentro es el punto de corte de las tres mediatrices.
Las mediatrices de un triángulo son las rectas
perpendiculares trazadas por los puntos medios de sus lados.
El circuncentro se expresa con la letra O.
El circuncentro es el centro de una circunferencia circunscrita
al triángulo.
Bisectrices
La bisectriz de un ángulo es la recta que pasando por
el vértice del ángulo lo divide endos ángulos iguales.

60. Dibujo de la bisectriz
1º Se traza un arco correspondiente al ángulo
2º Desde los dos extremos del arco trazado se trazan, con
cualquier abertura del compás, dos arcos que han de cortarse en
un punto.
3º La bisectriz se obtiene dibujando la recta que une ese
punto con el vértice.
Otra forma de trazar la bisectriz de un ángulo
1.Con centro en el vértice del ángulo se traza una
circunferencia de cualquier amplitud.
2.Desde los puntos de corte de la circunferencia con los
lados del ángulo se trazan dos circunferencias con el mismo
radio.
3.La recta que pasa por el vértice del ángulo y uno de los
puntos de corte de las circunferencias es la bisectriz.

61. Bisectrices de un triángulo
Las bisectrices de un triángulo son las rectas que
dividen a cada ángulo, de los ángulos del triángulo, en dos
ángulos iguales.
Incentro
El incentro es el punto de
corte de las tres bisectrices.
El incentro se expresa con la
letra I.

62. El incentro es el centro de
una circunferencia inscrita en el
triángulo.
Ecuaciones de las bisectrices
La
bisectri
z de un
ángulo
es el
lugar
geomét
rico de
los
puntos
del
plano
que
equidist

63. an de
las
rectas
que
forman
el
ángulo.
Ejercicio
Hallar las ecuaciones de las bisectrices y el incentro del
triángulo de vértices: A(2, 0), B(0, 1) y C(-3, -2).
En primer lugar hallamos las ecuaciones de los lados del
triángulo.

64. Cálculo de la bisectriz que pasa por A.
Cálculo de la bisectriz que pasa por B.

65. Cálculo de la bisectriz que pasa por C.

66. Incentro
El Incentro es el punto de corte de las tres bisectrices
interiores. Para calcularlo, se resuelve el sistema formado por
dos de las ecuaciones.