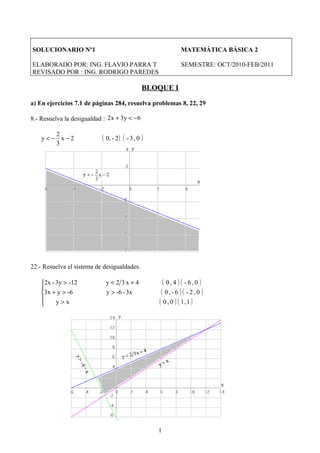
1. SOLUCIONARIO Nº1 MATEMÁTICA BÁSICA 2
ELABORADO POR: ING. FLAVIO PARRA T SEMESTRE: OCT/2010-FEB/2011
REVISADO POR : ING. RODRIGO PAREDES
BLOQUE I
a) En ejercicios 7.1 de páginas 284, resuelva problemas 8, 22, 29
8.- Resuelva la desigualdad : 2 x + 3y < −6
2
y<− x−2 ( 0, - 2) ( - 3 , 0 )
3
22.- Resuelva el sistema de desigualdades.
2x - 3y > -12 y < 2 3x +4 ( 0,4 ) ( -6,0 )

3x + y > -6 y > -6 - 3x ( 0,-6 ) ( -2,0 )
 y>x ( 0 , 0 ) ( 1,1 )

1

2. 29.- Manufactura. Una compañía de sillas produce dos modelos. El modelo Secuoya toma 3 horas
de ensamblado y 1 2 hora de pintura. El modelo Saratoga toma 2 horas de trabajo de
ensamblado y 1 de hora de pintura. El número máximo de horas de trabajo disponibles para
ensamblar sillas es de 240 por día, y el número máximo de horas disponibles para pintura es de
80 diarias. Escriba un sistema de desigualdades lineales para describir la situación. Sea x el
número de modelos Secuoya producidos en un día y el número de modelos Saratoga producidos
en un día. Determine la región para este sistema de desigualdades lineales.
Ensamblado Pintura
Secouya (x) 3 1/2.
Saratoga (y) 2 1
≤240 ≤80
3x + 2y ≤ 240 y ≤ - 3 2 x + 120 ( 0 , 120 ) ( 80 , 0 )

1 2 x + y ≤ 80 y ≤ 80 - x 2 ( 0 , 80 ) ( 160, 0 )
 x,y≥ 0

b) En ejercicios 7.2 de páginas 291-293, resuelva problemas 7, 13, 18
7- Programación lineal.
Minimizar : Z = 7x + 3y
Sujeto a :
3x - y ≥ -2 y ≤ 3x + 2 ( 0 , 2 ) (- 2 3, 0 )
x+y≤9 y ≤9-x ( 0,9 ) ( 9,0 )
x - y = -1 y = x +1 ( 0 ,1 ) (-1, 0 )
x,y≥ 0
2

3. VERTICES: A ( 0 , 1 ) B( 0,2 )
C: 3x + 2 = 9 - x 4x = 7 x=7 4
y = 9-7 4 y = 29 4 C ( 7 4 , 29 4 )
D: x +1 = 9 - x 2x = 8 x=4
y = 4 +1 y=5 D( 4,5 )
VERTICE Z = 7x + 2y Z
A ( 0 ,1 ) 7(0)+2(1) 3
B(0,2) 7(0)+2(2) 6
C ( 7/4 , 29/4 ) 7(7/4)+2(29/4) 34
D(4,5) 7(4)+2(5) 43
Z=3 x=0 y =1
13.- Producción para utilidad máxima. Un fabricante de juguetes prepara un programa de
producción para dos nuevos artículos, camiones y perinolas, con base en la información
concerniente a sus tiempos de ensamblado dados en la tabla que sigue:
Máquina A Máquina B Acabado Utilidad
Camión (x) 2h 3h 5h $7
Perinola (y) 1h 1h 1h $2
Disponibles ≤80 ≤50 ≤70
Por ejemplo, cada camión requiere de 2 horas en la máquina A. Las horas que tienen disponibles
por semana son: para la operación de la máquina A, 80 horas; para la B, 50 horas; para acabado,
70 horas. Si las utilidades en cada camión y cada perinola son de $7 y $2, respectivamente,
¿cuántos juguetes de cada uno deben producirse por semana con el fin de maximizar la utilidad?
¿Cuál es la utilidad máxima?
3

4. Maximizar : Z = 7x + 2y
Sujeto a :
2x + y ≤ 80 y ≤ 80 - 2x ( 0 , 80 ) ( 40, 0 )
3x + y ≤ 50 y ≤ 50 - 3x ( 0 , 50 ) ( 50 3 , 0)
5x + y ≤ 70 y ≤ 70 - 5x ( 0 , 70 ) ( 70 5 , 0)
x,y≥ 0
VERTICES: A ( 0 , 50 ) C ( 70 5 , 0 )
B : 50 - 3x = 70 - 5x 2x = 20 x = 10
y = 50 - 3(10) y = 20 B ( 10 , 20 )
VERTICE Z = 7x + 2y Z
A ( 0 , 50 ) 7(0) + 2(50) 100
B ( 10 , 20 ) 7(10) + 2(20) 110
C ( 70/5 , 0 ) 7(70/5) + 2(0) 98
Z = 110 x = 10 y = 20
18.- Programación de producción. Una compañía petrolera que tiene dos refinerías necesita al
menos 8.000, 14.000 y 5.000 barriles de petróleo de grados bajo, medio y alto, respectivamente.
Cada día, la refinería I produce 2000 barriles de grado bajo, 3000 barriles de grado medio y
1000 barriles de grado alto, en tanto que la refinería II produce 1000 barriles de cada uno de los
grados alto y bajo, y 2000 barriles de petróleo de grado medio. Si operar la refinería I cuesta
$25000 por día, y operar la refinería II $20000 diarios, ¿cuántos días debe operar cada refinería
para satisfacer los requerimientos de producción a un costo mínimo? Suponga que existe un
costo mínimo, ¿Cuál es?
Bajo Medio Alto Costo
Refinería I (x) 2000 3000 1000 $25000
Refinería I (y) 1000 2000 1000 $20000
≥8000 ≥14000 ≥5000
4

5. Minimizar : Z = 25000x + 20000y
Sujeto a :
2000x + 2000y ≥ 8000 y ≥ 8 - 2x ( 0,8 ) ( 4,0 )
3000x + 2000y ≥ 14000 y ≥ 7-3 2 x ( 0 , 7 ) ( 14 3 , 0 )
1000x + 1000y ≥ 5000 y ≥ 5- x ( 0,5 ) ( 5,0 )
x,y≥ 0
VERTICES: A ( 0 , 8 ) D ( 5, 0 )
B: 8 - 2x = 5 - x x =3
y = 5-3 y=2 B( 3, 2 )
C: 5- x = 7-3 2 x x 2= 2 x=4
y = 5-4 y =1 C ( 4 ,1)
VERTICE Z = 25000x + 20000y Z
A(0,8) 25000(0)+20000(8) 160000
B(3,2) 25000(3)+20000(2) 115000
C(4,1) 25000(4)+20000(1) 120000
D(5,0) 25000(5)+20000(0) 125000
Z = 115000 x=3 y=2
BLOQUE II
a) En ejercicios 10.1 de páginas 457-458, resuelva problemas 16, 31, 42
x2 + 6
13.- Determine: lim
x→ - 6 x - 6
5

6. =
( − 6) 2 + 6 = − 21
( − 6) − 6 6
3x 2 - x - 10
31.- Determine: lim 2
x → 2 x + 5x - 14
3(2) 2 - (2) - 10 0 0
= = " FORMA "
(2) 2 + 5(2) - 14 0 0
= lim
( 3x + 5)( x − 2) = lim 3x + 5
x→ 2 ( x + 7 )( x − 2) x → 2 x + 7
3(2) + 5 11
= =
2+5 9
f ( x + h) − f ( x)
42.- Para f ( x ) = 3 − x + 4 x 2 . Determine lim
h→0 h
= lim
[3 - ( x + h ) + 4( x + h ) ] − (3 − x + 4x )2 2
h →0 h
3 - x - h + 4x 2 + 8xh + 4h2 - 3 + x - 4x 2 h ( - 1 + 8x + 4h )
= lim = lim
h →0 h h →0 h
= -1 + 8x + 4(0) = 8x - 1
b) En ejercicios 10.2 de páginas 465-466, resuelva problemas 30, 40, 62
3 - 2x - 2x 3
30.- Determine: lim
x → ∞ 7 - 5x 3 + 2x 2
- 2x 3 -2 2
= lim ; = lim =
x → ∞ - 5x 3 x→∞ -5 5
3x 3 - x 2
54.- Determine: lim
x → -1 2x + 1
62.- Demuestre que lim
x →∞
( x2 + x − x = ) 1
2
( ) (( x2 + x + x ) = lim x + x - x
2 2
+ x + x) ( x + x + x)
= lim x2 + x − x
x →∞ x→∞
x2 2
x x x
= lim
x →∞
( x2 + x ) = lim
x →∞
= lim
x + x x → ∞ 2x
6

7. 1 1
= lim =
x →∞ 2 2
c) En ejercicios 10.4 de páginas 475, resuelva problemas 22, 29
x 2 + 4x − 5
22.- Resuelva la desigualdad: ≤0
x 2 + 3x + 2
f(x) =
( x + 5)( x − 1) f(x) = 0 x = -5 , 1 , - 2 , - 1
( x + 2)( x + 1)
−∞ −5 −2 −1 1 ∞
( -∞,-5 ) f(-6) =
( -)( -) = ( + ) = ( + ) f(x) > 0
( -)( -) ( + )
( -5,-2 ) f(-3) =
( + )( -) = ( -) = ( -) f(x) < 0
( -)( -) ( + )
( - 2 , -1 ) f(-1.5) =
( + )( − ) = ( − ) = ( + ) f(x) > 0
( + )( − ) ( − )
( -1,1 ) f(0) =
( + )( -) = ( -) = ( -) f(x) < 0
( + )( + ) ( + )
( 1, ∞ ) f(2) =
( + )( + ) = ( + ) = ( + ) f(x) > 0
( + )( + ) ( + )
Solución: [ - 5 , - 2 )  ( -1,1 ]
29.- Diseño de un contenedor. Un fabricante de contenedores desea hacer una caja sin tapa,
mediante el corte de un cuadrado de 4 pulgadas en cada esquina de una hoja cuadrada de
aluminio, doblando después hacia arriba los lados. La caja debe contener al menos 324 pulg3.
Encuentre las dimensiones de la hoja de aluminio más pequeña que pueda utilizarse.
7

8. V ≥ 324 ; Ah ≥ 324 ; ( x − 8) ( x − 8) 4 ≥ 324 ; ( x − 8) 2 ≥ 324 4
x 2 − 16 x + 64 ≥ 81 ; x 2 - 16x - 17 ≥ 0
f ( x ) = ( x - 17 ) ( x + 1) ; x = 17, - 1
−∞ -1 17 ∞
( - ∞ , -1 ) f ( - 2 ) = ( −) ( −) = ( + ) f (x)>0
( - 1 , 17 ) f ( 0 ) = ( −) ( + ) = ( − ) f (x)<0
( 17 , ∞ ) f ( 18 ) = ( + ) ( + ) = ( + ) f (x)>0
Solución : [ 17 , ∞ ) Dimensión mas pequeña :17 x 17
d) En ejercicios 11.1 de páginas 488-489, resuelva los problemas 12, 27
12.- Para y = x 2 + 5x + 1 . Encuentre y´
y´= lim
f ( x + h) − f ( x)
y´= lim
[( x + h ) 2
] (
+ 5( x + h ) + 1 − x 2 + 5x + 1 )
h→0 h h →0 h
x 2 + 2xh + h 2 + 5x + 5h + 1 - x 2 - 5x - 1
y´= lim
h →0 h
h ( 2x + h + 5)
y´= lim y´= 2x + 0 + 5
h →0 h
y´= 2x + 5
3
27.- Encuentre la ecuación de la línea tangente a la curva y = , en el punto ( 2 , 3 )
x −1
3 3
−
y´= lím
( x + h) −1 x −1
h →0 h
3( x − 1) − 3( x + h − 1) 3x − 3 − 3x − 3h + 3
y´= lím
( x + h - 1) ( x − 1) = lím ( x + h - 1) ( x - 1)
h →0 h h→0 h
− 3h −3 3
y´= lím = ; y´= −
h → 0 h ( x + h - 1) ( x - 1) ( x + 0 - 1) ( x - 1) ( x − 1) 2
3
y´(2) = − = −3 ; m = -3 ; y - y1 = m ( x - x 1 )
(2 − 1) 2
8

9. y − 3 = −3 (x - 2 ) ; y = -3x + 9
e) En ejercicios 11.2 de páginas 496-497, resuelva los problemas 29, 74, 84, 87
Diferencie las funciones:
9x 2
29.- h(x) = 4x 4 + x 3 - + 8x
2
h´(x) = 16x 3 + 3x 2 - 9x + 8
7x 3 + x
74.- f ( x ) =
6 x
7x 3 x 7 5/2 1 1/2
f(x) = 1/2
+ 1/2 ; f(x) = x + x
6x x 6 6
35 3/2 1 -1/2
f´(x) = x + x
12 12
88.- Encontrar la ecuación de la recta tangente a la curva y =
(
x 2 − x2 )
, cuando x = 4
x
y=
(
x 1/2 2 - x 2 ) ; y = x -1/2 2 - x 2( ) ; y = 2x -1/2 - x 3/2
x
3 1/2 3 25
y´= − x −3 / 2 − x ; y´(4) = m = −(4) −3 / 2 − (4)1/2 ; m=-
2 2 8
y − y1 = m ( x − x 1 ) (x , ? )
y=
(
4 2 − (4) 2
= −7
) ; ( 4 , - 7)
( 4)
25 25 11
y+7 =- ( x - 4) ; y=- x+
8 8 2
87.- Encuentre todos los puntos sobre la curva y = x 2 − 5x + 3 en los que la pendiente es 1.
y´= 2 x − 5 1 = 2x - 5
2x = 6 ; x=3 ; y(3) = (3) 2 - 5(2) + 3 = -3 ( 3 , - 3)
f) En ejercicios 11.3 de páginas 504-506, resuelva problemas 9, 18, 21, 30
9

10. 9.- Ingreso-educación. Los sociólogos han estudiado la relación entre el ingreso y los años de
educación en miembros de un grupo urbano particular. De acuerdo con sus hallazgos, una
persona con x años de educación, antes de buscar empleo regular puede esperar recibir un
ingreso anual medio de y dólares anuales, donde: y = 5x 5 / 2 + 5900 4 ≤ x ≤ 16 . Encuentre la
razón de cambio del ingreso con respecto al número de años de educación. Evalúela cuando
x =9
dy 25 3 / 2
= x
dx 2
dy 25 3 / 2
(9) = (9) = 337.5
dx 2
18.- C = 0.04q 3 − 0.5q 2 + 4.4q + 7500 representa el costo total de producir q unidades de un
producto. Determinar el costo marginal para q = 5 , 25 , 1000
dC
= 0.12q 2 - q + 4.4
dq
dC
(5) = 0.12(5) 2 - (5) + 4.4 = 2.4
dq
dC
(25) = 0.12(25) 2 - (25) + 4.4 = 54.4
dq
dC
(1000) = 0.12(1000) 2 - (1000) + 4.4 = 119.004,40
dq
2 20000
21.- C = 0.00002q − 0.01q + 6 + representa el costo promedio por unidad de producir q
q
unidades de un producto. Encuentre el costo marginal para q = 100 , 500
 20000 
C = C.q C =  0.00002q 2 - 0.01q + 6 +
 .q
 q  
3 2
C = 0.00002q - 0.01q + 6q + 20000
dC
= 0.00006q 2 - 0.02q + 6
dq
dC
(100) = 0.00006(100) 2 - 0.02(100) + 6 = 4.6
dq
dC
(150) = 0.00006(150) 2 - 0.02(150) + 6 = 11
dq
10

11. 30.- Depreciación. Según el método de depreciación lineal, el valor v de cierta máquina después de
t años esta dada por: v = 85000 − 10500 t donde 0 ≤ t ≤ 9 . ¿Qué tan rápido cambia v con
respecto a t cuando t = 2? ¿cuándo t = 3?,¿y en cualquier momento?
dv dv dv
= -10500 (2) = -10500 (3) = -10500
dt dt dt
dv
= -10500 En cualquier instante.
dt
g) En ejercicios 11.4 de páginas 513-515, resuelva los problemas 8, 41, 54,68
Diferencie las funciones:
(
8.- f(x) = 3x 3 x 2 - 2x + 2 )
(
f´(x) = 9x 2 x 2 - 2x + 2 + 3x 3 ( 2x - 2) )
f´(x) = 9x 4 - 18x 3 + 18x 2 + 6x 4 - 6x 3 f´(x) = 15x 4 - 24x 3 + 18x 2
(
f´(x) = 3x 2 5x 2 - 8x + 6 )
x −5
41.- y =
( x + 2)( x − 4)
x −5
y= 2
x − 2x − 8
y´=
(1) (x 2 - 2x - 8) - (x - 5)(2x - 2)
y´=
(
x 2 − 2 x − 8 − 2x 2 − 12 x + 10 )
(x 2 - 2x - 8) 2 (x 2 - 2x - 8) 2
- x 2 + 10x - 18
y´=
(x 2
- 2x - 8 ) 2
x +1
54.- Para y = 2 , encuentre la ecuación de la recta tangente en el punto ( 2,− 3 8)
x ( x − 4)
y´=
(1) [ x 2 ( x − 4) ] − ( x + 1) [2x ( x − 4) − x 2 (1) ] y´=
[x 2
( x − 4) ] − ( x + 1) [2x 2 − 8x + x 2 ]
[ x 2 ( x - 4) ] 2 [ x 2 ( x - 4) ] 2
y´=
(
x 2 ( x − 4 ) − ( x + 1) 3x 2 − 8x )
[ x ( x - 4) ]
2 2
y´(2) = m =
(
(2) 2 ( 2 − 4 ) − ( 2 + 1) 3(2) 2 − 8( 2) )= 4
m=
1
[(2) 2
( 2 - 4) ]
2
64 16
11

12. 3 1 1 1
y − y1 = m ( x − x 1 ) ; y+ = ( x - 2) ; y= x−
8 16 16 4
20 I + 0.5 I 3 − 0.4I
68.- Función de consumo. C = representa la función de consumo. Encuentre
I +5
la propensión marginal al consumo y al ahorro para I = 100 .
Propensión marginal al ahorro = 1 - Propensión marginal al consumo
20I1/2 + 0.5I 3/2 - 0.4I
C=
I1/2 + 5
( )( ) (
dC 10I -1/2 + 0.75I1/2 - 0.4 I1 / 2 + 5 − 20I1 / 2 + 0.5I 3 / 2 − 0.4I (1 2 I −1 / 2 )
=
)
dI I1 / 2 + 5
2
( )
dC
(100) =
(
10(100) -1/2 + 0.75(100)1/2 - 0.4 ((100)1 / 2 + 5) − )
dI (100)1 / 2 + 5
2
( )
( 20(100)
+ 0.5(100) 3/2 - 0.4(100) (1 / 2(100) −1 / 2 )
1/2
)
dC
(100) =
( 8.10)(15) − ( 660)( 0.05) = 0.3933
dI (15) 2
dS dC dS
= 1- ; = 1 - 0.3933 = 0.6067
dI dI dI
h) En ejercicios 11.5 de páginas 521-523, resuelva problemas 16, 44, 59, 67
Diferencie las funciones:
(
16.- y = 2 x 3 − 8x ) −12
(
y´= −12 2 x 3 − 8x ) (6x
−13 2
−8 )
y´= -
(
24 3x 2 - 4 )
( 2x 3
- 8x ) 13
8x 2 − 3
44.- y = 3
x2 + 2
1/3
 8x 2 - 3 
y= 2
x +2

 
12

13. 1  8x 2 − 3 
y´=  2 
-2/3
 ( ) (
 16 x x 2 + 2 − 8x 2 − 3 ( 2x ) 
 )
3 x + 2 
  

2
x +2 (
2 
)
-2/3
1  8x 2 − 3   16 x 3 + 32 x − 16x 3 + 6 x 
y´=  2   
3 x + 2 
  

2
(
x +2
2
)


-2/3
1  8x 2 − 3   38x 
y´=  2   
3 x + 2 
  (
 x2 + 2 ) 2 

y´=
38x
•
8x 2 − 3 ( ) −2 / 3
; y´=
38x
3 (
x2 + 2
−2 / 3
x2 + 2
2
) ( ) (
3 8x 2 − 3 ) (x2/3 2
+2 ) 4/3
59.- Encuentre la ecuación de la recta tangente a la curva y = 3 x 2 − 8 ( ) 2
en el punto ( 3 , 1 )
(
y = x2 -8 ) 2/3
y´=
2 2
3
(
x - 8 ( 2x )
-1/3
) ; y´=
4x 2
3
(
x -8
-1/3
)
y´(3) = m =
4(3)
3
(
(3) 2 - 8
-1/3
) ; m=4
y − y1 = m ( x − x 1 ) ; y - 1 = 4( x - 3) ; y = 4x - 11
10m 2
67.- q = es el número de unidades producidas por día por m empleados de un fabricante,
m2 + 9
525
y p= es el precio por unidad. Encuentre el producto de ingreso marginal para m = 4
q+3
dr dr dm
= • " Producto de ingreso marginal"
dm dm dq
 525  525q
r = p.q ; r=
 q + 3.q
 ; r=
  q+3
dr 525( q + 3) − 525q
=
dq ( q + 3) 2
10( 4 ) 2
m=4 ; q= = 32
2
(4) + 9
13

14. dr
( 320) = 525( 32 + 3) − 525( 32) = 1.2857
dq ( 32 + 3) 2
10m 2
q=
(m 2
+9 ) 1/ 2
dq
(
20m m 2 + 9 ) 1/ 2
− 10m 2 1 2 m 2 + 9


( ) −1 / 2
( 2m ) 


=
dm
(
 m2 + 9


) 1/ 2  2


dq 20m m 2 + 9
=
(− 10m 3 m 2 + 9 ) 1/ 2
( ) −1 / 2
dm m2 + 9
dq
(4) =
20(4) (4) 2 + 9 (
− 10(4) 3 (4) 2 + 9) 1/ 2
( ) −1 / 2
=
400 - 128
= 10.88
dm (4) 2 + 9 25
dr
= 1.2857 • 10.88 = 13.99
dm
14