1. intervalo de confiança parte i
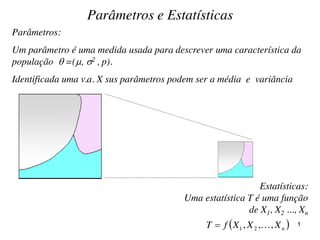
- 1. Parâmetros: Um parâmetro é uma medida usada para descrever uma característica da população =(, 2 , p). Identificada uma v.a. X sus parâmetros podem ser a média e variância Estatísticas: Uma estatística T é uma função de X1, X2 ..., Xn Parâmetros e Estatísticas nXXXfT ,,, 21 1
- 2. Parâmetros e Estatísticas )pˆ,ˆ,ˆ(ˆ 2 Parâmetros: =(, 2 , p) Estimativas: n x psX ˆˆˆ 22 2
- 3. )(X n Xi X )(2 XVar )1/()( 22 nXxS i Denominação População Amostra N de elementos N n Média Variância Proporção p pˆ Símbolos mais comuns a seguir 3
- 4. Amostras Distribuição amostral da estatística T 4
- 5. População com media Uma amostra aleatória simples de n elementos é selecionada a partir da população Os dados da amostra fornecem um valor para a média da amostra X O valor de é usado para fazer inferências sobre o valor de X O valor esperado de iguala-se a a partir da qual a amostra é extraída. X 5 1 23 4
- 6. Teorema Central do Limite Dado que : • A variável aleatória X tem distribuição (que pode ser normal, ou não), com média e desvio padrão . • Amostra de tamanho “n” são extraídas aleatoriamente dessa população. 6
- 7. Teorema Central do Limite Conclusões: • Na medida que o tamanho da amostra aumenta, a distribuição das médias amostrais tende para uma distribuição normal. • A média das médias amostrais será a média populacional. • O desvio padrão das médias amostrais será x nx 7
- 8. Teorema Central do Limite Regras Práticas de Uso Comum: • Para amostras de tamanho n > 30, a distribuição das médias amostrais pode ser aproximada satisfatoriamente por uma distribuição normal. • Se a própria distribuição original tem distribuição normal, então as médias amostrais terão distribuição normal para qualquer tamanho amostral n. X 8
- 9. Intervalo de Confiança IC Um intervalo de confiança (ou estimativa intervalar) é uma amplitude (ou um intervalo) de valores que tem probabilidade de conter o verdadeiro valor do parâmetro populacional. =(,2 , p) )()( xUxL 9
- 10. Intervalo de Confiança IC A partir de uma amostra de uma distribuição f(x,), que depende de um parâmetro desconhecido, desejamos encontrar um intervalo aleatório que contenha com alta probabilidade é chamado de intervalo de confiança (1-) se )()( xUxL 1)()(Pr xUxL 10
- 11. Estimação: Um estimador é uma estatística amostral utilizada para obter uma aproximação de um parâmetro populacional. )pˆ,ˆ,ˆ(ˆ 2 Uma estimativa pontual é um valor (ou ponto) único usado para aproximar um parâmetro populacional. n x psX ˆ,ˆ,ˆ 22 11
- 12. Estimativa de uma Média Populacional: Grandes Amostras Coeficiente de confiança é a probabilidade ( 1- ) de o intervalo de confiança conter o verdadeiro valor do parâmetro populacional. Coeficiente de Confiança (1- ) /2/2 12
- 13. Coeficiente de Confiança (1- ) /2/2 z/2- z/2 A distribuição normal padronizada o valor z/2 é o valor crítico O grau de confiança é também chamado de nível de confiança ou coeficiente de confiança. Estimativa de uma Média Populacional: Grandes Amostras 13
- 14. Valores críticos mais comuns: 1 - 0,80 0,85 0,90 0,95 0,99 z/2 1,28 1,44 1,645 1,96 2,58 /2 /2 1 - 0 z/2- z/2 Normal(0,1) 14
- 15. A margem de erro, denotado por E é a diferença máxima provável (com probabilidade 1- ) entre a média amostral observada e a verdadeira média populacional .X A margem de erro pode ser obtida multiplicando-se o valor crítico pelo desvio padrão das médias amostrais, n .zE 2 Margem de Erro 15
- 16. Áreas de uma distribuição amostral de usada para fazer declarações de probabilidade sobre o erro de amostragem /2 /2 Distribuição amostral da X (1- )% X n z 2/ 16
- 17. Tamanho da Amostra para estimar Pode-se aplicar a fórmula E também para determinar o tamanho da amostra que é necessário para atingir um grau de precisão desejado . Resolvendo a equação do erro em n obtemos, 2 2 E z n n .zE 2 17
- 18. Intervalo de Confiança para a média populacional (com base a grandes amostras: n > 30) EXEX Onde n .zE 2 n zX; n zX 22 Outras formas equivalentes de escrever: • com variância conhecida o intervalo de confiança 100(1-)% para Intervalo de Confiança (IC) para • com variância desconhecida, usa-se a distribuição normal com o estimador s2 de 2 . 18
- 19. Intervalo de Confiança (IC) para Exemplo 1: Sejam X1, X2, ... X40 uma amostra aleatória de uma variável aleatória que tem distribuição Normal com média desconhecida e variância = 410. Se encontre um intervalo de confiança 95% para .. 1428X Olhando a tabela da Distribuição Normal, temos que o ponto crítico, tal que Se = 0,05, temos que z0,025 = 1,96. 2/2/ zZP 19
- 20. Intervalo de Confiança (IC) para Pr[Z > 1,96 ] = 0,025Pr[Z < - 1,96]= 0,025 - 1,96 Pr[-1,96 < Z < 1,96] = 0,95 1,96 O IC de 95% de confiança para a é [1300,85 ; 1555,15] 20 X - z(∝/2)*σ/√n = = 1428 - 1,96*410/√40 = = 1.300,94 X + z(∝/2)*σ/√n = = 1428 + 1,96*410/√40 = = 1.555,06
- 21. Intervalo de Confiança para a média populacional (com base a pequenas amostras: n < 30) Variáveis aleatórias independentes, então: • com variância desconhecida Intervalo de Confiança (IC) para Pode-se mostrar que: e2 1n 2 ~ S)1n( )1,0(Normal~ X n 1nt~ S Xn 21
- 22. Intervalo de Confiança para a média populacional (com base a pequenas amostras: n < 30) n s tX n s tX nn 11 ; • com variância desconhecida Intervalo de Confiança (IC) para O intervalo de confiança 100(1-)% para Onde t é o percentil (1 - /2) da distribuição de Student com n -1 graus de liberdade. 22
- 23. Intervalo de Confiança (IC) para n s tX n s tX nn 11 ; /2 /2 tn-1- tn-1 Pr[ t > tn-1] = /2 Ex. Se n = 10 e = 0,05, temos Pr[ t < 2,262] = 0,975 23
- 24. Intervalo de Confiança (IC) para Exemplo 2: Sejam X1, X2, ... X40 uma amostra aleatória de uma variável aleatória que tem distribuição Normal com média e variância desconhecidas. Dado que e s= 496, encontre um intervalo de confiança 95% para . 1428X Se n > 30, então usa-se a distribuição normal com estimador s2 de 2. 24
- 25. Intervalo de Confiança (IC) para Pr[Z > 1,96 ] = 0,025Pr[Z < - 1,96]= 0,025 - 1,96 Pr[-1,96 < Z < 1,96] = 0,95 1,96 O IC de 95% de confiança para a é [1274,18 ; 1581,82] 25 X - t(n-1)*s/√n = = 1428 - 1,96*496/√40 = = 1.274,29 X - t(n-1)*s/√n = = 1428 + 1,96*496/√40 = = 1.581,71
- 26. Intervalo de Confiança (IC) para Exemplo 3: Sejam X1, X2, ... X25 uma amostra aleatória de uma variável aleatória que tem distribuição Normal com média e variância desconhecidas. Dado que e s2 = 36, encontre um intervalo de confiança 95% para . 15X Olhando a tabela da Distribuição t de Student, temos que o ponto crítico t24,0,025=2,064 então Pr[t24 > 2,064] = 0,025. 26
- 27. Intervalo de Confiança (IC) para Pr[t > 2,064 ] = 0,025Pr[t < - 2,064]= 0,025 - 2,064 Pr[-2,064 < t < 2,064] = 0,95 2,064 O IC de 95% de confiança para a é [ 12,523 ; 17,477] 27 X + t(n-1)*√s²/√n = = 15 + 2,064*√36/√25 = = 17,477 X - t(n-1)*√s²/√n = = 15 - 2,064*√36/√25 = = 12,523
- 28. Lembrando que quando p populacional é conhecida, tem distribuição assintotica . pp zpzp ˆ0ˆ0 22 ˆ;ˆ Logo, temos que o IC para a proporção populacional ao nível de significância (1-) : Intervalo de Confiança (IC) para proporções n x p ˆ n pq pNp ,ˆ Para construir o IC para p desconhecida, determinarmos na amostra e consideremos 0 ˆp n qp p 00 ˆ ˆˆ 28
- 29. Exemplo: Retiramos de uma população uma amostra de 100 elementos e encontramos 20 sucessos. Ao nível de 1%, construir um IC para a proporção real de sucessos na população. Intervalo de Confiança (IC) para proporções 29 O IC de 99% de confiança para p é [ 0,0972; 0,3028] p(o) - z(∝/2)*σ(p) = = 0,01 - 2,58*?? = = p(o) + z(∝/2)*σ(p) = = 0,01 + 2,58*?? = =
- 30. Aumentando o tamanho da amostra para melhorar a precisão. •Uma maneira de melhorar a precisão do intervalo de confiança sem diminuir o nível de confiança é aumentar o tamanho da amostra. Obtendo o tamanho mínimo da amostra para estimar p Dado um nível de confiança (1-) e um erro máximo de estimativa E, o mínimo tamanho necessário da amostra para estimar p é Essa formula supõe que haja uma estimativa preliminar para e . Caso não seja assim, use e 30 2 2/ ˆˆ E z qpn pˆ qˆ 5,0ˆ p 5,0ˆ q
- 31. Determinando um tamanho mínimo para a amostra. •Você é auxiliar em uma campanha política e deseja estimar, com 95% de confiança, a proporção de eleitores registrados que votarão em seu candidato. •Qual é o mínimo tamanho necessário da amostra para estimar a proporção populacional com precisão dentro de 3%? Solução: Uma vez que não temos estimativas preliminares usaremos e . Usando e E=0,03 temos que Pelo menos 1.068 eleitores registrados devem ser incluídos na amostra. Exemplo 5,0ˆ p 31 5,0ˆ q 96,12/ z 11,1067 03,0 96,1 )5,0)(5,0(ˆˆ 22 2/ E z qpn
- 32. População Normal com média desconhecida. 1 11 2 1 2 2 2 2 2 snsn P Logo, o IC para a proporção populacional ao nível de significância (1-) : Intervalo de Confiança (IC) para a variância 2 1 2 1 2 n n i i xx Demostra-se que tem distribuição relacionada com com (n-1) graus de liberdade, isto é, n i i xx 1 2 2 Como temos 22 1 1 xx n s i 2 1 2 1 snxx n i i 22 1 2 1 snn 32
- 33. 1 11 2 1 2 2 2 2 2 snsn P O IC para a variância populacional ao nível de significância (1-) : Intervalo de Confiança (IC) para a variância Onde: e 2 )%2/(,1 2 1 n 2 )%2/1(,1 2 2 n 33
- 34. Exemplo: Sabe-se que o tempo de vida de certo tipo de válvula tem distribuição aproximadamente normal. Uma amostra de 25 válvulas forneceu média amostral de 500 h e s=50 h. Construir um IC para 2, ao nível de 2%. Intervalo de Confiança (IC) para a variância Se n = 25, s2=2500 856,102 %1,24 2 1 980,422 %99,24 2 2 1 11 2 1 2 2 2 2 2 snsn P 34 O IC de 98% de confiança para 2 é [ 1395,9; 5526,9] (n-1)*s²/x2² = = (25-1)*2500/42,980 = = 1.396 (n-1)*s²/x1² = = (25-1)*2500/10,856 = = 5.526,90
