Calculo de superficies usando integrales, además al final un gráfico en varias dimensiones.

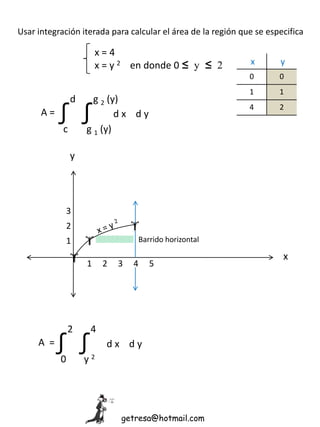
1. Usar integración iterada para calcular el área de la región que se especifica
x = 4
x = y 2 en donde 0 ≤ y ≤ 2
A = ∫
d
c
∫
g 2 (y)
g 1 (y)
d x d y
x y
0 0
1 1
4 2
A =∫
2
0
∫
4
y 2
d x d y
y
x
1 2 3 4 5
3
2
1 


▒▒▒▒▒▒▒▒▒ Barrido horizontal
getresa@hotmail.com

2. A =∫
2
0
4
y 2
d y
│x
A =∫
2
0
( 4 – y 2 ) d y
A =∫
2
0
4 d y – y 2 d y∫
2
0
│A =
2
0
4 y y 3
3
2
0
│
A = 4 (2) – 4 (0) –
(2) 3
3
(0) 3
3
–
A = 8 –
8
3
A = 5,33 cm 2
–
getresa@hotmail.com

3. y
x
1 2 3 4 5
3
2
1 


▒
▒
▒
▒
Barrido vertical
x = y
x
x
A =∫
4
0
∫
0
d y d x
A =∫
4
0 0
d x
│y
A =∫
4
0
x – 0 d x
1/2
3/2
A = x
3
2
│
4
0
getresa@hotmail.com

4. A =
2
3
4 3
( )
A =
2
3
( 8 )
A = 5,33 cm 2
Observación: tanto barrido horizontal como vertical dan el mismo resultado
getresa@hotmail.com

5. y
x1 2 3 4 5 6 7 8 9
4
3
2
1
▓▓▓▓▓▓▓▓▓▓▓▓▓▓▓▓▓▓▓▓▓▓▓▓
A = ∫
3
0
∫
8
0
d x d y
A = ∫
3
0
│
8
0
d yx
A = ∫
3
0
8 d y
A = 8 y │
3
0
A = 8 (3) – 8 (0)
A = 24 cm 2
Barrido horizontal
getresa@hotmail.com

6. x y
0 4
1 3
2 0
– 1 3
– 2 0
y = 4 – x 2
x en donde 0 ≤ x ≤ 2
y
x
1 2 3 4
5
4
3
2
1
-4 -3 -2 -1
▒
▒
▒
▒
▒
A = ∫
2
0
∫
4 – x 2
0
d y d x
A = ∫
2
0
│
0
d xy
4 – x 2
getresa@hotmail.com

7. A = ∫
2
0
(4 – x 2 ) d x
A = ∫
2
0
4 d x –
∫
2
0
x 2 d x
│ │A = 4 x –
2
0
x 3
3
2
0
A = 4 (2) –
(2) 3
3
24 – 8
3
A =
A = 5,33 cm 2
getresa@hotmail.com

8. y = 4 – x 2
y = x + 2
x y
0 4
1 3
2 0
– 1 3
– 2 0
– 3 – 5
x y
0 2
1 3
2 4
– 1 1
– 2 0
y = 4 – x 2 y = x + 2
y
x
1 2 3 4
5
4
3
2
1
-4 -3 -2 -1

 


- 1
- 2
- 3
- 4
- 5
▒
▒
▒
Calcular el área entre las
2 ecuaciones
getresa@hotmail.com

9. A = ∫
1
– 2
∫
4 – x 2
x + 2
d y d x
A = ∫
1
– 2
4 – x 2
x + 2
d xy│
1
A = ∫
– 2
( 4 – x 2 ) – ( x + 2 ) d x
1
A = ∫
– 2
( – x 2 – x + 2 ) d x
A =
x 3
3
x 2
2
– – + 2 x │
1
– 2
A =
(1)3
3
(1) 2
2
– – + 2 (1) –
(– 2) 3
3
(– 2) 2
2
– – + 2 (– 2)
A =
1
3– –
1
2 + 2 –
8
3 + 6
A = 4,5 cm 2
1
2
A = 5 –
getresa@hotmail.com

10. Graficar y calcular superficie
y = 4 x – x 2
y = – 3 x + 6
4 x – x 2 = – 3 x + 6
– x 2 + 4 x + 3 x – 6 = 0
– x 2 + 7 x – 6 = 0
Multiplico por – 1 la ecuación ya que no puede ser negativo x 2
x 2 – 7 x + 6 = 0
La ecuación es uno de los diez casos de factorización:
( x – 6 ) ( x – 1 ) = 0
x – 6 = 0  x = 6
x – 1 = 0  x = 1
Remplazando x en cualquiera de las ecuaciones originales
obtenemos y:
y = – 12
y = 3
( 6 , – 12 ) ( 1 , 3 )
y = 4 x – x 2
y = – x 2 + 4 x
a b
b
x = –
2 a
4
= –
2 (– 1 )
= 2
getresa@hotmail.com

11. Remplazo en una de las ecuaciones originales:
y = 4 ( 2 ) – ( 2 ) 2
y = 4
Punto máximo en la ecuación (curva) 4 x – x 2 ( 2, 4 )
y = 4 x – x 2 y = – 3 x + 6
x y
0 0
1 3
2 4
3 3
4 0
5 – 5
6 – 12
– 1 – 5
– 2 – 12
x y
0 6
1 3
2 0
3 – 3
4 – 6
5 – 9
6 – 12
– 1 9
getresa@hotmail.com

12. - 1
-2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
5
4
3
2
1
1 2 3 4 5 6 7-3 -2 -1












9
8
7
6




( 2, 4)
( 6, – 12 )
(1, 3)
x
y
1 er cuadrante2 do cuadrante
3 er cuadrante 4 to cuadrante
getresa@hotmail.com

13. El área que se encuentra en el primer cuadrante entre las dos
ecuaciones es el que vamos a calcular con el uso de integrales.
4 x – x 2 4 x – x 2
d y d x + d y d x =∫∫∫ ∫
2
2 4
1 0– 3x + 6
4 x – x 2 4 x – x 2
d x + d x =│∫ ∫
2
2 4
1 0– 3x + 6
y y │
∫
2
1
4 x – x 2 – (– 3 x + 6 ) dx + ∫
2
4
4 x – x 2 – 0 dx =
∫
2
1
( 4 x – x 2 + 3 x – 6 ) dx + ∫
2
4
( 4 x – x 2 ) dx =
∫
2
1
∫
2
1
∫
2
1
7 x dx – x 2 dx – 6 dx +∫
2
4
4 x dx – ∫
2
4
x 2 dx =
1
7 x 2
2
x 3
3
– 6 x– +
4 x 2
2
x 3
3
– =│ │
2 4
2
getresa@hotmail.com

14. Después de realizar las integrales, remplazo x con los
valores correspondientes:
7 (2) 2
2
(2) 3
3
– 6 (2) ––
7 (1) 2
2
–
(1) 3
3
– 6 (1) +( )
4 (4) 2
2
(4) 3
3
– ( )4 (2) 2
2
(2) 3
3
–– =
28
2
8
3
– 12 ––
7
2
–
1
3
– 6 +( )
64
2
64
3– ( )8
2
8
3
–– =
1
3
64
3
8
3
14 – 8
3
– 12 – + 6 + 32 – – 8 +
7
2
+ =
32 – –
7
2
63
3
=
192 – 21 – 126
6
=
45
6
= 7,5 cm 2
getresa@hotmail.com

15. Intersección de planos
z = 16 – 4 x 2 – y 2
Este tipo de ecuaciones las podemos graficar igualando a cero
cada una de las variables, tenemos tres variables, empezaré
por z.
(0) 2 = ( 16 – 4 x 2 – y 2 )
0 = 16 – 4 x 2 – y 2
4 x 2 + y 2 = 16
Igualare a 0 x, para encontrar el valor de y.
y 2 = 16
y 2 = 16
y = ± 4
Es el turno de igualar y a 0
4 x 2 = 16
x 2 = 16 / 4
x 2 = 4
x = ± 2
El gráfico en un plano de 2 ejes sería el siguiente:
Al hablar de ejes estoy hablando del plano cartesiano el cual es
de dos dimensiones pero pueden existir de muchas
dimensiones.
2
getresa@hotmail.com

16. y
– y
x– x
1 2– 2 – 1
4
3
2
1
– 1
– 2
– 3
– 4
Igualaré x a cero en la ecuación original
z = 16 – y 2
z 2 = ( 16 – y 2 )
z 2 = 16 – y 2
z 2 + y 2 = 16
Igualaré a cero z y y respectivamente para representarlo en el
plano cartesiano
y 2 = 16
y = ± 4
2
getresa@hotmail.com

17. z 2 = 16
z = ± 4
El gráfico queda de la siguiente manera:
z
– z
y– y
1 2 3 4– 4 – 3 – 2 – 1
4
3
2
1
– 1
– 2
– 3
– 4
getresa@hotmail.com

18. Igualaré a cero y en la ecuación original
z = 16 – 4 x 2
z 2 = ( 16 – 4 x 2 )
z 2 = 16 – 4 x 2
z 2 + 4 x 2 = 16
Igualaré a cero z y x respectivamente para representarlo en el plano
cartesiano
4 x 2 = 16
x 2 = 16 / 4
x 2 = 4
x = ± 2
z 2 = 16
z = ± 4
2
z
– z
x– x
1 2– 2 – 1
4
3
2
1
– 1
– 2
– 3
– 4
getresa@hotmail.com

19. Representando los gráficos en un solo plano en R 3.
x
y
z
¤
¤
¤
¤
¤
Cuando z = 0
¤ – x
– y
Cuando y = 0
Cuando x = 0
– z
getresa@hotmail.com