Presentación adaptada a partir de una presentación del profesor

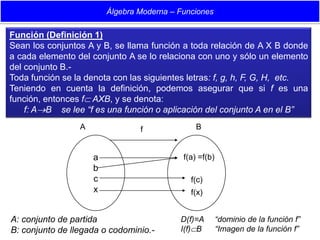
1. Álgebra Moderna – Funciones
Función (Definición 1)
Sean los conjuntos A y B, se llama función a toda relación de A X B donde
a cada elemento del conjunto A se lo relaciona con uno y sólo un elemento
del conjunto B.-
Toda función se la denota con las siguientes letras: f, g, h, F, G, H, etc.
Teniendo en cuenta la definición, podemos asegurar que si f es una
función, entonces f AXB, y se denota:
f: AB se lee “f es una función o aplicación del conjunto A en el B”
A f B
a f(a) =f(b)
b
c f(c)
x f(x)
A: conjunto de partida D(f)=A “dominio de la función f”
B: conjunto de llegada o codominio.- I(f)B “Imagen de la función f”

2. Álgebra Moderna – Funciones
Función (Definición 2):
La relación fAXB es una función si cumple con las siguientes condiciones
de existencia y unicidad:
Existencia
Todo elemento de A se relaciona con algún elemento de B
xA,yB/(x,y)f
Unicidad
Los elementos de A tienen una sola imagen en B
(x,y)f  (x,z)f  y = z
Función (Definición 3):
Se define función como la relación entre las variables “x” e “y”, donde a cada uno
de los valores que pueda tomar “x”, lo relaciona con uno y solo un valor de “y”
y=f(x)

3. Álgebra Moderna – Funciones
CLASIFICACIÓN DE LAS FUNCIONES
FUNCIÓN INYECTIVA
f:AB es inyectiva si y sólo si elementos distintos del dominio tienen
imágenes distintas. O sea:
f : A  B es inyectiva  x1 , x2 : x1  x2  f ( x1 )  f ( x2 )
f : A  B es inyectiva  x1 , x2 : f ( x1 )  f ( x2 )  x1  x2

4. Álgebra Moderna – Funciones
FUNCIÓN SOBREYECTIVA O SURYECTIVA
f:AB es sobreyectiva si y sólo si todos los elementos del Codominio
tienen preimagen. O sea:
f : A  B es sobreyecti  y  B, x  A / f ( x)  y
va

5. Álgebra Moderna – Funciones
FUNCIÓN BIYECTIVA
Una función es biyectiva si y sólo si es inyectiva y sobreyectiva.
CONCLUSIÓN:
Haciendo un análisis sobre la clasificación de las funciones, podemos
concluir que:
• Una función puede ser inyectiva, solamente
• Una función puede ser sobreyectiva, solamente
• Una función puede ser inyectiva y sobreyectiva (biyectiva)
• Una función puede no ser inyectiva ni sobreyectiva

6. Álgebra Moderna – Funciones
COMPOSICIÓN DE FUNCIONES
Sean dos funciones, f:AB  g:BC, se llama composición de las
funciones f y g a la función gof:AC/gof(x)=g[f(x)], siempre que exista un
elemento yB tal que y=f(x), y z=g(y), con zC y xA,
A B C
f g
x y=f(x) z=g[f(x)]
gof

7. Álgebra Moderna – Funciones
POR EJEMPLO
Sean las funciones
1
f : R  R / f ( x)  x  2 g : (2, )  R / g ( x)  log( x  2)
3
Determinar gof:(2,)R
gof ( x)  g  f x 
gof ( x)  log f ( x)  2
1 
gof ( x)  log  x  2  2 
3 
1 
gof ( x)  log  x  4 
3 

8. Álgebra Moderna – Funciones
PROPIEDADES DE LA COMPOSICIÓN
1. ASOCIATIVIDAD DE LAS COMPOSICIÓN DE FUNCIONES
La composición de funciones es asociativa.
H) Sean las funciones
f :A B
g:BC
h:C  D
T) ho( gof )  (hog)of
D) Como la composición de funciones está definida sólo para tres conjuntos, o dos
funciones, debemos trabajar éstas para poder aplicar dicha definición para las tres
funciones. Para ello desarrollamos ambos miembros de la igualdad de la Tesis:
gof : A  C 
  ho( gof )(x)  hog  f x   hg  f x  (A)
h:C  D 
f : A B 
  (hog )of ( x) (hog ) f ( x)  hg  f x  (B)
hog : B  D
ho(gof)=(hog)of

9. Álgebra Moderna – Funciones
2. COMPOSICIÓN DE FUNCIONES INYECTIVAS
La composición de funciones inyectivas es inyectiva
H) Sea f:AB  g:BC inyectivas
T) gof:AC es inyectiva
D) Teniendo en cuenta que y=f(x) y z=g(y) son inyectivas, entonces:
x1 , x2 : f ( x1 )  f ( x2 )  x1  x2 y1 , y 2 : g ( y1 )  g ( y 2 )  y1  y 2
Ahora
gof ( x1 )  gof ( x2 )
g  f ( x1 )  g  f ( x2 )
f ( x1 )  f ( x2 )
x1  x 2
 gof:AC es inyectiva (por definición de inyectividad).-

10. Álgebra Moderna – Funciones
3. COMPOSICIÓN DE FUNCIONES SOBREYECTIVAS
La composición de funciones sobreyectivas, es sobreyectiva
H) Sea f:AB  g:BC sobreyectivas
T) gof:AC es sobreyectiva
D) Como y=f(x) y z=g(y) son sobreyectivas, entonces:
y  B, x  A / f ( x)  y z  C, y  B / g ( y)  z
Ahora, teniendo en cuenta la composición de funciones y por hipótesis y
por las aseveraciones hechas anteriormente, tenemos:
z  C , x  A / g  f ( x)  g ( y)  z
Pero,
g  f ( x)  gof ( x)
por definición de composición de funciones, lo que se tiene que
gof ( x)  z
Luego, gof:AC es sobreyectiva

11. Álgebra Moderna – Funciones
4. COMPOSICIÓN DE FUNCIONES BIYECTIVAS
La composición de funciones biyectivas, es biyectiva
H) Sea f:AB  g:BC biyectivas
T) gof:AC es biyectiva
D) Por definición, una función es biyectiva solamente si es inyectiva y
sobreyectiva, y teniendo en cuenta las demostraciones de composición de
funciones inyectivas y composición de funciones sobreyectivas, se
demuestra esta propiedad.-

12. Álgebra Moderna – Funciones
TEOREMA FUNDAMENTAL DE LAS FUNCIONES INVERSAS
Una función admite inversa si y sólo si es biyectiva
f:AB admite inversa  es biyectiva
Para demostrar este teorema, debemos desdoblar la doble implicación, o sea
H) f:AB admite inversa
T) f es biyectiva
D) Como la función admite inversa (hipótesis), entonces:
gof(x)=iA(x)=x  fog(y)=iB(y)=y
Hacemos:
gof ( x1 )  gof ( x2 )
i A ( x1 )  i A ( x 2 )
x1  x 2
Lo que significa que f es INYECTIVA

13. Álgebra Moderna – Funciones
Ahora:
y  i B ( y)  fog ( y)  B, x  i A ( x)  gof ( x)  A / f ( x)  f gof ( x) 
 f ( x)   fo gof ( x)
Pero por la propiedad asociativa de la composición de funciones, queda:
f ( x)  ( fog )of ( x)
Y aplicando la definición de composición, se tiene:
f ( x)  ( fog ) f ( x)
f ( x)  ( fog)( y)
f ( x)  y
Esto demuestra que la función f es SOBREYECTIVA
Luego, la función f es BIYECTIVA (por definición de función biyectiva)

14. Álgebra Moderna – Funciones
Demostremos ahora la segunda parte:
H) f:AB es biyectiva
T) f admite inversa
D) Para poder demostrar esta parte del teorema, debemos encontrar una
función g:BA, siempre que exista f:AB de tal forma que x=g(y), si
y=f(x).-
Ahora, para que g sea función debe cumplir con las condiciones de
existencia y unicidad.-
Bajo las condiciones descriptas anteriormente, como f es biyectiva, y en
particular sobreyectiva, entonces todos los elementos de B tienen
antecedente en A por f, lo que significa que todos los elementos de B
tienen imagen en A por g (existencia).
Por otro lado, como f es inyectiva, entonces distintos elementos de A tienen
imagen distinta en B por f, lo que significa que por g, los elementos de B
tienen una y sólo una imagen (unicidad).
Luego g:AB es función

15. Álgebra Moderna – Funciones
Ahora como f y g son funciones, podemos hacer la composición de ellas y
obtener una conclusión:
gof ( x)  g  f ( x)
Pero por lo dicho anteriormente y=f(x), entonces:
gof ( x)  g ( y)
Por la misma razón que la anterior x=g(y), entonces
gof ( x)  x  i A ( x)
Por otro lado se tiene: fog ( y)  f g ( y)
Pero por lo dicho anteriormente x=g(y), entonces:
fog( y)  f ( x)
Por la misma razón que la anterior y=f(x), entonces
fog ( y)  y  i B ( y)
Luego la función f admite inversa, y es la función g
Habiendo demostrado estas dos partes, quedó demostrado el teorema.-

16. REALIZACION
Prof. LUIS ERNESTO VALDEZ
Departamento de Matemática
Instituto de Estudios Superiores de Andalgalá
2008 - 2012