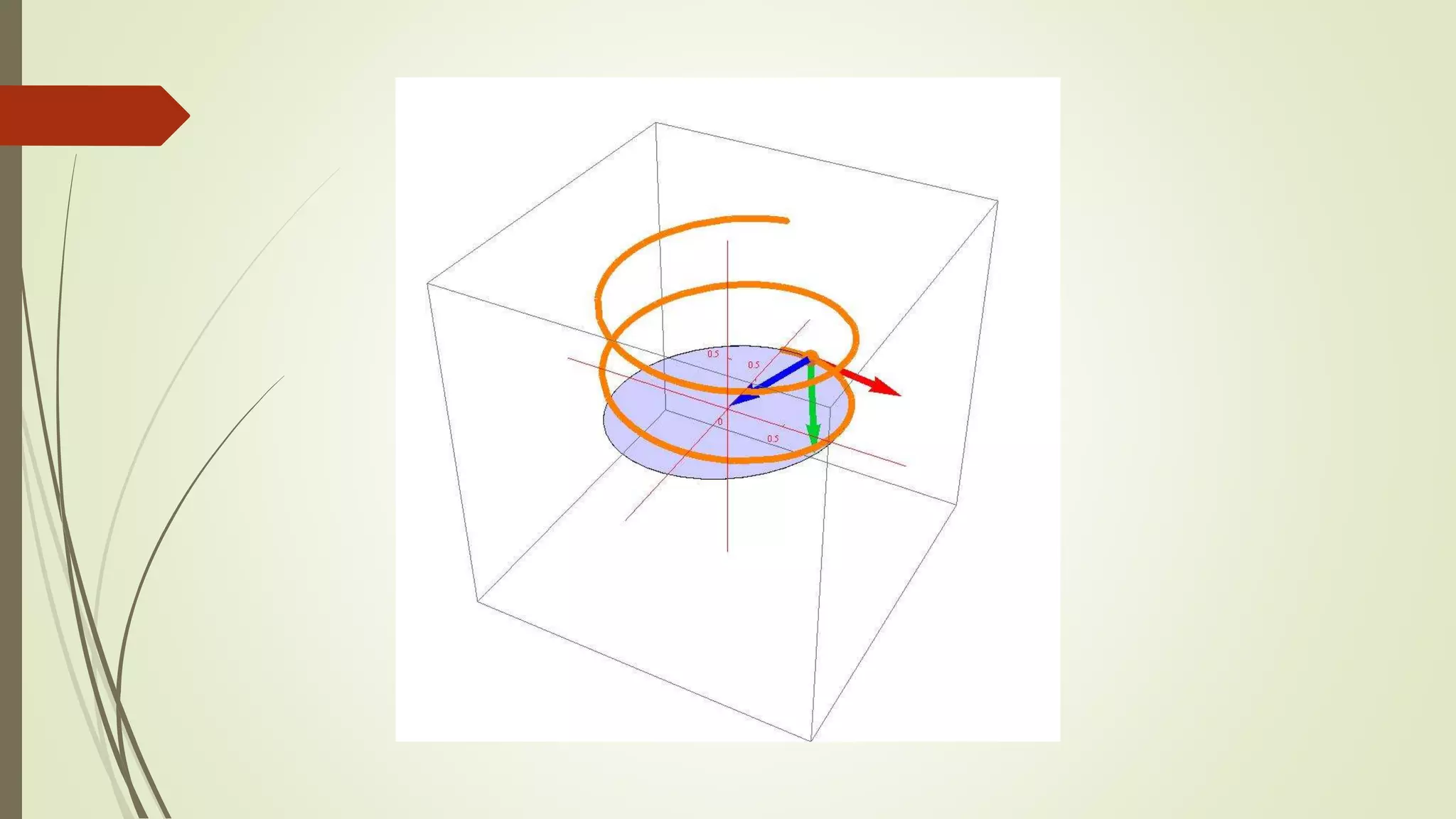
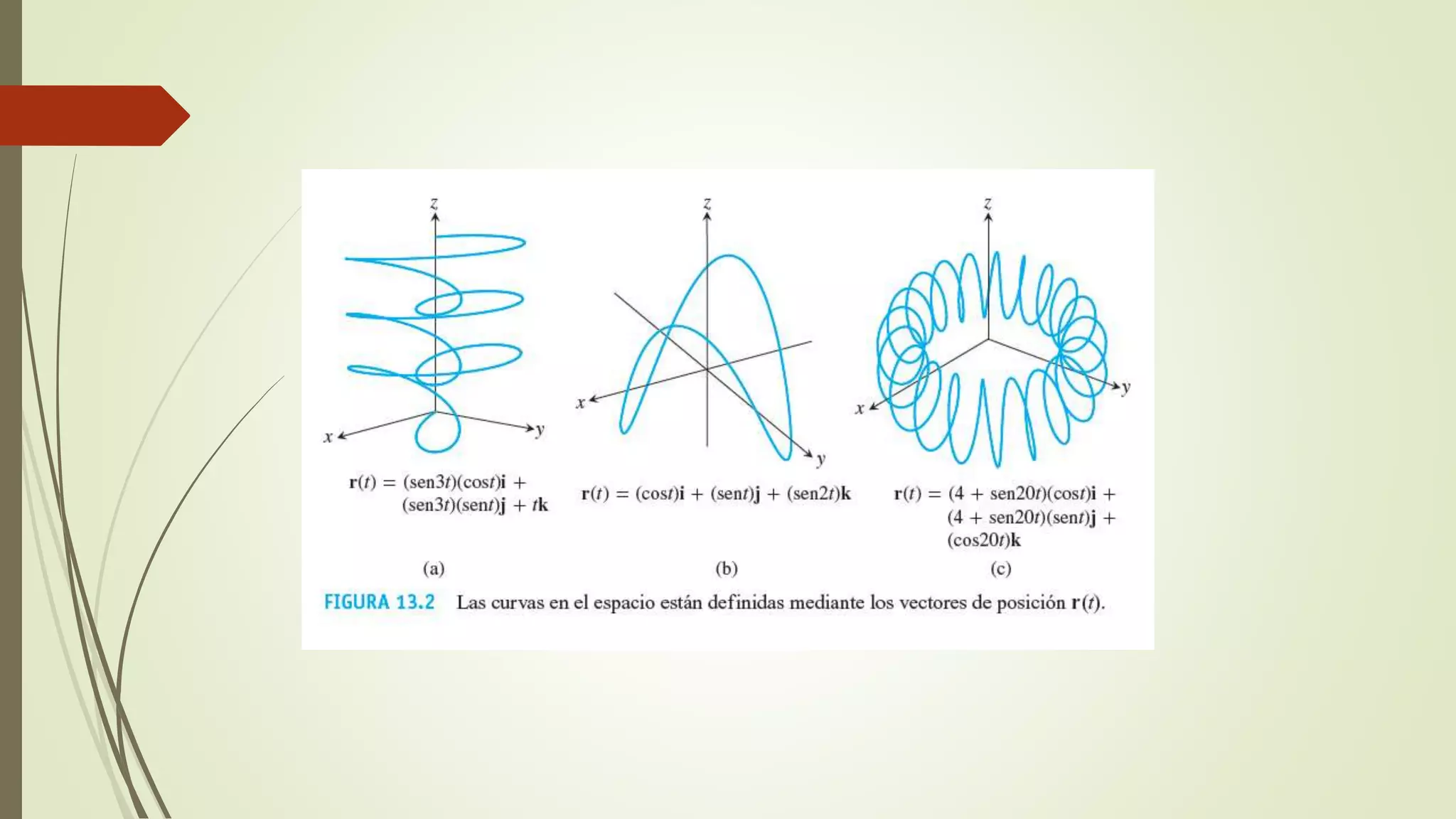
Las funciones vectoriales son funciones matemáticas cuyo dominio es un conjunto de números reales y cuyo rango es un conjunto infinito de vectores. Una función vectorial puede tomar valores escalares o vectoriales como entrada y siempre devuelve una cantidad vectorial. El rango de una función vectorial puede dividirse en componentes constitutivas y el dominio es la intersección de los dominios de estas funciones.