Descargar para leer sin conexión
Subido poraz0dj96
PPTX, PDF91 vistas
Rectas y planos
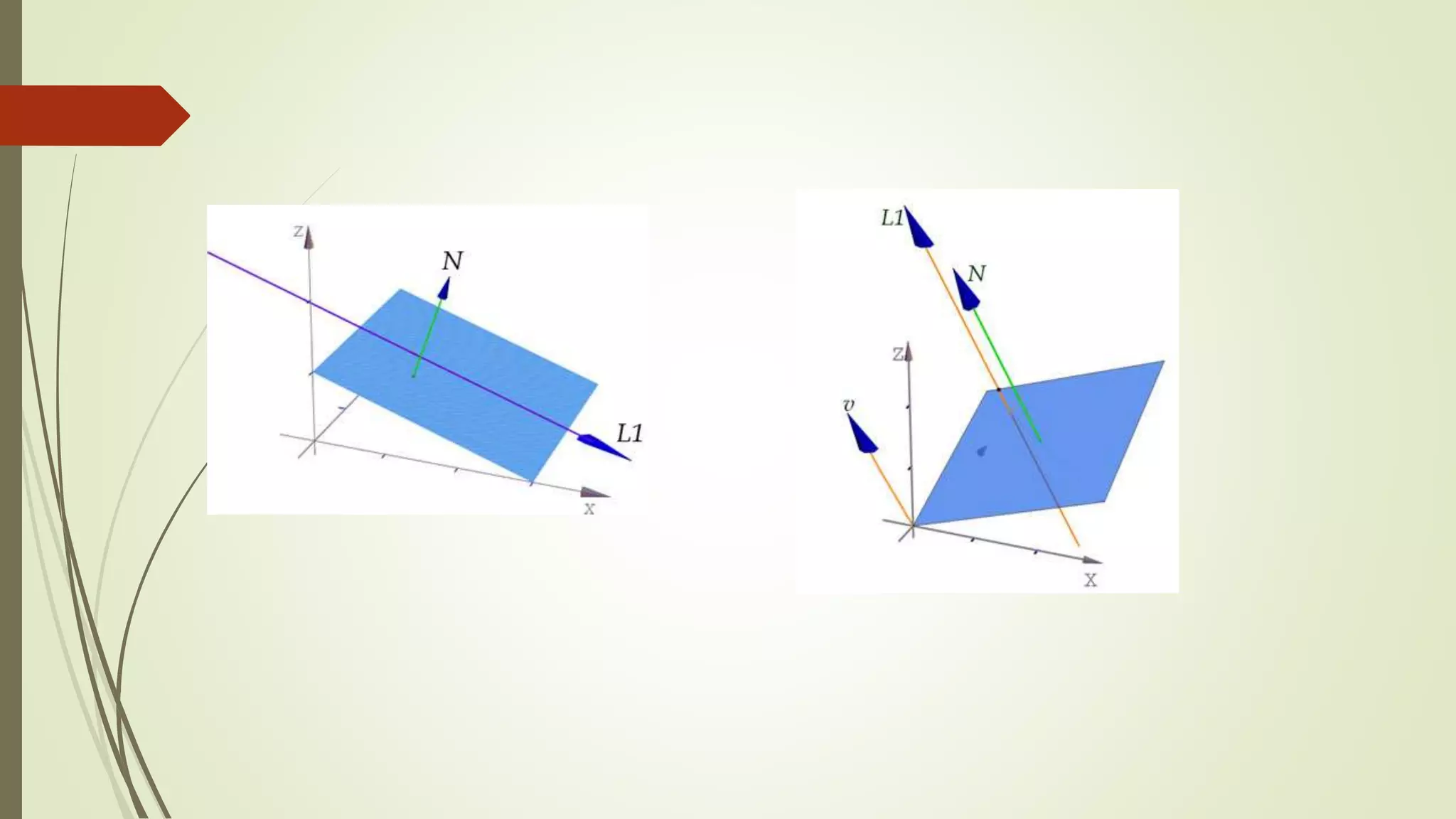
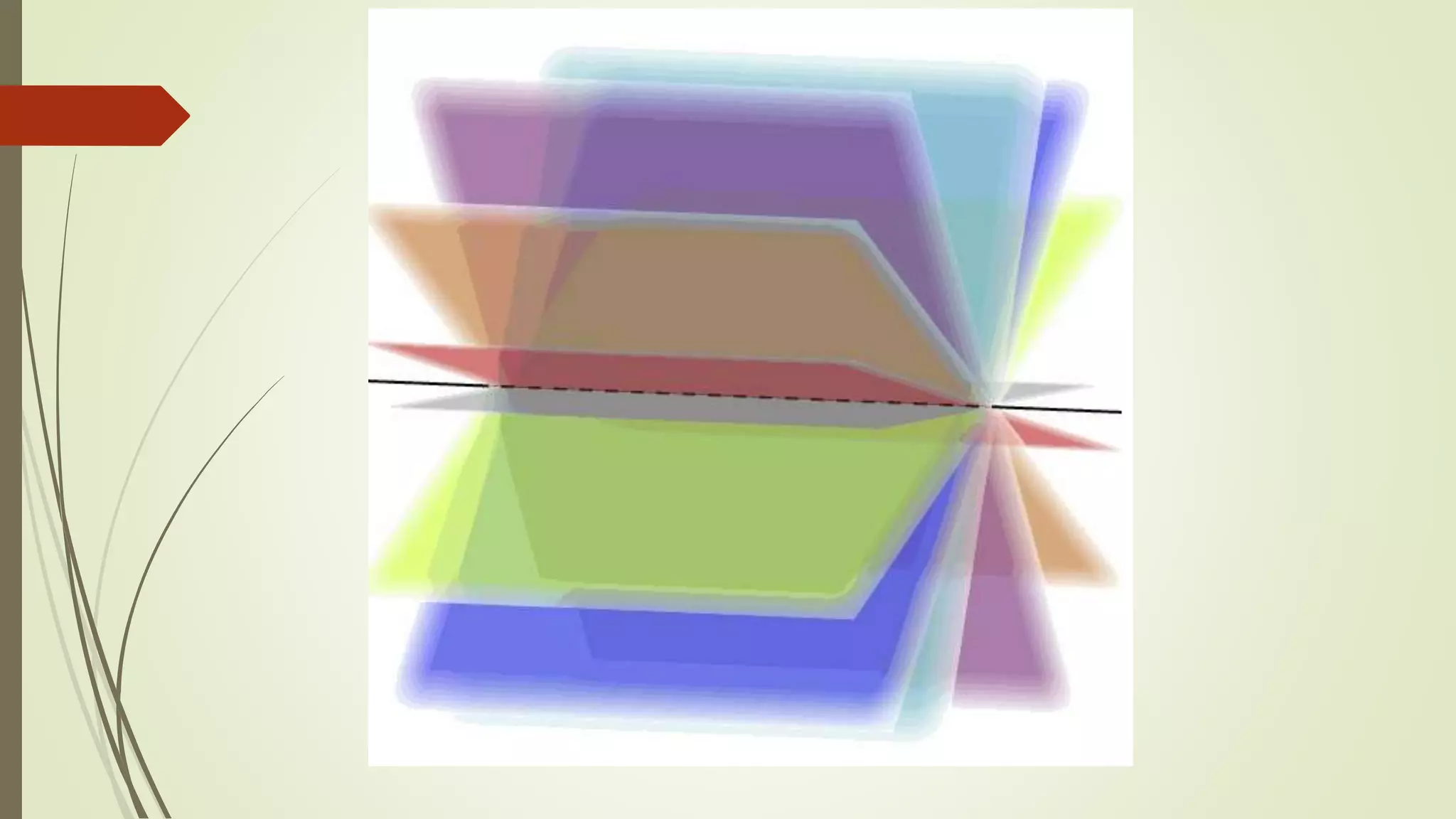
Este documento describe cómo determinar una recta a partir de dos planos y cómo calcular la distancia entre un punto y esa recta. Explica que el vector director de la recta es el producto vectorial de los vectores normales de los dos planos. También proporciona las ecuaciones paramétricas y canónicas de la recta, así como la definición de un haz de planos que pasan por la recta.
Más contenido relacionado
La actualidad más candente
Destacado
Rectas y planos
- 3. Recta determinada pordos planos Vector director de la recta L 𝑎 = 𝑛1 × 𝑛2 = 𝑙, 𝑚, 𝑛 𝑎 = 𝑖 𝑗 𝑘 𝐴1 𝐵1 𝐶1 𝐴2 𝐵2 𝐶2 = 𝐵1 𝐶1 𝐵2 𝐶2 𝑖 + 𝐶1 𝐴1 𝐶2 𝐴2 𝑗 + 𝐴1 𝐵1 𝐴2 𝐵2 𝑘 Un punto sobre la recta L 𝑆𝑖 𝑦 = 0 𝐴1 𝑥 + 𝐶1 𝑧 + 𝐷1 = 0 𝐴2 𝑥 + 𝐶2 𝑧 + 𝐷1 = 0 𝑃1 = 𝑥1, 0, 𝑧1 𝑟1 = 𝑥1, 0, 𝑧1 𝑟 = 𝑟1 + 𝑡 𝑎 = 𝑥1, 0, 𝑧1 + 𝑡 𝐵1 𝐶1 𝐵2 𝐶2
- 4. Ecuaciones paramétricas 𝑥 =𝑥1 + 𝑡 𝐵1 𝐶1 𝐵2 𝐶2 𝑦 = 0 + 𝑡 𝐶1 𝐴1 𝐶2 𝐴2 𝑧 = 𝑧1 + 𝑡 𝐴1 𝐵1 𝐴2 𝐵2 Ecuaciones canónicas 𝑥 − 𝑥1 𝐵1 𝐶1 𝐵2 𝐶2 = 𝑦 − 0 𝐶1 𝐴1 𝐶2 𝐴2 = 𝑧 − 𝑧1 𝐴1 𝐵1 𝐴2 𝐵2
- 6. Haz de planos Conjuntoinfinito de planos que pasan por una misma recta 0 = 𝐴1 + 𝜆𝐴2 𝑥 + 𝐵1 + 𝜆𝐵2 𝑦 + 𝐶1 + 𝜆𝐶2 𝑧 + 𝐷1 + 𝜆𝐷2 𝑛 = 𝐴1 + 𝜆𝐴2, 𝐵1 + 𝜆𝐵2, 𝐶1 + 𝜆𝐶2 Donde 𝜆 = 𝛽 𝛼 𝑦 𝛼 ≠ 0, tal que 𝛼, 𝛽𝜖ℝ − 0
- 7. Distancia de unpunto a la recta L 𝑑 = 𝑎 × 𝑟1 − 𝑟0 𝑎