VECTORIALES

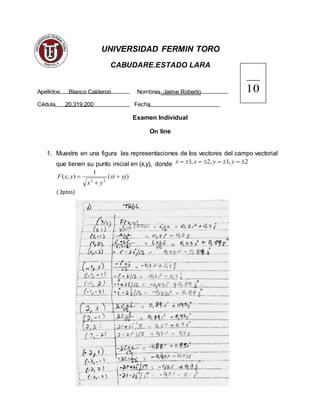
1. UNIVERSIDAD FERMIN TORO
CABUDARE.ESTADO LARA
Apellidos Blanco Calderon Nombres Jaime Roberto
Cédula 20.319.200 Fecha
Examen Individual
On line
1. Muestre en una figura las representaciones de los vectores del campo vectorial
que tienen su punto inicial en (x,y), donde 2,1,2,1  yyxx
)(
1
),(
22
yjxi
yx
yxF 


( 2ptos)
10

2. 2. Calcule )()( tRytR  si tkjtittR  11)( 22
si k
t
t
tji
t
tR
1
tan
1
1
)( 2



 y kjiR 534)0(  calcule R(t) ( 2ptos)
tkjtittR  11)( 22
    tkjtittR 
2/122/12
11)(
    ktttittR 

2.1
2
1
21
2
1
)('
2/122/12
kj
t
t
i
t
tR 




11
1
)('
22

3.         jttttitttttR 













2.1
2
1
.12.1
2
1
.1)(''
2/322/122/322/12
   
j
t
t
t
i
t
t
t
tR
























32
2
232
2
2
11
1
11
1
)(''
Si 1
tan
1
1
)(' 2




t
tk
tji
t
tR y kjioR 534)(' 
  



1
tan
1
)(' 2
t
tk
tji
t
dt
tR
ktLn
t
dt

 /1/
1
   ktLndt
t
sent
dt /sec/
cos
tan
dt
t
t
 1
KLnU
U
du
 2
1
2
1
tktLn
t
tdt
/1/
2
1
1
2
2


dtdu
tU


2
12
tdt
du

2
CktLnjtLnitLntR  /1/
2
1
/sec//1/)( 2
CKLnjOLniLnoR  /10/
2
1
/sec/)10()( 2
kjiC 534  CoR )(

4.     K
t
t
jtLnitLntR 





 5
1
3)sec/4/1/)( 2
3. Calcule el rot F y div R para el campo vectorial F dado
kj
yx
y
i
yx
x
zyxF 




2
3
222
3
22
)()(
),,( ( 2ptos)
1
)()( 2/32222
2
yx
y
yx
x
d
d
dy
d
dx
d
kji
tFro


   2/322
22
2/3222/322
2
1
)()( yx
y
dy
d
j
yx
x
dx
d
i
yx
y
yx
x
d
d
dy
d
dx
d
kji
tFro


      






























 ko
yx
x
dy
d
yx
y
dz
d
j
dx
d
k
yx
y
dx
d
j
yx
x
dz
d
i
dy
d
tFr 2/3222/3222/3222/322 )(
11
   
k
yx
x
dy
d
k
yx
y
dx
d
tFro



















 2/3222/322
    kyxx
dy
d
kyxy
dx
d
tFro
2/3222/322
.. 
    ykyxxxkyxytFro 2.
2
3
2.
2
3 2/1222/122

kyxxykyxxytFro
2222
33 
0tFro

5.  
k
dz
d
yx
y
dy
d
yx
x
dx
d
divR 
















 2/3222/322 )(
   
  
   
  22/322
2/1222/322
22/322
2/1222/322
2.2/3.2.2/3.
yx
yyxyyx
yx
xyxxyx
divR






   
 
   
 322
2/1222/322
322
2/12222/322
33
yx
yxyyx
yx
yxxyx
divR






   
 322
2222222/122
33
yx
yyxxyxyx
divR



   
 322
222/122
yx
yxyx
divR



   
 322
222/122
yx
yxyx
divR



 
 322
2/322
yx
yx
divR



  2/322
1
yx
divR



4. Obtenga una ecuación del plano tangente al paraboloide elíptico
(2,4,2)puntoelen0164 22
 zyx ( 2 ptos)
Una ecuación del plano tangente es
         Uzzzyxfyyzyxfyxxzyxfx oooooooooo  ,200 ,,,.,,

6.       kzzjyyixxzyxF oooo  .,, 00
ó
       kzzjyyixxzyyF ooo  ,,1
  kyjxiF 16282,4,2 
  kjiF 164162,4,2 
Entonces la ecuación del plano tangente es
      021648216  zyxk
032163283216  zyx
03216816  zyx diventre 8
0422  zyx
5. Obtenga una ecuación de la recta normal a la superficie en el punto indicado.
)1,27,8(;143
2
3
2
3
2
 zyx ( 2ptos)
   1,27,8;14,, 3/23/23/2
 zyxzyxf
  kyjyixzyxf 3/13/13/1
3
2
3
2
3
2
,,  
  k
z
j
y
i
x
zyxf 333
3
2
3
2
3
2
,, 


 
 
kjif 333 13
2
273
2
83
2
1,27,8 


  kjif
3
2
9
2
3
1
1,27,8 



7. Las ecuaciones simétricasparala rectanormal son:
3/2
1
9/2
27
3/1
8 




 zyx