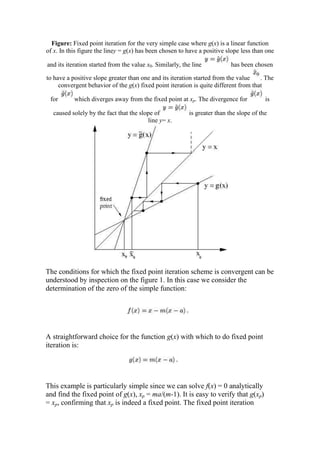
Fixedpoint
- 1. Figure: Fixed point iteration for the very simple case where g(x) is a linear function of x. In this figure the liney = g(x) has been chosen to have a positive slope less than one and its iteration started from the value x0. Similarly, the line has been chosen to have a positive slope greater than one and its iteration started from the value . The convergent behavior of the g(x) fixed point iteration is quite different from that for which diverges away from the fixed point at xp. The divergence for is caused solely by the fact that the slope of is greater than the slope of the line y= x.<br />The conditions for which the fixed point iteration scheme is convergent can be understood by inspection on the figure 1. In this case we consider the determination of the zero of the simple function: <br />A straightforward choice for the function g(x) with which to do fixed point iteration is: <br />This example is particularly simple since we can solve f(x) = 0 analytically and find the fixed point of g(x), xp = ma/(m-1). It is easy to verify that g(xp) = xp, confirming that xp is indeed a fixed point. The fixed point iteration sequence is shown for two choices of the slope, m, both positive. The curve y = g(x) has m < 1 and the curve has m > 1. It is clear that the m < 1 case results in monotonic convergence to the fixed point xp, so that the fixed point is strongly attractive in this case. The m > 1 case illustrates monotonic divergence away from the fixed point xp, so that the fixed point is strongly repellent in this case.<br />While this simple linear case may seem special, it displays the behaviour which applies in general to a continuous mapping function, g(x). In order to understand the reasons for the difference in behaviour for the two cases m < 1 and m > 1, we need to follow the iteration sequence in some detail. Once given the starting value x0, we compute g(x0), the corresponding point on the y = g(x) curve. We then move along the line to intersect the y = x line, and there read the value ofx, and use this as the next iteration value for x. Examination of the m < 1 iteration sequence in the figure shows that each motion along the arrows of the iteration sequence leads towards the intersection point of y = x and y = g(x), thus assuring convergence. A similar examination of the m > 1 case shows that each motion along the arrows of the iteration sequence leads away from the intersection point at xp, thus assuring divergence. While the point xp remains a fixed point of , it is an unstable fixed point in the sense that starting arbitrarily close to the fixed point still results in an iterative path that leads away from the fixed point. The termsattractor and repeller then naturally describe the fixed point xp for the maps associated with m < 1 and m > 1 respectively.<br />Figure 6.3: Fixed point iteration for a general function g(x) for the four cases of interest. Generalizations of the two cases of positive slope shown in the figure 1 are shown on the left, and illustrate monotonic convergence and divergence. The cases where g(x) has negative slope are shown on the right, and illustrate oscillating convergence and divergence. The top pair of panels illustrate strong and weak attractors, while the bottom pair of panels illustrate strong and weak repellers.<br />We have considered iteration functions, like g(x), which have positive slopes in the neighborhood of the fixed point, and shown that these lead to either monotonic convergence or monotonic divergence. When g(x) has negative slope in the neighborhood of the fixed point, the result is oscillating convergence or divergence, with convergence requiring |m| < 1. The iteration sequences for all four cases are shown in the figure 1 for more general g(x). The conditions leading to convergence are unchanged from those derived for the linear case as long as the neighborhood of the fixed point considered is small enough.<br />