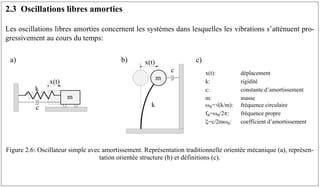
1. 2.3 Oscillations libres amorties
Les oscillations libres amorties concernent les systèmes dans lesquelles les vibrations s’atténuent pro-
gressivement au cours du temps:
Figure 2.6: Oscillateur simple avec amortissement. Représentation traditionnelle orientée mécanique (a), représen-
tation orientée structure (b) et définitions (c).
x(t): déplacement
k: rigidité
c: constante d’amortissement
m: masse
ωn=√(k/m): fréquence circulaire
fn=ωn/2: fréquence propre
ζ=c/2mωn: coefficient d’amortissement
m
k
c
x(t)
m
k
x(t)
c
a) b) c)

2. 2.3.1 Equation différentielle
L’équation différentielle s’établit à partir des forces agissant sur la masse.
Conformément à la deuxième loi de Newton, l’équation du mouvement s’exprime:
(2.9)
après division par m, et en posant ζ=c/(2mωn), on obtient l’expression épurée suivante:
(2.10)
Figure 2.7: Forces agissant sur la masse pour un oscillateur simple avec amortissement.
m
k·x(t)
x(t)
c·x(t)
.
x(t)
m
k·x(t)
c·x(t)
.
a) b)
m x
··
⋅ c x
·
⋅ k x
⋅
+ + 0
=
x
·· 2ζωn x
·
⋅ ωn
2
x
⋅
+ + 0
=

3. 2.3.3 Résolution
La solution est de la forme . Pour le paramètre (r), l’équation caractéristique associée est:
. Il y a alors deux solutions pour r:
La solution générale est composée de la somme de deux termes correspondants:
avec C1 et C2: constantes (2.11)
Selon la valeur du paramètre ζ, trois cas d’amortissement différents doivent être distingués:
1) amortissement faible: ζ1
2) amortissement fort: ζ1
3) amortissement critique: ζ=1
x t
( ) A e
rt
⋅
=
r
2
2ζωn r ωn
2
+
⋅
+ 0
=
r1 ζωn
( )
– ζωn
( )
2
ωn
2
–
+
= r2 ζωn
( )
– ζωn
( )
2
ωn
2
–
–
=
x t
( ) C1 e
r1t
⋅ C2 e
r2t
⋅
+
=

4. Figure 2.8: Selon la valeur du paramètre ζ, les oscillations peuvent être de type amortissement faible (ζ1), amor-
tissement fort (ζ1) ou bien amortissement critique (ζ=1).
0 0.5 1 1.5 2 2.5 3 3.5
t/Tn
-1
-0.5
0
0.5
1
x(t)/X
0 z= 0.1
z= 1
z= 3
ζ=0.1
ζ=1.0
ζ=3.0

5. 2.3.4 Amortissement faible: ζ1
Dans ce cas, les racines r1 et r2 sont complexes car le terme ((ζωn)2-ωn2) est négatif. En posant:
les racines r1 et r2 peuvent s’écrire de la façon suivante:
La solution générale s’écrit alors:
(2.12)
Les termes C1+C2 et (C1-C2)·i peuvent être remplacés par les constantes C=C1+C2 et D=(C1-C2)·i.
(2.13)
Les constantes C et D sont déterminées par les conditions initiales.
ωD ωn
2
ζωn
( )
2
–
=
r1 ζωn
( )
– iωD
+
= r2 ζωn
( )
– iωD
–
=
x t
( ) C1 e
ζωn
( )
– iωD
+
( )t
⋅ C2 e
ζωn
( )
– iωD
–
( )t
⋅
+
= =
x t
( ) e
ζωnt
–
C1 C2
+
( ) ωDt
cos
⋅ C1 C2
–
( ) i ωD
sin t
⋅ ⋅
+
[ ]
⋅
=
x t
( ) e
ζωnt
–
C ωDt
cos
⋅ D ωD
sin t
⋅
+
( )
⋅
=

6. La pseudo-pulsation (ωD) est définie à partir de ωn et de ζ par: .
Solutions en fonction des conditions initiales (X0 et V0 en t=0)
En t=0, le terme du sinus disparaît et le terme du cosinus prend une valeur unitaire. Par conséquent, la
valeur de la constante C est égale au déplacement initial (X0):
L’expression de la vitesse s’obtient par la dérivée de l’équation (2.13):
(2.14)
En t=0, les termes en sinus disparaissent et les termes en cosinus prennent une valeur unitaire. La cons-
tante D s’exprime alors:
ωD ωn
2
ζωn
( )
2
– ωn 1 ζ
2
–
⋅
= =
C X0
=
x
· t
( ) ζωne
–
ζωnt
–
C ωDt
cos
⋅ D ωD
sin t
⋅
+
( ) e
ζωnt
–
D ωD ωDt
cos
⋅ ⋅ C
– ωD ωDt
sin
⋅ ⋅
( )
+
=
V0 ζωn
– C
( )
⋅ D ωD
⋅
+ ζωn
– X0
⋅ D ωD
⋅
+ D
V0 ζωnX0
+
ωD
------------------------------
-
=
⇒
= =

7. La prise en compte des conditions initiales conduit donc à l’expression suivante:
(2.15)
La solution générale peut également être exprimée par une formulation alternative avec un cosinus:
(2.16)
x t
( ) e
ζωnt
–
X0 ωDt
cos
⋅
V0 ζωnX0
+
ωD
------------------------------
- ωD
sin t
⋅
+
⎝ ⎠
⎜ ⎟
⎛ ⎞
⋅
=
x t
( ) X0
2 V0 ζωnX0
+
ωD
------------------------------
-
⎝ ⎠
⎜ ⎟
⎛ ⎞2
+ e
ζωnt
–
ωDt
V0 ζωnX0
+
ωDX0
------------------------------
-
⎝ ⎠
⎜ ⎟
⎛ ⎞
atan
–
⎝ ⎠
⎜ ⎟
⎛ ⎞
cos
⋅ ⋅
=

8. Figure 2.9: Les oscillations amorties sont caractérisées par un déplacement se répétant indéfiniment avec une
pseudo-période TD=2π/ωD, mais s’atténuant progressivement selon une enveloppe exponentielle (a). L’amortisse-
ment tend à allonger faiblement la période des oscillations par rapport à celle des oscillations non amorties (b).
0 0.5 1 1.5 2 2.5 3
t/Tn
-1
-0.5
0
0.5
1
x(t)/X
0
TD
TD
0 0.5 1 1.5 2 2.5 3
t/Tn
-1
-0.5
0
0.5
1
x(t)/X
0
Tn
TD
a) b)
e−ζωnt

9. Figure 2.10: Le coefficient d’amortissement (ζ) décrit la rapidité d’atténuation de l’amplitude des oscillations.
0 1 2 3 4 5 6 7
-1
-0.5
0
0.5
1
x(t)/X
0
0 1 2 3 4 5 6 7
-1
-0.5
0
0.5
1
x(t)/X
0
0 1 2 3 4 5 6 7
t/Tn
-1
-0.5
0
0.5
1
x(t)/X
0
0 1 2 3 4 5 6 7
t/Tn
-1
-0.5
0
0.5
1
x(t)/X
0
ζ = 0.02 ζ = 0.05
ζ = 0.10 ζ = 0.20

10. 2.3.5 Décrément logarithmique
En prenant deux maxima successifs (xr et xq) des oscillations (espacés d’une pseudo-période, TD):
et
Figure 2.11: Le décrément logarithmique permet l’estimation du coefficient d’amortissement.
0 0.5 1 1.5 2 2.5 3
t/Tn
-2
-1
0
1
2
x(t)/X
0
TD
x
r
x
q
0 1 2 3 4 5
t/Tn
-2
-1
0
1
2
x(t)/X
0
4T
D
x
r
x
s
a) b)
xr A e
ζωnt
–
⋅
= xq A e
ζωn t TD
+
( )
–
⋅ A e
ζωn t
2π
ωD
------
-
+
⎝ ⎠
⎛ ⎞
–
⋅
= =

11. Le décrément logarithmique (Δ) est le logarithme du rapport de ces deux maxima:
L’approximation d’un amortissement faible ( ) permet l’estimation du coefficient d’amortisse-
ment (ζ).
La généralisation où les maxima sont séparés par plus d’une pseudo-période (n·TD) est immédiate et on
obtient: .
Cette dernière relation peut être inversée pour extraire le nombre d’oscillations (n50%) nécessaires pour
réduire l’amplitude de moitié: .
Pour un amortissement de ζ=5%, il faut 2.2 cycles pour diminuer l’amplitude de moitié.
Δ Log
xr
xq
-----
⎝ ⎠
⎜ ⎟
⎛ ⎞ 2πζωn
ωD
----------------
- 2πζ
≈
= = ζ
Δ
2π
-----
-
≈
⇒
ωD ωn
≈
ζ Δ 2πn
( )
⁄
≈
n50% Log2 2πζ
( )
⁄ 11 ζ %
[ ]
⁄
≅
=

12. 2.3.6 Amortissement fort: ζ1
Dans ce cas les racines r1 et r2 sont réelles car le terme ((ζωn)2-ωn2) est positif. En posant:
les racines r1 et r2 peuvent s’écrire de la façon suivante:
En prenant en compte les conditions initiales (X0 et V0 en t=0), on obtient l’expression:
(2.19)
La formulation est similaire à celle de l’équation (2.15), sauf que les fonctions trigonométriques ont été
remplacées par leurs analogues hyperboliques. D’un point de vue dynamique, il n’y a pas de vibrations,
le système s’approche lentement de sa position d’équilibre.
ω̂D ωn ζ
2
1
–
⋅
=
r1 ζωn
( )
– ω̂D
+
= r2 ζωn
( )
– ω̂D
–
=
x t
( ) e
ζωnt
–
X0 ω̂Dt
cosh
⋅
V0 ζωnX0
+
ω̂D
------------------------------
- ω̂D
sinh t
⋅
+
⎝ ⎠
⎜ ⎟
⎛ ⎞
⋅
=

13. 2.3.7 Amortissement critique: ζ=1
Dans ce cas les racines r1 et r2 sont réelles et égales (r1=r2=-ωn), car le terme ((ζωn)2-ωn2) est nul. La
solution générale s’écrit alors:
(2.20)
Avec les conditions initiales (X0 et V0 en t=0), on obtient l’expression:
(2.21)
Comme dans le cas de l’amortissement fort, il n’y a pas de vibrations, mais le système s’approche rapi-
dement de sa position d’équilibre.
x t
( ) e
ωnt
–
C1 C2 t
⋅
+
( )
⋅
=
x t
( ) e
ωnt
–
X0 V0 ωnX0
+
( ) t
⋅
+
[ ]
⋅
=

14. 2.4 Oscillations entretenues (ou forcées)
Les oscillations entretenues concernent les systèmes dans lesquelles les vibrations sont engendrées par
une force extérieure harmonique.
Figure 2.13: Oscillateur simple amorti soumis à une force harmonique. Représentation mécanique (a), représenta-
tion orientée structure (b) et définitions (c).
m
k
x(t)
c
F0·sinωt
m
k
c
x(t)
F0·sinωt
x(t): déplacement
k: rigidité
c: constante d’amortissement
m: masse
ωn=√(k/m): fréquence circulaire
fn=ωn/2: fréquence propre
ζ=c/2mωn: coefficient d’amortissement
ω: pulsation de la force harmonique
F0: amplitude de la force harmonique
a) b) c)

15. 2.4.1 Equation différentielle
L’équation différentielle s’établit à partir des forces agissant sur la masse.
Suivant la deuxième loi de Newton, l’équation du mouvement s’exprime:
(2.22)
après division par m, on obtient l’expression épurée suivante:
(2.23)
Figure 2.14: Forces agissant sur la masse pour un oscillateur simple amorti soumis à une force harmonique.
m
k·x(t)
x(t)
c·x(t)
.
F0·sinωt
x(t)
m
k·x(t)
c·x(t)
.
F0·sinωt
a) b)
m x
··
⋅ c x
·
⋅ k x
⋅
+ + F0 ωt
sin
⋅
=
x
·· 2ζωn x
·
⋅ ωn
2
x
⋅
+ + F0 m
⁄ ωt
sin
⋅
=

16. 2.4.2 Résolution
La solution générale, somme: solution homogène (xh) + solution particulière (xp): .
La solution homogène s’exprime de la manière suivante:
La solution particulière est de la forme:
La solution générale s’exprime:
(2.24)
x t
( ) xh t
( ) xp t
( )
+
=
xh t
( ) C e
ζωnt
–
ωDt φ1
–
( )
cos
⋅ ⋅
=
xp t
( ) D ωt φ2
–
( )
sin
⋅
=
x t
( ) C e
⋅
ζωnt
–
ωDt φ1
–
( )
cos
⋅
F0
k
-----
-
1
ω
2
ωn
2
------
–
⎝ ⎠
⎜ ⎟
⎛ ⎞2
4 ζ
2 ω
ωn
------
⎝ ⎠
⎛ ⎞
2
⋅ ⋅
+
-------------------------------------------------------------------
- ωt
2ζωnω
ωn
2
ω
2
–
-------------------
⎝ ⎠
⎜ ⎟
⎛ ⎞
atan
–
⎝ ⎠
⎜ ⎟
⎛ ⎞
sin
⋅
+
=

17. On détermine les constantes C et φ1 avec les conditions initiales (généralement X0=0 et V0=0 en t=0).
La réponse totale de l’oscillateur simple est composée de deux sinusoïdes oscillant à des fréquences dis-
tinctes: une sinusoïde de base (à l’équilibre) à la fréquence de la force perturbatrice à laquelle s’ajoute
une sinusoïde à la fréquence propre de l’oscillateur. La sinusoïde de base (à l’équilibre) correspond à la
solution particulière (xp) et la sinusoïde à la fréquence propre de l’oscillateur correspond à la solution
homogène (xh). L’amortissement (même faible) a pour effet de faire disparaître la solution homogène
après quelques oscillations alors que cette solution persiste indéfiniment en absence d’amortissement.
Pour des raisons didactiques, les graphiques sont souvent tracés pour une vitesse initiale importante afin
de bien mettre en évidence les deux sinusoïdes dont la réponse totale est composée. Avec une vitesse
initiale nulle (V0=0 en t=0) l’effet est moins spectaculaire. Ce cas est toutefois plus réaliste et il montre
que la différence entre réponse totale et réponse à l’équilibre n’est généralement pas aussi importante,
même sans amortissement.

18. Figure 2.15: La réponse totale se compose de deux sinusoïdes avec des fréquences différentes.
0 0.5 1 1.5 2 2.5
t/T
-2
-1
0
1
2
F(t)/F
0
F0
-F
0
0 0.5 1 1.5 2 2.5
t/T
-2
-1
0
1
2
F(t)/F
0
F0
-F
0
0 0.5 1 1.5 2 2.5
t/T
-2
-1
0
1
2
x(t)/d
s
tat
0 0.5 1 1.5 2 2.5
t/T
-2
-1
0
1
2
x(t)/d
s
tat
totale
équilibre
a) b)
x(t)/δ
stat
x(t)/δ
stat

19. Figure 2.16: Avec V0 = 0, la réponse totale s’éloigne peu de la réponse à l’équilibre, même sans amortissement.
0 0.5 1 1.5 2 2.5
t/T
-2
-1
0
1
2
F(t)/F
0
F
0
-F
0
0 0.5 1 1.5 2 2.5
t/T
-2
-1
0
1
2
F(t)/F
0
F
0
-F
0
0 0.5 1 1.5 2 2.5
t/T
-2
-1
0
1
2
x(t)/d
s
tat
0 0.5 1 1.5 2 2.5
t/T
-2
-1
0
1
2
x(t)/d
s
tat
totale
équilibre
a) b)
x(t)/δ
stat
x(t)/δ
stat

20. Le premier terme de la solution générale représente la solution homogène qui disparaît après quelques
oscillations amorties. Le deuxième terme persiste indéfiniment et représente la solution particulière à la
fréquence de la force perturbatrice. La fraction devant le sinus correspond à l’amplification dynamique
de la force F0.
Rd est le facteur d’amplification dynamique de l’application harmonique de la force F0 à la pulsation ω:
(2.25)
Sans amortissement, Rd tend vers l’infini pour ω/ωn=1. C’est la résonance. Avec amortissement, les
déplacements ne sont plus infinis et Rd vaut Rd=1/(2ζ) pour ω/ωn=1. Le pic du facteur d’amplification
apparaît cependant pour un rapport des fréquences un peu plus petit, mais proche de l’unité:
Rd
1
1
ω
2
ωn
2
------
–
⎝ ⎠
⎜ ⎟
⎛ ⎞2
4 ζ
2 ω
ωn
------
⎝ ⎠
⎛ ⎞
2
⋅ ⋅
+
-------------------------------------------------------------------
-
=
Rd max
,
1
2ζ 1 ζ
2
–
⋅
-----------------------------
=
ω
ωn
------ 1 2ζ
2
–
=

21. Figure 2.17: Facteur d’amplification dynamique (Rd) en fonction du rapport de la fréquence de la force perturba-
trice et de la fréquence propre de la structure; sans amortissement (a) et avec amortissement (b).
0 0.5 1 1.5 2 2.5 3 3.5
w/wn
0
1
2
3
4
5
R
d
0 0.5 1 1.5 2 2.5 3 3.5
w/wn
0
1
2
3
4
5
R
d
z= 0.01
z= 0.1
z= 0.2
z= 0.7
z= 1
a) b)
ζ=0.01
ζ=0.10
ζ=0.20
ζ=0.70
ζ=1.00
ω/ωn
ζ = 0
ω/ωn

22. 0 0.5 1 1.5 2 2.5
-3
-2
-1
0
1
2
3
x(t)/d
s
tat R
d
=1.29
réponse
excitation
0 0.5 1 1.5 2 2.5
-3
-2
-1
0
1
2
3
x(t)/d
s
tat
Rd
=2.5
0 0.5 1 1.5 2 2.5
t/T
-3
-2
-1
0
1
2
3
x(t)/d
s
tat
R
d
=1.0
réponse
excitation
0 0.5 1 1.5 2 2.5
t/T
-3
-2
-1
0
1
2
3
x(t)/d
s
tat
R
d
=0.32
réponse
excitation
ω/ωn=0.5 ω/ωn=1.0
ω/ωn=1.356 ω/ωn=2.0
x(t)/δ
stat
x(t)/δ
stat
x(t)/δ
stat
x(t)/δ
stat

23. 2.4.4 Résonance
Le phénomène de résonance apparaît lorsque les fréquences coïncident (ω=ωn).
Figure 2.19: La résonance apparaît lorsqu’un oscillateur non amorti est soumis à une force harmonique variant à une
fréquence égale à la fréquence propre de celui-ci. A chaque cycle, l’amplitude des déplacements augmente réguliè-
rement d’un incrément de 2·π·δstat (a). En présence d’amortissement, l’augmentation est bornée (b).
0 2 4 6 8 10 12
t/Tn
-40
-20
0
20
40
x(t)/d
s
tat
0 2 4 6 8 10 12
t/Tn
-20
-10
0
10
20
x(t)/d
s
tat
x(t)/δ
stat
a) b)
π
π
x(t)/δ
stat
1/2ζ
1/2ζ

24. Sans amortissement:
(2.26)
Avec amortissement:
(2.27)
Cette équation se simplifie si l’on considère un amortissement faible, car le terme en sinus peut être
négligé. Par ailleurs, les fréquences sont proches ( ). On obtient:
Les oscillations se développent avec le temps selon un cosinus dont l’amplitude est modulée par une
enveloppe de type exponentiel. Le déplacement maximum n’est pas infini. Il est borné par un facteur
qui est en fonction inverse de l’amortissement.
x t
( )
F0
2k
-----
- ωnt ωnt ωnt
cos
⋅
–
sin
( )
⋅
δstat
2
----------
- ωnt ωnt ωnt
cos
⋅
–
sin
( )
⋅
= =
x t
( )
δstat
2ζ
----------
- e
ζωnt
–
ωDt
ζ
1 ζ
2
–
------------------
- ωDt
sin
⋅
+
cos
⎝ ⎠
⎜ ⎟
⎛ ⎞
⋅ ωnt
cos
–
⋅
=
ωD ωn
≈
x t
( )
δstat
2ζ
----------
- e
ζωnt
–
1
–
⎝ ⎠
⎛ ⎞ ωnt
cos
⋅
⋅
≅