Capitulo4 deflexaode vigas

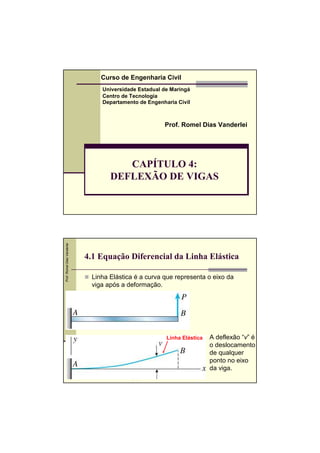
Curso de Engenharia Civil
Universidade Estadual de Maringá
Centro de Tecnologia
Departamento de Engenharia Civil

Prof. Romel Dias Vanderlei

CAPÍTULO 4:
DEFLEXÃO DE VIGAS

4.1 Equação Diferencial da Linha Elástica

Linha Elástica é a curva que representa o eixo da
viga após a deformação.

Linha Elástica A deflexão “v” é
o deslocamento
de qualquer
ponto no eixo
da viga.



Quando a viga é flexionada, ocorrem em cada ponto
ao longo do eixo uma deflexão (v) e uma rotação (θ).
O ângulo de rotação “θ” é o ângulo entre o eixo “x” e
a tangente à curva da linha elástica.

θ
dθ
θ
dθ


Da figura vemos que:

ρ .d θ = ds
θ
dθ

1 dθ
k= =
ρ ds

dθ em radianos



Da figura vemos que:
dv
= tg θ
θ
dθ dx
Inclinação da Linha Elástica

 dv 
θ = arctg 
 dx 
 dx
 cos θ =
 ds
e: 
 sen θ = dv

 ds


Vigas com Pequenos Ângulos de Rotação: θ 0
1 dθ
ds ≈ dx → k = =
ρ dx
dv
tgθ ≈ θ → = θ , sendo θ em radianos.
dx
Logo, fazendo: dθ = d v
2

dx dx2
1 d 2 v Equação válida para
k= =
ρ dx 2 pequenas rotações



Para materiais elástico lineares (Lei de Hooke):
1
σ x = E⋅ ε x e εx = ⋅y=k⋅y
ρ
∫σ
A
x ⋅ dA ⋅ y = M → ∫ E ⋅ ( k ⋅ y ) ⋅ y ⋅ dA = M
A

M
E ⋅ k ∫ y 2 ⋅ dA = M → E ⋅ k ⋅ I z = M → k =
A
E ⋅ Iz

d 2v M Equação Diferencial da
Logo: = Linha Elástica
dx 2 EI z


Convenções de Sinais:
y(+)
(1)Eixos:
x(+)

(2) Deflexão: v(+)
y
dv
(3) Rotações: e θ (+)
dx x

(4) Curvatura k:



Convenções de Sinais:

(5) Momentos:

(6) Carregamentos:


Equações Adicionais:

dM dV d 2M
=V ; = −q e = −q
dx dx dx 2



Vigas Não Prismáticas : seção variável com x.

d 2v M d 2v
= → EI ( x ) ⋅ 2 = M
dx 2 EI ( x ) dx

dM d d 2v 
=V →  EI(x) ⋅ 2  = V
dx dx 
 dx  
dV d2  d 2v 
= −q →  EI ( x) ⋅ 2  = −q
dx dx 2 
 dx  


Vigas Prismáticas: rigidez (EI) constante
Momento Fletor:
d 2v M d 2v
= → EI z ⋅ 2 = M → EI z ⋅ v ′′ = M
dx 2 EI z dx
Força de Cisalhamento:
dM d 3v
=V → EI z ⋅ =V → EI z ⋅ v ′′′ = V
dx dx 3
Carregamento:
dV d 4v
= − q → EI z ⋅ = −q → EI z ⋅ v ''' ' = − q
dx dx 4



Condição de Contorno: relativas às deflexões e
rotações nos apoios.

→ v=0 e M =0

→ v=0 e M =0

→ v = 0 e v′ = 0


rotações em vigas biapoiadas.

x = 0 → v = 0 e v′′ = 0 pois M = 0

x = L → v = 0 e v′′ = 0 pois M = 0



rotações em vigas engastadas.

 x = 0 → v = 0 e v′ = 0

 x = L → v ′′ = 0 pois M = 0
 x = L → v ′′′ = 0 pois V = 0



Condição de Continuidade:

No ponto C:
(v )AC = (v )CB
(v ′ )AC = (v ′ )CB



Exemplo1: Determine a equação da Linha
Elástica para a viga abaixo. Determine também a
deflexão máxima δmáx e os ângulos de rotação θA
e θB nos apoios.


a) Expressão para o Momento Fletor:

q⋅L
Reações de apoio: RVA = RVB =
2
Momento Fletor:
qL x qL q
M = ⋅x− q⋅x⋅ = ⋅ x − ⋅ x2
2 2 2 2



b) Equação da Linha Elástica:
qL q
EI z ⋅ v '' = M = ⋅ x − ⋅ x 2 [.(dx)]
2 2
qL q
EI z ⋅ v '' ⋅ dx = ⋅ x ⋅ dx − ⋅ x 2 ⋅ dx
2 2
qL q 2
EI z ∫ v '' ⋅ dx = ∫ x ⋅ dx − 2 ∫ x ⋅ dx 1ª integração
2
(EI z ⋅ v ' ) = ∫  qL ⋅ x2 − q ⋅ x3 + C1 
2 3

∫ 
 2
 2



2ª integração

qL x 3 q x 4
EI z ⋅ v = ⋅ − ⋅ + C1 ⋅ x + C 2
4 3 6 4


Condições de Contorno:
(I) x = 0 → v = 0
L
(II) x = L → v = 0 e x = → v′ = 0
2

(I) x = 0 → v = 0∴ 0 = 0 − 0 + 0 + C2 → C2 = 0

qL q
(II) x = L → v = 0∴ 0 = .L3 − .L4 + C 1 .L + 0
12 24
qL 4 qL 4
qL 4
qL 3
0 = − + C 1 .L = + C 1 .L → C 1 = −
12 24 24 24



qL q
EI z ⋅ v = ⋅ x3 − ⋅ x 4 + C1 ⋅ x + C 2 → deflexão
12 24

1  qL q qL 3 
v = 
 12 ⋅x −
3
⋅x +
4
⋅x

EI z  24 24 
q  L 1 L3 
v= 
 12 ⋅x −
3
⋅x +
4
⋅x Linha Elástica
EI z  24 24  


qL 2 q 3
EI z ⋅ v′ = ⋅ x − ⋅ x + C1 → rotação
4 6
1  qL 2 q 3 qL3 
v′ =  4 ⋅ x − 6 ⋅ x − 24 
 
EI z  

q  L 2 1 3 L3 
v′ =  ⋅x − ⋅x −
4  → rotação θ
EI z  6 24 




c) Deflexão máxima x = L/2:

q  L  L 3 1  L 4 L3 L 
vmáx =  ⋅  − ⋅  − ⋅ 
EI z 12  2  24  2  24 2 
 
q  L4 L4 L4 
vmáx =  − − 
EI z  96 384 48 
5qL4
vmáx = −
384 ⋅ EI z


d) Ângulos de rotação: θA e θB

qL 3
θ A → x = 0∴ v ′A = −
24 EI z

qL 3
θB → x = L∴ v′ =
B
24 EI z



Exemplo 2: Calcular a deflexão e a inclinação
(rotação) do ponto D indicado na viga
representada abaixo, adotando E = 10GPa.
1,2kN/m

16cm
A B
D
6cm
2,2m 3m

a) Reações de apoio:
qL 1,2 × 5,20
RVA = RVB = = = 3,12 KN
2 2


b) Equação diferencial da linha elástica:

EI z ⋅ v '''' = − q = − 1, 2
EI z ⋅ v ′′′ = − 1, 2 ⋅ x + C1
x2
EI z ⋅ v ′′ = − 1, 2 ⋅ + C1 ⋅ x + C 2
2
x3 x2
EI z ⋅ v ′ = − 1, 2 ⋅ + C1 ⋅ + C 2 ⋅ x + C3
6 2
x4 x3 x2
EI z ⋅ v = − 1, 2 ⋅ + C1 ⋅ + C2 ⋅ + C3 ⋅ x + C4
24 6 2



c) Condições de Contorno:

(I) x = 0 → V A = 3,12 KN = v′′′ ⇒ C1 = 3,12

(II) x = 0 → M A = 0 = v′′ ⇒ C 2 = 0

L
(III) x = = 2,60 → v′ = 0
2
2 .6 3 2,6 2
0 = −1,2 ⋅ + 3,12 ⋅ + 0 ⋅ x + C 3 ⇒ C 3 = −7 ,03
6 2
(IV) x = 0 → vA = 0 ⇒ C4 = 0


d) Rotações e deflexões:
kN
E = 10 GPa = 10 × 10 6 2
m
bh 3
0 , 06 × 0 ,16 3
Iz = = = 2 , 048 . 10 − 5 m 4
12 12
EI z = 204 ,8 kN ⋅ m 2

v′ =
1
EI z
(
⋅ − 0 , 2 ⋅ x 3 + 1,56 ⋅ x 2 − 7 , 03 )
v=
1
EI z
(
. − 0 , 05 ⋅ x 4 + 0 ,52 ⋅ x 3 − 7 , 03 ⋅ x )



e) Deflexão e Rotação no Ponto D:

Para x = 2,20m

v′ =
1
204,8
( )
⋅ − 0,2 × 2,23 + 1,56 × 2,2 2 − 7,03 = −7,9 ×10−3 rad

v=
1
204,8
( )
⋅ − 0,05 × 2,2 4 + 0,52 × 2,23 − 7,03 × 2,2 = −5,65 ×10−2 m


Exemplo 3: Determine a equação da Linha
Elástica para uma viga engastada mostrada
abaixo. Determine também θB e δB na
extremidade livre.



Reações de apoios:
qL2
RVA = qL MA =
2
a) Momento Fletor na viga:
qL2 x
M =− + qLx − qx
2 2
qL2 x2
M =− + qLx − q
2 2


qL2 qx 2
EI z ⋅ v = M = −
''
+ qLx −
2 2
q  L 2
x 
2

∫ v′′ = ∫ EI z ⋅  − 2 + Lx − 2 




q  L x 2 x3 
∫ v = ∫ EI z
⋅  − ⋅ x + L ⋅ − + C1  → Rotação
'
 
 2 2 6 
q  L2 x 2 Lx 3 x 4 
v= ⋅− + − + C1 ⋅ x + C 2  → Deflexão
EI z 
 4 6 24 




Condição de Contorno:
(I) x = 0 → v' = 0

(II) x = 0 → v = 0

⋅ (− 0 + 0 − 0 + C1 ) ⇒ C1 = 0
q
(I) 0=
EIz

⋅ (− 0 + 0 − 0 + C2 ) ⇒ C2 = 0
q
(II) 0 =
EIz


Rotação:
q  L2 L 2 x3 
v =
'
⋅− ⋅ x + ⋅ x − 
 2
EI z  2 6 

v' =
qx
6 EI z
(
⋅ − 3L2 + 3 Lx − x 2 )

qL3
θB = v′ → x = L ∴
B v′ = −
B
6EIz



Deflexão:
q  L2 2 L 3 1 4 
v= ⋅− ⋅ x + ⋅ x − ⋅ x 
EI z  4
 6 24 


v=
qx 2
24 EI z
(
⋅ − 6 L2 + 4 Lx − x 2 )

qL4
δ B = vB → x = L ∴ vB = −
8EIz


Exemplo 4: Determine a equação da Linha
Elástica, os ângulos de rotação θA e θB nos
apoios, a deflexão máxima δmáx e a deflexão δC
no ponto médio.



Reações de apoio:
P⋅b P⋅ a
RVA = e RVB =
L L
a) Momentos Fletores:

Pb
M= ⋅ x (0 ≤ x ≤ a)
L
M = ⋅ x − P ⋅ (x − a) (a ≤ x ≤ L)
Pb
L


Pb
EI ⋅ v ′′ = ⋅x (0 ≤ x ≤ a)
L
⋅ x − P ⋅ (x − a )
Pb
EI ⋅ v ′′ = (a ≤ x ≤ L)
L



Integrando temos: Rotações
Pb 2
EI ⋅ v ′ = ⋅ x + C1
2L
Pb 2 P ⋅ ( x − a ) 2
EI ⋅ v ′ = ⋅x − + C2
2L 2
Integrando novamente: Deflexões
Pb 3
EI ⋅ v = ⋅ x + C1 ⋅ x + C 3
6L
Pb 3 P ⋅ ( x − a ) 3
EI ⋅ v = ⋅x − + C2 ⋅ x + C4
6L 6


(I) x = 0 → v = 0

(II) x = L → v = 0

(III) x = a → vesq = v′
′ dir

(IV) x = a → vesq = vdir




(I) x = 0→ v = 0 ⇒ C3 = 0

PbL3 P ⋅ ( L − a)3
(II) x = L → v = 0∴ 0 = − + C2 ⋅ L + C4
6L 6
Pba2 Pba2 P(a − a)2
(III) x = a → +C1= − + C2 ⇒ C1 = C2
2L 2L 2


Pba 3 Pba 3 P ( a − a ) 3
(IV) x = a → +C 1⋅a = − + C2 ⋅ a + C4
6L 6L 6
C1 ⋅ a = C 2 ⋅ a + C 4 ⇒ C1 ⋅ a = C1 ⋅ a + C 4 ⇒ C 4 = 0
PbL 2 Pb 3
(II) − + C 2 ⋅L + C 4 = 0
6 6
Pb
6
( )
⋅ L2 − b 2 = − C 2 ⋅ L

C2 = −
Pb
6L
( )
⋅ L2 − b 2 = C1



Deflexões:
v=
1
EI
 Pbx 3 Pb 2
⋅ − (
⋅ L − b2 )x 

 6L 6L 
v=
Pbx
6 LEI
(
⋅ x 2 − L2 + b 2 ) (0 ≤ x ≤ a)

1  Pbx 3 P ⋅ (x − a ) 
( )
2
Pb
v = ⋅ − − ⋅ L2 − b 2 ⋅ x 
EI  6 L 6 6L 
P ⋅ ( x − a)
( )
3
Pbx
v=− ⋅ L2 − b 2 − x 2 − (a ≤ x ≤ L)
6 LEI 6 EI


Rotações:
⋅ (L − b 2 )
1  Pbx 2 Pb 2 
v ′= ⋅ −
EI  2 L 6L 
v′ = −
Pb
6 LEI
(
⋅ L2 − b 2 − 3 x 2 ) (0 ≤ x ≤ a)

1  Pbx 2 P ⋅ (x − a )
( )
2
Pb
v′ = ⋅ − − ⋅ L2 − b 2 
EI  2 L 2 6L 
P ⋅ (x − a )
⋅ (L − b − 3 x ) −
2
Pb
v =−
' 2 2 2
(a ≤ x ≤ L)
6 LEI 2 EI



Cálculo de θA:
θ A = v ′A → x = 0 ( L + b) ⋅ ( L − b)

v′ = −
A
Pb
6 LEI
(
⋅ L2 − b 2 )
Pab (L + b )
v′ = −
A
6 LEI


Cálculo de θB:
θ B = v′ → x = L
B
(b)
P (L − a )
( )
2
Pb
v′ = −
B ⋅ L − b − 3L −
2 2 2

6 LEI 2 EI
Pb  (− 2 L − b )
2 2

v′ = −
B ⋅ + b
2 EI  3L 
Pb  2 L + b − 3 Lb 
2 2
v′ =
B ⋅ 

2 EI 3L 
Pab ⋅ ( L + a )
v′ =
B
6 LEI



Deflexão máxima δmáx:
Ponto de máximo v′ = 0

−
Pb
6 LEI
( )
⋅ L2 − b 2 − 3 x 2 = 0

L2 − b 2
x1 =
δ máx = vmáx para ( x = x1 ) 3
 2

Pb L2 − b 2  L2 − b 2 
vmáx = ⋅ ⋅   − L2 + b 2 
6 LEI 3  3  
  
( )
3
Pb ⋅ L2 − b 2 2

vmáx =− (a ≥ b)
9 3 ⋅ LEI


Deflexão no ponto médio x = L/2:
L
δ C = v C para x =
2
L
Pb ⋅
2 ⋅  L  − L2 + b 2 
2

vC =   
6 LEI  2 
 

Pb  L2 
vC = ⋅ − L2 + b 2 
12 EI  4 


vC =
Pb
48 EI
(
⋅ − 3 L2 + 4b 2
) (a ≥ b)


4.2 Vigas Estaticamente Indeterminadas

São vigas em que o número de reações excede o
número de equações de equilíbrio da estática.

∑ Fx = 0 ⇒ H A = 0 3 reações
∑ FY = 0 ⇒ R A + R B − qL = 0 2 equações
Estaticamente Indeterminadas
L
∑ M A = 0⇒ M A − qL .
2
+ R B .L = 0


São necessárias equações adicionais para obter todas
as reações.
O número de reações em excesso ao número de
equações de equilíbrio é chamado de Grau de
Hiperestaticidade.

Grau = (nº Reações) – (nº Equações)

Assim, a viga analisada é hiperestática de grau 1.



As equações adicionais podem ser obtidas
considerando as deformações da estrutura.
Logo, pode-se usar uma das três equações diferenciais
da linha elástica:

EI z ⋅ v′′ = M
EI z ⋅ v′′′ = Q
EI z ⋅ v '''' = −q

O procedimento para resolução é o mesmo usado para
vigas isostáticas.


Como exemplo, analisaremos a viga anterior
determinando as rotações e deflexões da viga.



a) Estaticidade da estrutura:
HA = 0
M A , RVA , RVb → 3 reações desconheci
das,

∑F Y =0 e ∑M = 0 → 2 equações de equilíbrio

Grau = 3 – 2 = 1 Estrutura estaticamente indeterminada de grau 1

b) Equações de equilíbrio:
(1) RVA + RVB = qL
qL2
(2) M A + RVB ⋅ L =
2


c) Equação no momento fletor:
Reação redundante reação em excesso que pode ser
liberada da estrutura, porém, deixando-a estável e
estaticamente determinada.
Escolhemos RVB como reação redundante, e as outras
reações serão escritas em função desta.

RVA = qL − RVB
qL2
MA = − RVB ⋅ L
2
qx 2  qL2  qx 2
M = RVA ⋅ x − M A − = (qL − RVB ) ⋅ x − 
 − RVB .L  −
 2
2  2 



d) Equação diferencial da Linha Elástica:
 qL2  qx 2
EI z ⋅ v ′′ = M = (qL − RVB ) ⋅ x − 
 2 − RVB ⋅ L  − 2

 
Integrando:
x 2  qL2  qx 3
EI z ⋅ v ′ = (qL − RVB ) ⋅ −  − RVB ⋅ L 
⋅x − + C1
2  2   6
x 3  qL2  x 2 qx 4
EI z ⋅ v = (qL − RVB ) ⋅ −  − RVB ⋅ L  ⋅ −
 2 24 + C1 ⋅ x + C2
6  2
 
3 incógnitas C1, C2 e RVB
São necessárias 3 condições de contorno


e) Condições de contorno:
(I) x = 0 → v' = 0
(II) x=0→v=0
(III) x=L→v=0

(I ) → 0 = 0 − 0 − 0 + C1 ⇒ C1 = 0

( II ) → 0 = 0 − 0 − 0 + 0 + C 2 ⇒ C 2 = 0



L 3  qL 2  L2 qL 4
(III) → 0 = (qL − R VB ) ⋅ −
 2 − R VB ⋅ L ⋅
 2 −
6   24

qL 4 R VB L3 qL 4 R VB L3 qL 4
0= − − + −
6 6 4 2 24
1 1 1 1 1  RVB qL
RVB L3 ⋅  −  = qL4 ⋅  − −  ∴ - =−
6 2  6 4 24  3 8
3qL
RVB =
8


f) Rotações e Deflexões:
1  3qL  x 2  qL2 3qL  qx3 
v' = ⋅  qL −  ⋅ − − ⋅ L ⋅ x − 

EI z 8  2  2 8 
 6 

v' =
qx
48 EI z
(
⋅ − 6 L 2 + 15 L ⋅ x − 8 ⋅ x 2 )
1  3qL  x3  qL2 3qL  x 2 qx4 
v= ⋅  qL − ⋅ − − ⋅ L⋅ −
 2 24 
EI z  8  6  2
 8  

v = −
qx 2
48 EI
(
⋅ 3 L2 − 5 L ⋅ x + 2 ⋅ x 2 )
z



g) Reações nos apoios:

3qL 5qL
RVA = qL − RVB = qL − =
8 8
qL2 qL2 3qL qL2
MA = − RVB ⋅ L = − ⋅L =
2 2 8 8

4.3 Método da Superposição

Em uma viga submetida a várias cargas, os
deslocamentos em um ponto qualquer pode ser obtido
somando-se algebricamente os deslocamentos, no
mesmo ponto, correspondente à cada carga agindo
isoladamente.
Exemplo 1:
P



P

qL4
(v B )q =− (v B )P =−
PL3
8 EI z 3 EI z
PL2
(θ B )q =−
qL3
(θ B )P =−
6 EI z 2 EI z


qL 3 PL 3
v B = (v B )q + (v B )P =− −
8 EI z 3 EI z

qL3 PL 2
θ B = (θ B )q + (θ B )P =− −
6 EI z 2 EI z



Exemplo 2:


δ c = (vC )q + (vC )P
θ A = (v′A ) q + (v′A ) P 

 −θA = θB
θ B = (v ′ ) q + (v ′ ) P 
B B 

5qL4
(vC )q =− (vC )P =−
PL3
384 EI z 48EI z

qL3
− (v′ )q = (v′ )q
A B = − (v ′ )P = (v ′ )P =
A B
PL 2
24 EI z 16 EI z



5 qL4 PL3
δC = − −
384 EI z 48 EI z

qL3 PL2
−θ A = θB = +
24EIz 16EIz


Exemplo 3: Determine δB e θA



2
∑M A = aF − ⋅ aP = 0
3
2
F = ⋅P
3


Viga Engastada:

qb4
(vB )q =
8EI
Fb3
(vB )F =
3EI

 qb4 Fb3   qb4 2Pb3 
δ B = −
 +  = − + 
 8EI 3EI   8EI 9EI 
  



P Viga Apoiada:
δB
θ1
qb 4 2 Pb 3
θ1 =
θ2 δB
= +
a 8 aEI 9 aEI
a
 2a   a   a
P ⋅  ⋅  ⋅ a + 
Pab ⋅ (L + b )  3  3  3 4 Pa 2
θ2 = = =
6 L ⋅ EI 6 a ⋅ EI 81 ⋅ EI

qb 4 2 Pb 3 4 Pa 2
θ A = −θ 1 − θ 2 = − − −
8 aEI 9 aEI 81 EI


Exemplo 4: Determinar θA ; δB ; θC ; θD e δD
30 kN
20 kN/m

10 kN/m 20 kN

A
B C D
3m 3m 2m

Sistema Equivalente:
30 kN
20 kN/m
20 kN
10 kN/m 40 kN

A C 60kNm C D
B
3m 3m 2m



Rotação em A:
qL 3 3 qL 3 PL 2 ML
θA = − − − +
24 EI 128 EI 16 EI EI
10 × 63 3 ×10 × 63 30 × 6 2 60 × 6 148,125
θA = − − − + =−
24 EI 128EI 16 EI 6 EI EI
Flecha em B:
5 qL 4 5 qL 4 PL 3 ML 2
δB = − − − +
384 EI 768 EI 48 EI 16 EI

5 ×10 × 64 5 ×10 × 6 4 30 × 63 60 × 62 253,125
δB = − − − + =−
384EI 768EI 48EI 16EI EI


Rotação em C:
qL3 7 qL3 PL 2 ML
θC = + + + −
24 EI 384 EI 16 EI 3 EI

10 × 63 7 ×10.63 30 × 62 60 × 6 76,875
θC = + + + − =
24EI 384EI 16EI 3EI EI



Flecha em D:

θC δ’D 76,875 153,750
δ D' = θC × L = ×2 =
EI EI
δ’’D
10 × 2 4 20 × 2 3 73,333
δD
θ’D
=− − =−
''

8 EI 3 EI EI

73,333 153,750 80,417
δ D = δ D '' + δ D ' = − + =
EI EI EI


Rotação em D :

θC δ’D

10 × 23 20 × 22 53,333
δ’’D θD = − '
− =−
θ’D 6EI 2EI EI
53,333 76,875 23,542
θ D = θ D ' + θC = − + =
EI EI EI


4.4 Método da Superposição Aplicado em
Vigas Estaticamente Indeterminadas
Exemplo 5: Determine as reações dos apoios da
viga abaixo usando o Método da Superposição.

a) Estaticidade:
Grau = 4(eq.) – 3(reações) = 1 Hiperestática
Reação Redundante RVB

b) Equação de Equilíbrio:

∑F Y = 0 ∴ RVA + RVB − qL = 0 ⇒ RVA = qL − RVB

qL2 qL2
∑ M A = 0 ∴ M A + RVB ⋅ L − 2 = 0 ⇒ M A = 2 − RVB ⋅ L


c) Compatibilidade de deslocamento:

(δ B )q + (δ B )R
VB
=0

qL 4 R VB ⋅ L 3 3 qL
− + = 0 ⇒ R VB =
8 EI 3 EI 8

d) Reações dos apoios:

3qL 5 qL
RVA = qL − RVB = qL − =
8 8
3qL
RVB =
8
qL2 qL2 3qL qL2
MA = − RVB ⋅ L = − ⋅L =
2 2 8 8


Exemplo 6: Determinar:
a) a reação em cada apoio;
b) a declividade da linha elástica na extremidade A.

q

A C
B
2L/3 L/3
L

a) Estaticidade:
4-3=1 Hiperestática RVB Reação Redundante

b) Equações de Equilíbrio:

∑F X = 0 ⇒ R HC = 0

∑F Y = 0 ⇒ RVA + RVB + RVC = qL∴RVA + RVC = qL− RVB
2L qL2 qL 2R
∑ M A = 0 ⇒ RVB. 3 + RVC .L = 2 ∴ RVC = 2 − 3VB


c) Compatibilidade de deslocamento:

q

A C A C
B
RVB
2L/3 L/3 2L/3 L/3

(v )q = −
qx
24 EI
(
⋅ L3 − 2 Lx 2 + x 3 )
onde x =
2L
3
q 2L  3  2 L   2L  
2 3
qL4
(δ B )q =− ⋅ ⋅  L − 2L  +    = −0,01132
24EI 3    3   3    EI

(v )R VB
= −
Pbx
6 LEI
(
⋅ L2 − b 2 − x 2 ) onde x=
2L
3

(− RVB ) ⋅  L 
 
 3  ⋅ 2 L ⋅  L2 −  L  −  2 L   = RVB ⋅ L ⋅ 4 L
2 2 2
(δ B )R =−      
VB
6 LEI 3    3   3   27 EI 9

R VB ⋅ L3
(δ B )V = 0 , 01646 ⋅
B
EI


Sabendo-se que δB = 0 e

δB = (δB )q + (δB )RVB

qL 4
RVB ⋅ L3
0 = −0,01132 ⋅ + 0,01646 ⋅ ⇒ RVB = 0,688 ⋅ qL
EI EI
Logo:
qL 2 RVB qL 2
RVC = − = − ⋅ 0,688 qL = 0,0413 ⋅ qL
2 3 2 3
RVA + RVC = qL − RVB
RVA = qL − 0 ,688 ⋅ qL − 0 ,0413 ⋅ qL = 0 , 271 ⋅ qL

d) Declividade no apoio A:
θA = (θA )q + (θA )R
VB

qL3
(θ A )q = −
24EI
 2L   L   L
RVB ⋅   ⋅   ⋅  L + 
Pab⋅ (L + b)  3   3  3
(θ A )R = =
VB
6LEI 6LEI

 8L3 
0,688 ⋅ qL ⋅ 
 27  0,03398⋅ qL3

(θ A )R =  =
VB
6LEI EI


d) Declividade no apoio A:

qL3 0,03398 ⋅ qL3 qL3
θA = − + = −0,00769 ⋅
24 EI EI EI

Aplicações
Aplicação 1: Sabendo que a viga AE é um perfil
laminado de aço S310x47,3, que q = 50kN/m, a = 1,5m
e E = 200GPa, determinar: (a) a declividade em B; (b) a
deflexão no centro C da viga.
Perfil S310x47,3 A = 6032mm2; Ix = 90,7x106mm4;
Iy = 3,9x106mm4

q

A B C D E
a 2a a


Aplicações
Aplicação 2: Para a viga em balanço com
carregamento mostrado, determine a declividade e a
deflexão nos pontos B e D.
q

A D
B C
a a a

Aplicações
Aplicação 3: A viga em balanço tem seção circular
com diâmetro de 45mm e está submetida ao
carregamento mostrado. Determine a inclinação e a
deflexão nos pontos B e C. Considera E = 200GPa.

0,6kN
2,6kN/m

B
A C

0,75m 0,25m


Aplicações
Aplicação 4: Para o carregamento mostrado na figura,
sabendo-se que as vigas AC e BD têm mesma rigidez à
flexão, determine a reação em B.

10kN/m

Capitulo4 deflexaode vigas

Recomendados

Recomendados

Más contenido relacionado

La actualidad más candente

La actualidad más candente (20)

Destacado

Destacado (20)

Similar a Capitulo4 deflexaode vigas

Similar a Capitulo4 deflexaode vigas (20)

Capitulo4 deflexaode vigas