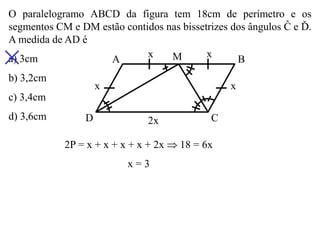
O paralelogramo ABCD da figura tem 18cm de perímetro e os segmentos CM e DM estão contidos nas bissetrizes dos ângulos Ĉ e Ď. A medida de AD é
a) 3cm
b) 3,2cm
c) 3,4cm
d) 3,6cm
A
M
B
C
D
x
x
x
x
2x
2P = x + x + x + x + 2x  18 = 6x
x = 3

Num trapézio isósceles, as bases medem 8cm e 3cm e os ângulos da base medem 60º. Seu perímetro é
a) 20cm
b) 21cm
c) 22cm
d) 24cm
3
60º
60º
2,5
8
2,5
3
x
x
cos 60º =
2,5
x
2,5
x
1
2
=
x = 5
2P = x + x + 8 + 3
2P = 10 + 11
2P = 21

Eqüilátero
Num losango, um dos ângulos internos é o dobro do outro. Se a menor de suas diagonais mede x, seu perímetro é
a) 3x
b) 2 3 x
c) 3 2 x
d) 4x
x
a
a
a
a
a
a
x
x
x
x
2P = x + x + x + x = 4x

Na figura, ABCD é um retângulo. E e F são os pontos médios dos lados AD e CD, respectivamente. Podemos concluir que:
a) EF = AD
b) EF = AB
2
c) EF = BD
2
d) EF = FC
D
A
E
B
C
F

As bases de um trapézio medem 4cm e 12cm. As diagonais desse trapézio dividem sua base média em três segmentos adjacentes proporcionais a
a) 1, 2 e 1.
b) 2, 3 e 2.
c) 1, 2 e 3.
d) 1, 3 e 1.
4
12
2
2
8
4

As diagonais de um quadrilátero convexo medem 8m e 12m. Os pontos médios dos lados desse quadrilátero são vértices de um outro quadrilátero. Ele é um
a) paralelogramo de 20m de perímetro.
b) paralelogramo de 24m de perímetro.
c) quadrilátero, não necessariamente paralelogramo, de 20m de perímetro.
d) quadrilátero, não necessariamente paralelogramo, de 24m de perímetro.
8
12
6
6
4
4

Em um triângulo, o ponto de encontro das bissetrizes internas, o ponto de encontro das alturas, o ponto de encontro das medianas e o ponto de encontro das mediatrizes dos lados denominam-se, respectivamente,
a) circuncentro, ortocentro, baricentro e incentro.
b) incentro, ortocentro, baricentro e circuncentro.
c) incentro, baricentro, ortocentro e circuncentro.
d) circuncentro, baricentro, ortocentro e incentro.

Num triângulo ABC, AB = 6cm e AC = 8cm. Pelo incentro I do triângulo, traça-se uma paralela a BC, que corta AB em M e AC em N. Calcule o perímetro do triângulo AMN.
B
A
C
b
b
c
c
a
a
2b
2c
2a
6
8
b
x
x
c
y
y
M
N
6 – x
8 – y
2P = x + y + (8 – y) + (6 – x)
2P = 8 + 6 = 14

Na figura, M e N são os pontos médios dos lados AB e AC do triângulo ABC. Assinale a afirmativa FALSA.
a) MN // BC
b) MN = BC
2
c) BP = 2.PN
d) MC = AC + BC
2
M
N
P
B
C
A

A36. Os raios de dois círculos medem 6cm e 8cm. Determine a distância d entre seus centros em cada caso.
a) Eles são tangentes internamente.
b) Eles são tangentes externamente.
c) Um deles é interior ao outro.
d) Um deles é exterior ao outro.
e) Elas são secantes.
a) d = R – r  d = 8 – 6 = 2cm
b) d = R + r  d = 8 + 6 = 14cm
c) 0  d < R – r  0  d < 2
d) d > R + r  d > 14
e) R – r < d < R + r  2 < d < 14

A37. Dois círculos de raios 3cm e 4cm são tangentes externamente. Cada um deles tangencia, internamente, um terceiro círculo de raio 12cm. Calcule o perímetro do triângulo cujos vértices são os centros dos três círculos.
3 + 4
12 – 3
12 – 4
2P = 12 – 4 + 3 + 4 + 12 – 3 = 24

Na figura, AC é um diâmetro do círculo e as retas r e s são tangentes ao círculo em A e B. Podemos afirmar que:
a)  = 2
b)  +  = 90º
c)  = 3
d)  + 2 = 90º


C
s
B
A
P
r
90 – 
90 – 
–2 + 180º +  = 180º
 = 2

Os segmentos PA, PB e QR são tangentes ao círculo da figura em A, B e C, respectivamente. Se PA = 8, calcule o perímetro do triângulo PQR.
B
A
P
C
Q
R
2P = 8 – y + y + 8 – x + x = 16
x
y
8 – x
x
y
8 – y

Um triângulo ABC está circunscrito a um círculo. Os lados AB = 5cm, AC = 8cm e BC = 9cm tangenciam um círculo em M, N e P, respectivamente. Calcule AM.
A
B
C
M
N
P
x
x
y
y
z
z
x + y = 5
x + z = 8
y + z = 9
x + y = 5
x + z = 8
–y – z = –9
2x = 4
x = 2

Tornam-se, ordenadamente, sobre um círculo de centro O, dez pontos A1, A2, A3 ..., A10. Eles dividem o círculo em dez arcos congruentes. Calcule os ângulos internos:
a) do triângulo A10A3;
b) do quadrilátero A1A3A5A8.
O
A6
A1
A2
A3
A4
A5
A7
A8
A9
A10
36º
36º
A6
A1
A2
A3
A4
A5
A7
A8
A9
A10
72º
x
x
2x + 72º = 180º  x = 54º
a)
b)
36º
36º
36º
36º
36º
36º
36º
36º
36º
36º
90º
90º
72º
108º

(Cesgranrio) Em um círculo de centro O, está inscrito o ângulo . Se o arco AMB mede 130º, o ângulo  mede
a) 25º
b) 30º
c) 40º
d) 45º
O

A
B
M
130º
180º
2
2 + 180º + 130º = 360º
 = 25º

Na figura, O é o centro do círculo. Se a, b e c são as medidas dos ângulos assinalados, então
a) b = a + c
b) a = b + c
c) a + b = 90º + c
d) a + c = 90º – b
O
A
B
a
b
c
c + 2a = a + b
c + a = b  b = a + c
2a
2a
a + b

(UFES) Na figura, a medida de , em graus, é
a) 52
b) 54
c) 56
d) 58

32º
58º
2
2 = 58º  2
 = 58º

(Mack-SP) Na figura, sabe-se que m(CÂD) = 20º e m(CÊD) = 70º. Então, a medida de AMB é igual a
a) 50º
b) 45º
c) 60º
d) 30º
O
B
A
E
D
C
M
x
20º
100º
40º
70º
110º
50º
x =
100º – 40º
2
x = 30º

(VUNESP) Sejam A, B e C pontos distintos no interior de um círculo, sendo C o centro do mesmo. Se construirmos um triângulo, inscrito no círculo, com um lado passando por A, outro por B e outro por C, podemos afirmar que este triângulo
a) é acutângulo
b) é retângulo
c) é obtusângulo
d) pode ser eqüilátero
C
A
B
diâmetro
180º
90º

Na figura, ABC é um triângulo inscrito no círculo, sendo BC diâmetro. A reta t é tangente ao círculo em A;  e  são os ângulos que t forma com AB e AC, respectivamente, e  –  = 38º. O ângulo Ĉ do triângulo ABC mede
a) 58º
b) 60º
c) 62º
d) 64º
A
t
B
C


90º
 –  = 38º
 +  = 90º
2 = 128º
 = 64º
128º
64º

As retas r e s da figura tangenciam o círculo em A e B. Então a medida x do ângulo assinalado é:
a) 60º
b) 65º
c) 70º
d) 75º
P
A
B
s
r
x
50º
2x
65º
65º
2x = 130º
x = 65º

Na figura, PBA e PDC são secantes ao círculo. AB é lado de um quadrado e CD é lado de um Hexágono regular inscritos no círculo. Se o arco AC é o dobro do arco BD, então as medidas do ângulo P e AMC são, respectivamente:
a) 30º e 110º
b) 35º e 105º
c) 36º e 104º
d) 40º e 100º
P
A
M
C
D
B
x
60º
90º
2x
b
a
3x + 90º + 60º = 360º
3x = 210º
x = 70º
a =
140º – 70º
2
= 35º
b =
140º + 70º
2
= 105º

30º
Na figura, AB = 8 é diâmetro do círculo e P é o ponto médio de AQ. O perímetro do triângulo ABQ é
a) 22
b) 23
c) 24
d) 25
A
P
B
Q
60º
8
4
4
sen 30º =
x
8
1
2
 8 = x
x
x = 4
2P = 8  3 = 24
O triângulo é eqüilátero

As bases de um trapézio isósceles circunscrito a um círculo medem 5 e 9. Calcule a medida de cada um dos lados não-paralelos.
x
x
x
x
y
y
y
y
9
5
2x = 5  x = 2,5
2y = 9  y = 4,5
x + y = 2,5 + 4,5 = 7

A52. Dois lados consecutivos de um quadrilátero circunscrito a um círculo medem 6cm e 8cm. Calcule as medidas dos outros dois lados do quadrilátero, sabendo que seu perímetro é 30cm.
a
a
b
b
6
6 – a
6 – a
8
2 + a
2 + a
a + b + 2 + a + b + 8 + 6 = 30
2a + 2b = 14
a + b = 7
l1 = a + b = 7
l2 = a + 2 + b = 7 + 2 = 9

A53. Um quadrilátero convexo está inscrito a um círculo. Dois de seus ângulos internos medem 85º e 113º. A diferença das medidas dos outros dois ângulos internos é
a) 23º
b) 25º
c) 28º
d) 32º
85º
113º
Dois ângulos opostos de um quadrilátero inscrito são sempre suplementares
85º + x = 180º
x = 95º
95º
113º + y = 180º
y = 67º
67º
95º – 67º = 28º

Um trapézio está inscrito em um círculo. Então, podemos afirmar que
a) ele pode ser um trapézio retângulo.
b) a soma das medidas de suas bases é igual à soma das medidas dos lados não-paralelos.
c) pelo menos uma de suas diagonais pode passar pelo centro do círculo.
d) conhecendo-se a medida de um dos seus ângulos internos, é possível determinar as medidas dos outros três ângulos internos.
a
a
b
b
a e b são suplementares

As afirmativas abaixo se referem à possibilidade de polígonos serem inscritos ou circunscritos em um círculo. Assinale a alternativa FALSA.
a) Todo triângulo é inscritível e circunscritível.
b) Todo retângulo é inscritível mas pode não ser circunscritível.
c) Todo losango é inscritível e circunscritível.
d) Todo quadrado é inscritível e circunscritível.
Um quadrilátero só é inscritível se os ângulos opostos forem suplementares, o que não ocorre em alguns losangos.
Não é inscritível

Num quadrilátero ABCD, inscrito em um círculo, os pontos A e C são diametralmente opostos e Ĉ = 2Â. Calcule, em radianos, as medidas dos ângulos internos desse quadrilátero.
A
B
C
D
a
2a

2

2
a + 2a = 
a =

3
2a =
2
3
2
3

3
;

2
;
;

2