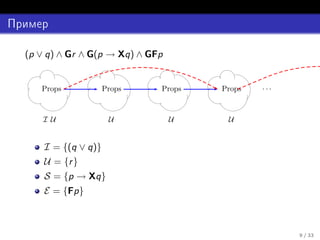
El documento describe la lógica temporal LTL (Lógica Temporal Lineal) y cómo convertir fórmulas LTL a forma normal disyuntiva simplificada (DSNF). Explica los operadores LTL como F, G, U, W y cómo negarlos. Luego detalla el proceso de conversión de una fórmula LTL a una fórmula equivalente en DSNF mediante la introducción de proposiciones auxiliares.

1. þ
½¼
ÄÌÄ
º
ý
ÓÒ ÚÐ Ú ÖÔÓÓк
ºÙ
Ä Ú ÖÔÓÓÐ ÍÒ Ú Ö× ØÝ
¹ ¾¼¼
½ » ¿¿

2. ÄÌÄ
Prop
ØÖÙ ¸ Ð× ¸ ¬¸ ∨¸ ∧¸ → ≡º
þ ¸X¸ F¸ G¸ U Wº
´WFF µ
ØÖÙ Ð×
ϕ ψ ¸ 
¬ϕ¸ ϕ ∧ ψ ¸ ϕ ∨ ψ ¸ ϕ → ψ ¸ ϕ ≡ ψ 
 
Xϕ





Fϕ

Gϕ 



ϕUψ





ϕWψ
¾ » ¿¿

3. ÄÌÄ
¸
Nº
ÄÌĸ σ¸
σ = s0 , s1 , s2 , s3 , . . .
si
¸ i¹
º
i ∈ Nº
(σ, i ) |= A
p ¸q p ¸¬q p ¸¬q ¬p ¸q p ¸q
¿ » ¿¿

4. ÄÌÄ
S ÄÌÄ
ϕ ¸ S ϕ¸ º º¸
S |= ϕ.
ψS º º S |= ϕ º º¸
ψS → ϕ º
ÄÌÄ
ÈËÈ
¸ ¸
O(|S| · 2|ϕ| ).
» ¿¿

5. ü
ÄÌÄ
´ µ
ÌÄ ¸
» ¿¿

6. ËÆ ÄÌÄ
ÄÌÄ
º
þ
º
ÄÌÄ
ÄÌÄ
¸ DSNF (f )
fº
» ¿¿

7. (p ∨ q) ∧ Gr ∧ G(p → Xq) ∧ GFp
Props Props Props Props ···
» ¿¿

8. (p ∨ q) ∧ Gr ∧ G(p → Xq) ∧ GFp
Props Props Props Props ···
I
0
» ¿¿

9. (p ∨ q) ∧ Gr ∧ G(p → Xq) ∧ GFp
Props Props Props Props ···
I U U U U
0
» ¿¿

10. (p ∨ q) ∧ Gr ∧ G(p → Xq) ∧ GFp
Props Props Props Props ···
I U U U U
0
» ¿¿

11. (p ∨ q) ∧ Gr ∧ G(p → Xq) ∧ GFp
Props Props Props Props ···
I U U U U
0
» ¿¿

12. (p ∨ q) ∧ Gr ∧ G(p → Xq) ∧ GFp
Props Props Props Props ···
I U U U U
0
» ¿¿

13. Ú Ë Ô Ö Ø ÆÓÖÑ Ð ÓÖÑ ´ ËÆ µ
½ U
¾ I
¿ S
ϕ → Xψ
E
Fl ¸
l
I ∧ GU ∧ GS ∧ GE
» ¿¿

14. (p ∨ q) ∧ Gr ∧ G(p → Xq) ∧ GFp
Props Props Props Props ···
I U U U U
I = {(q ∨ q)}
U = {r }
S = {p → Xq}
E = {Fp}
» ¿¿

15. (p ∨ q) ∧ Gr ∧ G(p → Xq) ∧ GFp
Props Props Props Props ···
I U U U U
I = {(q ∨ q)}
U = {r }
S = {p → Xq}
E = {Fp}
G
» ¿¿

16. I = {p1 }
 
 (p1 → ¬On, ¬Fault), 
press

 (p → On, ¬Fault),  
 2  2
1

 

(p3 → ¬On, Fault),
  ~On On press
U= ~Fault ~Fault
 (p1 → ¬p2 , ¬p3 ),
 

press
 (p2 → ¬p1 , ¬p3 ),

 

 

repair
(p3 → ¬p1 , ¬p2 )
 
~On
  Fault
 (p1 → Xp2 ),  3
S= (p2 → X(p1 ∨ Nextp3 )),
(p3 → Xp1 )
 
E = {FFault}
½¼ » ¿¿

17. ËÆ
ϕ DSNF (ϕ)
ü ¸ DSNF (ϕ)
½½ » ¿¿

18. ËÆ
ÆÆ
ý
ϕ DSNF (ϕ)
ü ¸ DSNF (ϕ)
½½ » ¿¿

19. ÆÆ
ÆÆ ¹
∧¸ ∨¸ ¬
¬Xϕ ≡ X¬ϕ;
¬Gϕ ≡ F¬ϕ;
¬Fϕ ≡ G¬ϕ;
¬(ϕUψ) ≡ ¬ψW(¬ϕ ∧ ¬ψ));
¬(ϕWψ) ≡ ¬ψU(¬ϕ ∧ ¬ψ).
ϕ σ
σ |= ϕ ⇐⇒ σ |= NNF (ϕ)
½¾ » ¿¿

20. ½¿ » ¿¿

21. ¸
ϕ ¸ ψ ø Fψ1 ¸ Gψ1 ¸ ψ1 Uψ2
ψ1 Wψ2
ψ
p
G(p → ψ)
½ » ¿¿

22. ½ » ¿¿

23. σ∗ σ¸
(σ, i ) |= p → (σ ∗ , i ) |= p
(σ, i ) |= ¬p → (σ ∗ , i ) |= ¬p
¸ σ∗
¸ σ º
¸ {a, ¬b, x, y } {a, ¬b}
{¬a, ¬b, x, y } {a, ¬b}º
ϕ∗ ϕ º
σ : σ |= ϕ σ∗ σ∗ |= ϕ∗
σ ∗ : σ ∗ |= ϕ∗ σ ∗ |= ϕ º
½ » ¿¿

24. G(p → Gψ1 ); G(p → Xψ1 );
G(p → ψ1 Uψ2 ); G(p → Fψ1 );
G(p → ψ1 Wψ2 );
Gψ1 ≡ ψ1 ∧ XGψ1
´
Ìĵ¸
º
º
½ » ¿¿

25. G(p → Gψ1)
ψ = G(p → Gψ1 )º
ψ ∗ = G(p → r ) ∧ G(r → Xr ) ∧ G(r → ψ1 ),
r º
σ : σ |= G(p → Gψ1 ) σ∗
σ∗ |= ψ∗
σ ∗ : σ ∗ |= ψ ∗ º
σ ∗ |= G(p → ψ1 )
(=⇒)
(σ ∗ , i ) |= r ⇐⇒ (σ, i ) |= Gψ1
(⇐=)
¸ (σ ∗ , i ) |= r (σ ∗ , i ) |= Gψ1
½ » ¿¿

26. G(p → ψ1 Uψ2 )
ψ = G(p → ψ1 Uψ2 )º
ψ ∗ =G(p → Fψ2 )
∧G(p → (ψ1 ∧ s) ∨ ψ2 )
∧G(s → X((ψ1 ∧ s) ∨ ψ2 ))
s º
σ : σ |= G(p → ψ1 Uψ2 )
σ ∗ σ ∗ |= ψ ∗
σ ∗ : σ ∗ |= ψ ∗ σ ∗ |= G(p → ψ1 Uψ2 ) º
(=⇒)
(σ ∗ , i ) |= s ⇐⇒ (σ, i ) |= (¬ψ2 ∧ ψ1 Uψ2 )
(⇐=)
¸ (σ ∗ , i ) |= (s ∧ Fψ2 ) (σ ∗ , i ) |= ψ1 Uψ2
½ » ¿¿

27. G(p → ψ1 Wψ2)
ψ = G(p → ψ1 Wψ2 )º
ψ ∗ =G(p → (ψ1 ∧ s) ∨ ψ2 )
∧G(s → X((ψ1 ∧ s) ∨ ψ2 ))
s º
σ : σ |= G(p → ψ1 Wψ2 )
σ ∗ σ ∗ |= ψ ∗
σ ∗ : σ ∗ |= ψ ∗
σ ∗ |= G(p → ψ1 Wψ2 ) º
¾¼ » ¿¿

28. ψ = G(p → Fψ1 )
º
ψ ∗ =G((p ∧ ¬ψ1 ) → w )∧
G((w ∧ X¬ψ1 ) → Xw )∧
GF¬w
w º
σ : σ |= G(p → Fψ1 ) σ∗
σ∗ |= ψ∗
σ ∗ : σ ∗ |= ψ ∗ º
σ ∗ |= G(p → Fψ1 )
¾½ » ¿¿

29. ψ = G(p → Fψ1 )
º
ψ ∗ =G((p ∧ ¬ψ1 ) → w )∧
G(w → X(ψ1 ∨ w ))∧
GF¬w
w º
σ : σ |= G(p → Fψ1 ) σ∗
σ∗ |= ψ∗
σ ∗ : σ ∗ |= ψ ∗ º
σ ∗ |= G(p → Fψ1 )
¾½ » ¿¿

30. (=⇒)
ψ = G(p → Fψ1 );
ψ ∗ = G((p ∧ ¬ψ1 ) → w ) ∧ G((w ∧ X¬ψ1 ) → Xw ) ∧ GF¬w
σ |= {G(p → Fψ1 )}º
½ σ |= GFp º
¸ σ |= GFψ1 º
(σ ∗ , i ) |= ¬w ⇔ (σ, i ) |= ψ
¾ σ |= FG¬p º
σ |= G¬p º
(σ ∗ , i) |= ¬w i ∈ Nº
j ∈ N º º (σ, j) |= p i j¸
(σ, i) |= ¬p º k j º º (σ, k) |= ψ1 º
(σ ∗ , i) |= ¬w ⇔ (σ ∗ , i) |= ψ1 i k,
(σ ∗ , i) |= ¬w i k.
¾¾ » ¿¿

31. (⇐=)
ψ = G(p → Fψ1 );
ψ ∗ = G((p ∧ ¬ψ1 ) → w ) ∧ G((w ∧ X¬ψ1 ) → Xw ) ∧ GF¬w
σ ∗ |= ψ ∗ º ¸ σ ∗ |= G(p → Fψ1 )¸ ¸
σ∗|= F(p ∧ G¬ψ1 )º
¸ m∈N (σ ∗ , m) |= p
n m¸ (σ ∗ , n) |= ¬ψ1 )º n m (σ ∗ , n) |= w º
º
¾¿ » ¿¿

32. ¾ » ¿¿

33. DSNF = U, I, S, E º sig (DSNF ) = Prop º
þ G Prop
L(v ) |= U º
þ v v′
(P → XQ) ∈ S ¸ L(v ) |= P L(v ′ ) |= Q º
þ v G L(v ) |= I ∪ U º
H DSNF
G¸ ¸
º
¾ » ¿¿

34. I= a ∧ ¬l  
 a ∧ ¬l → X((a ∧ ¬l ) ∨ (a ∧ l )) 
U =∅ S= a ∧ l → X(¬a ∧ ¬l )
¬a ∧ ¬l → X(¬a ∧ ¬l )
 
E= Fl
ÈË Ö Ö ÔÐ
Ñ ÒØ×
v0 v1 v2
L(v0 ) = {a, ¬l }; L(v1 ) = {a, l }; L(v2 ) = {¬a, ¬l }º
¾ » ¿¿

35. HR ¸
H v ¸
v
¹ Fl ∈ E ¸ v v′
¸ L(v ′ ) |= l º
¾ » ¿¿

36. I= a ∧ ¬l  
 a ∧ ¬l → X((a ∧ ¬l ) ∨ (a ∧ l )) 
U =∅ S= a ∧ l → X(¬a ∧ ¬l )
¬a ∧ ¬l → X(¬a ∧ ¬l )
 
E= Fl
Ñ ÒØ×
v0 v1 v2
L(v0 ) = {a, ¬l }; L(v1 ) = {a, l }; L(v2 ) = {¬a, ¬l }º
¾ » ¿¿

37. I= a ∧ ¬l  
 a ∧ ¬l → X((a ∧ ¬l ) ∨ (a ∧ l )) 
U =∅ S= a ∧ l → X(¬a ∧ ¬l )
¬a ∧ ¬l → X(¬a ∧ ¬l )
 
E= Fl
Ñ ÒØ×
v0 v1
L(v0 ) = {a, ¬l }; L(v1 ) = {a, l }; L(v2 ) = {¬a, ¬l }º
¾ » ¿¿

38. I= a ∧ ¬l  
 a ∧ ¬l → X((a ∧ ¬l ) ∨ (a ∧ l )) 
U =∅ S= a ∧ l → X(¬a ∧ ¬l )
¬a ∧ ¬l → X(¬a ∧ ¬l )
 
E= Fl
Ñ ÒØ×
v0
L(v0 ) = {a, ¬l }; L(v1 ) = {a, l }; L(v2 ) = {¬a, ¬l }º
¾ » ¿¿

39. I= a ∧ ¬l  
 a ∧ ¬l → X((a ∧ ¬l ) ∨ (a ∧ l )) 
U =∅ S= a ∧ l → X(¬a ∧ ¬l )
¬a ∧ ¬l → X(¬a ∧ ¬l )
 
E= Fl
L(v0 ) = {a, ¬l }; L(v1 ) = {a, l }; L(v2 ) = {¬a, ¬l }º
¾ » ¿¿

41. σ |= DSNF (ϕ) π HR
σ(i ) = π(i )º
π HR ¸
¸
l Fl ∈ E ¸ π
º π |= DSNF (ϕ)
DSNF (ϕ)
¸ HR º
¾ » ¿¿

42. S = (Q, T , q0 , L)
ϕ ÄÌĹ DSNF (ϕ) = U, I, S, E
¸ HR
º
SDSNF (ϕ) = (QDSNF , TDSNF , QDSNFI , LDSNF )
S |= ϕ ⇐⇒ σ S π
SDSNF (ϕ) ¸ π σ π
º
¿¼ » ¿¿

43. S = (Q, T , q0 , L) ÄÌÄ ϕº
ϕ
SDSNF (¬ϕ) = (QDSNF , TDSNF , Q0DSNF , LDSNF )
S ∗ (Q ∗ , T ∗ , Q0 , L∗ ) = S × SD
∗
Q ∗ = {(q, qD ) | LD (qD ) L(q)},
∗ ′ ′ ′ ′
T = {(q, qD ) → (q , qD ) | (q → q ) ∈ T , (qD → qD ) ∈ Td },
∗
Q0 = {(q0 , q0D ) | q0D ∈ Q0D },
L∗ (q, qD ) = LD (qD ).
C ´ Eµ
S∗
¸ S
¬ϕº
¿½ » ¿¿

44. S∗
¸ S
¬ϕ
ÌÄ EGTrue
º
O(|S| · 2|ϕ| )
¿¾ » ¿¿