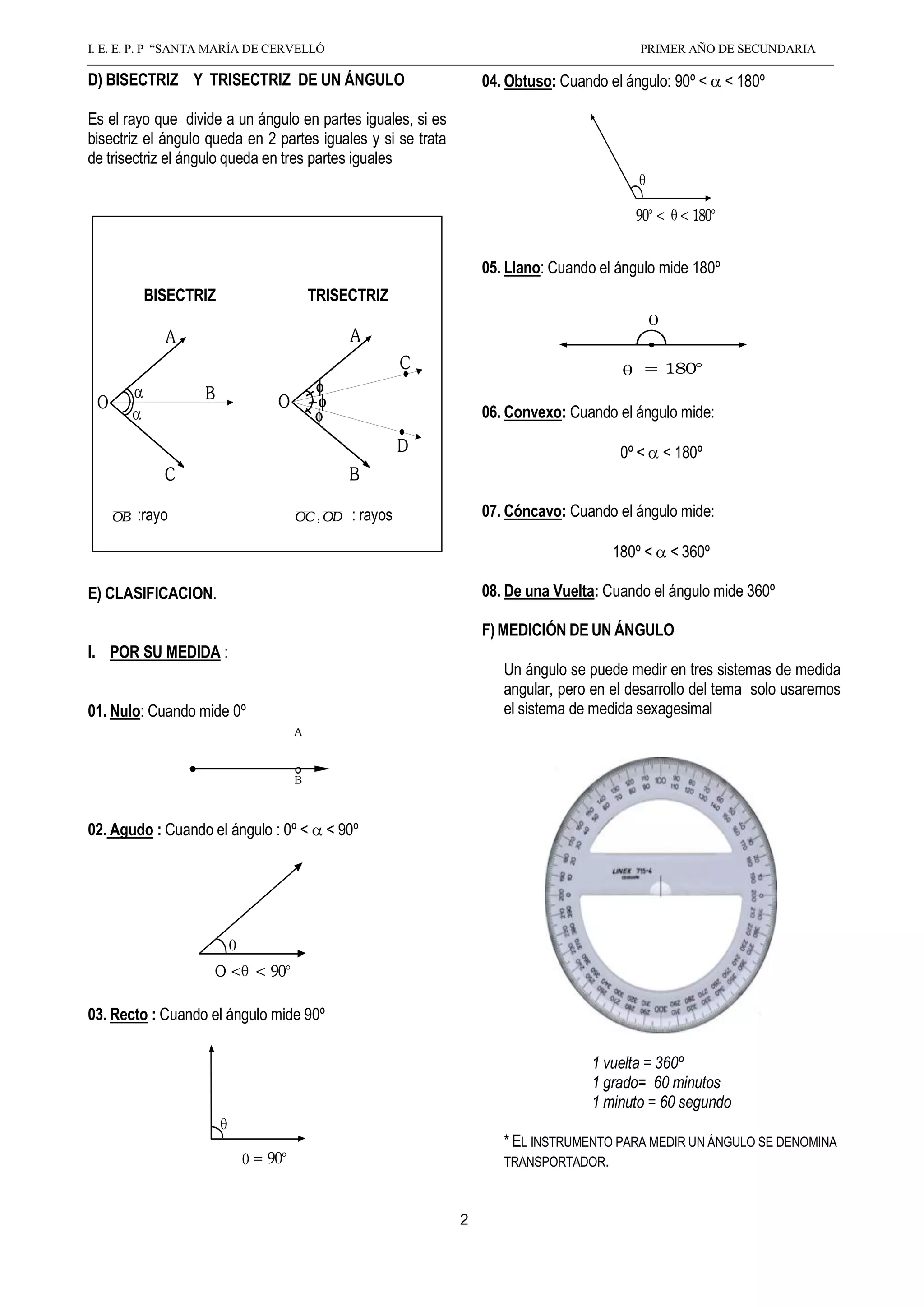
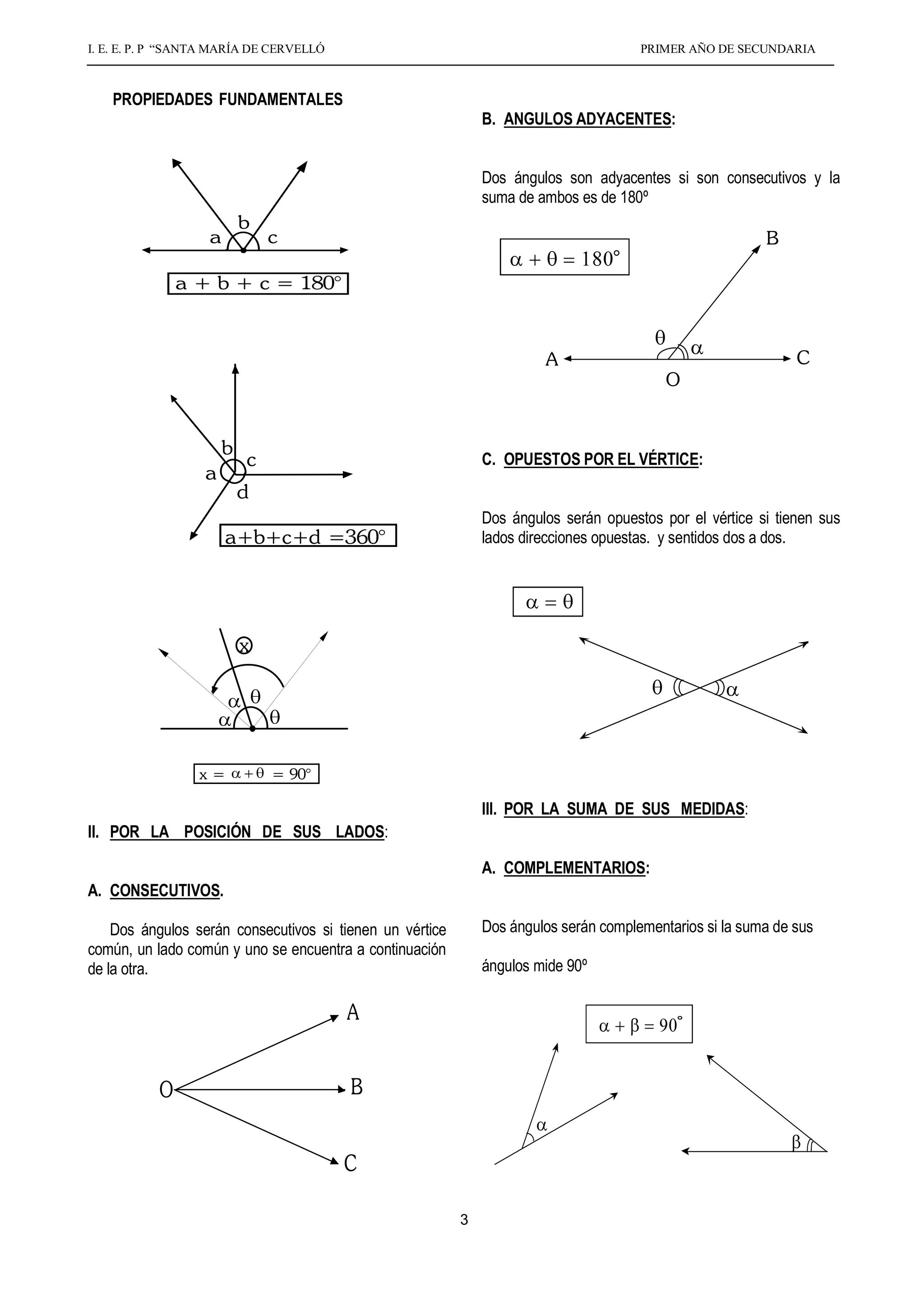
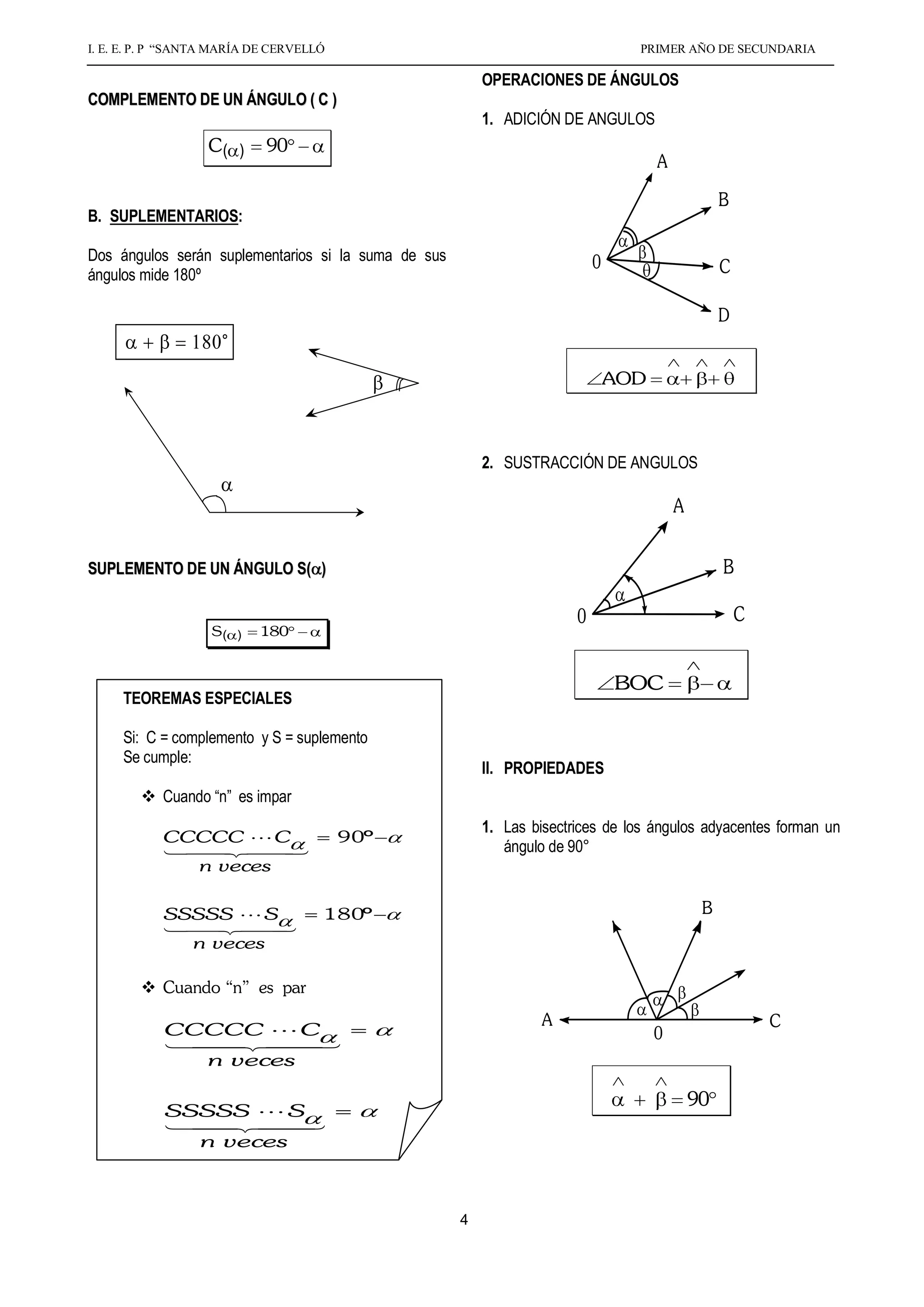
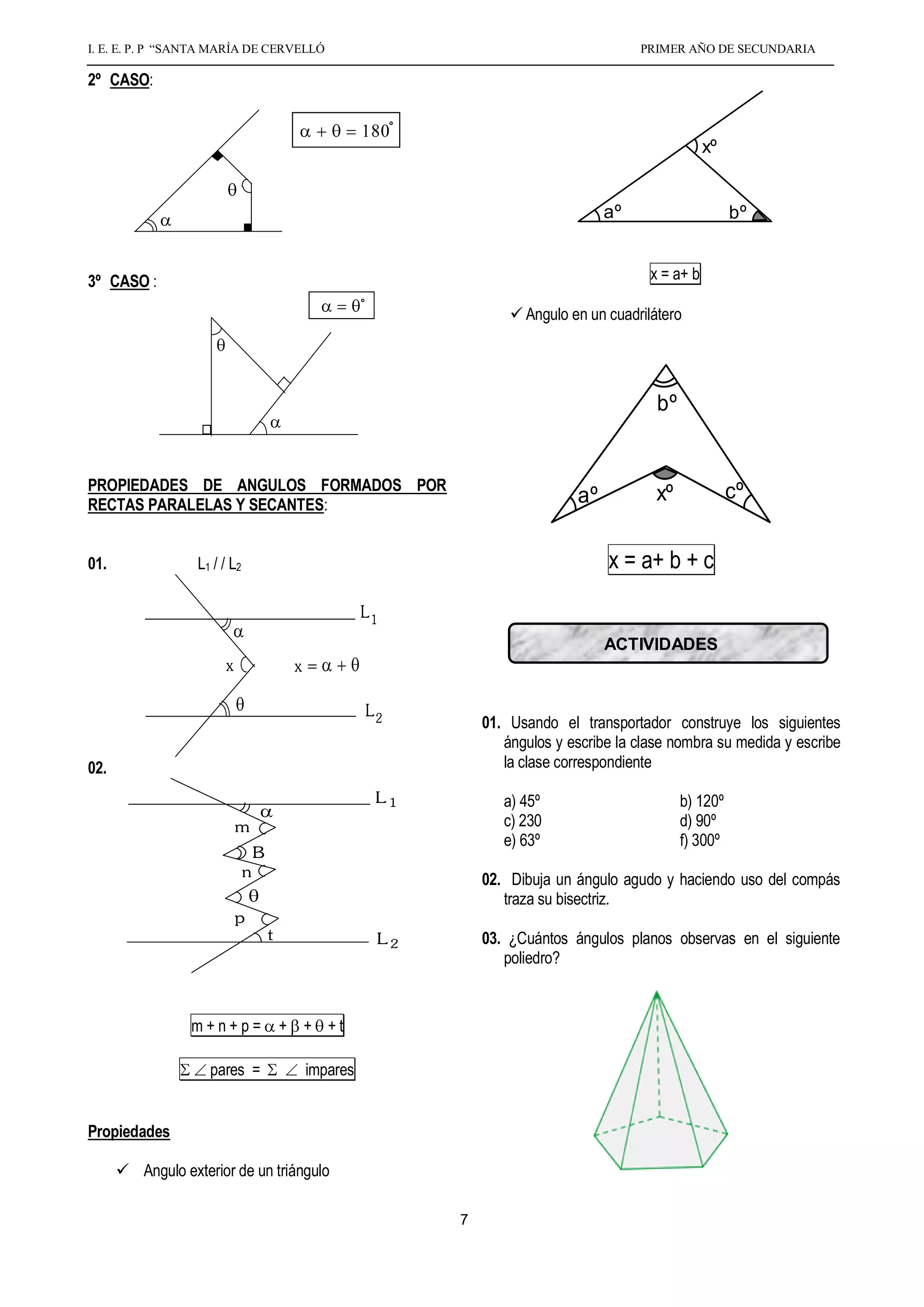
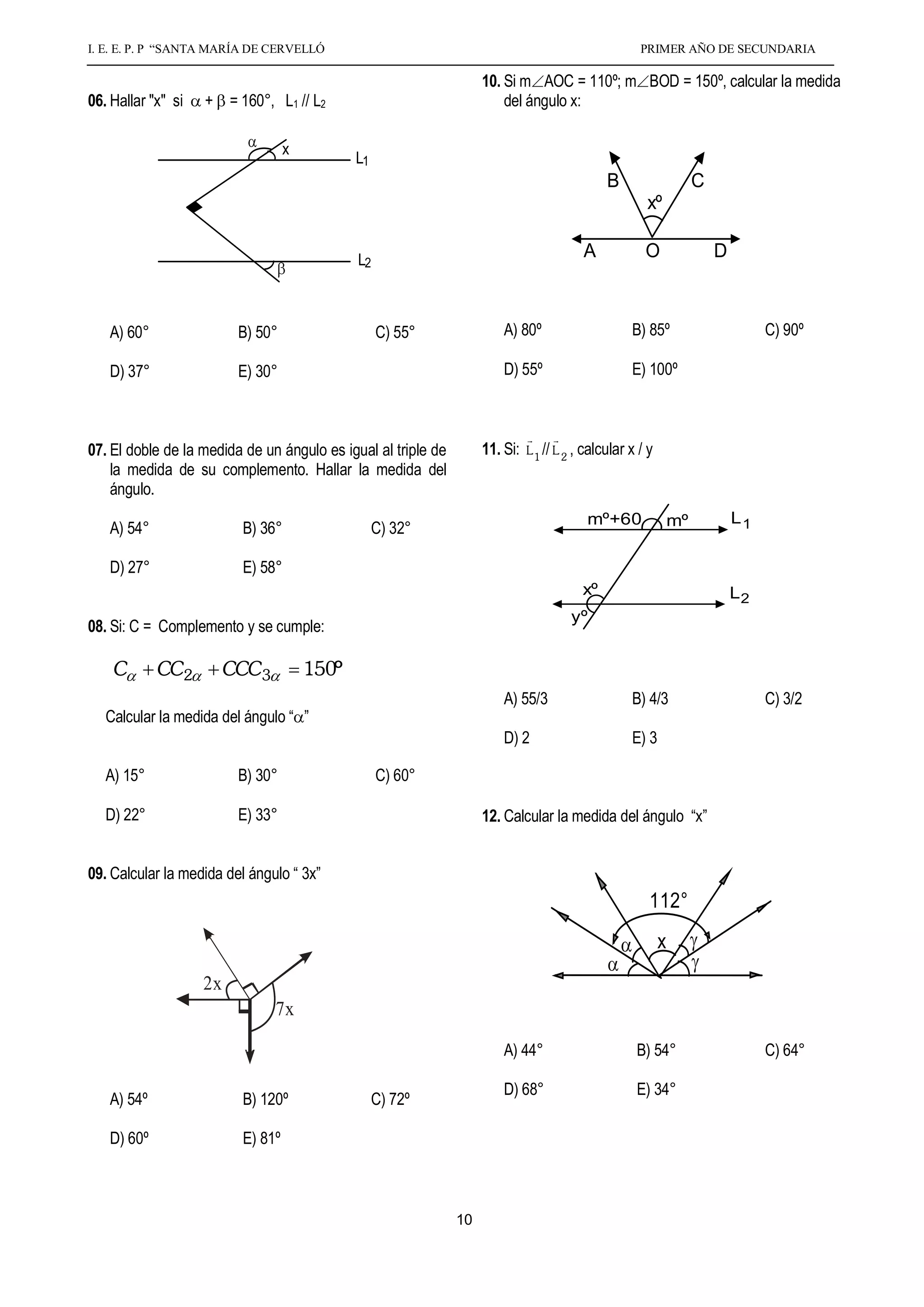
El documento presenta información sobre ángulos planos, incluyendo su definición, elementos, clasificación, medición, propiedades y operaciones. Define un ángulo como la inclinación mutua de dos líneas que se encuentran en un plano y no están en línea recta. Explica los tipos de ángulos (agudo, recto, obtuso, etc.), y cómo medir ángulos usando el sistema sexagesimal de grados, minutos y segundos. También cubre propiedades de ángulos adyacentes, opuestos por el vértice, complementarios

1. I. E. E. P. P “SANTA MARÍA DE CERVELLÓ PRIMER AÑO DE SECUNDARIA
NUEVO CHIMBOTE
El transportador
MARCO TEORICO
COMENTARIO PREVIO
ANGULOS
Euclides define un ángulo como la inclinación mutua de
dos líneas que se encuentran una a otra en un plano y no La idea de ángulo aparece en muchas situaciones de
están en línea recta. Según Proclus un ángulo debe ser nuestra vida diaria, por ejemplo cuando abrimos un
una calidad o una cantidad, o una relación. El primer compás, unas tijeras, el cruce de las veredas de dos
concepto fue utilizado por Eudemus, que describió un calles las ramas de un árbol, las estructura de una
ángulo como desviación de una línea recta; el segundo bicicleta etc.
por Carpus de Antioch, que lo vio como el intervalo o el
espacio entre las líneas que se intersecaban; Euclides
adoptó un tercer concepto, aunque sus definiciones de A) DEFINICIÓN: Es una región en el plano determinado
ángulos rectos, agudos, y obtusos son cuantitativas. por dos rayos que tienen un mismo origen. Dicho
origen es el vértice del ángulo y los rayos son sus
Se denomina ángulo plano a la porción de plano (común) lados.
comprendida entre dos semirrectas con un origen en
común denominado vértice. Otra concepción de ángulo
dice que éste es la figura formada por dos rayos con A
origen común. Para ambos casos el ángulo no se puede
Notación :
medir (son subconjuntos de puntos del plano, por lo tanto AOB, AOB
infinitos), solo se puede medir la abertura del ángulo.
Las unidades utilizadas para la medida de los ángulos O
del plano son:
Lados
El Radián ( rad. usado oficialmente en S. I)
(vértice)
El Grado centesimal ( º ) B
El Grado sexagesimal( g )
Los ángulos se pueden medir mediante utensilios tales
como el goniómetro, el cuadrante, el sextante, la B) ELEMENTOS
ballestina, el transportador de ángulos o semicírculo
graduado, etc. y el lápiz.
O : vértice
OA y OB : lados
C) NOTACIÓN
AOB : Se lee “ángulo AOB”
α : Se lee ángulo alfa
El transportador
1

2. I. E. E. P. P “SANTA MARÍA DE CERVELLÓ PRIMER AÑO DE SECUNDARIA
D) BISECTRIZ Y TRISECTRIZ DE UN ÁNGULO 04. Obtuso: Cuando el ángulo: 90º < < 180º
Es el rayo que divide a un ángulo en partes iguales, si es
bisectriz el ángulo queda en 2 partes iguales y si se trata
de trisectriz el ángulo queda en tres partes iguales
90° < < 180°
O < < 90° = 90° = 180°
05. Llano: Cuando el ángulo mide 180º
BISECTRIZ TRISECTRIZ
A A
< 90° C
90° < < 180° = 180°
= 90°
B O
O
06. Convexo: Cuando el ángulo mide:
D 0º < < 180º
C B
OB :rayo OC , OD : rayos 07. Cóncavo: Cuando el ángulo mide:
180º < < 360º
E) CLASIFICACION. 08. De una Vuelta: Cuando el ángulo mide 360º
F) MEDICIÓN DE UN ÁNGULO
I. POR SU MEDIDA :
Un ángulo se puede medir en tres sistemas de medida
angular, pero en el desarrollo del tema solo usaremos
01. Nulo: Cuando mide 0º el sistema de medida sexagesimal
A
B
02. Agudo : Cuando el ángulo : 0º < < 90º
90° < < 180°
O < < 90° = 90° = 180°
03. Recto : Cuando el ángulo mide 90º
1 vuelta = 360º
1 grado= 60 minutos
1 minuto = 60 segundo
90° < < 180° * EL INSTRUMENTO PARA MEDIR UN ÁNGULO SE DENOMINA
O < < 90° = 90° = 180°
TRANSPORTADOR.
2

3. I. E. E. P. P “SANTA MARÍA DE CERVELLÓ PRIMER AÑO DE SECUNDARIA
PROPIEDADES FUNDAMENTALES
B. ANGULOS ADYACENTES:
Dos ángulos son adyacentes si son consecutivos y la
suma de ambos es de 180º
b b
a c c B
a
d
a + b + c = 180°
a+b+c+d =360°
A C
O
b
c C. OPUESTOS POR EL VÉRTICE:
a
d
0°
Dos ángulos serán opuestos por el vértice si tienen sus
a+b+c+d =360° lados direcciones opuestas. y sentidos dos a dos.
x
x= = 90°
x
x= = 90°
III. POR LA SUMA DE SUS MEDIDAS:
II. POR LA POSICIÓN DE SUS LADOS:
A. COMPLEMENTARIOS:
A. CONSECUTIVOS.
Dos ángulos serán consecutivos si tienen un vértice Dos ángulos serán complementarios si la suma de sus
común, un lado común y uno se encuentra a continuación
de la otra. ángulos mide 90º
A
O B
C
3

4. I. E. E. P. P “SANTA MARÍA DE CERVELLÓ PRIMER AÑO DE SECUNDARIA
OPERACIONES DE ÁNGULOS
COMPLEMENTO DE UN ÁNGULO ( C )
1. ADICIÓN DE ANGULOS
C( ) 90
A
B
B. SUPLEMENTARIOS:
Dos ángulos serán suplementarios si la suma de sus 0
ángulos mide 180º C
D
AOD
2. SUSTRACCIÓN DE ANGULOS
A
SUPLEMENTO DE UN ÁNGULO S( ) B
0 C
S( ) 180
BOC
TEOREMAS ESPECIALES
Si: C = complemento y S = suplemento
Se cumple:
II. PROPIEDADES
 Cuando “n” es impar
1. Las bisectrices de los ángulos adyacentes forman un
CCCCC  C 90º
 
  ángulo de 90°
n veces
SSSSS  S 180º B
 
 
n veces
 Cuando “n” es par
A C
CCCCC  C 0
 
 
n veces
90
SSSSS  S
 
 
n veces
4

5. I. E. E. P. P “SANTA MARÍA DE CERVELLÓ PRIMER AÑO DE SECUNDARIA
2. Las bisectrices de dos ángulos complementarios b. Rectas Perpendiculares ( ) : Aquellas que
forman un ángulo de 45° forman ángulos iguales a 90º.
A
L
B
L
P (común)
C
0
COROLARIOS
45 01. Dos rectas paralelas a una tercera son paralelas entre
si .
Si : L1 // L y L2 // L L1 // L2
ANGULOS ENTRE RECTAS .
L1
1. Rectas Paralelas . Dos rectas serán paralelas si no L
tienen ningún punto en común.
L2
L1
02. Si dos rectas son paralelas una recta perpendicular a
L2 una de ellas será también perpendicular a la otra.
Si L1 // L2 y L1 L  L L2
L
L1
2. Rectas secantes. Dos rectas serán secantes si tienen
un punto en común entre ellas. L2
a. Rectas Oblicuas: Son aquellas rectas que forman
ángulos diferentes de 90º. POSTULADO DE EUCLIDES:
Por un punto exterior a una recta sólo puede pasar una
paralela de dicha recta.
L2
P
L1
L
L1
P (Común)
L / / L1 Sólo una
5

6. I. E. E. P. P “SANTA MARÍA DE CERVELLÓ PRIMER AÑO DE SECUNDARIA
1º CASO :
ANGULOS FORMADOS POR L4 L3
RECTAS PARALELAS Y
SECANTES
Si se trazan dos rectas paralelas y una recta secante L2
se formaría la gráfica dada y los siguientes ángulos
L1
internos (3, 4, 5, y 6) y los externos (1, 2, 8 y 7)
2º CASO :
1 2 L1 L2
L1
4 3
5 6 L3
L2
8 7
L4
Si L1 / / L2 y L3 / / L4
PROPIEDADES
+ = 180º
* ANGULOS CORRESPONDIENTES (Iguales)
 1= 5 3º CASO :
L3
 2= 6
L2
 4= 8
 3= 7
* ANGULOS ALTERNOS (Iguales) L1
L4
 Internos 3= 5 ; 4= 6 L1 / / L2 y L3 / / L4
 Externos 1= 7 ; 2= 8
=
* ANGULOS CONGUGADOS (Suplementarios)
ANGULOS DE LADOS PERPENDICULARES
 Internos 3 + 6 = 180º ;
4 + 5 = 180º 1º CASO:
 Externos 1 + 8 = 180º ;
2 + 7 = 180º
ANGULOS DE LADOS PARALELOS
=
6

7. I. E. E. P. P “SANTA MARÍA DE CERVELLÓ PRIMER AÑO DE SECUNDARIA
2º CASO:
xº
aº bº
3º CASO : x = a+ b
 Angulo en un cuadrilátero
bº
PROPIEDADES DE ANGULOS FORMADOS POR cº
RECTAS PARALELAS Y SECANTES: aº xº
01. L1 / / L2 x = a+ b + c
L1
ACTIVIDADES
x x=
L2
01. Usando el transportador construye los siguientes
ángulos y escribe la clase nombra su medida y escribe
02. la clase correspondiente
L1 a) 45º b) 120º
m c) 230 d) 90º
e) 63º f) 300º
B
n 02. Dibuja un ángulo agudo y haciendo uso del compás
traza su bisectriz.
p
t L2 03. ¿Cuántos ángulos planos observas en el siguiente
poliedro?
m+n+p= + + +t
pares = impares
Propiedades
 Angulo exterior de un triángulo
7

8. I. E. E. P. P “SANTA MARÍA DE CERVELLÓ PRIMER AÑO DE SECUNDARIA
04. Calcular el complemento de los ángulos: 05. Calcular “x” en la siguiente figura, siendo A una recta.
a) 46º b) 60º
b) nº d) nº + 10º
05. Calcular el suplemento de los ángulos
22º 88º
a) 120º b) 100º
3xº+8º A
b) a º d) a º + 24º
A) 20º B) 28º C) 30º
PROBLEMAS DE CLASE D) 40º E) 32º
06. Calcular el complemento de “x” si los ángulos
01. Uno de los ángulos suplementarios en 30º más que el mostrados son opuestos por el vértice.
otro ángulo. Calcular el complemento del ángulo
menor.
70º xº + 30º
A) 20º B) 25º C) 15º
D) 40º E) 32º
A) 40º B) 50º C) 30º
02. La diferencia de dos ángulos complementarios es 24º.
Determinar la medida del ángulo menor. D) 60º E) 80º
A) 57º B) 33º C) 30º 07. Hallar el suplemento de “x”
D) 40º E) N. A
03. Calcular el suplemento del complemento del 2x 3x 2x
suplemento de un ángulo que mide 120º
A) 150º B) 28º C) 30º A) 164º B) 162º C) 172º
D) 120º E) N. A D) 174º E) 124º
04. Dos ángulos suplementarios están en relación de 7 a 08. Calcular “ ”, si m // n:
11. Calcular la medida del ángulo menor
m
A) 10º B) 110º C) 70º +10
D) 40º E) N. A n +30º
8

9. I. E. E. P. P “SANTA MARÍA DE CERVELLÓ PRIMER AÑO DE SECUNDARIA
12. Si, S = Suplemento y C = Complemento
A) 30º B) 20º C) 16º Calcular:
D) 18º E) 28º
SSSS  S150 º CCCC  C50 º SSSCCSSC 40 º
 
   
 
155 veces 156 veces
09. La diferencia entre el suplemento y el complemento de
es igual al séxtuplo de . Calcular el valor del
A) 150º B) 160º C) 140º
ángulo “ ”.
D) 130º E) 200º
A) 16° B) 15° C) 11°
D) 30° E) N. A
PROBLEMAS PROPUESTOS
10 Si: L1 // L2; hallar x.
01. Uno de los ángulos suplementarios en 10º más que el
otro ángulo. Calcular el complemento del ángulo del
L1
20° ángulo mayor.
300°
x° A) 50º B) 25º C) 15º
310° D) 40º E) 32º
10° L2
02. La diferencia de dos ángulos complementarios es 20º.
Determinar la medida del ángulo menor.
A) 60° B) 70° C) 80°
A) 55º B) 35º C) 30º
D) 90° E) 30°
D) 40º E) N. A
03. Calcular el suplemento del complemento del
11. En el esquema adjunto, calcular el ángulo "x", siendo:
suplemento de un ángulo que mide 100º
° - °= 10°
A) 150º B) 28º C) 30º
D) 170º E) N. A
04. Dos ángulos suplementarios están en relación de 3 a
x° 15. Calcular la medida del ángulo menor
A) 10º B) 150º C) 30º
D) 40º E) N. A
05. La suma del complemento más el suplemento de cierto
A) 50° B) 40° C) 20° ángulo es igual a 130º. Hallar la medida de dicho
ángulo.
D) 10° E) 5°
A) 50º B) 60º C) 70º
D) 80º E) 90º
9

10. I. E. E. P. P “SANTA MARÍA DE CERVELLÓ PRIMER AÑO DE SECUNDARIA
10. Si m AOC = 110º; m BOD = 150º, calcular la medida
06. Hallar "x" si + = 160°, L1 // L2 del ángulo x:
x
L1
B C
xº
L2 A O D
A) 60° B) 50° C) 55° A) 80º B) 85º C) 90º
D) 37° E) 30° D) 55º E) 100º
 
07. El doble de la medida de un ángulo es igual al triple de 11. Si: L 1 // L 2 , calcular x / y
la medida de su complemento. Hallar la medida del
ángulo.
mº+60 mº L1
A) 54° B) 36° C) 32°
D) 27° E) 58°
xº L2
yº
08. Si: C = Complemento y se cumple:
C CC2 CCC3 150º
A) 55/3 B) 4/3 C) 3/2
Calcular la medida del ángulo “ ”
D) 2 E) 3
A) 15° B) 30° C) 60°
D) 22° E) 33° 12. Calcular la medida del ángulo “x”
09. Calcular la medida del ángulo “ 3x”
112°
x
X
3x 2x xº - 70º 50º
7x
A) 44° B) 54° C) 64°
D) 68° E) 34°
A) 54º B) 120º C) 72º
D) 60º E) 81º
10