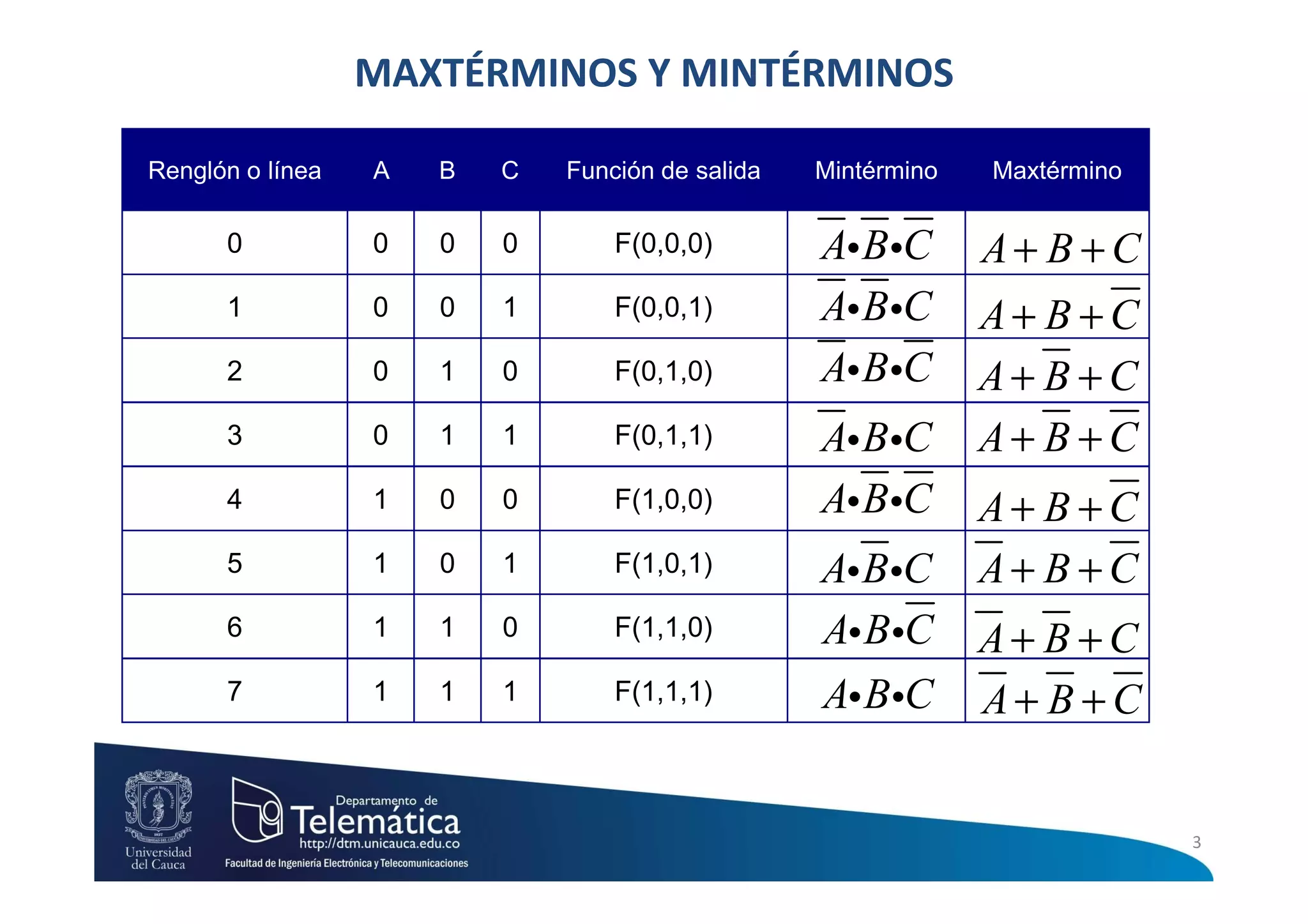
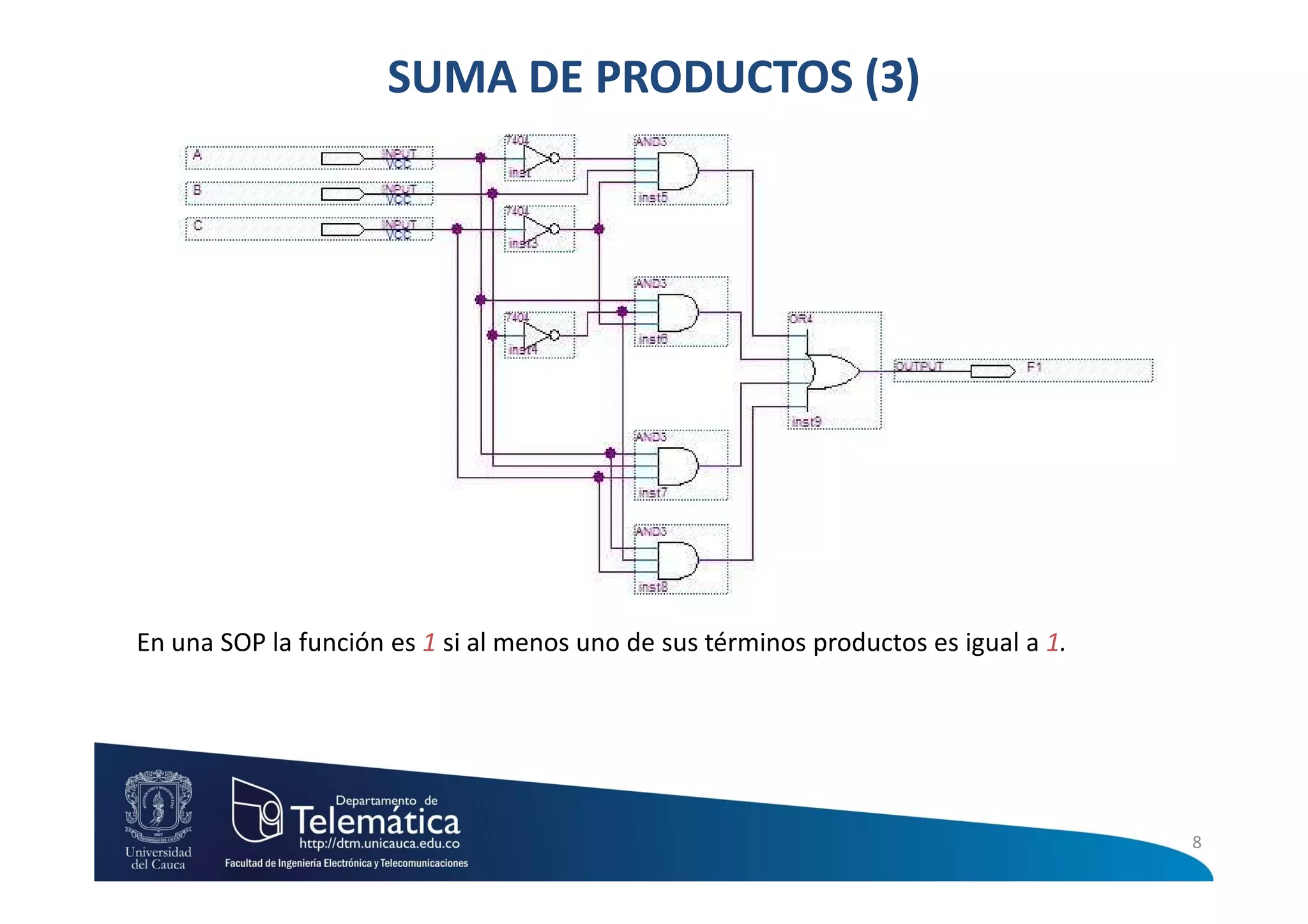
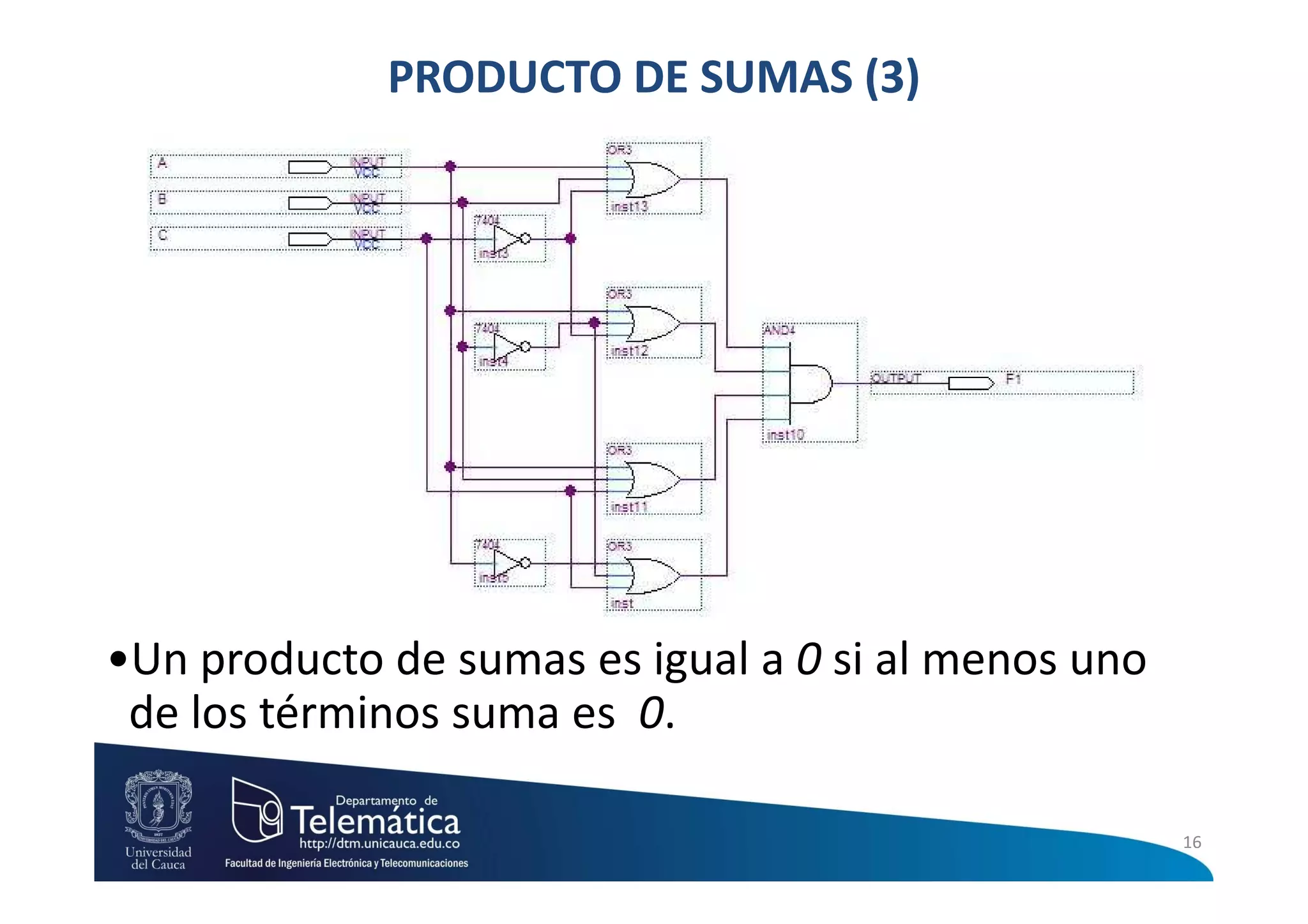
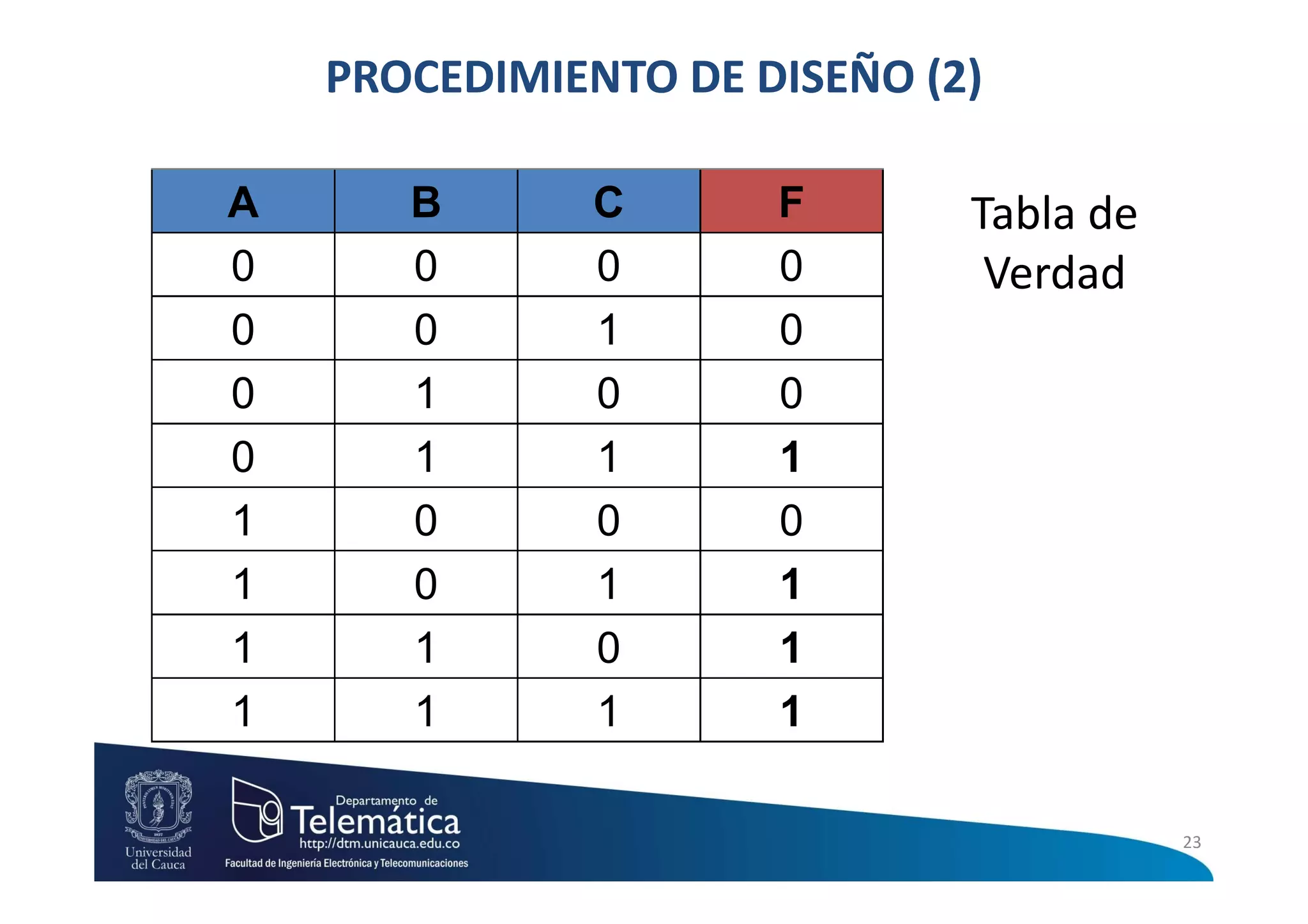
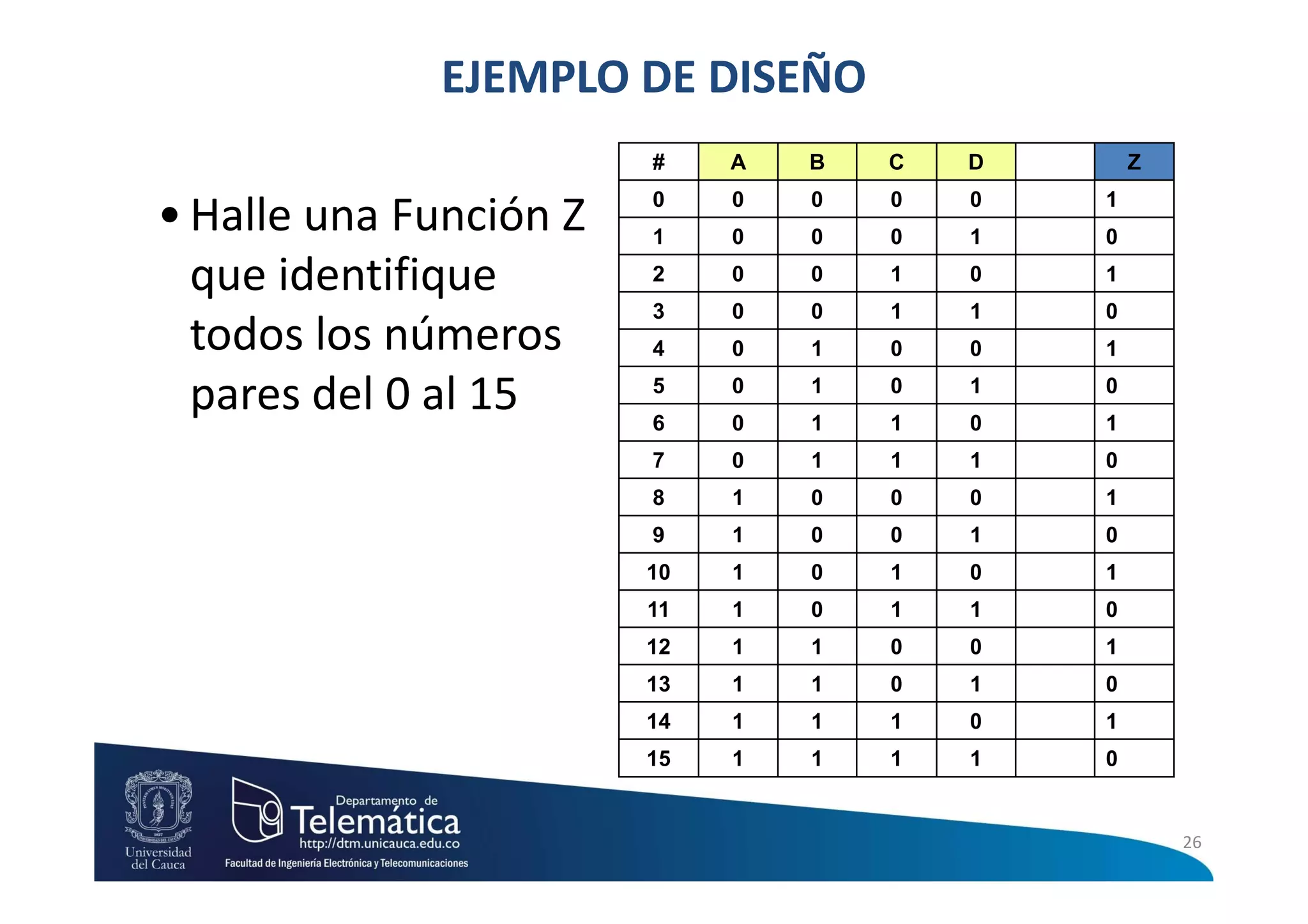
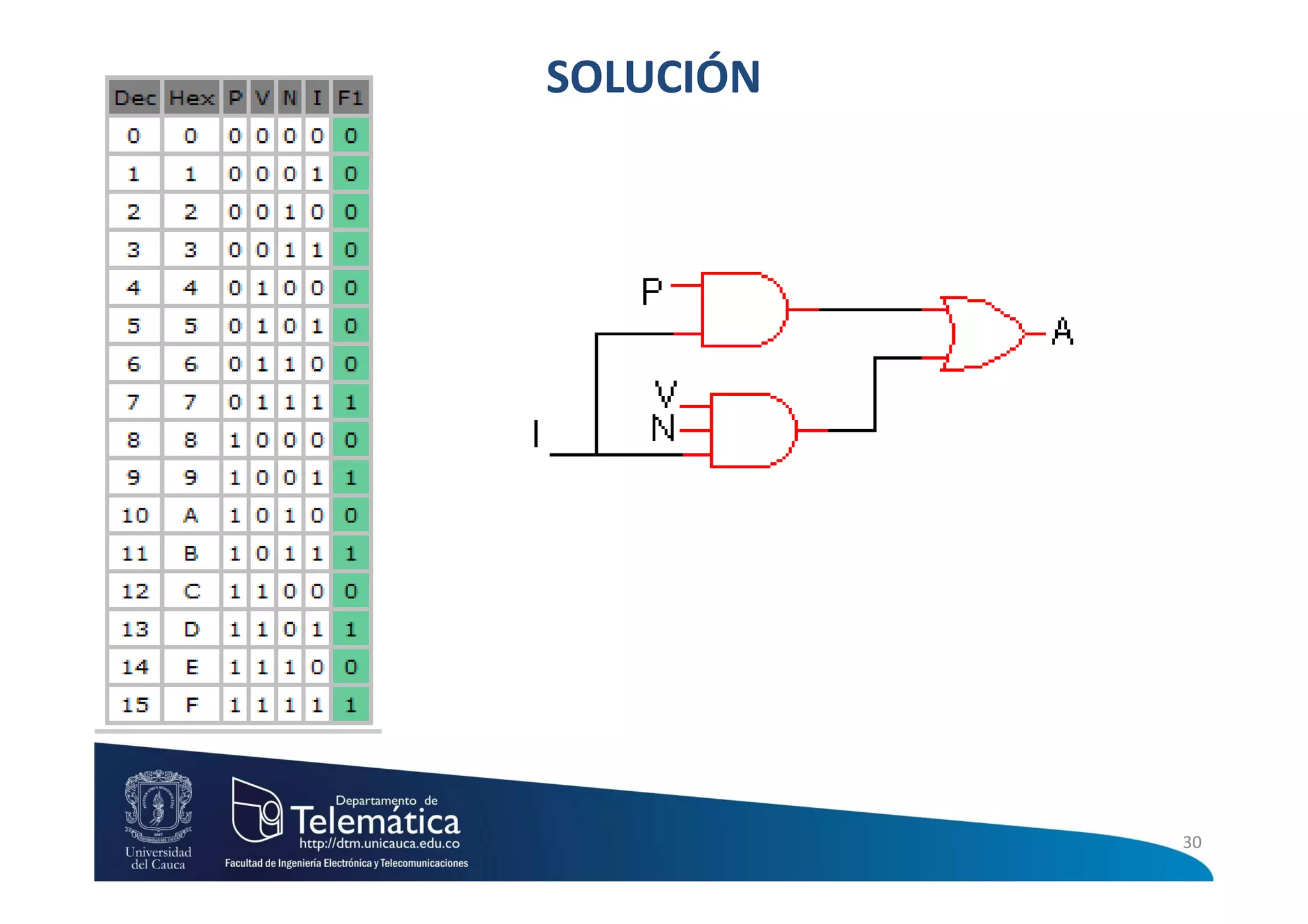
Este documento presenta información sobre circuitos digitales combinacionales. Explica que un circuito combinacional es aquel cuyas salidas en un instante son función exclusivamente de las entradas en ese mismo instante. También define conceptos como máximos términos, mínimos términos, sumas de productos y productos de sumas para representar funciones lógicas. Finalmente, describe el procedimiento para diseñar circuitos lógicos combinacionales que incluye elaborar la tabla de verdad, aplicar sumas de productos o productos de sumas y simplificar la

1. CIRCUITOS DIGITALES I
CIRCUITOS COMBINACIONALES
ING. FERNANDO APARICIO URBANO MOLANO

2. ANÁLISIS DE CIRCUITOS COMBINACIONALES
Un circuito combinacional es un circuito digital cuyas
salidas, en un instante determinado y sin considerar
los tiempos de propagación de las puertas, son
función, exclusivamente, de la “combinación” de
valores binarios de las entradas del circuito en ese
mismo instante.
Fout ( A, B, C , D ) = A ⋅ B + C ⋅ D
2

3. MAXTÉRMINOS Y MINTÉRMINOS
Renglón o línea A B C Función de salida Mintérmino Maxtérmino
0 0 0 0 F(0,0,0) Ai BiC A+ B +C
1 0 0 1 F(0,0,1) Ai BiC A+ B +C
2 0 1 0 F(0,1,0) Ai BiC A+ B +C
3 0 1 1 F(0,1,1) Ai BiC A+ B +C
4 1 0 0 F(1,0,0) Ai BiC A+ B +C
5 1 0 1 F(1,0,1) Ai BiC A+ B +C
6 1 1 0 F(1,1,0) Ai BiC A+ B +C
7 1 1 1 F(1,1,1) Ai BiC A+ B +C
3

4. MAXTÉRMINOS Y MINTÉRMINOS (2)
Mintérmino: Es un término de producto con n
literales en el cual hay n variables. De n variables
obtenemos 2n mintérminos.
Ej : X ⋅ Y ⋅ Z representa el 7 (con los unos)
Maxtérmino: Es un término de suma con n literales
en el cual hay n variables. De n variables obtenemos
2n maxtérminos.
Ej: X + Y + Z representa el 2 (con los ceros)
4

5. FORMAS ESTANDAR DE EXPRESIONES BOOLEANAS
Suma de productos (SOP): Suma lógica de términos
productos:
f(a,b,c) = a b c + a b c + a b c + c
Producto de sumas (POS): Producto lógico de términos
suma
f(a, b, c, d, e) = ( a + b + c)(a + d + e)(a + b + d)(d + e)
No necesariamente aparecen todas las variables de la
función.
5

6. SUMA DE PRODUCTOS
• Es la suma de los mintérminos correspondientes a las
líneas de la tabla de verdad donde la función produce una
salida igual a 1.
A B C F1
0 0 0 0 0
1 0 0 1 0
2 0 1 0 1
3 0 1 1 0
4 1 0 0 1
5 1 0 1 1
6 1 1 0 0
7 1 1 1 1
6

7. SUMA DE PRODUCTOS (2)
•La función lógica es la combinacion de los
mintérminos 010 (2), 100 (4), 101 (5) y 111 (7)
como:
F1 ( A, B, C ) = ∑ m ( 2, 4,5, 7 ) = ABC + ABC + ABC + ABC
•Cada mintérmino representa una compuerta AND
de tres entradas
•F1 es la operación OR de las salidas de las cuatro
compuertas AND.
7

8. SUMA DE PRODUCTOS (3)
En una SOP la función es 1 si al menos uno de sus términos productos es igual a 1.
8

9. EXPRESIÓN LÓGICA A SOP
A+ A =1
• Los términos producto que no contengan
alguna de las variables multiplicarlos por un
término X + X
F ( A, B, C ) = A ⋅ B ⋅ C + B ⋅ C + A
9

10. EXPRESIÓN LÓGICA A SOP
A+ A =1
• Los términos producto que no contengan
alguna de las variables multiplicarlos por un
término X + X
F ( A, B, C ) = A ⋅ B ⋅ C + B ⋅ C + A
( ) (
F ( A, B, C ) = A ⋅ B ⋅ C + A + A ⋅ B ⋅ C + A ⋅ C + C )
10

11. EXPRESIÓN LÓGICA A SOP
A+ A =1
• Los términos producto que no contengan
alguna de las variables multiplicarlos por un
término X + X
F ( A, B, C ) = A ⋅ B ⋅ C + B ⋅ C + A
( ) (
F ( A, B, C ) = A ⋅ B ⋅ C + A + A ⋅ B ⋅ C + A ⋅ C + C )
F ( A, B, C ) = A ⋅ B ⋅ C + A ⋅ B ⋅ C + A ⋅ B ⋅ C + A ⋅ C + A ⋅ C
11

12. EXPRESIÓN LÓGICA A SOP
A+ A =1
• Los términos producto que no contengan
alguna de las variables multiplicarlos por un
término X + X
F ( A, B, C ) = A ⋅ B ⋅ C + B ⋅ C + A
( )
F ( A, B, C ) = A ⋅ B ⋅ C + A + A ⋅ B ⋅ C + A ⋅ C + C ( )
F ( A, B, C ) = A ⋅ B ⋅ C + A ⋅ B ⋅ C + A ⋅ B ⋅ C + A ⋅ C + A ⋅ C
F ( A, B, C ) = A ⋅ B ⋅ C + A ⋅ B ⋅ C + A ⋅ B ⋅ C + A ⋅ C ⋅ ( B + B) + A ⋅ C ⋅ ( B + B)
12

13. EXPRESIÓN LÓGICA A SOP
A+ A =1
• Los términos producto que no contengan
alguna de las variables multiplicarlos por un
término X + X
F ( A, B, C ) = A ⋅ B ⋅ C + B ⋅ C + A
( )
F ( A, B, C ) = A ⋅ B ⋅ C + A + A ⋅ B ⋅ C + A ⋅ C + C ( )
F ( A, B, C ) = A ⋅ B ⋅ C + A ⋅ B ⋅ C + A ⋅ B ⋅ C + A ⋅ C + A ⋅ C
F ( A, B, C ) = A ⋅ B ⋅ C + A ⋅ B ⋅ C + A ⋅ B ⋅ C + A ⋅ C ⋅ ( B + B) + A ⋅ C ⋅ ( B + B)
F ( A, B, C ) = A ⋅ B ⋅ C + A ⋅ B ⋅ C + A ⋅ B ⋅ C + A ⋅ B ⋅ C + A ⋅ B ⋅ C + A ⋅ C ⋅ B
13

14. PRODUCTO DE SUMAS
• Multiplicación de los maxtérminos correspondientes a la
tabla de verdad donde la función produce una salida
igual a 0.
A B C F4
0 0 0 0 0
1 0 0 1 0
2 0 1 0 1
3 0 1 1 0
4 1 0 0 1
5 1 0 1 1
6 1 1 0 0
7 1 1 1 1
14

15. PRODUCTO DE SUMAS (2)
•La función se expresa con un maxtérmino para cada
combinación de variables que producen un 0 a la salida:
000 (0), 001 (1), 011 (3) y 110 (6) como:
( )( )(
F1 ( A, B, C ) = ∏ M ( 0,1,3, 6 ) = ( A + B + C ) ⋅ A + B + C ⋅ A + B + C ⋅ A + B + C )
•Cada maxtérmino es una compuerta OR de tres entradas y
la función es la operación AND a las salidas de las cuatro
compuertas OR.
15

16. PRODUCTO DE SUMAS (3)
•Un producto de sumas es igual a 0 si al menos uno
de los términos suma es 0.
16

17. EXPRESIONES PARA IMPLEMENTACIÓN
•AOI: Implementa una función lógica en el
orden AND, OR, NOT (Invert).
F = ( aib + cid )
SOP invertida (negada)
•OAI: Implementa una función lógica en el
orden OR, AND, NOT (Invert)
G = ( ( x + y )i( z + w ) )
POS invertida (negada)
17

18. DISEÑO DE CIRCUITOS LÓGICOS COMBINACIONALES
• Requerimiento
18

19. DISEÑO DE CIRCUITOS LÓGICOS COMBINACIONALES
• Requerimiento
• Se elabora la tabla de verdad.
19

20. DISEÑO DE CIRCUITOS LÓGICOS COMBINACIONALES
• Requerimiento
• Se elabora la tabla de verdad.
• Aplicar SOP ó POS.
20

21. DISEÑO DE CIRCUITOS LÓGICOS COMBINACIONALES
• Requerimiento
• Se elabora la tabla de verdad.
• Aplicar SOP ó POS.
• Simplificación de la función a su mínima
expresión.
21

22. PROCEDIMIENTO DE DISEÑO
Requerimiento
Diseñe un circuito lógico que tenga como entradas
A, B y C y cuya salida sea alta solo cuando la
mayor parte de las entradas sean ALTAS.
22

23. PROCEDIMIENTO DE DISEÑO (2)
A B C F Tabla de
0 0 0 0 Verdad
0 0 1 0
0 1 0 0
0 1 1 1
1 0 0 0
1 0 1 1
1 1 0 1
1 1 1 1
23

24. PROCEDIMIENTO DE DISEÑO (3)
Simplificación
Se escriben los términos, para los casos en que la
salida es “UNO” y se procede a simplificar
X = ABC + ABC + ABC + ABC
X = ABC + ABC + ABC + ABC + ABC + ABC
F = (ABC + ABC ) + (ABC + ABC ) + (ABC + ABC )
F = BC(A + A) + AC(B + B) + AB(C +C )
F = BC + AC + AB
24

25. PROCEDIMIENTO DE DISEÑO (4)
Implementación
25

26. EJEMPLO DE DISEÑO
# A B C D Z
0 0 0 0 0 1
• Halle una Función Z 1 0 0 0 1 0
que identifique 2 0 0 1 0 1
3 0 0 1 1 0
todos los números 4 0 1 0 0 1
pares del 0 al 15 5
6
0
0
1
1
0
1
1
0
0
1
7 0 1 1 1 0
8 1 0 0 0 1
9 1 0 0 1 0
10 1 0 1 0 1
11 1 0 1 1 0
12 1 1 0 0 1
13 1 1 0 1 0
14 1 1 1 0 1
15 1 1 1 1 0
26

27. EJEMPLO DE DISEÑO (2)
Z = ABC D + ABC D + ABC D + ABC D + ABC D + ABC D + ABC D + ABC D
• El algebra de Boole permite obtener expresiones
mas simples:
Z=D
• También el sentido común: En la tabla de verdad
anterior, un número par se identifica cuando el
bit menos significativo es 0.
27

28. APLICACIÓN
Diseño de alarma
Entradas:
P-> Puerta , V->Ventana, N->Noche, I-> interruptor
Salidas:
A-> Alarma
La salida (A) se activa si el interruptor está activado y la
puerta esta abierta o si es de noche y la ventana esta
abierta.
28

29. SOLUCIÓN
29

30. SOLUCIÓN
30