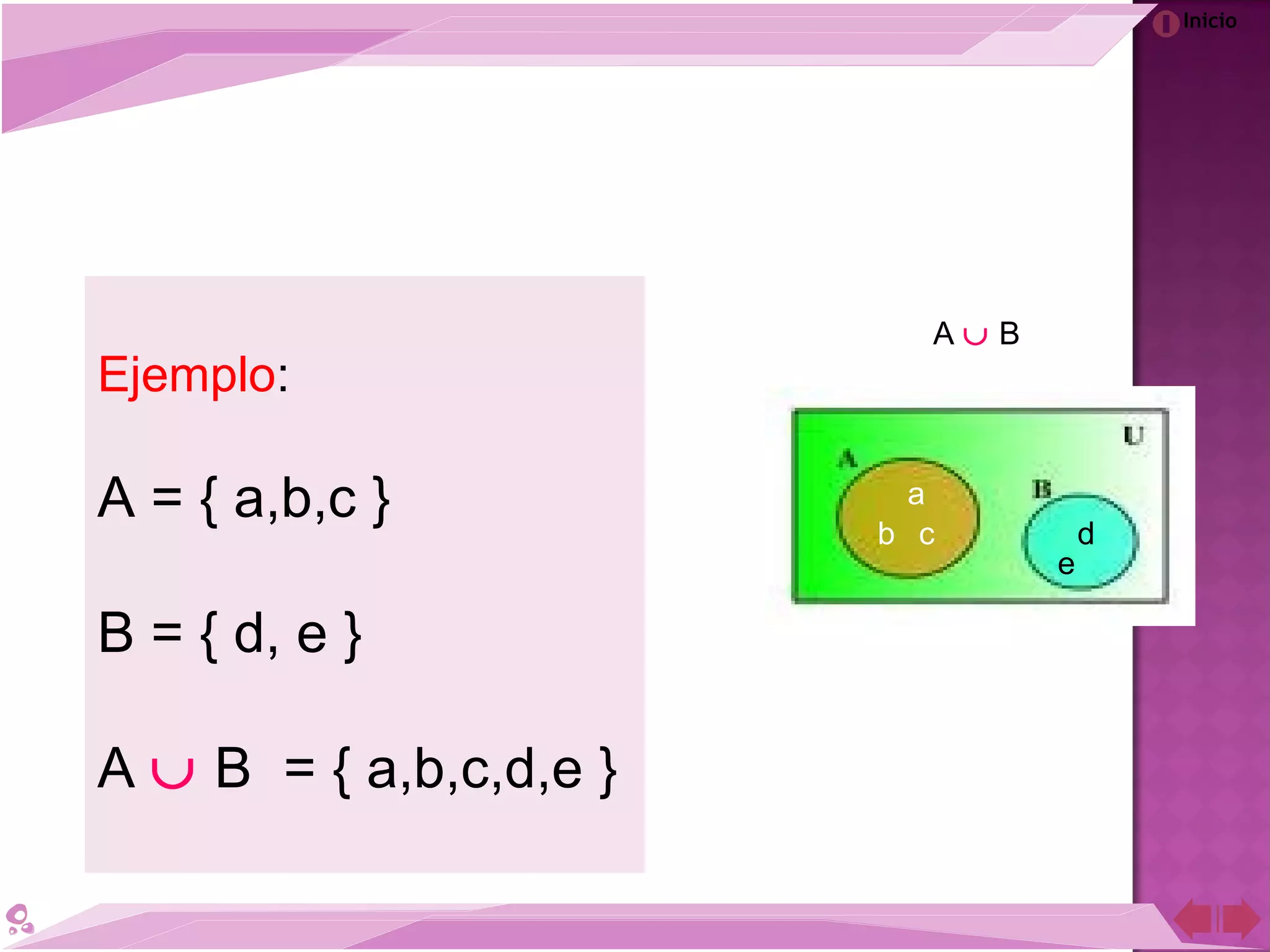
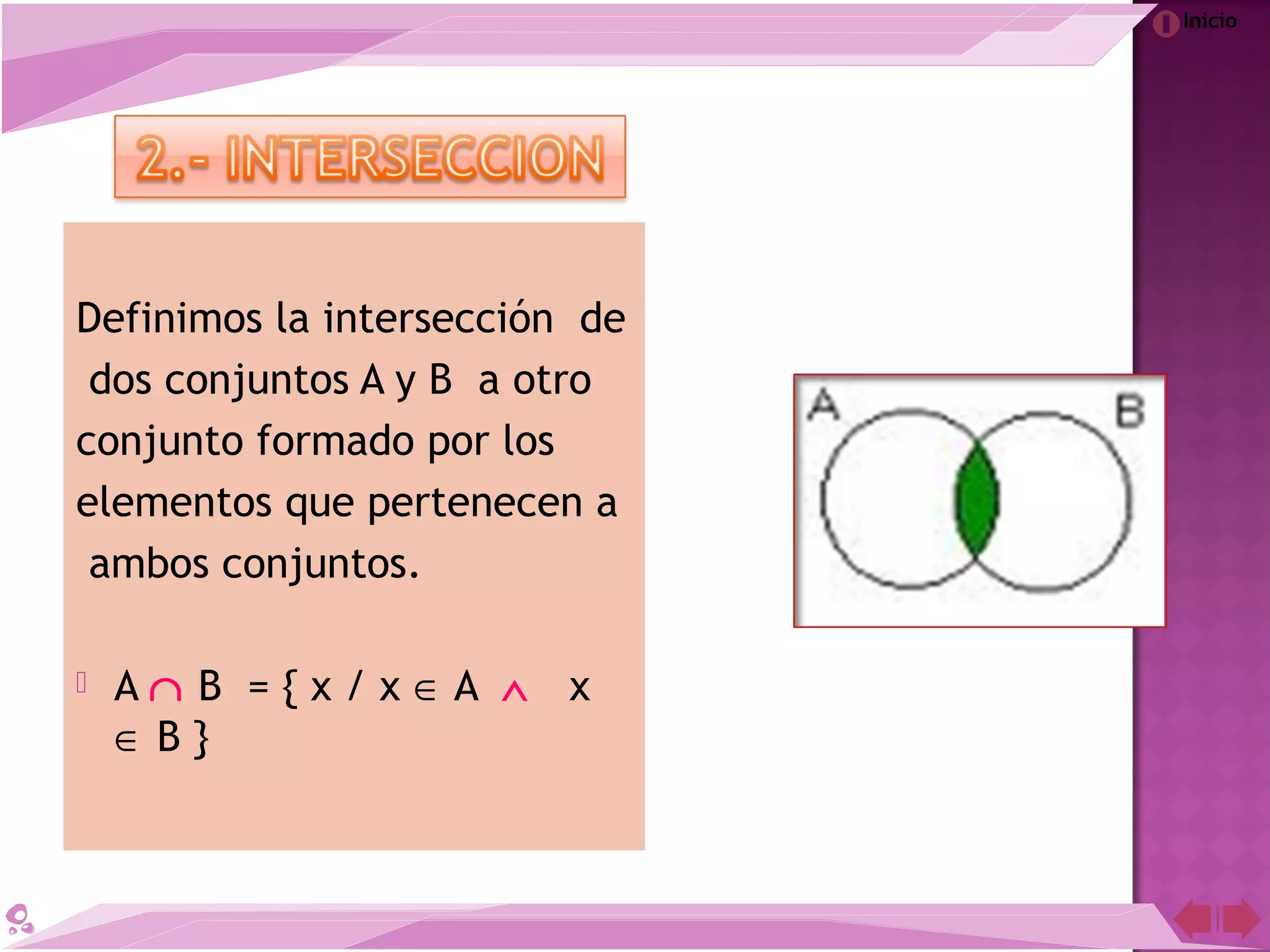
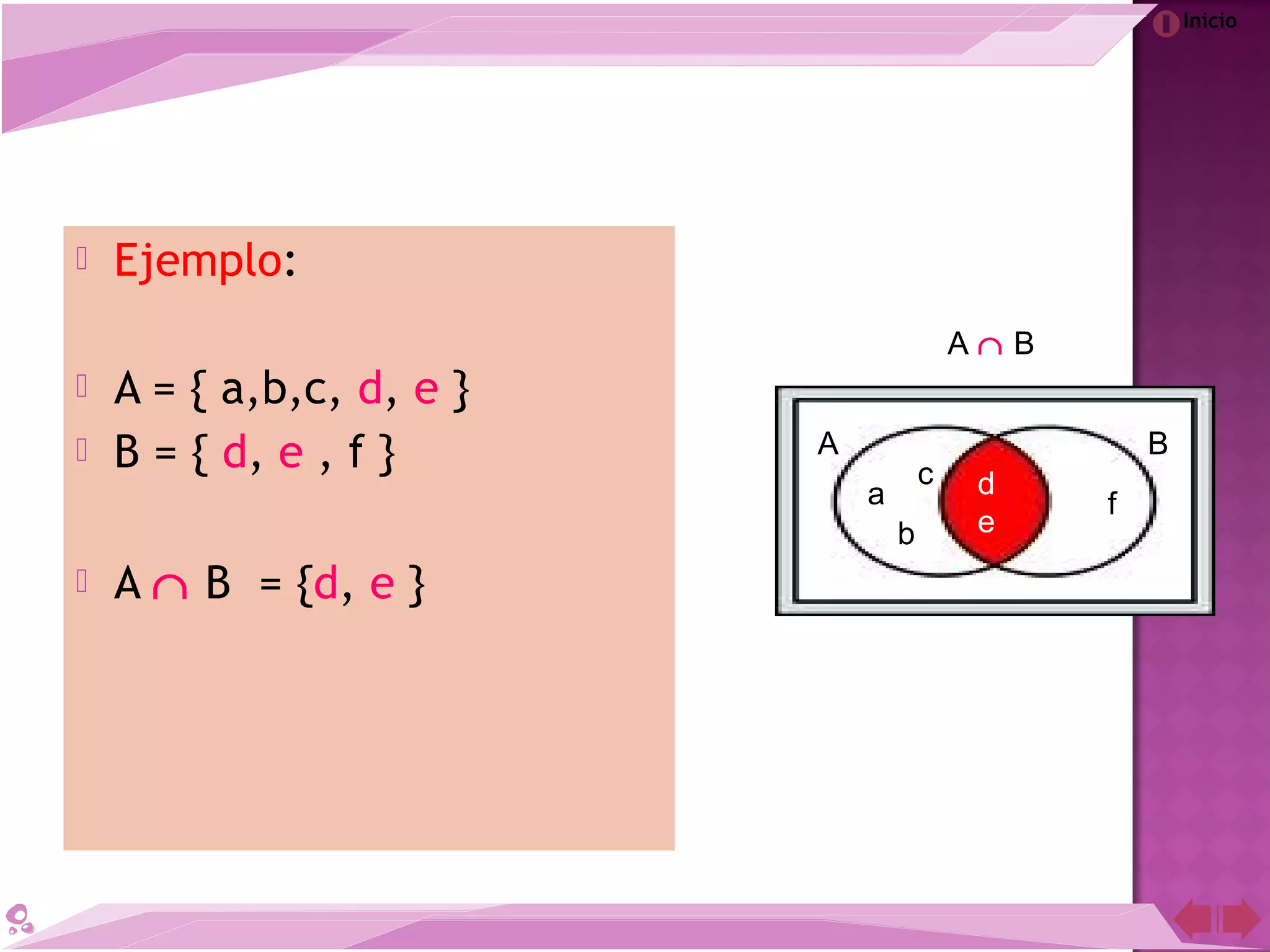
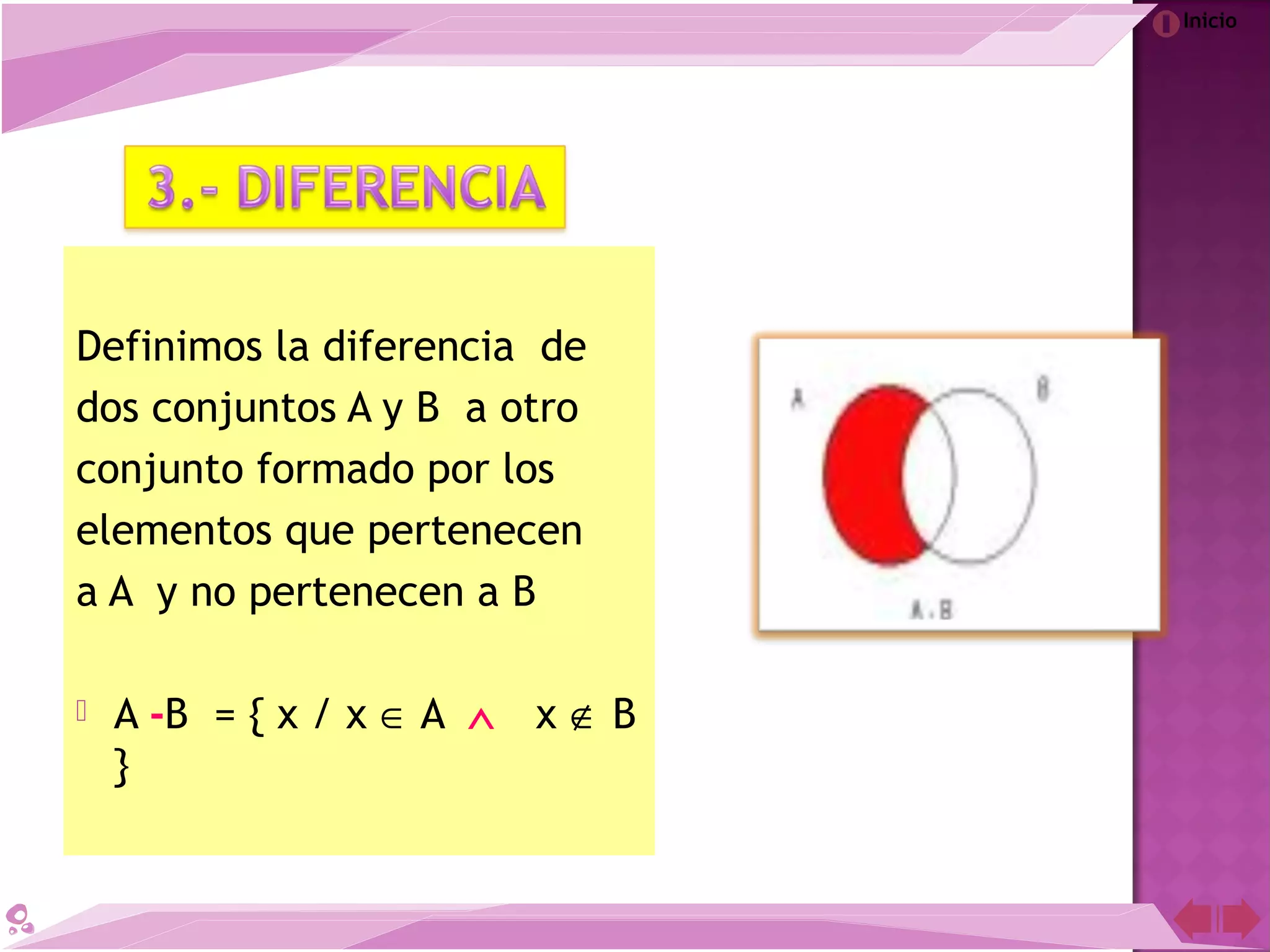
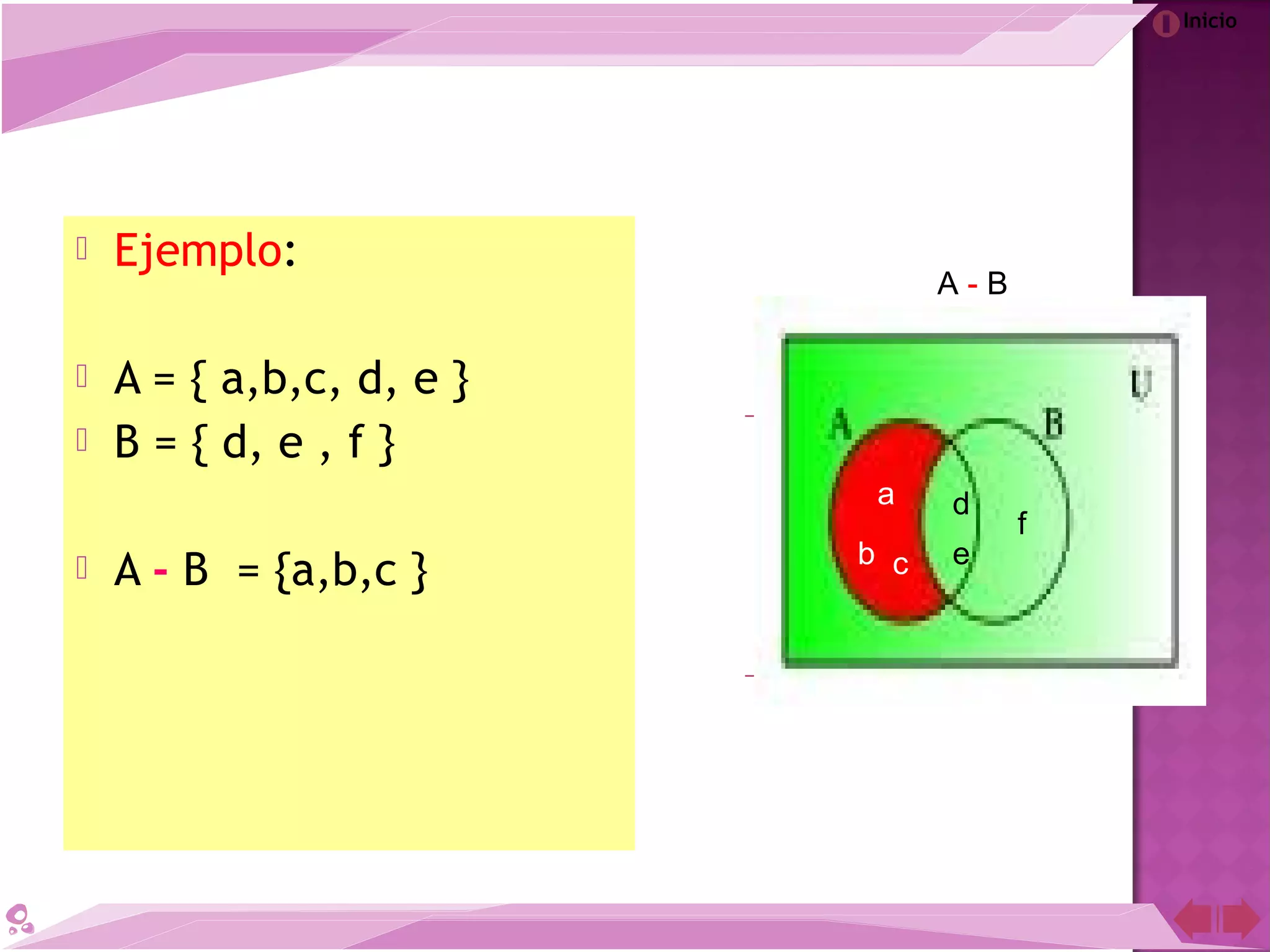
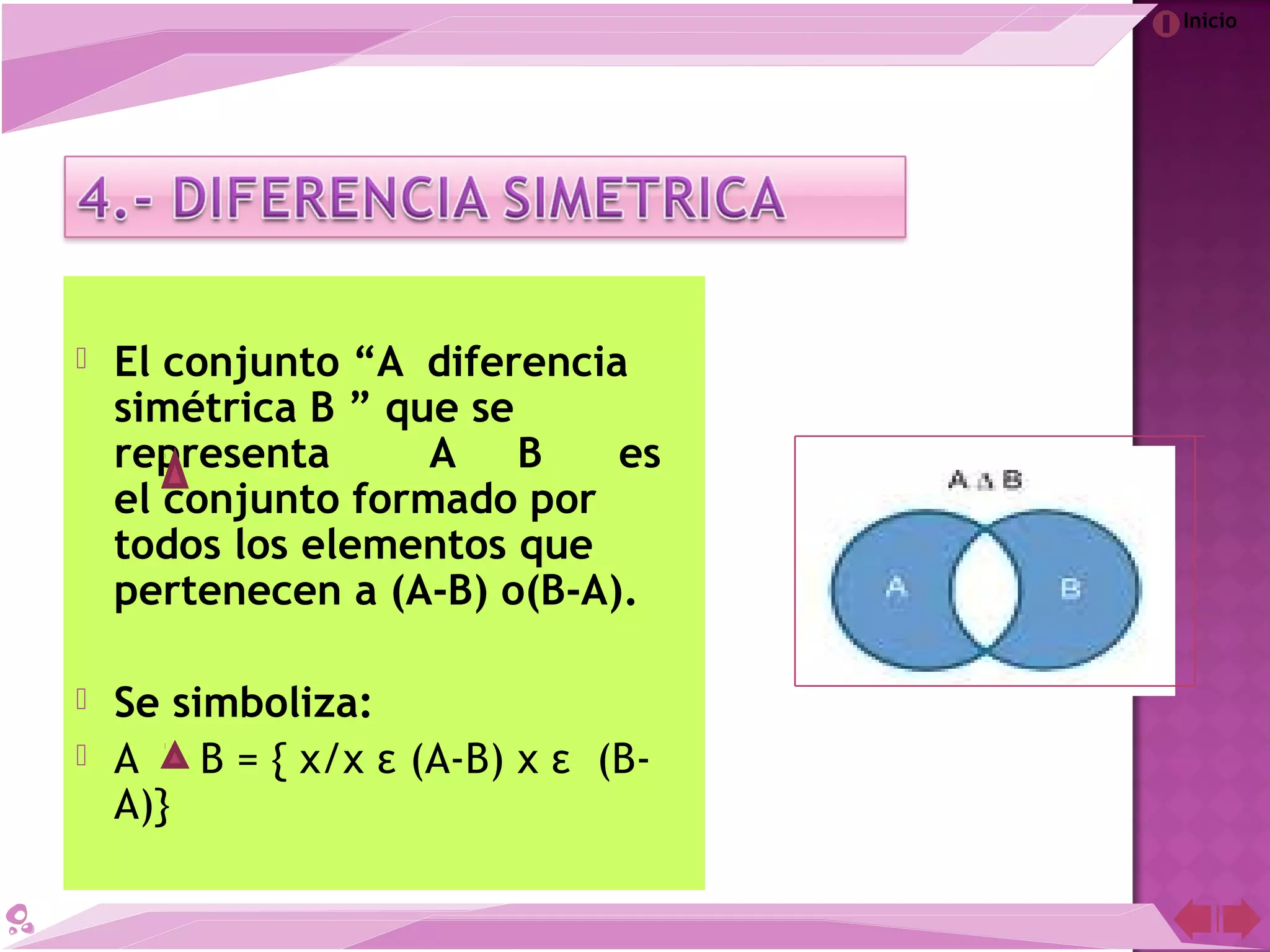
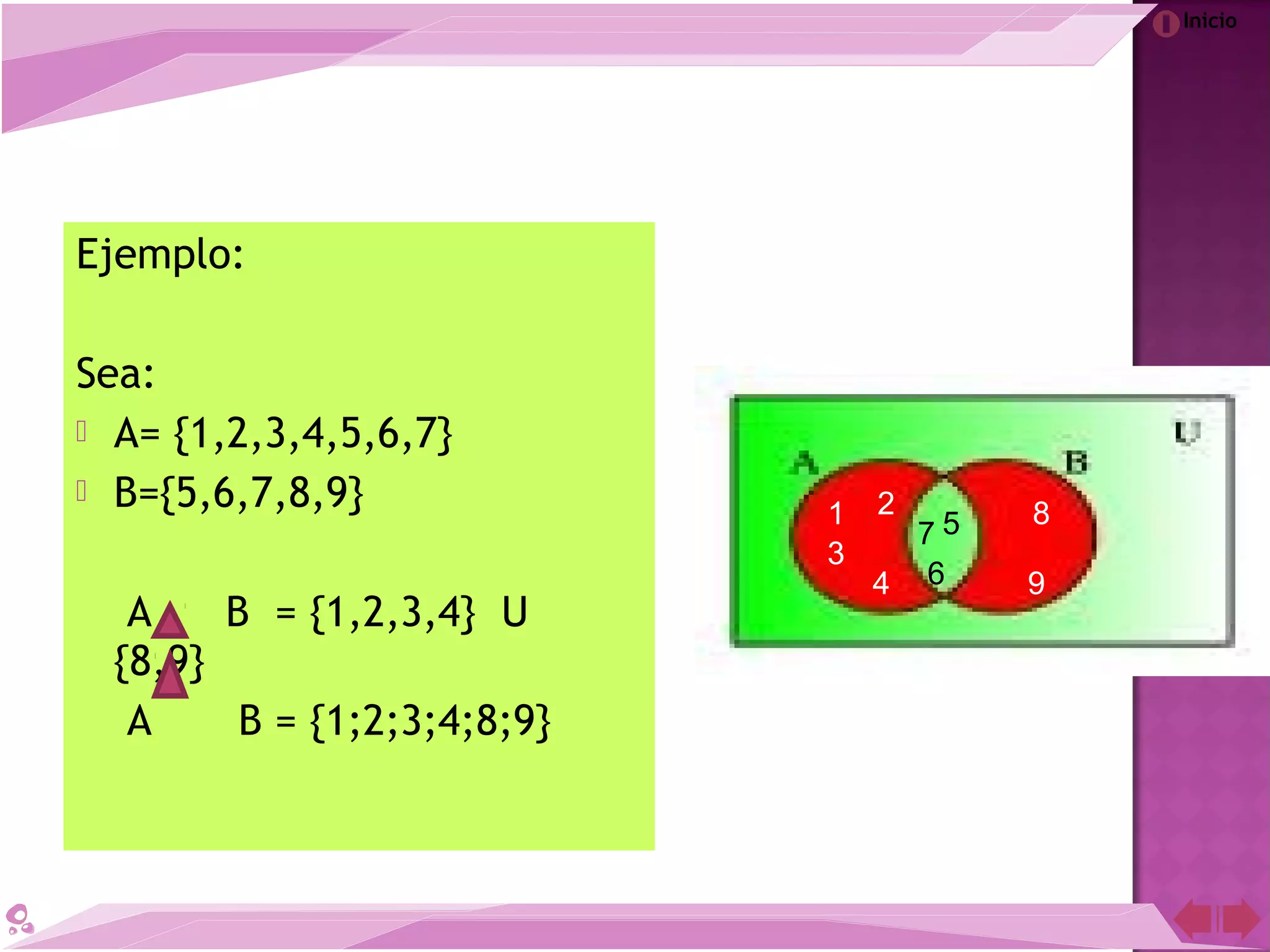
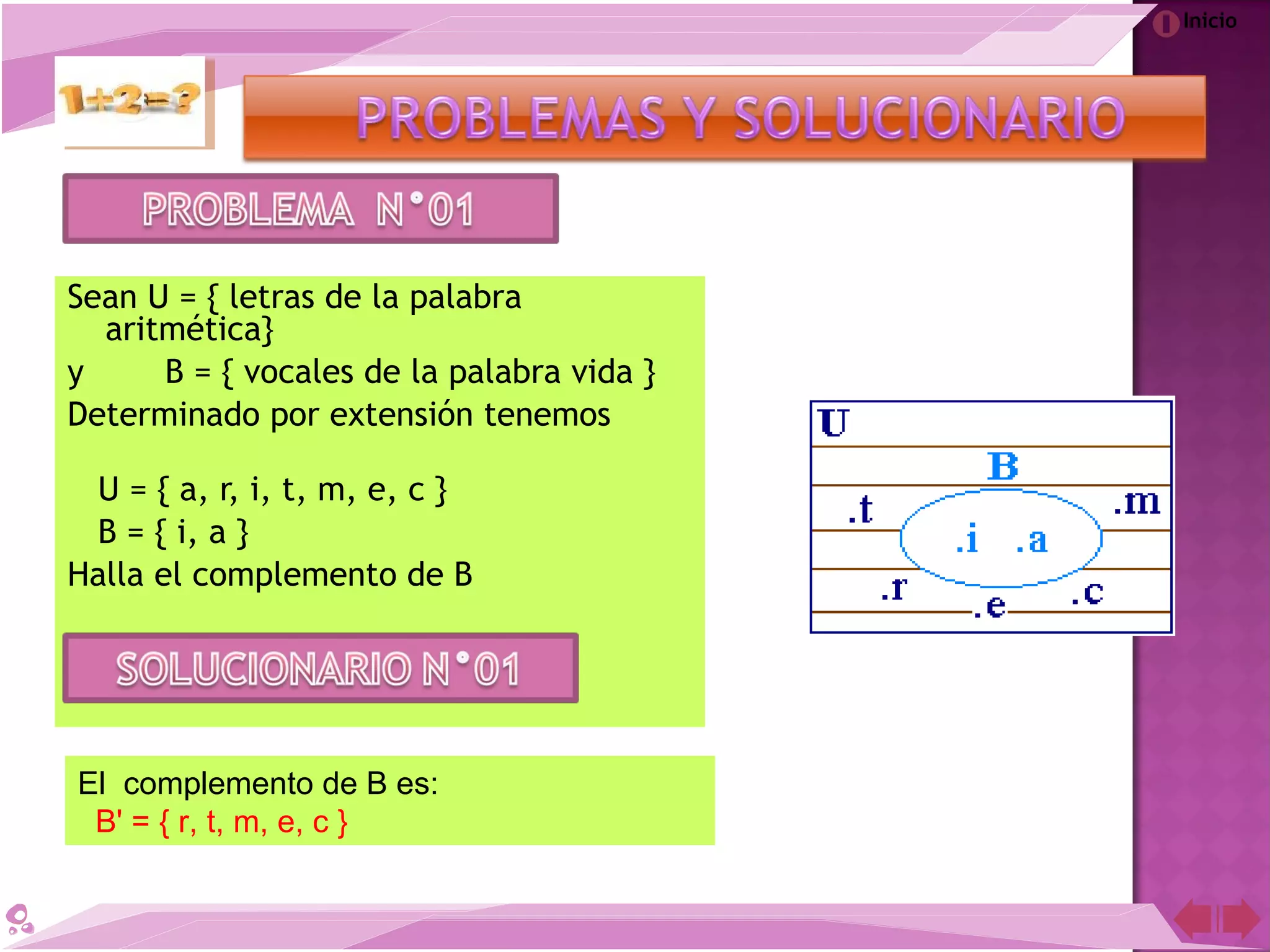
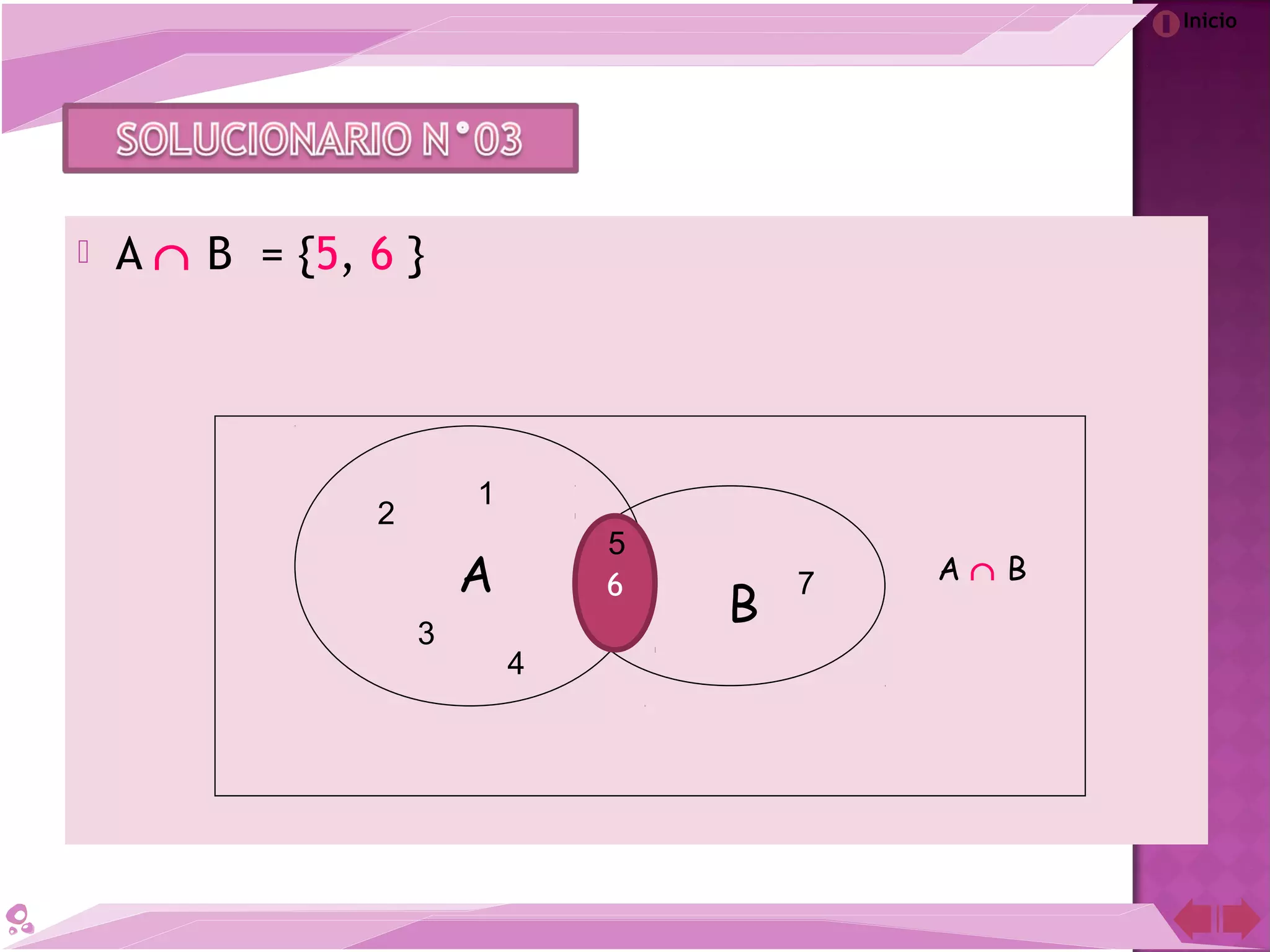
El documento describe la teoría de conjuntos desarrollada por el matemático Georg Cantor a finales del siglo XIX. Cantor definió los conjuntos como colecciones de objetos reales o abstractos y demostró que para cada conjunto infinito existe otro de mayor cardinalidad. A pesar de la controversia que generó en su época, la teoría de conjuntos de Cantor es ahora una de las teorías más importantes en la historia de las matemáticas.