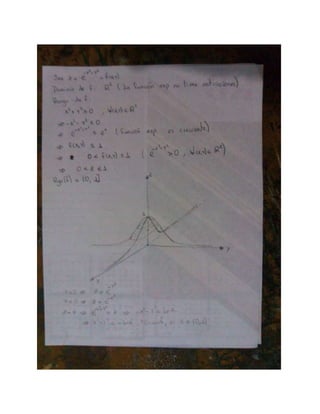
1. Demuestra que el límite no existe cuando x tiende a cero de la función y = x/x. 2. Dibuja la gráfica de la función y = e^x - x^2 y determina su dominio y rango. 3. Muestra que la ecuación diferencial satisface la ecuación u^2 = x^2 + y^2.

1. UNIVERSIDAD FERMIN TORO
CABUDARE.ESTADO LARA
Apellidos Nombres
Cédula Fecha
Asignación práctica N°1
1. Demuestre que el limite no existe 22
22
)0,0(),(
lim
yx
yx
yx 


2. Dibuje la grafica de la función
22
),( yx
eyxf 
 .Determine el dominio y rango
3. Dada
22
)()(
1
ln),(
byax
yxu

 satisface la ecuación 02
2
2
2






y
u
x
u
4. Sea ),( yxfz  y que cosrx  y rseny  .Muestre que
2
2
222
1

































z
rr
z
y
z
x
z
5. Uno de los lados de un rectángulo, es a=10 cm, el otro b=24 cm.¿como variará la
diagonal “L” de este rectángulo si el lado a se alarga 4 mm y el lado b se acorta 1
mm?. Hallar la magnitud aproximada de la variación y compararla con la exacta.
Use diferenciall total
15