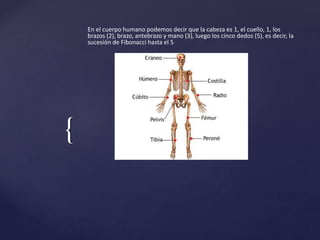
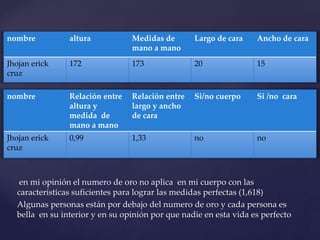
Leonardo Fibonacci fue un matemático italiano del siglo XIII que difundió en Occidente los conocimientos matemáticos del mundo árabe. Popularizó el uso de las cifras arábicas y expuso principios de trigonometría. La sucesión de Fibonacci se encuentra presente en el reino vegetal, animal y el cuerpo humano. El número áureo también está relacionado con la sucesión de Fibonacci y se puede encontrar en obras de arte y arquitectura.

1. Leonardo de pissa
{
(Leonardo Bigollo, llamado también Leonardo Fibonacci, Leonardo Pisano,
Leonardo Bonacci o Fibonacci; Pisa, actual Italia, c. 1175 - id., c. 1240)
Matemático italiano que difundió en Occidente los conocimientos científicos del
mundo árabe, los cuales recopiló en el Liber Abaci (Libro del ábaco). Popularizó
el uso de las cifras árabes y expuso los principios de la trigonometría en su obra
Practica Geometriae (Práctica de la geometría).
Fibonacci
Considerado como el primer algebrista de Europa (cronológicamente hablando)
y como el introductor del sistema numérico árabe, fue educado de niño en
Argelia, donde su padre era funcionario de aduanas, y donde aprendió "el
ábaco, al uso de los indios". Después tuvo manera, por razones de tipo
comercial, de conocer todo lo que de esta ciencia se enseñaba en Egipto, en
Siria, en Sicilia y en Provenza. Al material así reunido le dio un orden, una unidad
de método y una claridad de enseñanza en el Liber Abaci (Libro del ábaco), que,
como modelo de texto universitario, sirvió también, por su caudal de ejemplos,
para la compilación de manuales de aritmética para uso de los comerciantes.

2. {
2. Presencia de la sucesión de Fibonacci en el reino vegetal,
reino animal y el cuerpo humano
*Pero los números de la sucesión de Fibonacci van a
sorprender a todos los biólogos.
Como muy bien nos enseña la filotaxia, las ramas y las
hojas de las plantas se distribuyen buscando siempre
recibir el máximo de luz para cada una de ellas. Por eso
ninguna hoja nace justo en la vertical de la anterior. La
distribución de las hojas alrededor del tallo de las
plantas se produce siguiendo secuencias basadas
exclusivamente en estos números.
El número de espirales en numerosas flores y frutos
también se ajusta a parejas consecutivas de términos
de esta sucesión: los girasoles tienen 55 espirales en
un sentido y 89 en el otro, o bien 89 y 144.

3. {
Una pareja de conejos tarda un mes en alcanzar la edad fértil, a partir
de ese momento cada vez engendra una pareja de conejos, que a su
vez, tras ser fértiles engendrarán cada mes una pareja de conejos.
¿Cuántos conejos habrá al cabo de un determinado número de meses?
En este gráfico vemos que el número de parejas a lo largo de
los meses coincide con los términos de la sucesión.
Veamos con detalle estos números. 1; 1; 2; 3, 5; 8; 13; 21; 34;
55; 89, 144....

4. {
En el cuerpo humano podemos decir que la cabeza es 1, el cuello, 1, los
brazos (2), brazo, antebrazo y mano (3), luego los cinco dedos (5), es decir, la
sucesión de Fibonacci hasta el 5

5. {
En el panteón cumple con lo plateado por el
numero de oro y es agradable a la vista

6. {
En esta imagen podemos ver perfectamente en el triangulo
aureo y en el rectángulo agureo la perfección de la obra

7. {
en esta imagen podemos ver claramente la espirar que se
forma y por lo tanto cumple con lo de fibonassi

8. {
en esta imagen podemos ver según es tema tratado la figura del
numero aureo en la etapa de crecimiento de un feto y en las
galaxias (podemos decir que casi todo cumple con esta regla del
numero aureo)

9. Numero de oro
{

10. {
El número áureo es la relación o proporción que guardan entre sí dos segmentos de
rectas. Fue descubierto en la antigüedad, y puede encontrarse no solo en figuras
geométricas, sino también en la naturaleza. A menudo se le atribuye un carácter estético
especial a los objetos que contienen este número, y es posible encontrar esta relación en
diversas obras de la arquitectura u el arte
El descubrimiento de este número se atribuye a la escuela Pitagórica, de hecho los
pitagóricos utilizaban como símbolo la estrella de cinco puntas, en la que aparecen
distintas razones áureas.
Es fácil encontrar distintas proporciones áureas en diversas figuras. Este número aparece
repetidamente en el mundo que nos rodea, como elemento de diseño en construcciones
arquitectónicas tan antiguas como la pirámide de Keops, o en distintos seres vivos, tanto
en el reino vegetal (flores, semillas,...) como en el reino animal (estrellas de mar,
caracolas que crecen en función de relaciones áureas,...) Leonardo da Vinci en su
"Esquema de las proporciones del cuerpo humano" señala distintas relaciones áureas
que existen en el ser humano.
FI (j) Este número recibe su nombre del escultor Fidias (siglo V adC, autor del friso y del
frontis del Partenón), quien utilizó ampliamente sus propiedades en su destacada obra
artística.

11. {
*Relación Con el número de oro
El número áureo también está "emparentado" con la serie de
Fibonacci. Si llamamos Fn al enésimo número de Fibonacci y Fn+1 al
siguiente, podemos ver que a medida que n se hace más grande, la
razón entre Fn+1 y Fn oscila, siendo alternativamente menor y
mayor que la razón áurea.
Si vamos dividiendo cada valor de la Serie de Fibonacci por el
anterior, el resultado tiende a Phi. Cuanto más altos son los valores,
mayor es la aproximación (considerad que Phi, como todo número
irracional, tiene infinitos decimales).

12. {
Ejemplos de rectángulos áureos los podemos
encontrar en las tarjetas de crédito, en nuestro
carnet de identidad y también en las cajetillas
de tabaco.

13. nombre altura Medidas de
172 173 20 15
nombre Relación entre
altura y
medida de
mano a mano
{
mano a mano
Largo de cara Ancho de cara
Jhojan erick
cruz
Relación entre
largo y ancho
de cara
Si/no cuerpo Si /no cara
Jhojan erick
cruz
0,99 1,33 no no
en mi opinión el numero de oro no aplica en mi cuerpo con las
características suficientes para lograr las medidas perfectas (1,618)
Algunas personas están por debajo del numero de oro y cada persona es
bella en su interior y en su opinión por que nadie en esta vida es perfecto

14. { gracias