Este documento presenta varios ejemplos de cómo generar y analizar datos aleatorios en R. Se muestran instrucciones para crear distribuciones normales y binomiales, y se analizan conjuntos de datos reales mediante histogramas, diagramas de caja y tablas. El documento también incluye ejemplos de cómo limpiar datos eliminando valores atípicos y crear diferentes tipos de gráficos para visualizar los datos, como diagramas de barras apiladas y no apiladas.

1. 1. R permite generar ciatos aleatorios con gran facilidad mediante
instrucciones específicas que empiezan con "r" (rnorm, rpois, rbinom, .
. .).
(a) Genera 100 valores de una distribución normal con rnorm(100).
(b) Realiza un histograma de los valores. Repite el proceso un par de veces.
¿Qué observas?
hist(normal,col=rainbow(5), ylim=c(0, 25), xlim=c(-3,3))

2. Se observa que el grafico es simétrico respecto a 0, alrededor de 0 se presenta
la mayor frecuencia.
(c) Realiza un resumen numérico de los datos.
> summary(normal)
Min. 1st Qu. Median Mean 3rd Qu. Max.
-2.42500 -0.63250 0.02284 0.05490 0.75270 2.11100
> summary(normal1)
Min. 1st Qu. Median Mean 3rd Qu. Max.
-2.1710 -0.8972 -0.1605 -0.0558 0.7208 2.5020
> summary(normal2)
Min. 1st Qu. Median Mean 3rd Qu. Max.
-3.04600 -0.73190 -0.07056 -0.07266 0.64730 2.58100
> summary(normal3)
Min. 1st Qu. Median Mean 3rd Qu. Max.
-2.59900 -0.83440 -0.15680 -0.09642 0.55590 2.61700
2. De forma similar al ejercicio genera 30 valores de una distribución
binomial de parámetros
(n=5 y p=2/3).
(a) Representa los resultados con un diagrama de barras o de pastel.

4. (b) Realiza un resumen numérico de los datos y compáralo con el del ejercicio
anterior.
summary(Binomial)
Min. 1st Qu. Median Mean 3rd Qu. Max.
1.000 3.000 3.000 3.167 4.000 5.000
¿Qué deberías hacer para obtener un resumen similar?
> fivenum(Binomial)
[1] 1 3 3 4 5
3. El conjunto de datos brightness contiene información sobre el brillo de
966 estrellas.
(a) Representa estos datos mediante un histograma

5. (b) Representa gráficamente estos datos mediante un diagrama de caja
(boxplot). ¿Dirías que los datos presentan "outliers"? Cuál es el segundo menor
outlier?

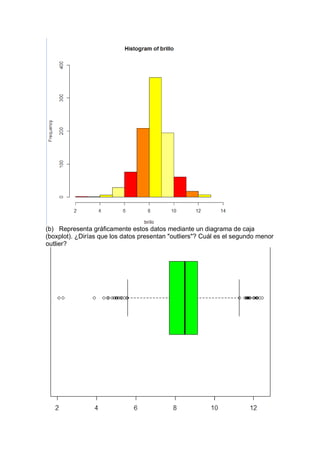
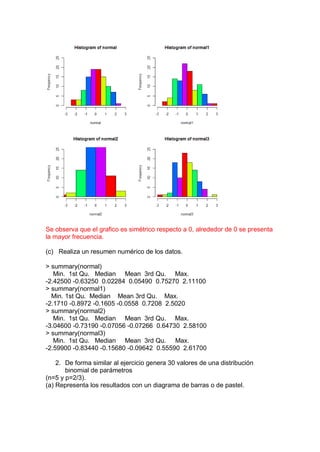
6. Si, claramente se observan muchos outliers.
Aplicando boxplot.stats(brillo), encontramos que el segundo menor outlier es
5.54
(c) Deseamos conservar los datos que de ninguna forma puedan ser
considerados atípicos. Crea una nueva variable denominada brightness.sin que
contenga tan sólo los valores que se encuentren por encima de la primera
bisagra y por debajo de la cuarta.
En este caso debemos conservar los valores por encima de 5.57 y por debajo
de 11.26. Lo cual se puede lograr mediante los siguientes comandos:
brillo.sin<-brillo[brillo<=11.26]
brillo.sin<-brillo.sin[brillo.sin>=5.57]
4. En una encuesta en la que se evalúa el funcionamiento de un curso se
han recogido las siguientes respuestas de 10 estudiantes a tres
preguntas P1, P2 y P3:
(a) Entra los datos mediante c() scan() , read.table() o read.csv().
(b) Tabula los resultados de cada pregunta por separado.
> table(p1)
p1
34
64
> table(p2)
p2
245
415

7. > table(p3)
p3
13
82
(c) Realiza tablas de contingencia cruzadas para cada pregunta, de 2 en 2 y
las 3 a la vez.
(d) Haz un diagrama de barras apiladas de las preguntas 2 y 3.

8. (e) Haz un diagrama de barras con las tres preguntas simultáneamente.
5. El paquete MASS contiene la base de datos UScereal con información
relativa a desayunos con cereales.
(a) ¿Cual es el tipo de datos de cada variable?
Tipo numéricas:
"calories" "protein" "fat" "sodium" "fibre" "carbo" "sugars" "shelf"
"potassium"
Tipo factor:
"mfr" "vitamins"

9. (b) Utiliza los datos de cereales para investigar algunas asociaciones entre sus
variables:
i. La relación entre manufacturer y shelf.
Estadísticamente no existe relacione entre manufacturer y shelf.
ii. La relación entre fat y vitamins.
Estadísticamente no existe relacione entre fat y vitamins
iii. La relación entre fat y shelf.
Estadísticamente no existe relacione entre fat y shelf

10. ayuda