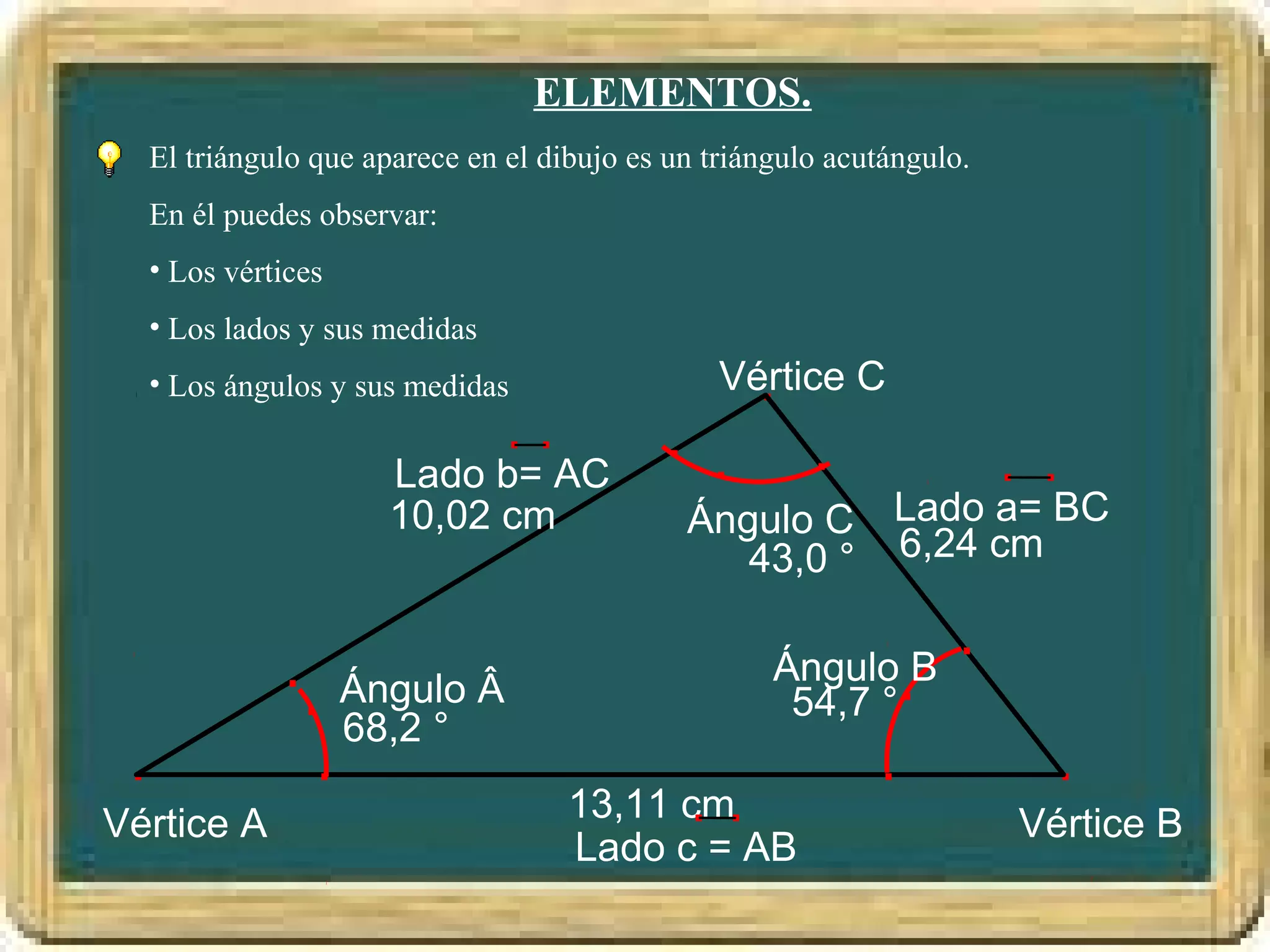
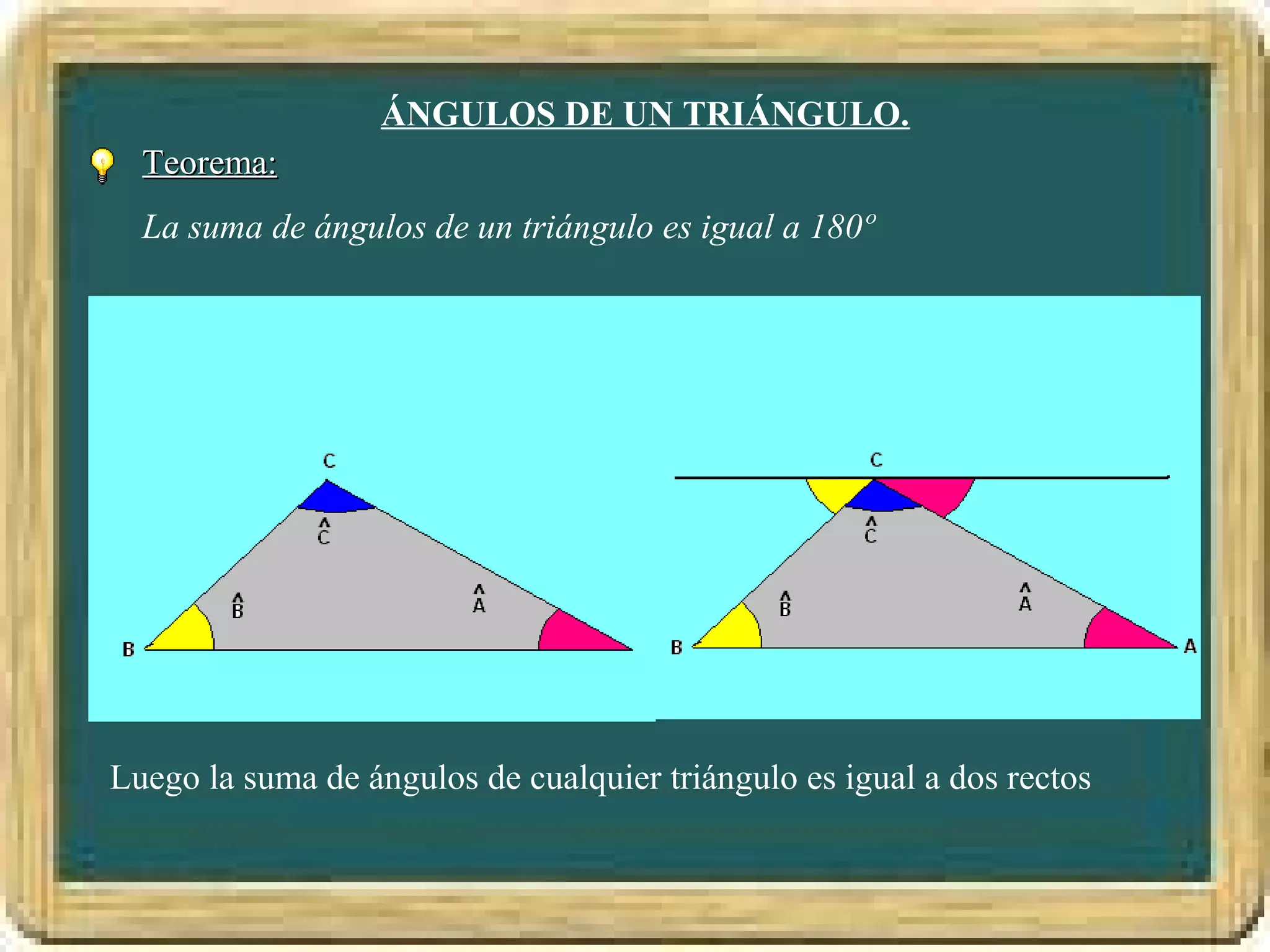
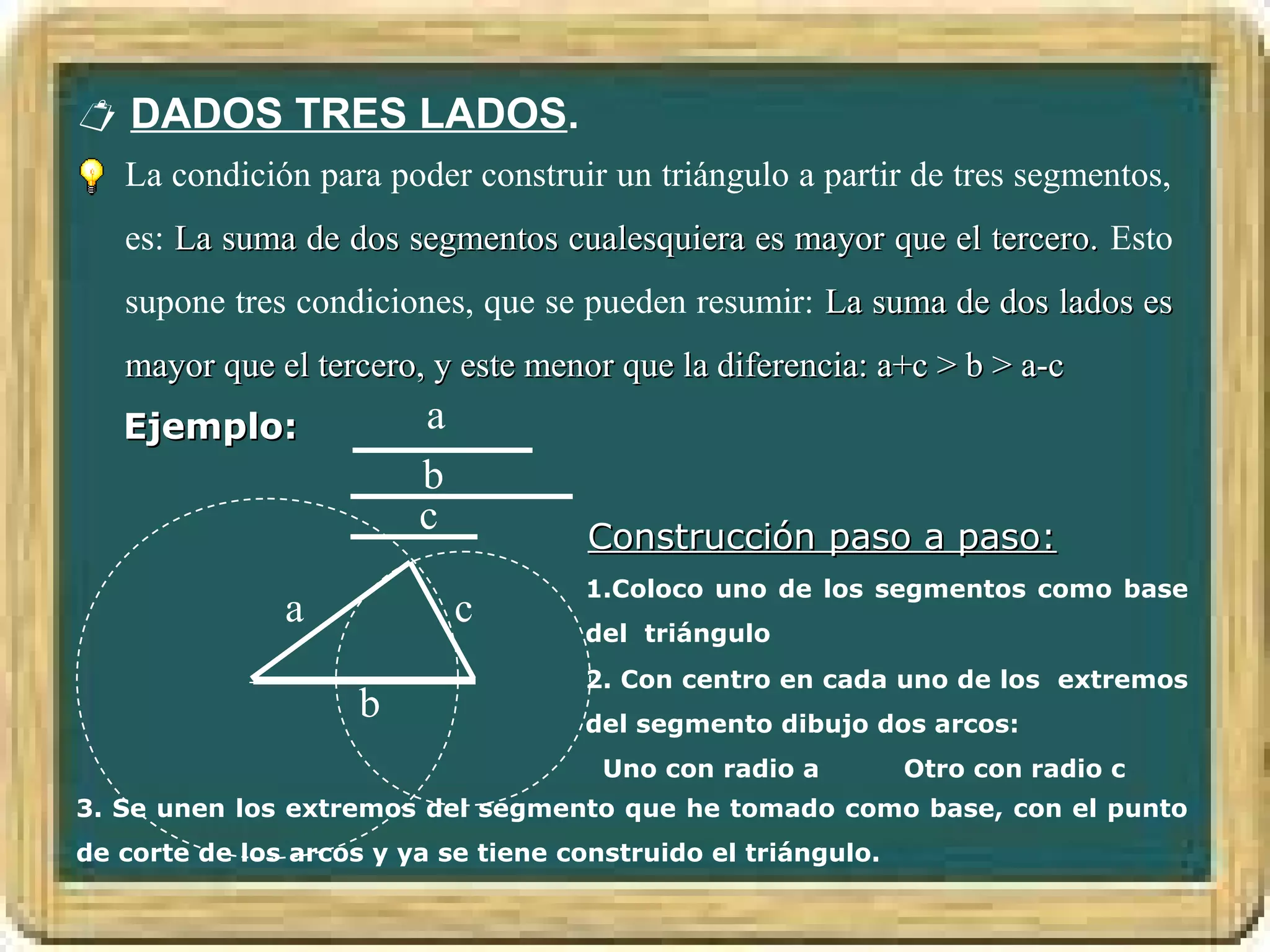
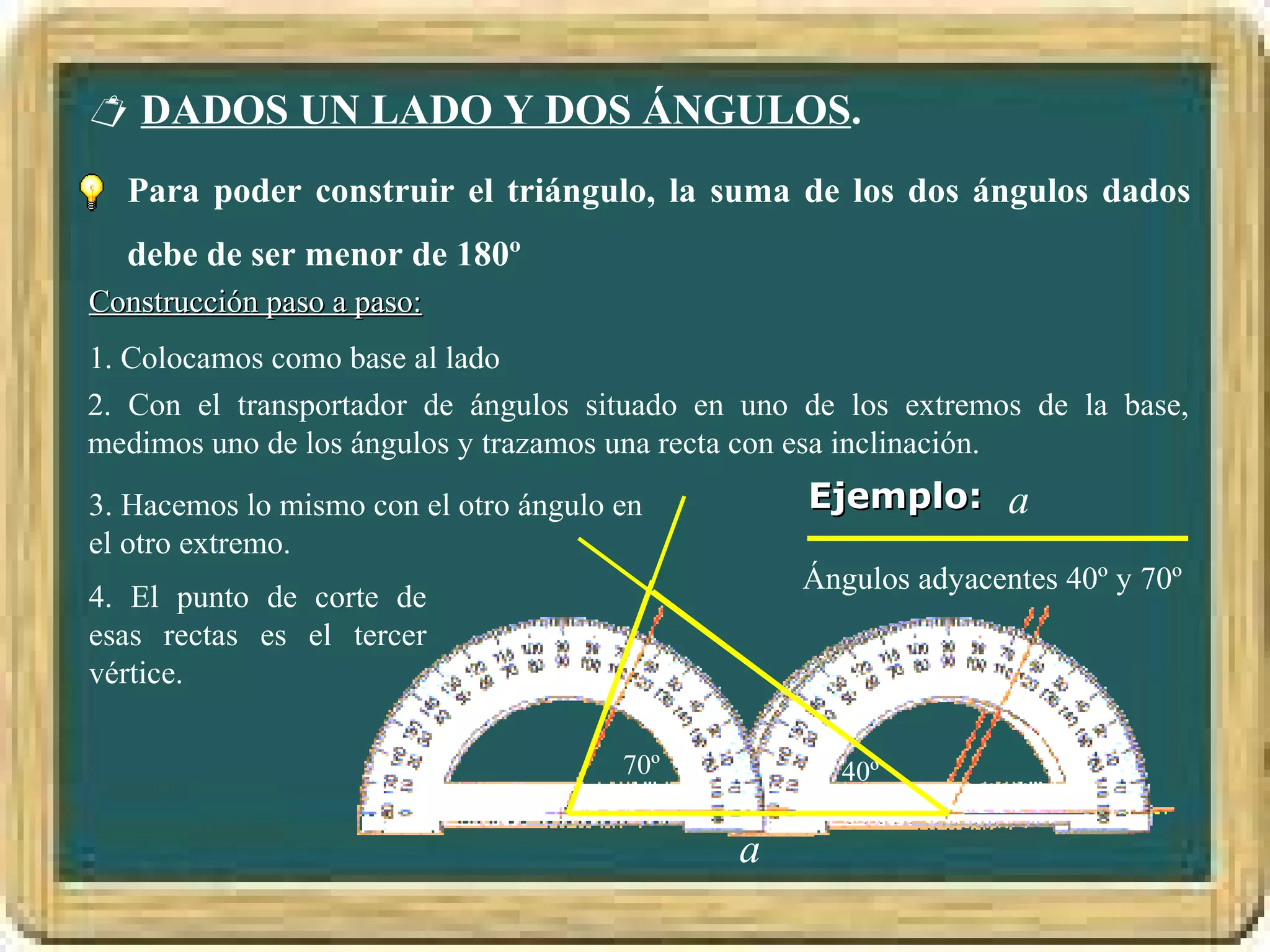
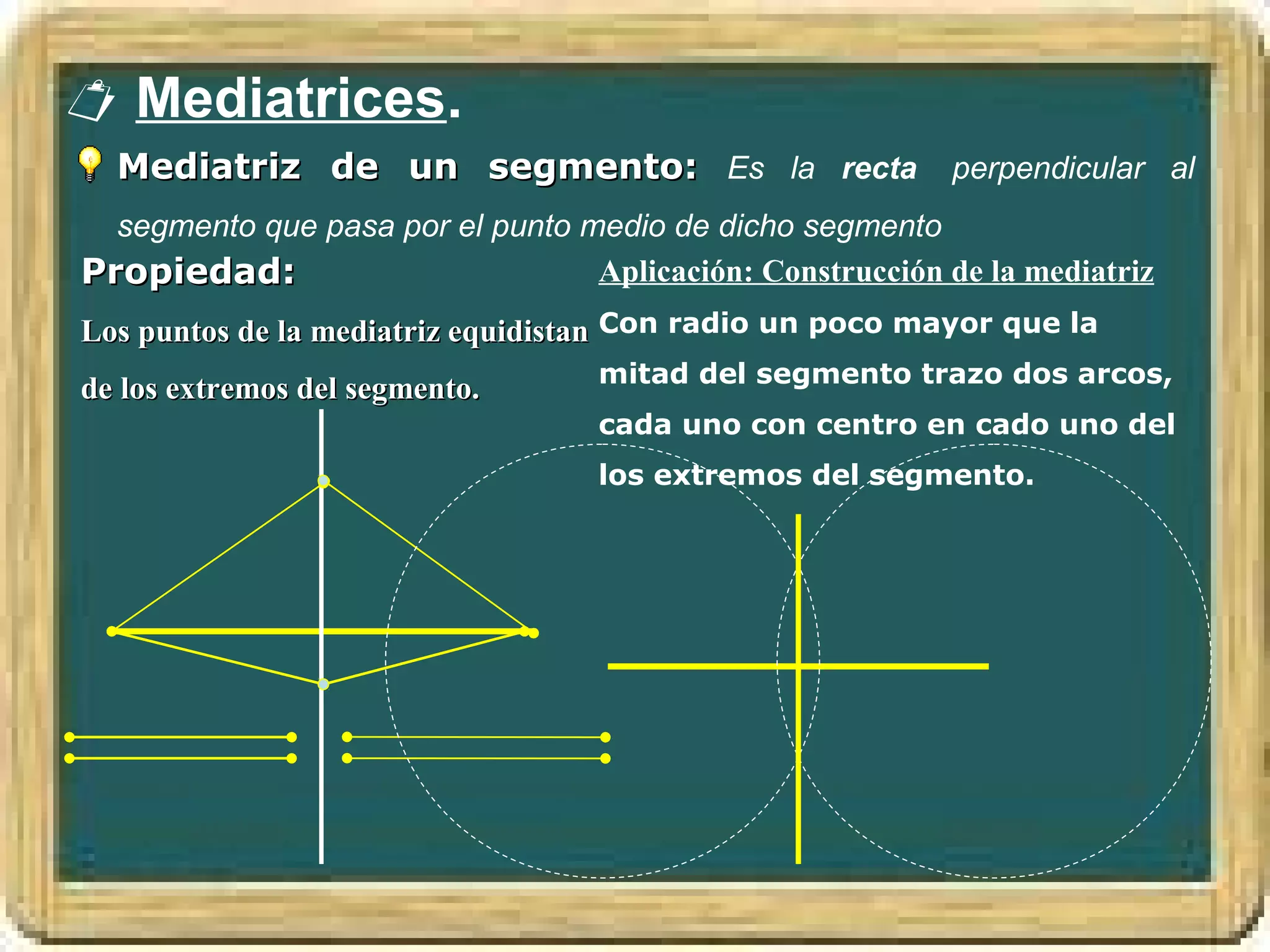
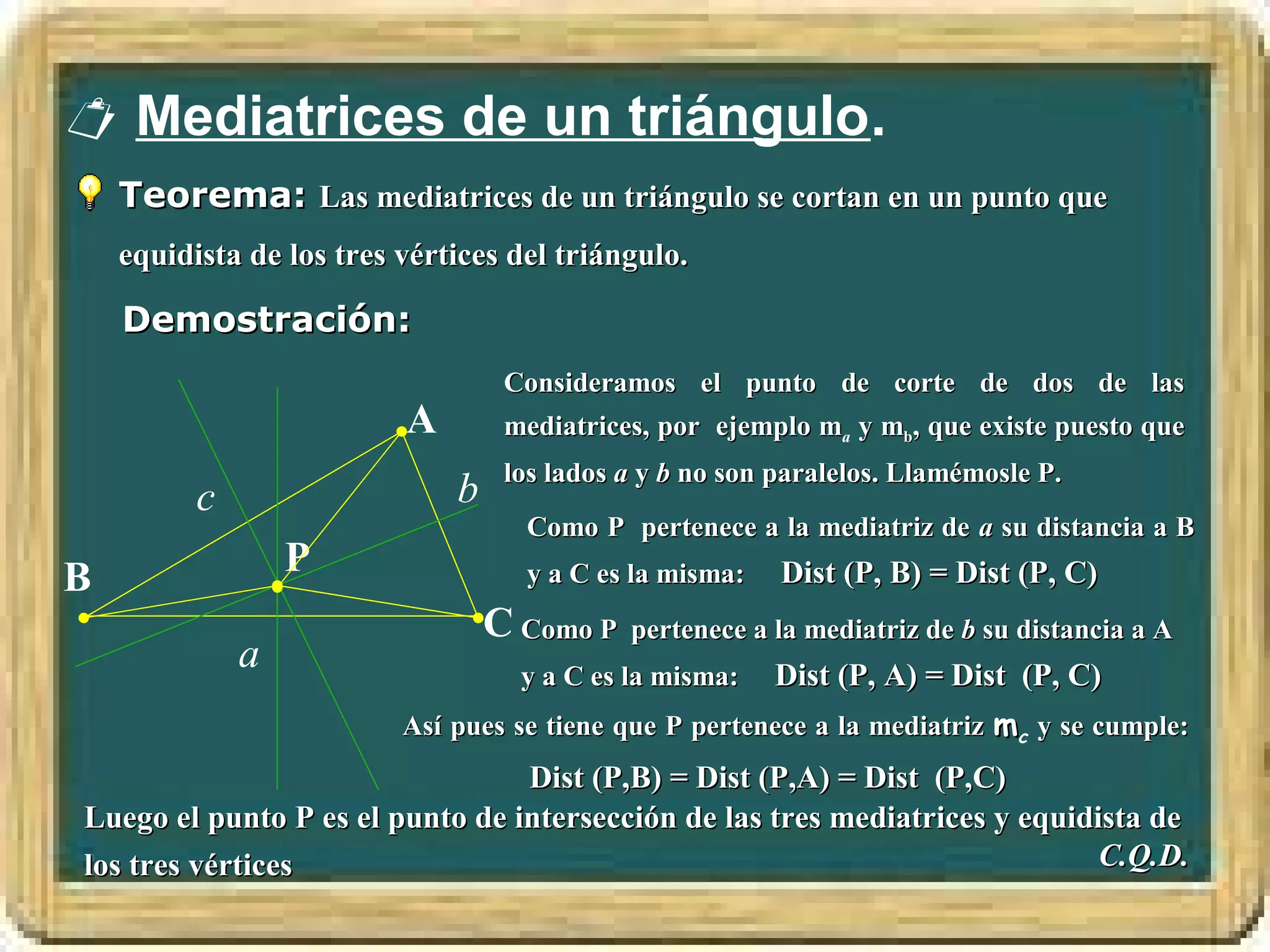
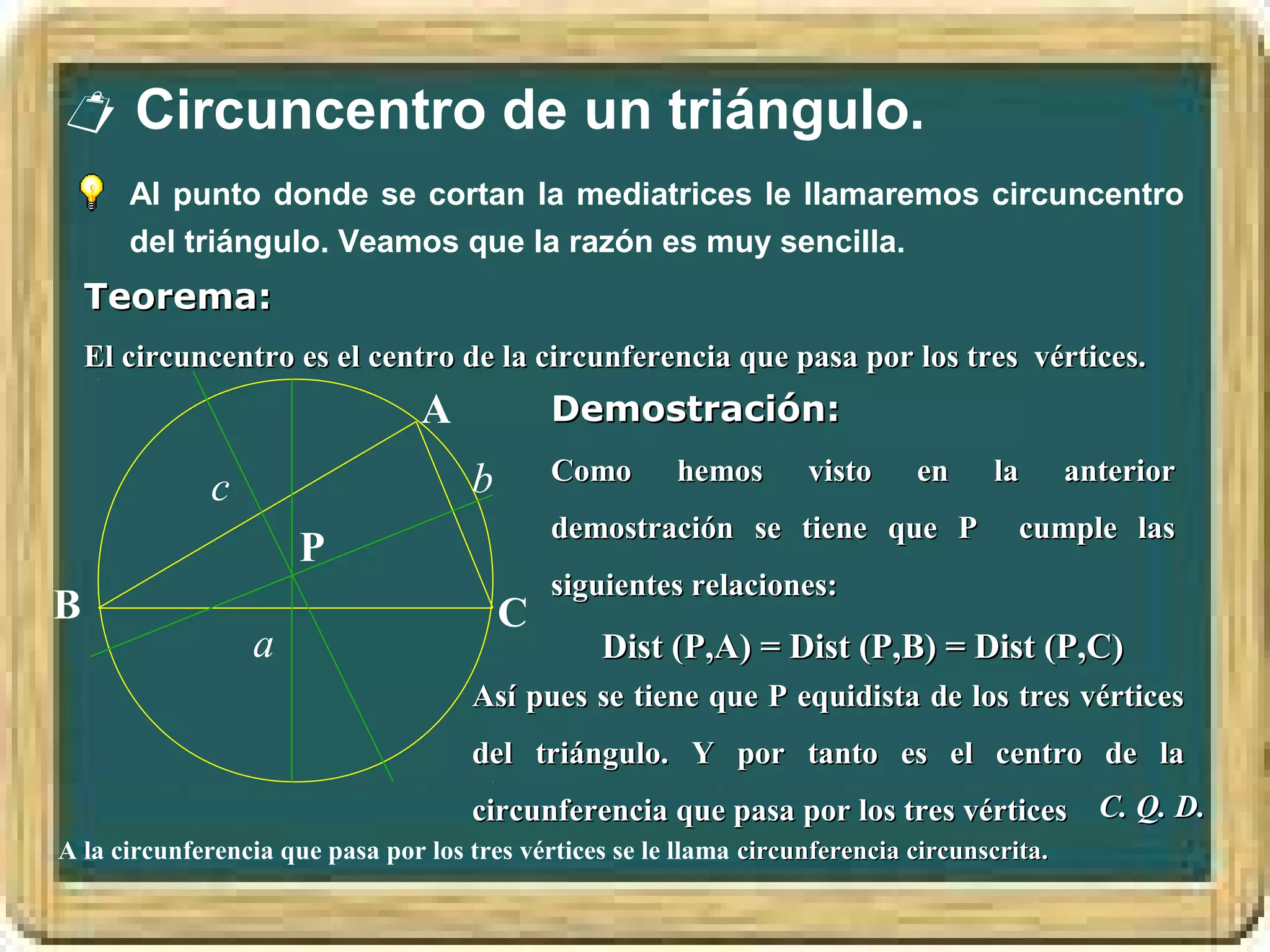
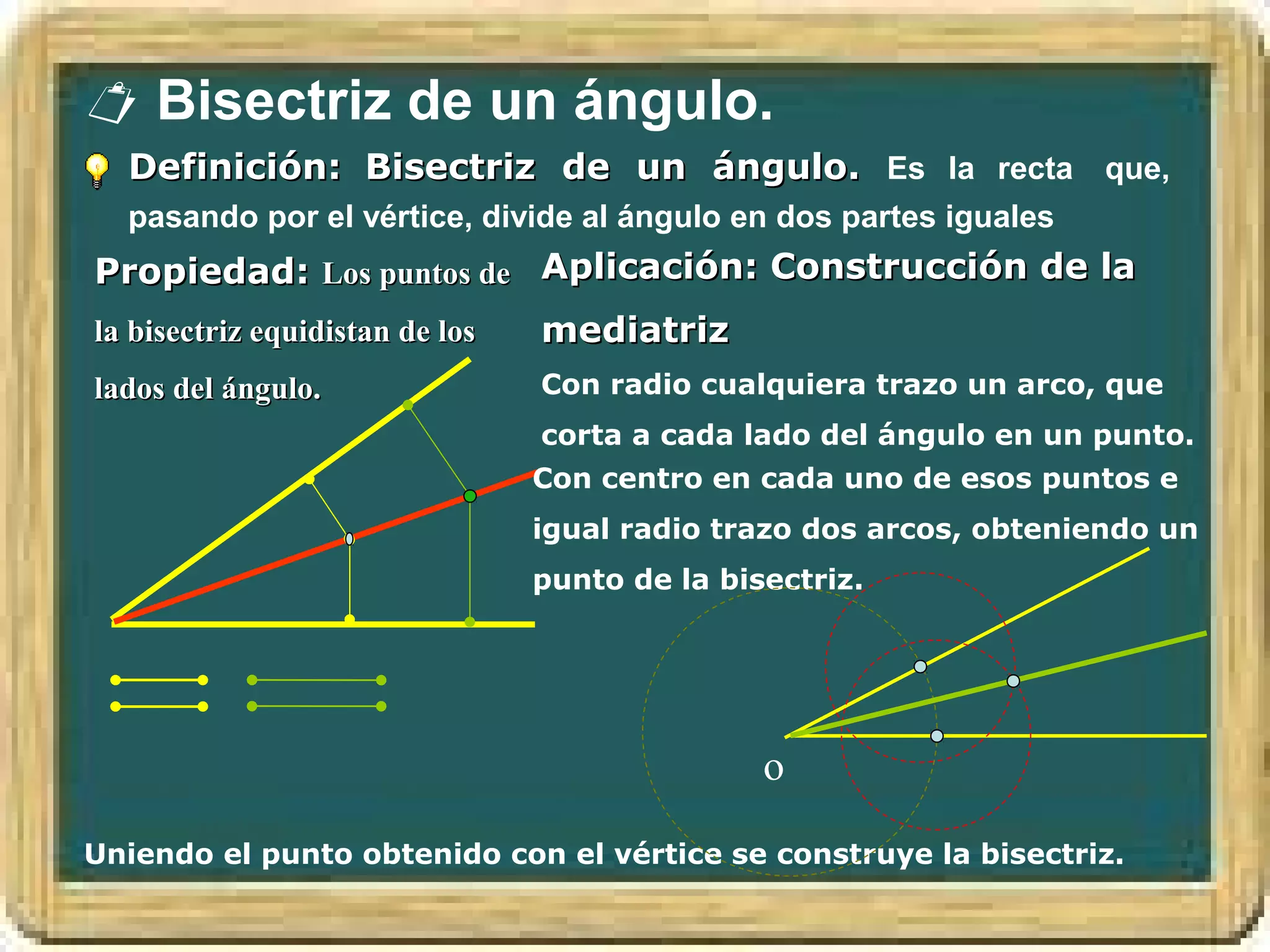
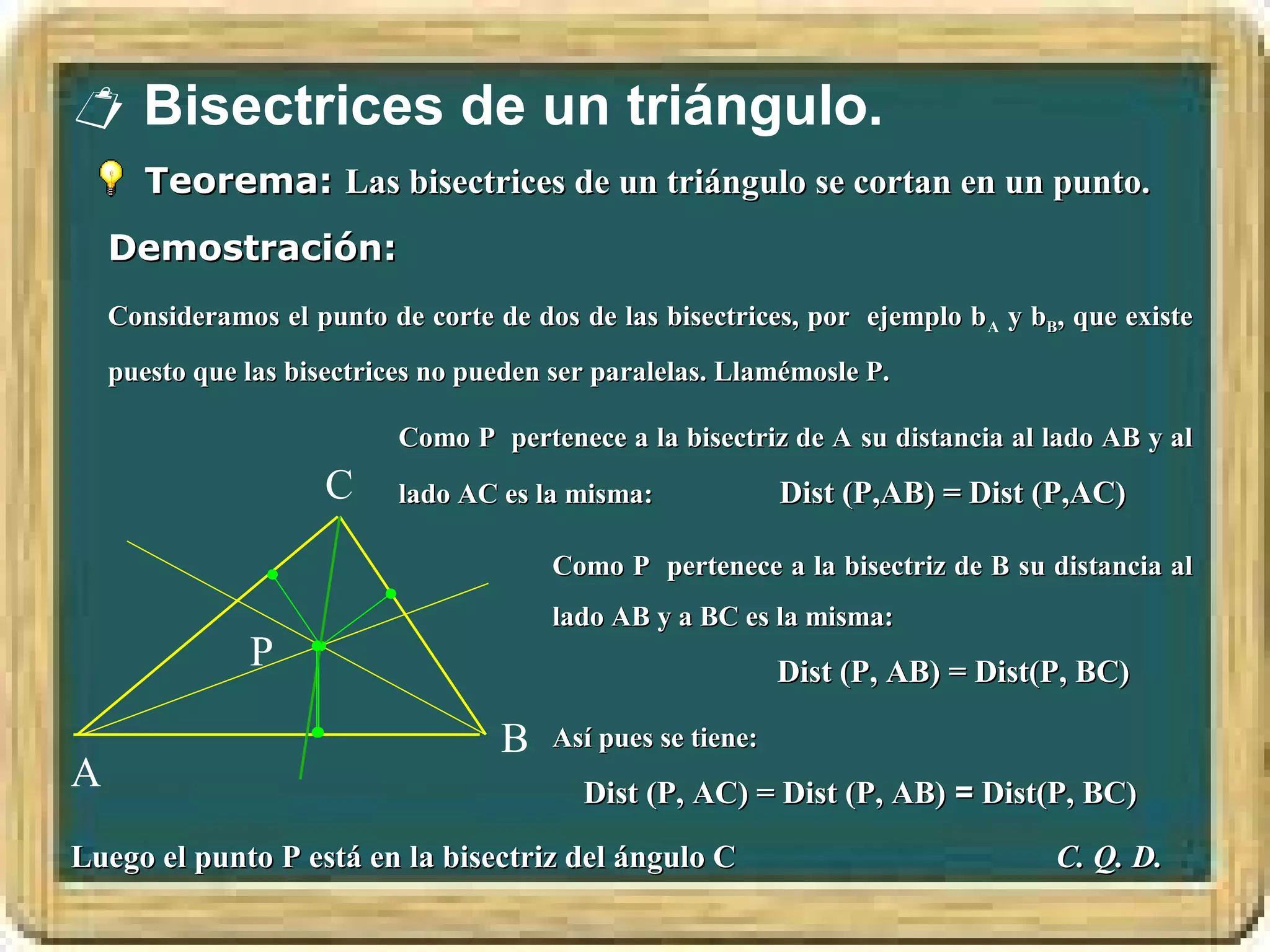
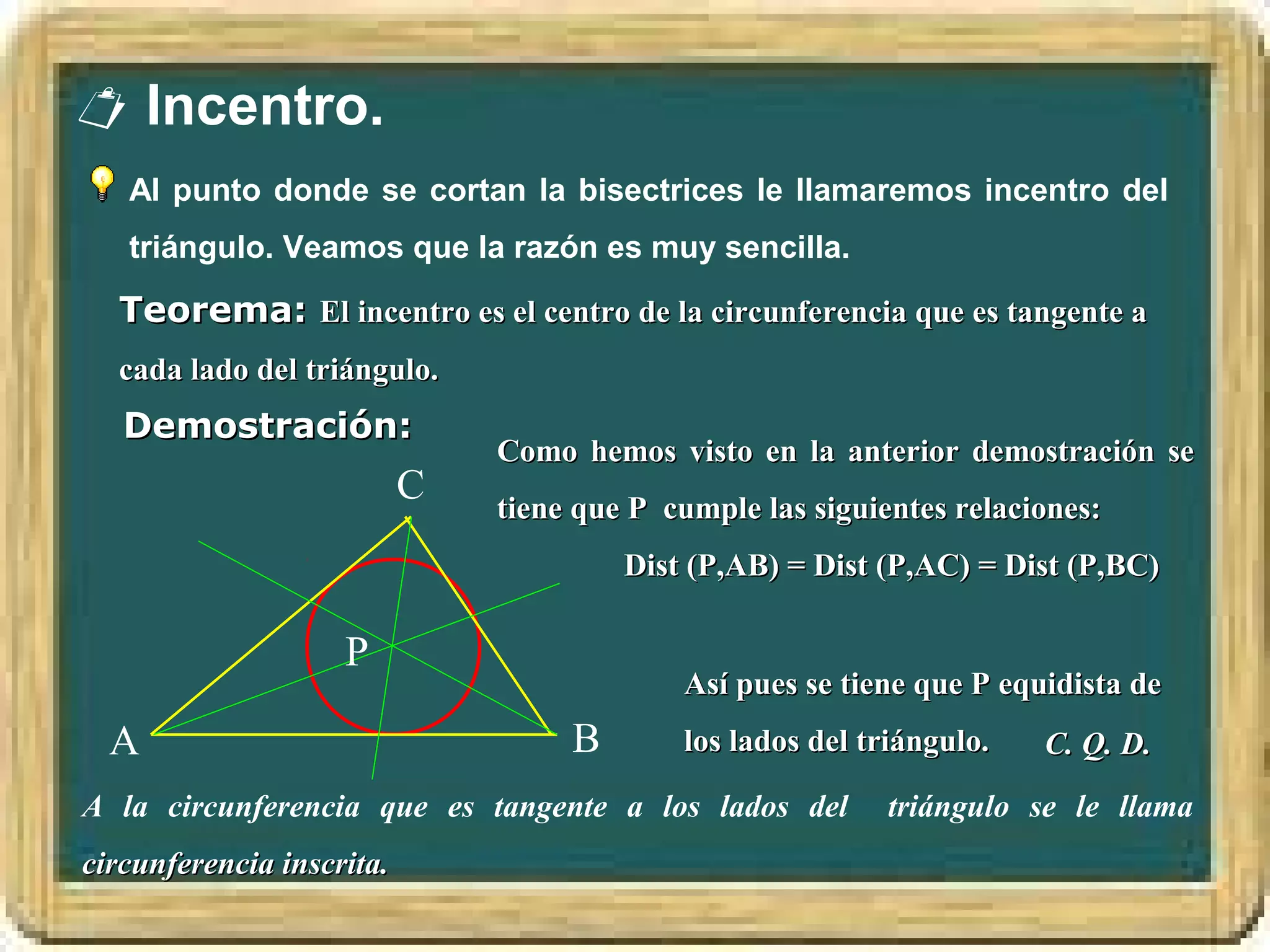
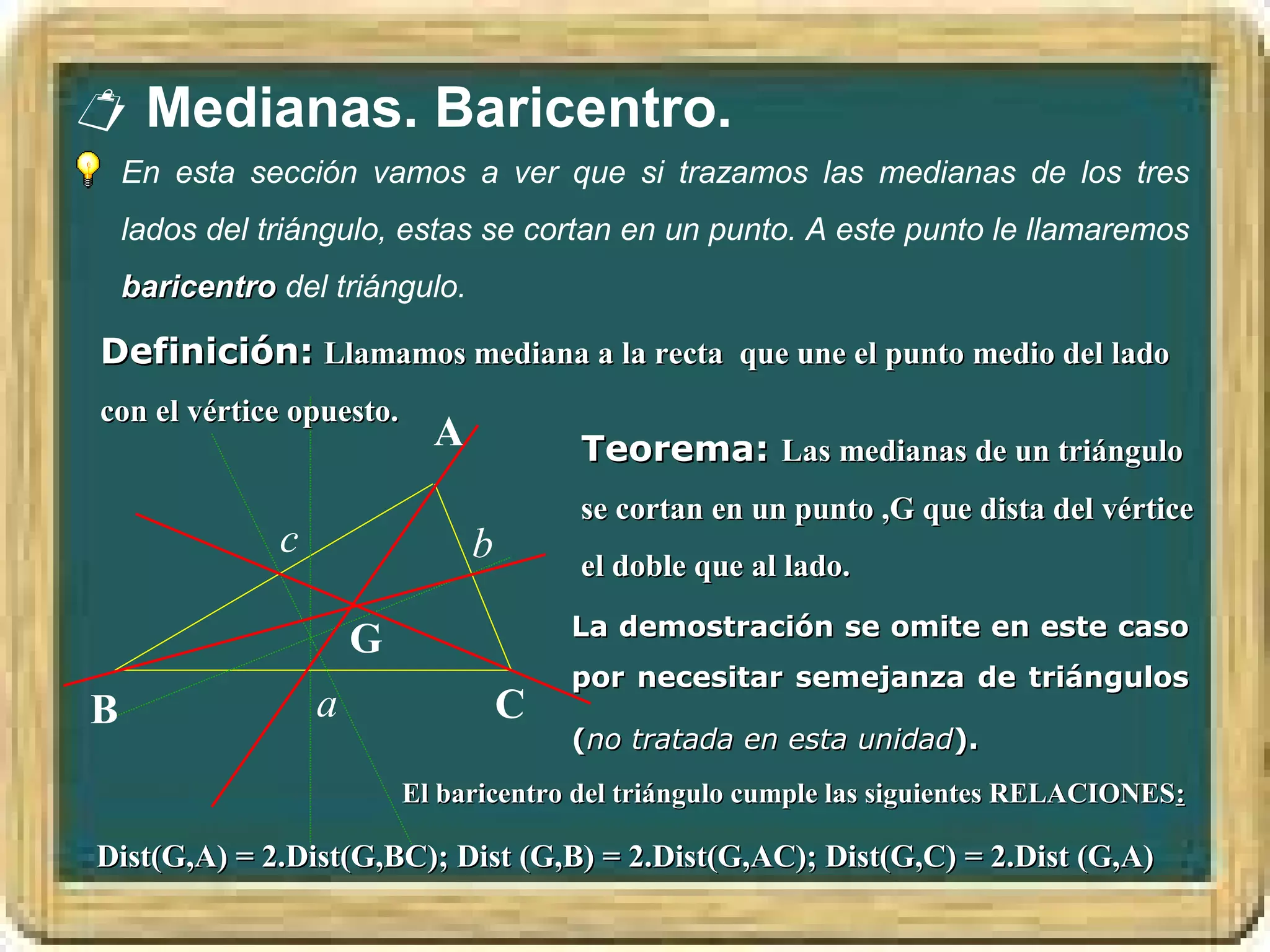
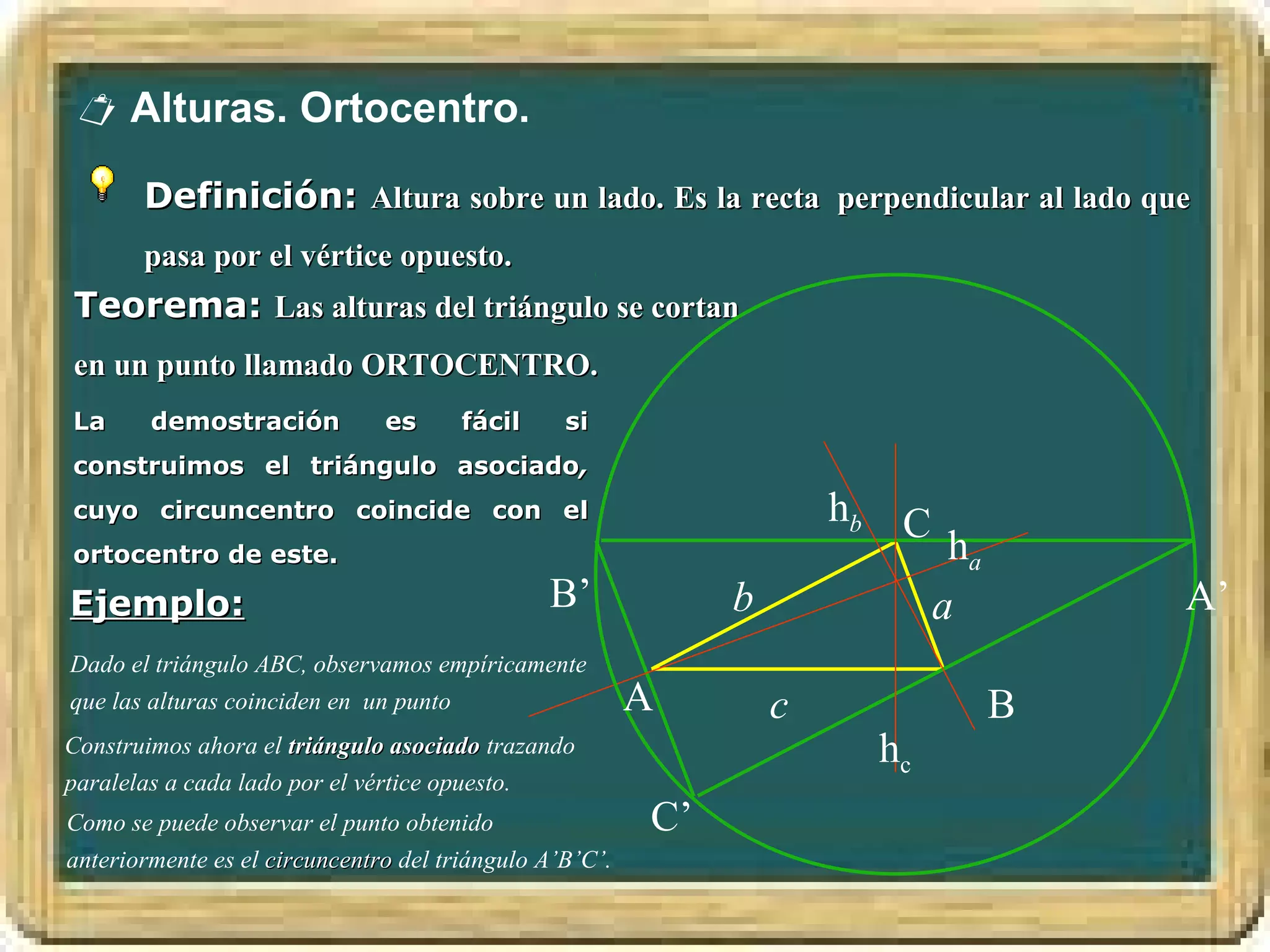
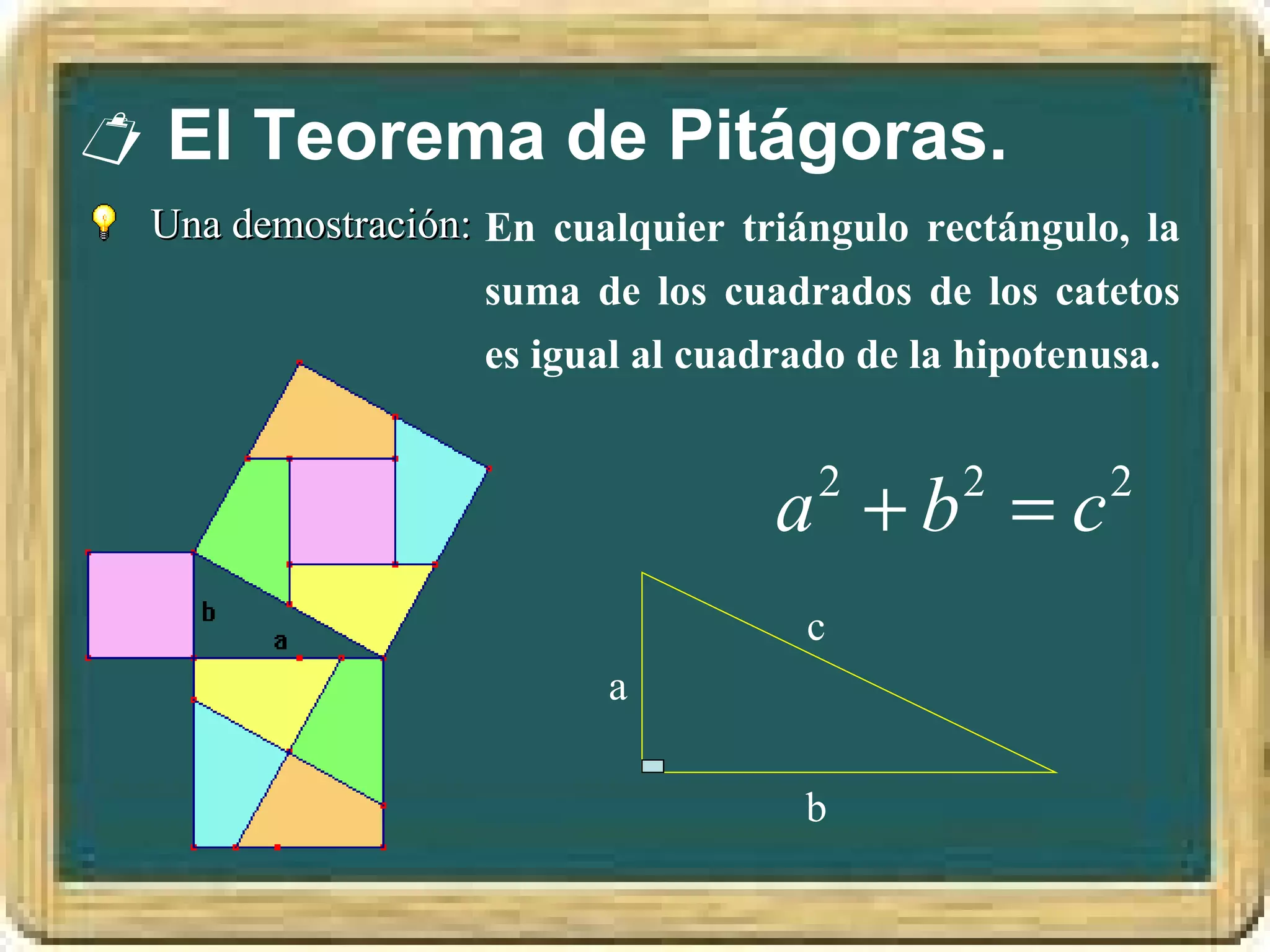
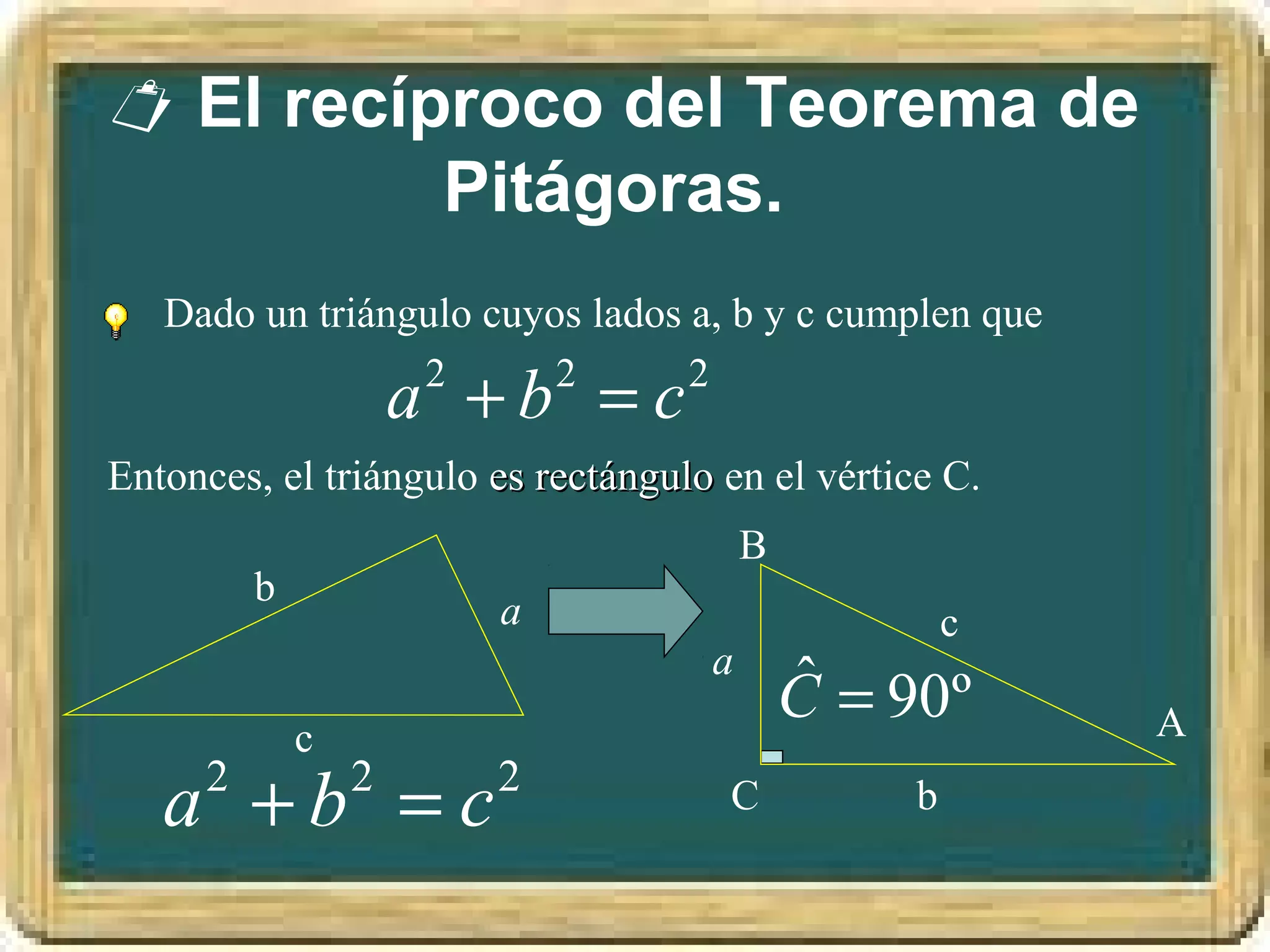
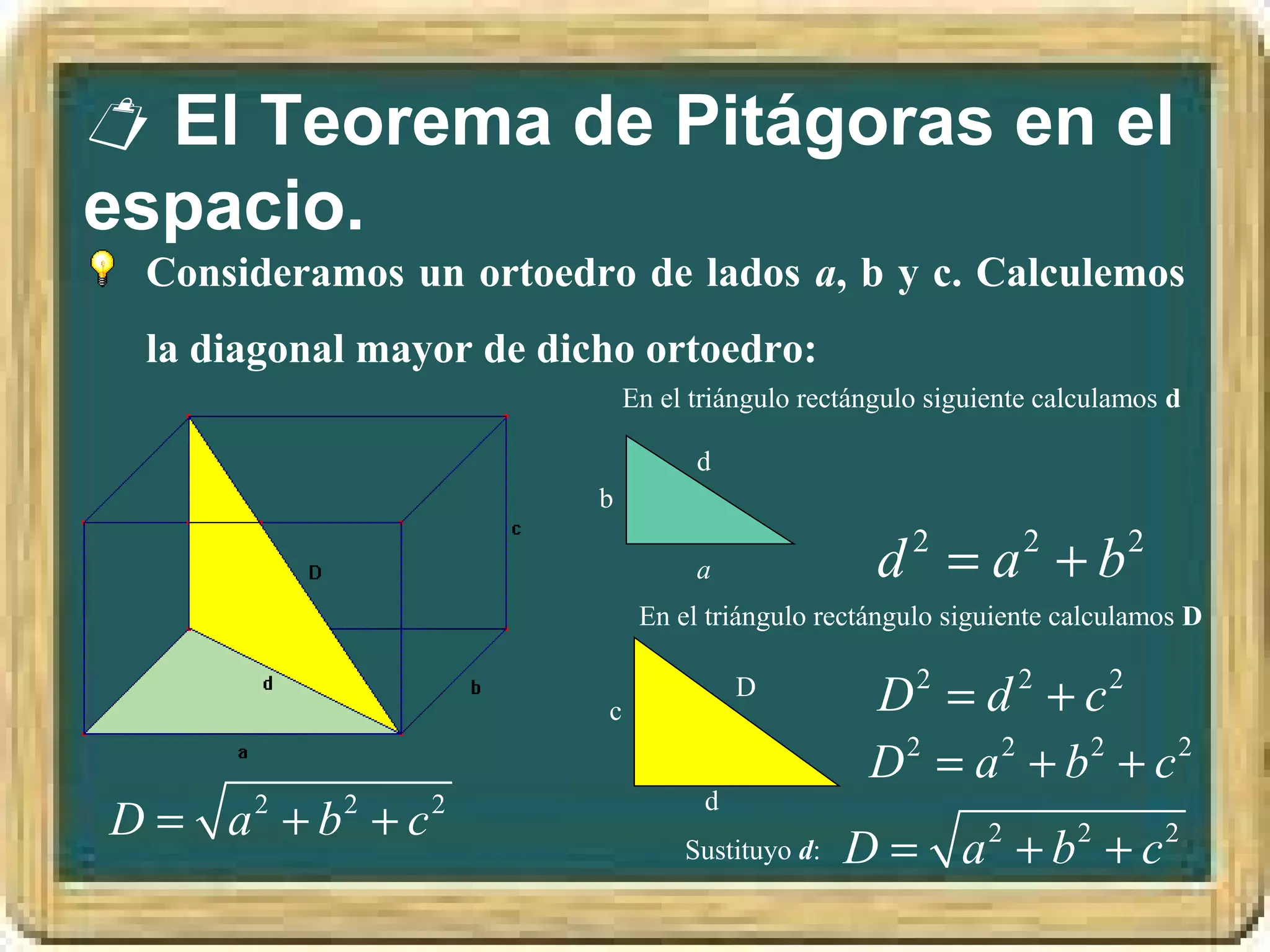
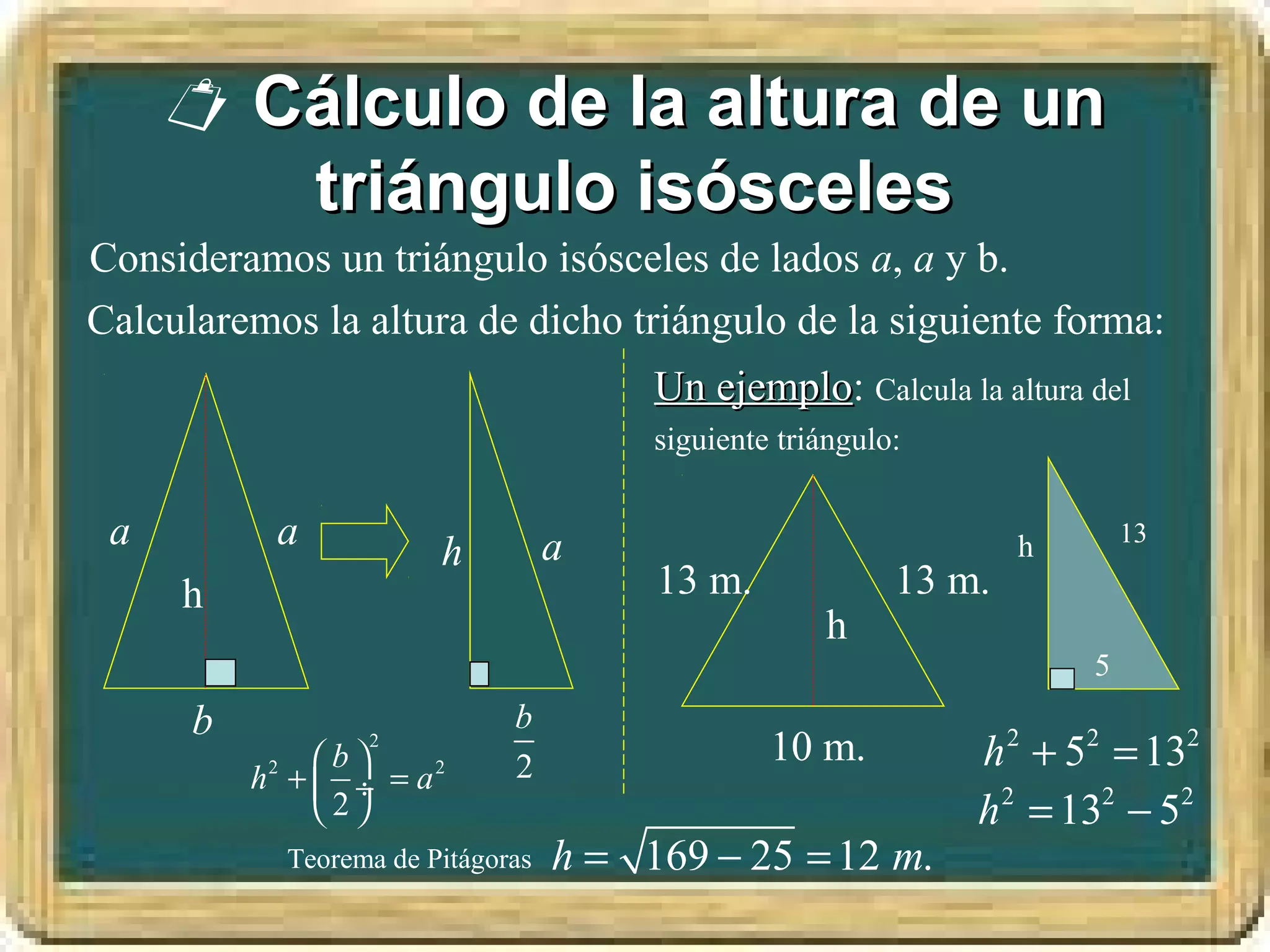
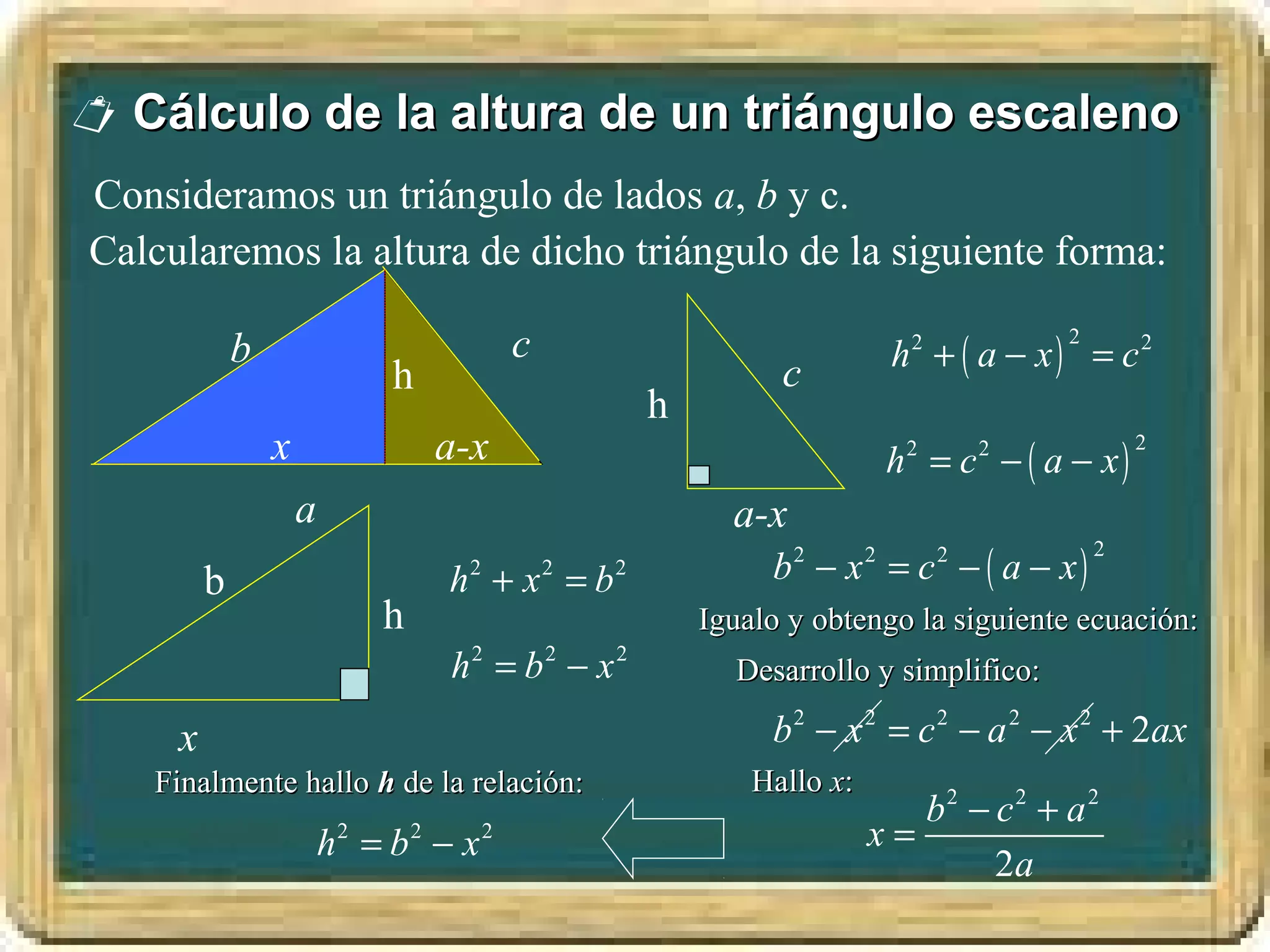
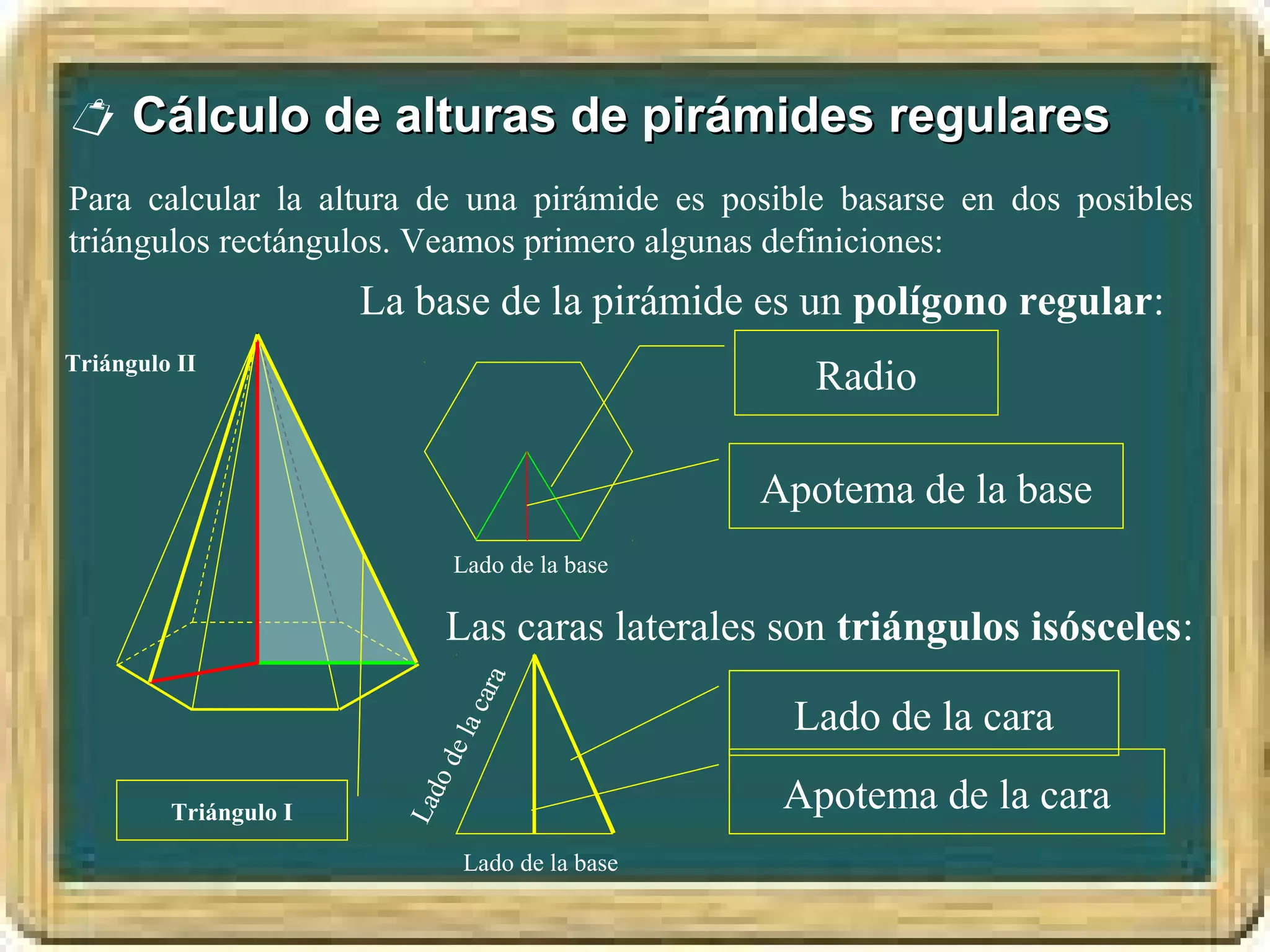
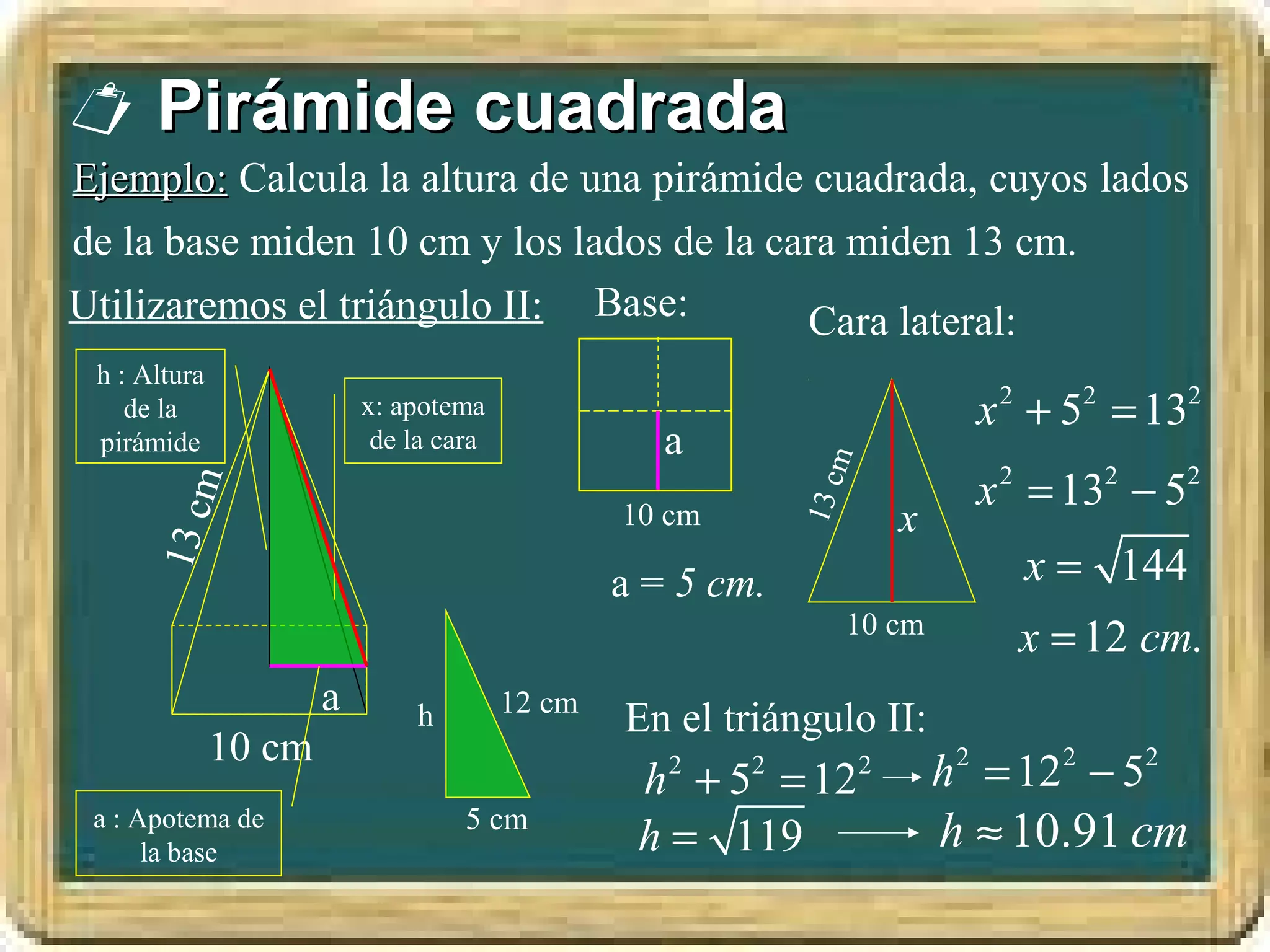
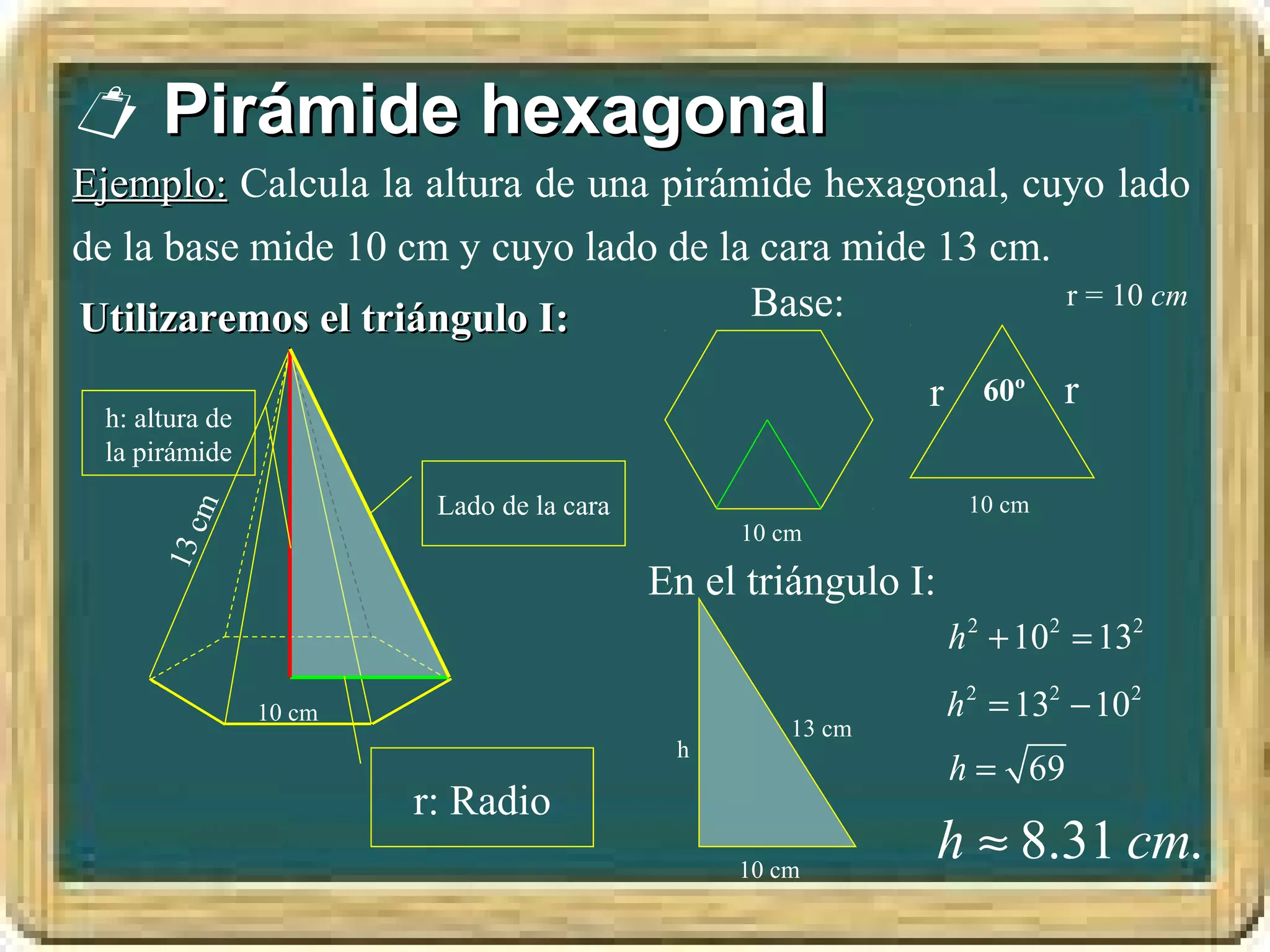
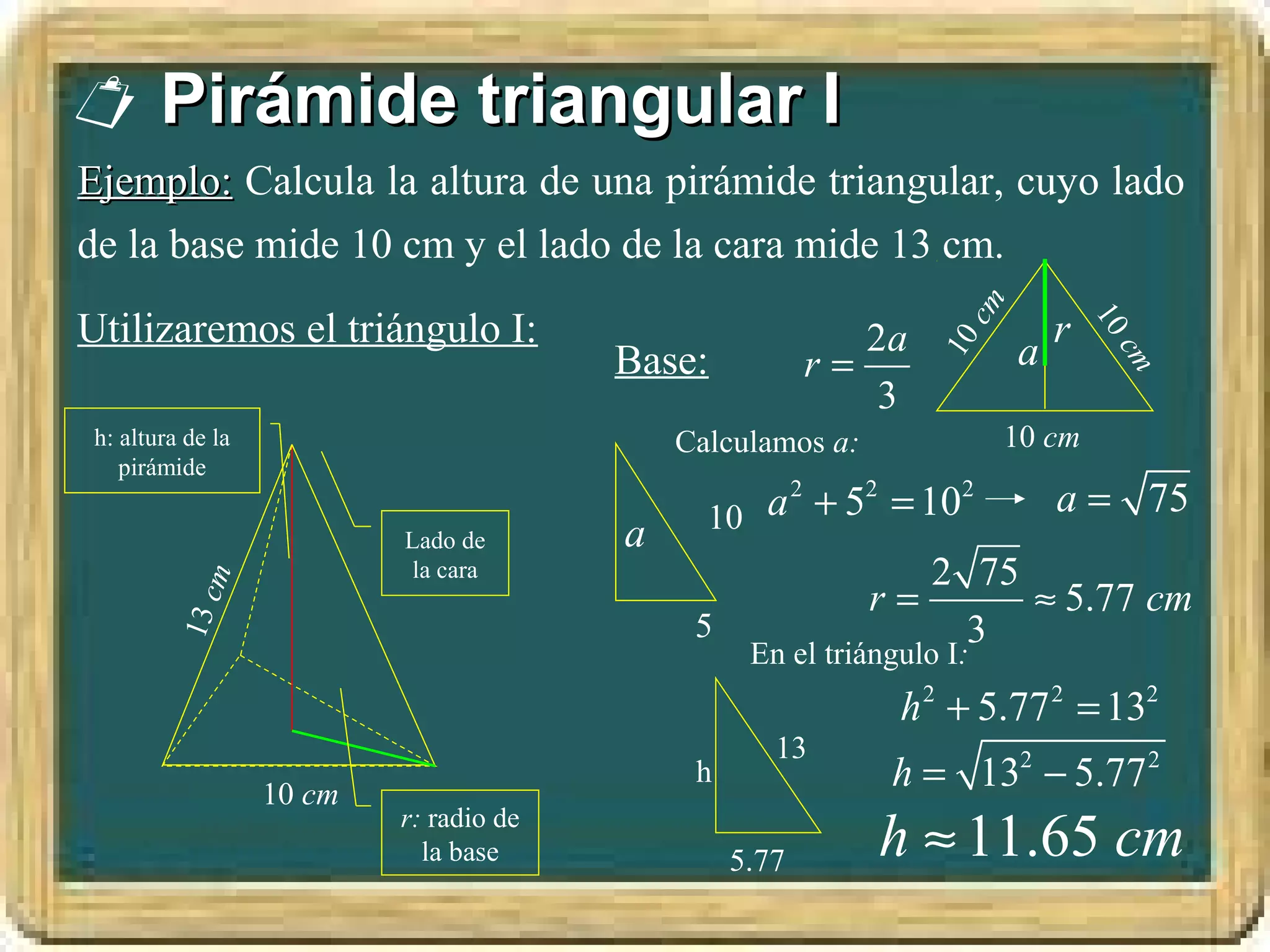
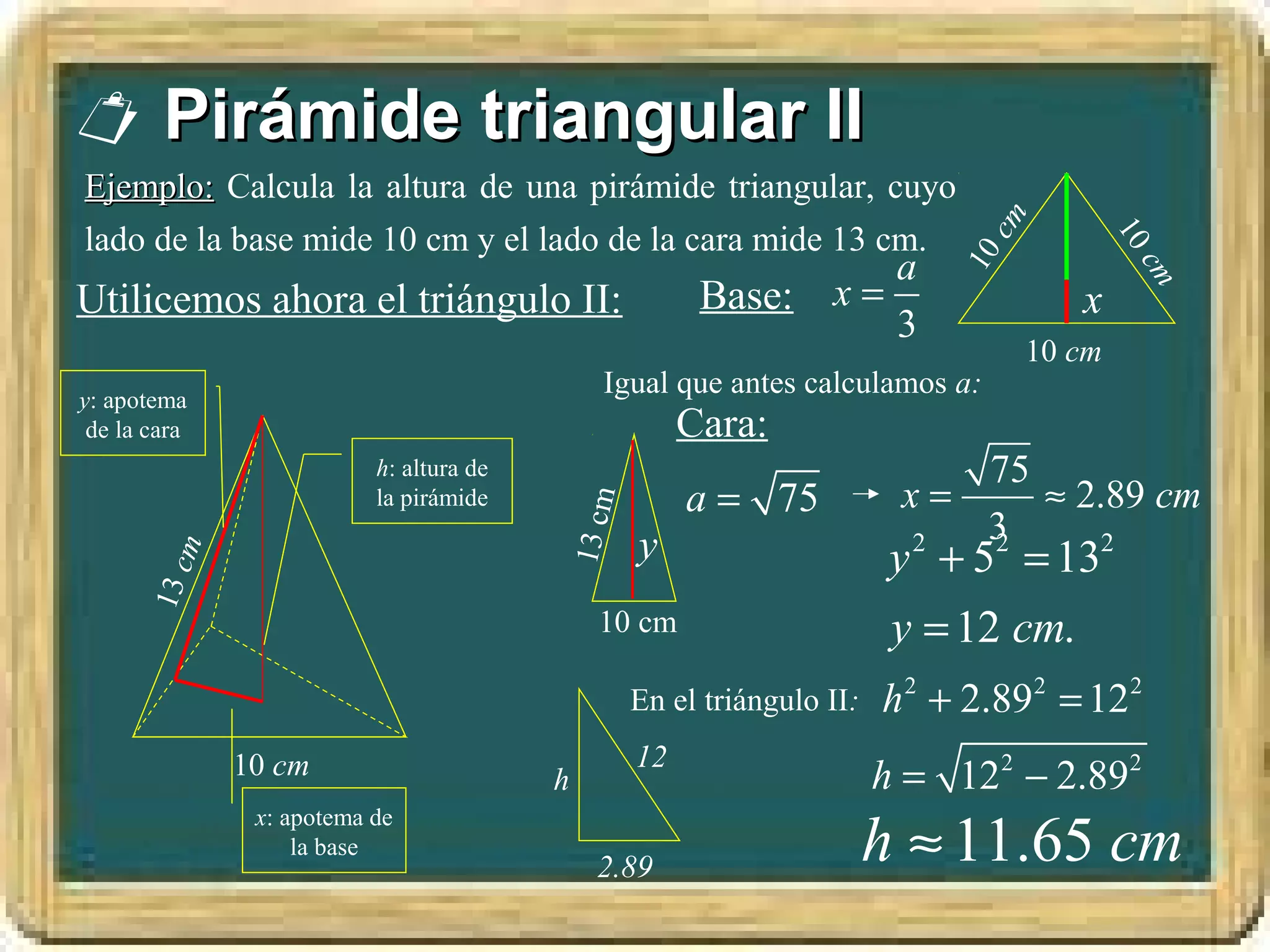
El documento resume los conceptos básicos de los triángulos, incluyendo sus elementos (vértices, lados, ángulos), tipos de triángulos, construcción de triángulos dados diferentes datos, y puntos y rectas notables como las mediatrices, bisectrices, medianas y alturas. También presenta el Teorema de Pitágoras y brinda contexto histórico sobre Pitágoras.

1. TRIÁNGULOS

2. TRIÁNGULOS
CONTENIDO DE LA PRESENTACIÓN.
• Triángulo
• Elementos
• Ángulos del triángulo
• Construcción de triángulos
• Puntos y rectas notables del triángulo
– Mediatrices. Circuncentro
– Bisectrices. Incentro.
– Medianas. Baricentro.
– Alturas. Ortocentro.
Triángulos rectángulos: Teorema de Pitágoras

3. TRIÁNGULO.
Llamamos triángulo a un conjunto de tres puntos no alineados. A estos
puntos se les llama vértices del triángulo.
Si unimos cada uno de los tres vértices mediante segmentos, a estos
segmentos se le llama lados del triángulo.
- Un triángulo se llama equilátero si tiene los tres lados iguales.
- Un triángulo se llama isósceles si tiene dos lados iguales
-Un triángulo se llama escaleno si tiene los tres lados desiguales.
Además en cada vértice del triángulo se forma un ángulo. A estos
ángulos se les llama ángulos del triángulo
- Un triángulo con los tres ángulos agudos se llama acutángulo.
- Un triángulo con un ángulo obtuso se llama obtusángulo.

4. ELEMENTOS.
El triángulo que aparece en el dibujo es un triángulo acutángulo.
En él puedes observar:
• Los vértices
• Los lados y sus medidas
• Los ángulos y sus medidas Vértice C
Lado b= AC
10,02 cm Ángulo C Lado a= BC
43,0 ° 6,24 cm
Ángulo B
Ángulo  54,7 °
68,2 °
Vértice A 13,11 cm Vértice B
Lado c = AB

5. ÁNGULOS DE UN TRIÁNGULO.
Teorema:
La suma de ángulos de un triángulo es igual a 180º
Luego la suma de ángulos de cualquier triángulo es igual a dos rectos

6. CONSTRUCCIÓN DE UN TRIÁNGULO.
A continuación veremos cuándo es posible construir un triángulo
dados tres datos de él, es decir:
 Dados tres lados.
 Dados dos lados y un ángulo.
 Dados un lado y dos ángulos.

7.  DADOS TRES LADOS.
La condición para poder construir un triángulo a partir de tres segmentos,
es: La suma de dos segmentos cualesquiera es mayor que el tercero. Esto
supone tres condiciones, que se pueden resumir: La suma de dos lados es
mayor que el tercero, y este menor que la diferencia: a+c > b > a-c
Ejemplo: a
b
c Construcción paso a paso:
1.Coloco uno de los segmentos como base
a c del triángulo
2. Con centro en cada uno de los extremos
b del segmento dibujo dos arcos:
Uno con radio a Otro con radio c
3. Se unen los extremos del segmento que he tomado como base, con el punto
de corte de los arcos y ya se tiene construido el triángulo.

8.  DADOS DOS LADOS Y UN ÁNGULO.
CASO 1 (SIEMPRE ES POSIBLE):
Conocemos dos lados y el ángulo comprendido por ellos
Ejemplo:
Construcción paso a paso:
a 1. Colocamos como base a uno de los
lados
b 2. Con el transportador de ángulos
situado en uno de los extremos de la
Ángulo comprendido = 30º base, medimos el ángulo. En nuestro
caso 30º.
3. Con esa inclinación trazamos una
recta.
b 4. Sobre la recta medimos el otro lado.
30º
5. Unimos los extremos libres de los
a dos lados.

9.  DADOS DOS LADOS Y UN ÁNGULO.
CASO 2 (POSIBLE EN ALGUNOS CASOS):
Conocemos dos lados y el ángulo adyacente a uno de ellos
Ejemplo:
a Construcción paso a paso:
b 1. Colocamos como base al lado a
2. Con el transportador de ángulos
Ángulo adyacente a a = 30º situado en uno de los extremos de la
base, medimos el ángulo. En nuestro
caso 30º.
b b 3. Con esa inclinación trazamos una recta.
30º 4. En el otro extremo del lado trazo un
arco con radio b.
a 5. El punto de corte de la recta con el
COMO PUEDES OBSERVAR EN ESTE arco, si es que este existe, da el tercer
CASO EXISTEN DOS SOLUCIONES vértice del triángulo.

10.  DADOS UN LADO Y DOS ÁNGULOS.
Para poder construir el triángulo, la suma de los dos ángulos dados
debe de ser menor de 180º
Construcción paso a paso:
1. Colocamos como base al lado
2. Con el transportador de ángulos situado en uno de los extremos de la base,
medimos uno de los ángulos y trazamos una recta con esa inclinación.
3. Hacemos lo mismo con el otro ángulo en Ejemplo: a
el otro extremo.
Ángulos adyacentes 40º y 70º
4. El punto de corte de
esas rectas es el tercer
vértice.
70º 40º
a

11.  Puntos y rectas notables del triángulo
Estudiaremos la construcción y las
propiedades de los siguientes puntos y
rectas notables de un triángulo:
Mediatrices. Circuncentro
Bisectrices. Incentro.
Medianas. Baricentro.
Alturas. Ortocentro

12.  Mediatrices.
Mediatriz de un segmento: Es la recta perpendicular al
segmento que pasa por el punto medio de dicho segmento
Propiedad: Aplicación: Construcción de la mediatriz
Los puntos de la mediatriz equidistan Con radio un poco mayor que la
mitad del segmento trazo dos arcos,
de los extremos del segmento.
cada uno con centro en cado uno del
los extremos del segmento.

13.  Mediatrices de un triángulo.
Teorema: Las mediatrices de un triángulo se cortan en un punto que
equidista de los tres vértices del triángulo.
Demostración:
Consideramos el punto de corte de dos de las
A mediatrices, por ejemplo ma y mb, que existe puesto que
los lados a y b no son paralelos. Llamémosle P.
c b
Como P pertenece a la mediatriz de a su distancia a B
B P y a C es la misma: Dist (P, B) = Dist (P, C)
C Como P pertenece a la mediatriz de b su distancia a A
a y a C es la misma: Dist (P, A) = Dist (P, C)
Así pues se tiene que P pertenece a la mediatriz mc y se cumple:
Dist (P,B) = Dist (P,A) = Dist (P,C)
Luego el punto P es el punto de intersección de las tres mediatrices y equidista de
los tres vértices C.Q.D.

14.  Circuncentro de un triángulo.
Al punto donde se cortan la mediatrices le llamaremos circuncentro
del triángulo. Veamos que la razón es muy sencilla.
Teorema:
El circuncentro es el centro de la circunferencia que pasa por los tres vértices.
A Demostración:
b Como hemos visto en la anterior
c
demostración se tiene que P cumple las
P
siguientes relaciones:
B C
a Dist (P,A) = Dist (P,B) = Dist (P,C)
Así pues se tiene que P equidista de los tres vértices
del triángulo. Y por tanto es el centro de la
circunferencia que pasa por los tres vértices C. Q. D.
A la circunferencia que pasa por los tres vértices se le llama circunferencia circunscrita.

15.  Bisectriz de un ángulo.
Definición: Bisectriz de un ángulo. Es la recta que,
pasando por el vértice, divide al ángulo en dos partes iguales
Propiedad: Los puntos de Aplicación: Construcción de la
la bisectriz equidistan de los mediatriz
lados del ángulo. Con radio cualquiera trazo un arco, que
corta a cada lado del ángulo en un punto.
Con centro en cada uno de esos puntos e
igual radio trazo dos arcos, obteniendo un
punto de la bisectriz.
o
Uniendo el punto obtenido con el vértice se construye la bisectriz.

16.  Bisectrices de un triángulo.
Teorema: Las bisectrices de un triángulo se cortan en un punto.
Demostración:
Consideramos el punto de corte de dos de las bisectrices, por ejemplo b A y bB, que existe
puesto que las bisectrices no pueden ser paralelas. Llamémosle P.
Como P pertenece a la bisectriz de A su distancia al lado AB y al
C lado AC es la misma: Dist (P,AB) = Dist (P,AC)
Como P pertenece a la bisectriz de B su distancia al
lado AB y a BC es la misma:
P Dist (P, AB) = Dist(P, BC)
B Así pues se tiene:
A Dist (P, AC) = Dist (P, AB) = Dist(P, BC)
Luego el punto P está en la bisectriz del ángulo C C. Q. D.

17.  Incentro.
Al punto donde se cortan la bisectrices le llamaremos incentro del
triángulo. Veamos que la razón es muy sencilla.
Teorema: El incentro es el centro de la circunferencia que es tangente a
cada lado del triángulo.
Demostración:
Como hemos visto en la anterior demostración se
C tiene que P cumple las siguientes relaciones:
Dist (P,AB) = Dist (P,AC) = Dist (P,BC)
P
Así pues se tiene que P equidista de
A B los lados del triángulo. C. Q. D.
A la circunferencia que es tangente a los lados del triángulo se le llama
circunferencia inscrita.

18.  Medianas. Baricentro.
En esta sección vamos a ver que si trazamos las medianas de los tres
lados del triángulo, estas se cortan en un punto. A este punto le llamaremos
baricentro del triángulo.
Definición: Llamamos mediana a la recta que une el punto medio del lado
con el vértice opuesto.
A Teorema: Las medianas de un triángulo
se cortan en un punto ,G que dista del vértice
c b el doble que al lado.
La demostración se omite en este caso
G
por necesitar semejanza de triángulos
B a C
(no tratada en esta unidad).
El baricentro del triángulo cumple las siguientes RELACIONES:
Dist(G,A) = 2.Dist(G,BC); Dist (G,B) = 2.Dist(G,AC); Dist(G,C) = 2.Dist (G,A)

19.  Alturas. Ortocentro.
Definición: Altura sobre un lado. Es la recta perpendicular al lado que
pasa por el vértice opuesto.
Teorema: Las alturas del triángulo se cortan
en un punto llamado ORTOCENTRO.
La demostración es fácil si
construimos el triángulo asociado,
cuyo circuncentro coincide con el hb C
ortocentro de este. ha
Ejemplo: B’ b a A’
Dado el triángulo ABC, observamos empíricamente
que las alturas coinciden en un punto A c B
Construimos ahora el triángulo asociado trazando hc
paralelas a cada lado por el vértice opuesto.
Como se puede observar el punto obtenido C’
anteriormente es el circuncentro del triángulo A’B’C’.

20.  La recta de Euler.
En esta sección vamos a ver que baricentro, circuncentro y ortocentro
siempre están alineados. Es más el baricentro siempre se encuentra entre
el ortocentro y el circuncentro y además cumple una curiosa propiedad.
Propiedad: Sean G el baricentro, C el circuncentro y O
el ortocentro del triángulo, entonces
uuur uuur
GO = −2 ×GC
Además se puede probar que el incentro está alineado con
estos tres cuando y sólo cuando el triángulo es isósceles.
A la recta que contiene a los tres puntos
notables se le llama RECTA DE EULER.

21. EL TEOREMA DE PITÁGORAS. Pitágoras de Samos (580-500 aC.)
Es un personaje aún más misterioso que Thales. Vivió unos 50 años
después de éste y, en su juventud, viajó por Egipto, Babilonia y posiblemente la
India, países en los que adquirió su formación matemática y filosófica.
Contemporáneo de Buda, Confucio y Lao Tse, estuvo muy influido por el misticismo
religioso. Se estableció en Crotona, al sudeste de Italia, entonces, parte de Grecia,
donde fundó una secta secreta, los pitagóricos, que contribuyeron en el mundo
pitagóricos
heleno a la difusión y desarrollo de las matemáticas. La primera referencia escrita
vuelve a aparecer en la obra de Proclo (410-485dC) "Comentario sobre el primer
libro de los Elementos de Euclides". Inmediatamente después de escribir sobre
Thales, Proclo escribe: "transformó esta ciencia en una forma de educación liberal,
examinando sus principios desde el comienzo y demostrando los teoremas de una
manera inmaterial e intelectual. Así descubrió la teoría de las proporciones y la
construcción de las figuras cósmicas". Fueron los pitagóricos los primeros que se
dedicaron al estudio, movidos por el amor a la sabiduría y la belleza y no por
cuestiones de tipo práctico. Parece que es difícil separar la historia y la leyenda en lo
que se refiere a Pitágoras, pero sí está clara la influencia de su escuela en el
desarrollo de la matemática griega.
Parece ser que la estrella de cinco puntas construida a partir de un pentágono
regular era el símbolo de los miembros de la secta. Estudiando las propiedades de los
segmentos de esta estrella podemos encontrar la llamada sección áurea.
Se les atribuye la demostración del teorema de Pitágoras, conocido también por los
babilónicos, pero no existe una prueba clara de esto.

22.  El Teorema de Pitágoras.
Una demostración: En cualquier triángulo rectángulo, la
suma de los cuadrados de los catetos
es igual al cuadrado de la hipotenusa.
a +b =c
2 2 2
c
a
b

23.  El recíproco del Teorema de
Pitágoras.
Dado un triángulo cuyos lados a, b y c cumplen que
2
a +b =c
2 2
Entonces, el triángulo es rectángulo en el vértice C.
B
b
a c
a
ˆ
C = 90º
c A
a +b =c
2 2 2 C b

24.  El Teorema de Pitágoras en el
espacio.
Consideramos un ortoedro de lados a, b y c. Calculemos
la diagonal mayor de dicho ortoedro:
En el triángulo rectángulo siguiente calculamos d
d
b
a d 2 = a 2 + b2
En el triángulo rectángulo siguiente calculamos D
c
D
D2 = d 2 + c2
D2 = a 2 + b2 + c2
d
D = a +b +c
2 2 2
Sustituyo d: D = a 2 + b2 + c 2

25. Aplicaciones del teorema de
Pitágoras
• Cálculo de la altura en triángulos
isósceles
• Cálculo de la altura en triángulos
escalenos
• Cálculo de la altura de una pirámide

26.  Cálculo de la altura de un
triángulo isósceles
Consideramos un triángulo isósceles de lados a, a y b.
Calcularemos la altura de dicho triángulo de la siguiente forma:
Un ejemplo: Calcula la altura del
ejemplo
siguiente triángulo:
a a h a h 13
h 13 m. 13 m.
h
5
b b
b
2
2
10 m. h 2 + 52 = 132
h2 +  ÷ = a 2
2 h 2 = 132 − 52
Teorema de Pitágoras h = 169 − 25 = 12 m.

27.  Cálculo de la altura de un triángulo escaleno
Consideramos un triángulo de lados a, b y c.
Calcularemos la altura de dicho triángulo de la siguiente forma:
c h2 + ( a − x ) = c 2
2
b
h c
h
x a-x h = c − ( a − x)
2 2 2
a a-x
b − x = c − ( a − x)
2 2 2 2
b h +x =b
2 2 2
h Igualo y obtengo la siguiente ecuación:
h2 = b2 − x 2 Desarrollo y simplifico:
x b 2 − x 2 = c 2 − a 2 − x 2 + 2ax
Finalmente hallo h de la relación: Hallo x:
b2 − c2 + a 2
h2 = b2 − x 2 x=
2a

28.  Un ejemplo.
Planteo la ecuación y la resuelvo:
4m 5m 16 − x 2 = 25 − 49 − x 2 + 14 x
h 16 = 25 − 49 + 14x
x 7-x
16 − 25 + 49 40 20
7m x= = =
14 14 7
h 2 + x 2 = 42
4 h 2 = 16 − x 2 Por último hallo h:
h 2
 20  400 384
h 2 = 16 − x 2 = 16 −  ÷ = 16 − =
x  7  49 49
h + ( 7 − x ) = 52
2 2
5
h = 25 − ( 7 − x ) 384
2 2
h h= ≈2, 799
49
7-x
La altura del triángulo es aproximadamente 2’8 m.

29.  Cálculo de alturas de pirámides regulares
Para calcular la altura de una pirámide es posible basarse en dos posibles
triángulos rectángulos. Veamos primero algunas definiciones:
La base de la pirámide es un polígono regular:
Triángulo II
Radio
Apotema de la base
Lado de la base
Las caras laterales son triángulos isósceles:
ara
Lado de la cara
la c
de
Apotema de la cara
o
Lad
Triángulo I
Lado de la base

30.  Pirámide cuadrada
Ejemplo: Calcula la altura de una pirámide cuadrada, cuyos lados
de la base miden 10 cm y los lados de la cara miden 13 cm.
Utilizaremos el triángulo II: Base: Cara lateral:
h : Altura
de la x: apotema x 2 + 52 = 132
pirámide de la cara a
m
x 2 = 132 − 52
m
13 c
10 cm x
13 c
a = 5 cm. x = 144
10 cm
x = 12 cm.
a 12 cm
h En el triángulo II:
10 cm
h + 5 = 12
2 2 2 h 2 = 122 − 52
a : Apotema de
la base
5 cm
h = 119 h ≈ 10.91 cm

31.  Pirámide hexagonal
Ejemplo: Calcula la altura de una pirámide hexagonal, cuyo lado
de la base mide 10 cm y cuyo lado de la cara mide 13 cm.
Base: r = 10 cm
Utilizaremos el triángulo I:
r 60º r
h: altura de
la pirámide
Lado de la cara 10 cm
cm
10 cm
13
En el triángulo I:
h 2 + 102 = 132
10 cm h 2 = 132 − 102
13 cm
h
h = 69
r: Radio
10 cm
h ≈ 8.31 cm.

32.  Pirámide triangular I
Ejemplo: Calcula la altura de una pirámide triangular, cuyo lado
de la base mide 10 cm y el lado de la cara mide 13 cm.
cm
Utilizaremos el triángulo I: r
10
2a a
10
Base: r=
cm
3
h: altura de la Calculamos a: 10 cm
pirámide
10 a 2 + 52 = 102 a = 75
Lado de a
la cara 2 75
m
r= ≈ 5.77 cm
13 c
5 3
En el triángulo I:
h 2 + 5.77 2 = 132
13
10 cm
h h = 132 − 5.77 2
r: radio de
la base 5.77 h ≈ 11.65 cm

33.  Pirámide triangular II
Ejemplo: Calcula la altura de una pirámide triangular, cuyo
cm
lado de la base mide 10 cm y el lado de la cara mide 13 cm.
10
a
10
cm
Utilicemos ahora el triángulo II: Base: x = x
3
10 cm
y: apotema
Igual que antes calculamos a:
de la cara Cara:
h: altura de 75
la pirámide a = 75 x= ≈ 2.89 cm
13 cm
y 3
y 2 + 5 = 13
2 2
m
13 c
10 cm y = 12 cm.
En el triángulo II: h 2 + 2.892 = 122
12
10 cm h h = 122 − 2.892
h ≈ 11.65 cm
x: apotema de
la base
2.89

34. Mas ayuda del tema de la página
Matemática de DESCARTES del
Ministerio de Educación y ciencia
(http://recursostic.educacion.es/descartes/web/)
En la siguiente diapósitiva