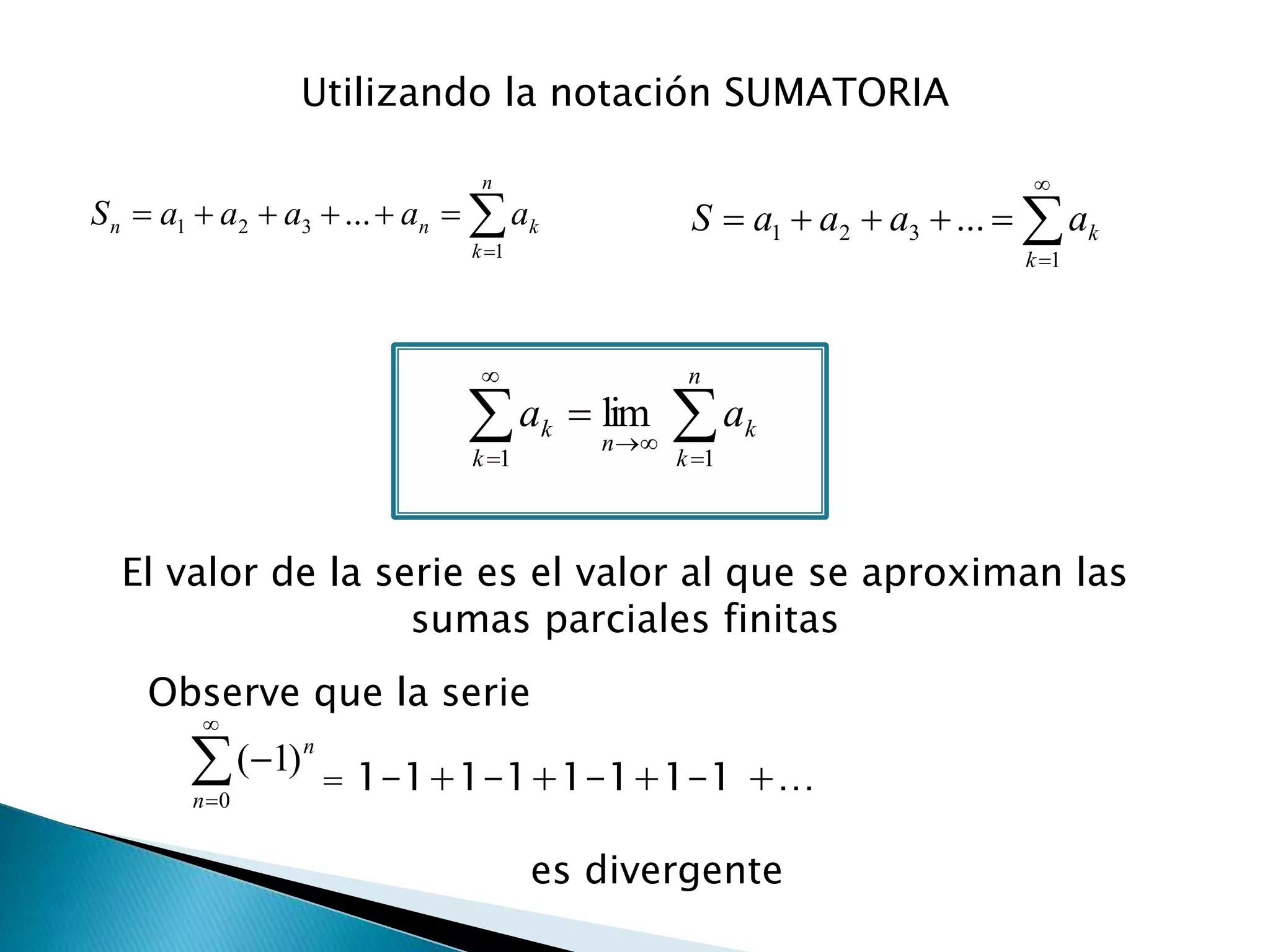
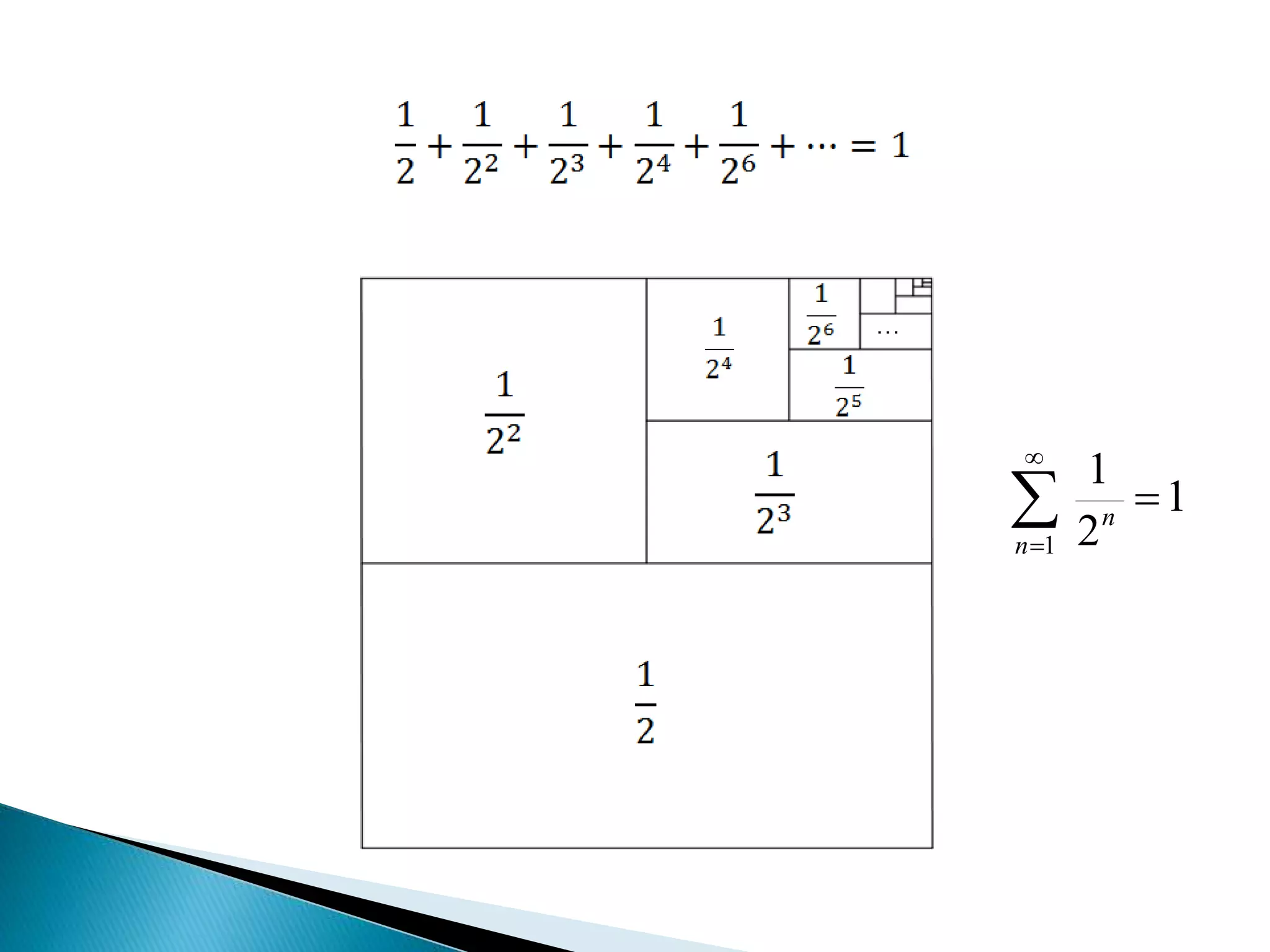
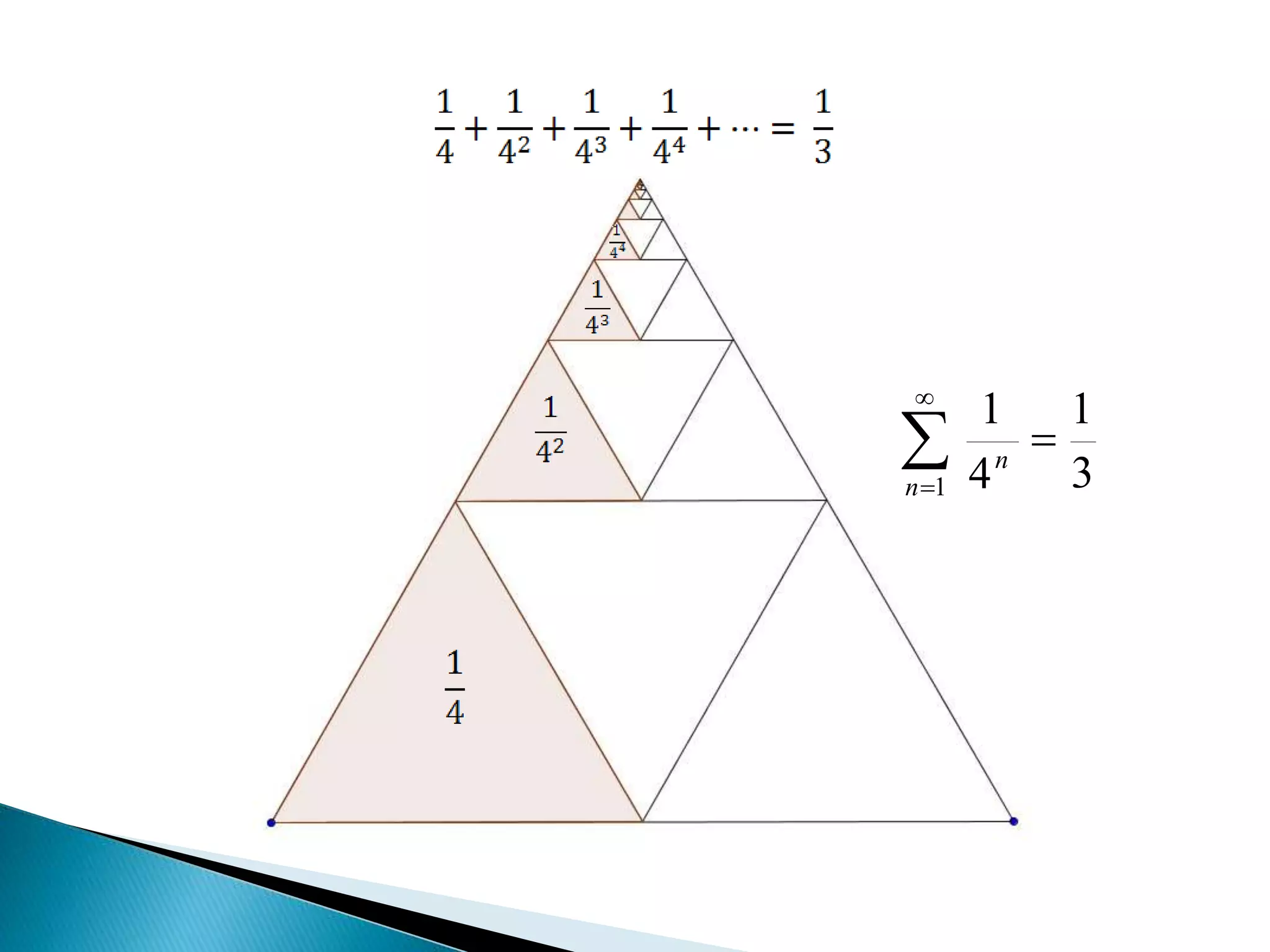
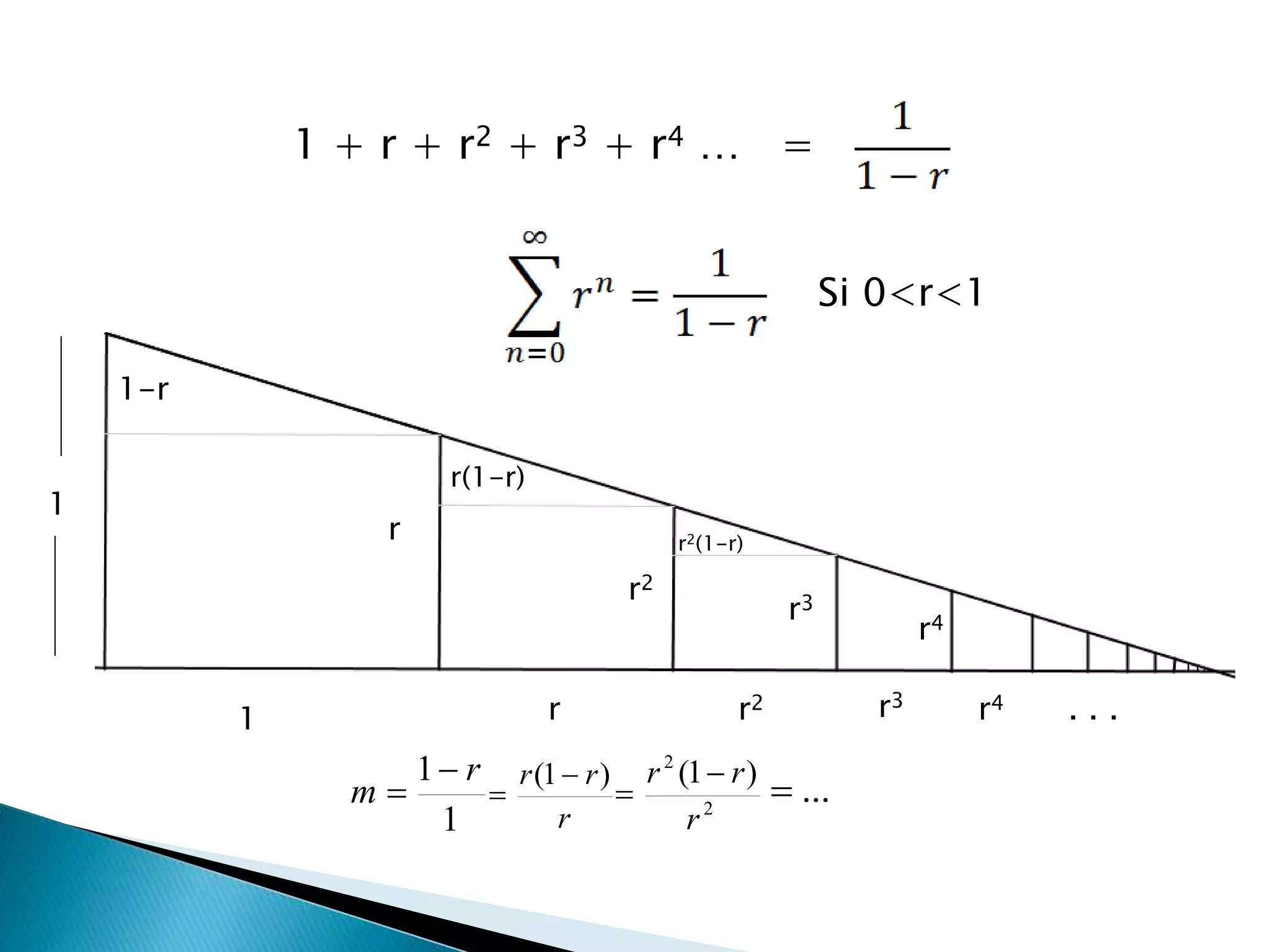
El documento introduce el concepto de series numéricas y cómo se pueden utilizar para sumar infinitas cantidades de números. Explica que algunas series como 1 + 1 + 1 + ... son divergentes, mientras que otras como 0 + 0 + 0 + ... son convergentes. También analiza ejemplos como series geométricas y armónicas, y establece criterios para determinar si una serie es convergente o divergente.

1. Jesús Meza Mauricio

2. 

1n
na...4321  aaaa =
Con el concepto de SERIE NUMÉRICA, queremos darle sentido
a la SUMA de una infinidad de números reales.
Pero… ¿Qué situaciones nos llevan a esto?
¿Es que acaso alguna vez hemos tenido que sumar una infinidad
de números?
Series Numéricas

3. Aunque no tengamos una definición matemáticamente precisa de
cómo realizar estas sumas, no tenemos ninguna duda en que …
1 + 1 + 1 + 1 + 1 + …
… tendrá un valor infinito, es decir NO se pueden sumar, en el
sentido de que la suma sea un número real.
En este caso diremos que la SERIE ES DIVERGENTE.
También, sin lugar a dudas podremos decir que las siguientes
sumas, si pueden efectuarse.
0 + 0 + 0 + 0 + 0 + … = 0
1 + 0 + 0 + 0 + 0 + … =1
… y diremos que estas SERIES SON CONVERGENTES

4. … Pero, ¿qué podemos decir de la siguiente suma infinita?
1 - 1 + 1 - 1 + 1 - 1 + 1 - 1 + ...
¿Podríamos decir que es cero, agrupando de la siguiente manera?
(1 - 1) + (1 - 1) + (1 - 1) + (1 - 1) + ... = 0 + 0 + 0 + 0 + ... = 0
Si así fuera, también podríamos decir que toma el valor uno …
1 - (1 - 1) - (1 - 1) - (1 - 1) - ... = 1 - 0 - 0 - 0 - 0 - ... =1
Es razonable pedir que, si los términos de una serie se pueden sumar,
el valor de la suma sea único y, en este caso, tendríamos dos
posibles valores para la suma, lo cual nos lleva a concluir que esta
serie no es posible sumarla. Otra conclusión inmediata es que, para
sumas infinitas, no es válida la propiedad asociativa.

5. Volvamos a una de las preguntas iniciales:
¿Es que acaso alguna vez hemos tenido que sumar una
infinidad de números?
Desde la educación primaria, aprendimos que al dividir 1
entre 3, utilizando el algoritmo de la división:
0. 3 3 3 …
3 1
1 0
1 0
1
…

6. Podemos expresar a 1/3 como un decimal infinito (periódico)
O bien atendiendo la notación decimal
...
10
3
10
3
10
3
...333.0
3
1
32

Podemos expresar a 1/3 como una SERIE
Es decir, desde nuestros primeros contactos con la aritmética ha
estado presente, aunque de manera implícita, el concepto de
suma infinita.

7. Definición: Sea una sucesión de números reales.
La expresión
se llama SERIE NUMÉRICA.
A partir de la sucesión formamos una nueva sucesión de sumas
parciales
, , , …
y diremos que la serie es CONVERGENTE (sus términos se pueden
sumar) si existe.
En este caso el valor de la serie es:
De lo contrario diremos que la serie es DIVERGENTE (sus términos
no se pueden sumar).
 
1nna
...321  aaa
11 aS  212 aaS  3213 aaaS  nn aaaaS  ...321
n
n
S

lim
n
n
SS

 lim

8.  




n
k
k
n
k
k aa
11
lim


n
k
knn aaaaaS
1
321 ... 



1
321 ...
k
kaaaaS
El valor de la serie es el valor al que se aproximan las
sumas parciales finitas
Observe que la serie
= 1-1+1-1+1-1+1-1 +…
es divergente




0
)1(
n
n
Utilizando la notación SUMATORIA

9. Observe que para que una serie converja, es necesario que su
término n-ésimo sea cada vez más pequeño y cercano a cero,
es decir,


1n
na 0lim 

n
n
aconverge, 
Sin embargo, la condición no es suficiente como se ve en el
siguiente ejemplo:
...
4
1
4
1
4
1
4
1
3
1
3
1
3
1
2
1
2
1
1 
En esta serie, él término n-ésimo tiende a cero y la serie
claramente es divergente.

10. …




1
1
2
1
n
n

11. 



1 3
1
4
1
n
n

12. 1
1 r r2 r3
r4 . . .
r
r2
r3
r4
r(1-r)
1-r
r2(1-r)
1 + r + r2 + r3 + r4 … =
Si 0<r<1
1
1 r
m


r
rr )1( 
 2
2
)1(
r
rr 
 ...

13. 1 + r + r2 + r3 + r4 …La Serie Geométrica
si |r|<1
Si partimos de la suma de una progresión geométrica
de razón r
1
1
1
...1 12



 
rsi
r
r
rrrS
n
n
n
El valor de la serie geométrica será:
1 + r + r 2 + r 3 + r 4 … =
r
rn
n 

 1
1
lim
Este límite existe cuando -1<r<1, es decir,
Así pues: 1 + r + r2 + r3 + r4 … =
si |r|<1

14. 





 ...
10
1
10
1
10
1
1
10
3
...
10
3
10
3
10
3
2232
3
1
9
10
10
3
10/9
1
10
3
10/9
1
10
3
10/11
1
10
3





























1 3
1
10
3
...3333.0
n
n
De manera totalmente análoga, podemos probar lo obtenido
de manera geométrica:




1
1
2
1
n
n y 



1 3
1
4
1
n
n

15. La Serie Armónica:
...
5
1
4
1
3
1
2
1
1
1
1


n n
Si consideramos la siguiente sucesión de sumas parciales (finitas)
16
1
...
9
1
8
1
...
5
1
4
1
3
1
2
1
116 S
8
1
...
5
1
4
1
3
1
2
1
18 S
2
1
12 S
4
1
3
1
2
1
14 S
2
2
1
4
1
4
1
2
1
1 
2
3
1
8
1
...
8
1
2
2
1 
2
4
1
16
1
...
16
1
2
3
1 


n
n
Slim Y por lo tanto la Serie Armónica
es DIVERGENTE

16. El Criterio de Comparación
Sea con para toda n,
a) Si converge y para toda n, entonces converge
b) Si y para toda n, entonces


1n
na 0na


1n
na 

1n
nbnn ab 


1n
na 

1n
nbnn ab 
Ejemplos:
Converge, pues y converge.
Diverge, pues y la serie diverge.


1 2
)cos(
n
n
n
nn
n
2
1
2
)cos(
 

1 2
1
n
n


1
1
n n nn
11
 

1
1
n n

17. Calculando, numéricamente el valor de una Serie
La Serie Geométrica
La Serie Armónica
La Serie del recíproco de los cuadrados de los naturales
Una serie Alternante

18. Cuando analizamos la Serie Geométrica
Series de Potencias


0n
n
x
Encontramos que esta converge a 1/(1-x) en el intervalo (-1, 1),
es decir, si consideramos a la función




0
)(
n
n
xxf
Su dominio será precisamente el intervalo (-1, 1) ya que ahí es
donde la serie converge y por lo tanto f (x) está definida.
Diremos entonces que la serie de potencias representa a la
función 1/(1-x) en el intervalo (-1, 1)

19. ...1
1
1 432


xxxx
x
A partir de la Serie Geométrica podemos generar otras series de
potencias y series numéricas importantes: Ver Applet
Cambiamos x por -x
...1
1
1 432


xxxx
x Antiderivando en ambos lados
...
5432
)1ln(
5432

xxxx
xx
Sustituyendo x =1, obtenemos:
...
5
1
4
1
3
1
2
1
12ln  Ver Applet
n
n
n
x
n






1
1
)1(






1
1
)1(
n
n
n
Ver Applet

20. ...1
1
1 432


xxxx
x
Procedamos ahora de la siguiente manera:
Cambiamos x por -x
...1
1
1 432


xxxx
x
Antiderivando en ambos lados
Sustituyendo x =1,
Ver Applet
Cambiamos x por 2
x
...1
1
1 8642
2


xxxx
x
...
9753
arctan
9753

xxxx
xx
...
9
1
7
1
5
1
3
1
11arctan
4


...
9
4
7
4
5
4
3
4
4 








1
12
1
12
)1(
n
n
n
x
n







1
1
12
)1(
n
n
n

21. El Teorema de Taylor con residuo, también nos proporciona
interesantes series de potencias. Por ejemplo del desarrollo de
Taylor para la función exponencial:
n
n
x
E
n
xxx
xe 
!
...
!3!2
1
32
0
Tendremos una representación en serie de potencias
...
!3!2
1
32

xx
xex




0
!n
n
x
n
x
e
...
!7!5!3
753

xxx
xsenx 






1
121
!)12(
)1(
n
nn
n
x
senx
Análogamente podemos representar en serie de potencias a la
función seno
Ver Applet
Ver Applet

22. En los cursos de Cálculo Integral se menciona que la función
no tiene una antiderivada representable por medio
de un número finito de funciones “conocidas”
En nuestros términos, podemos preguntarnos por la solución de:
2
)( x
exf 

2
x
e
dx
dy 
 ...
!3!2
1
64
2

xx
x
Antiderivando en ambos términos, obtenemos:
Con y(0) = 0
...
)!3(7)!2(53
)(
753

xxx
xxy
Así pues la solución de la ecuación planteada se representa por
medio de una serie de potencias.
Ver Applet
Ver Applet

23. Muchas Gracias