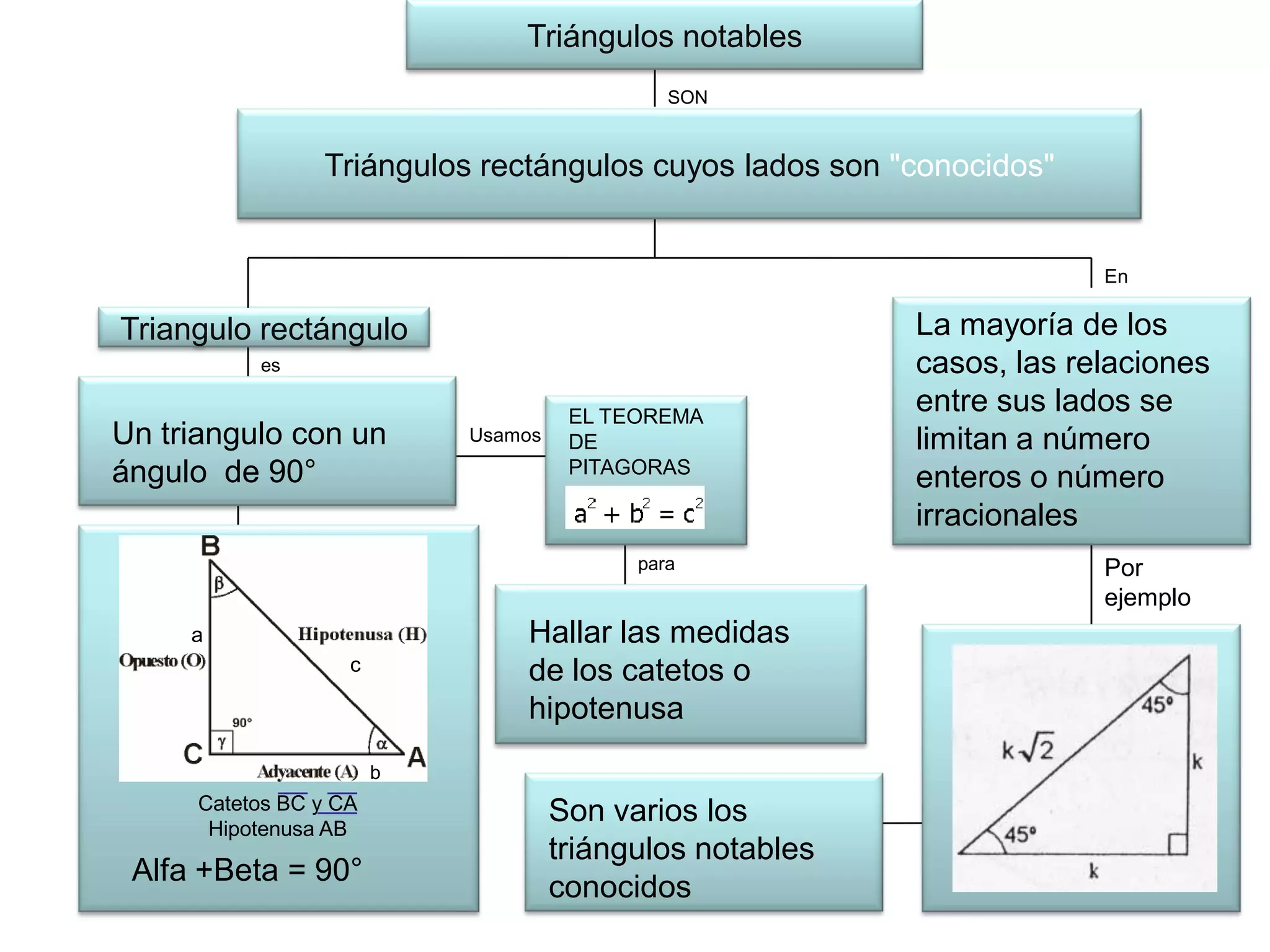
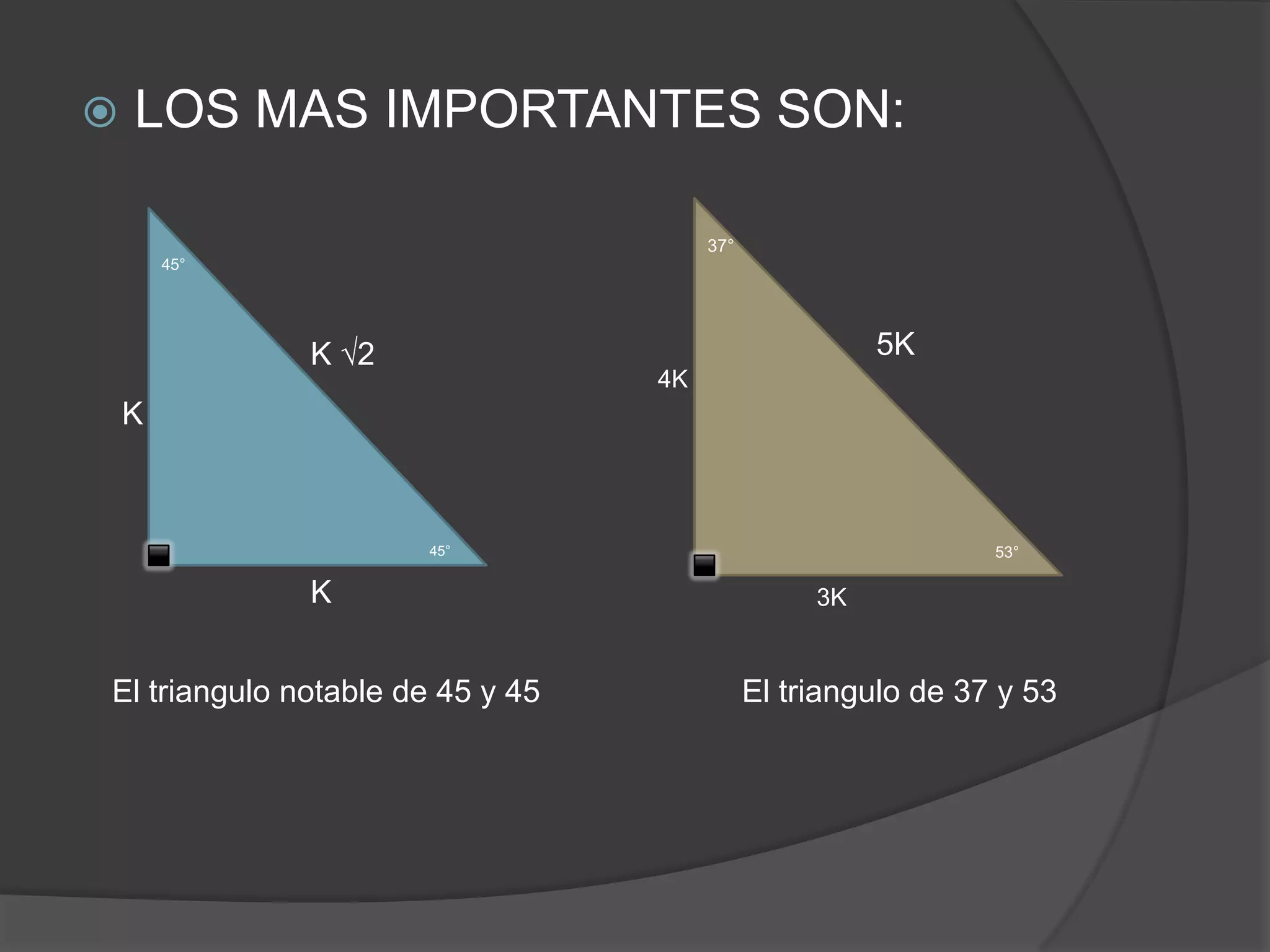
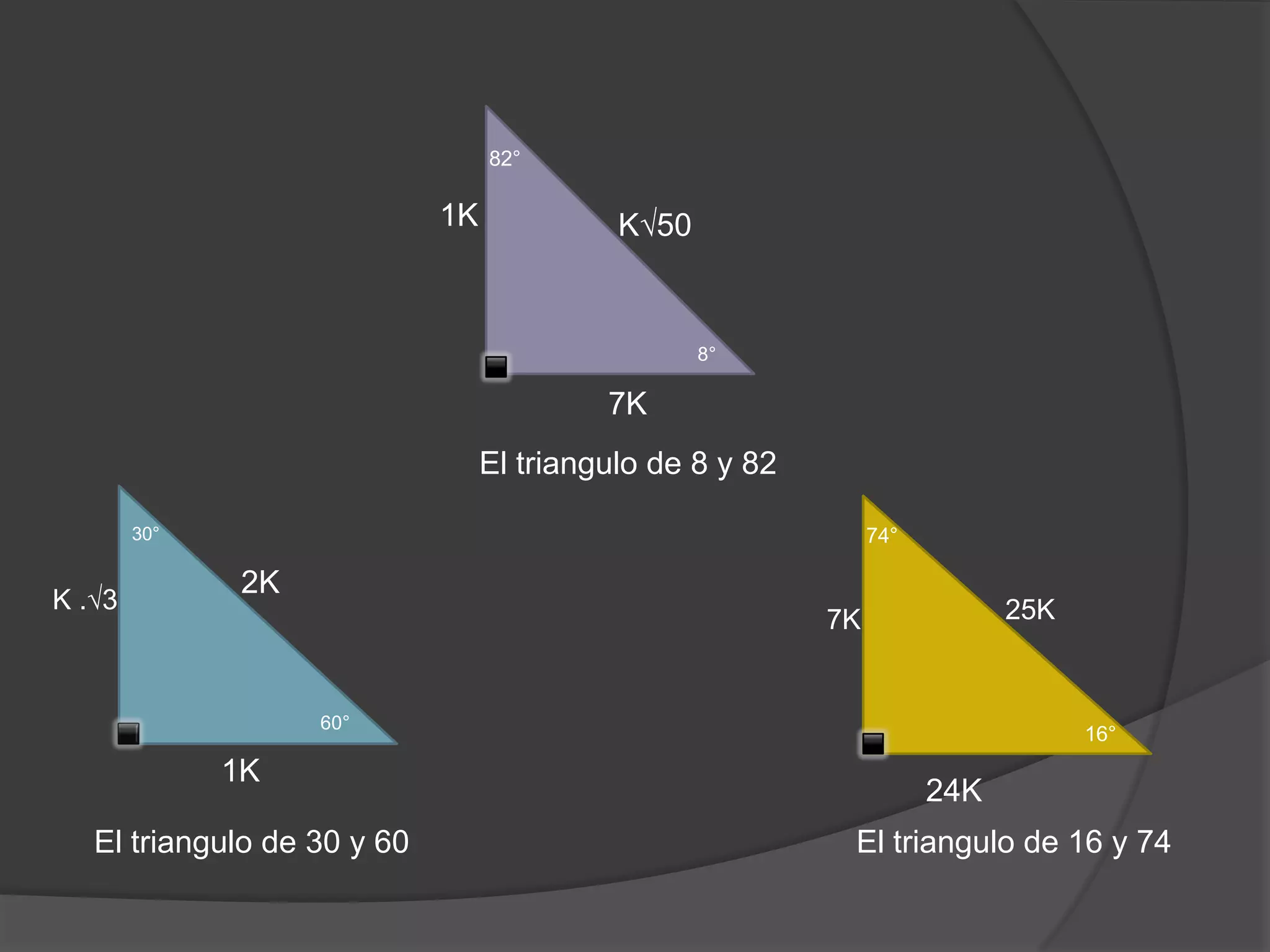
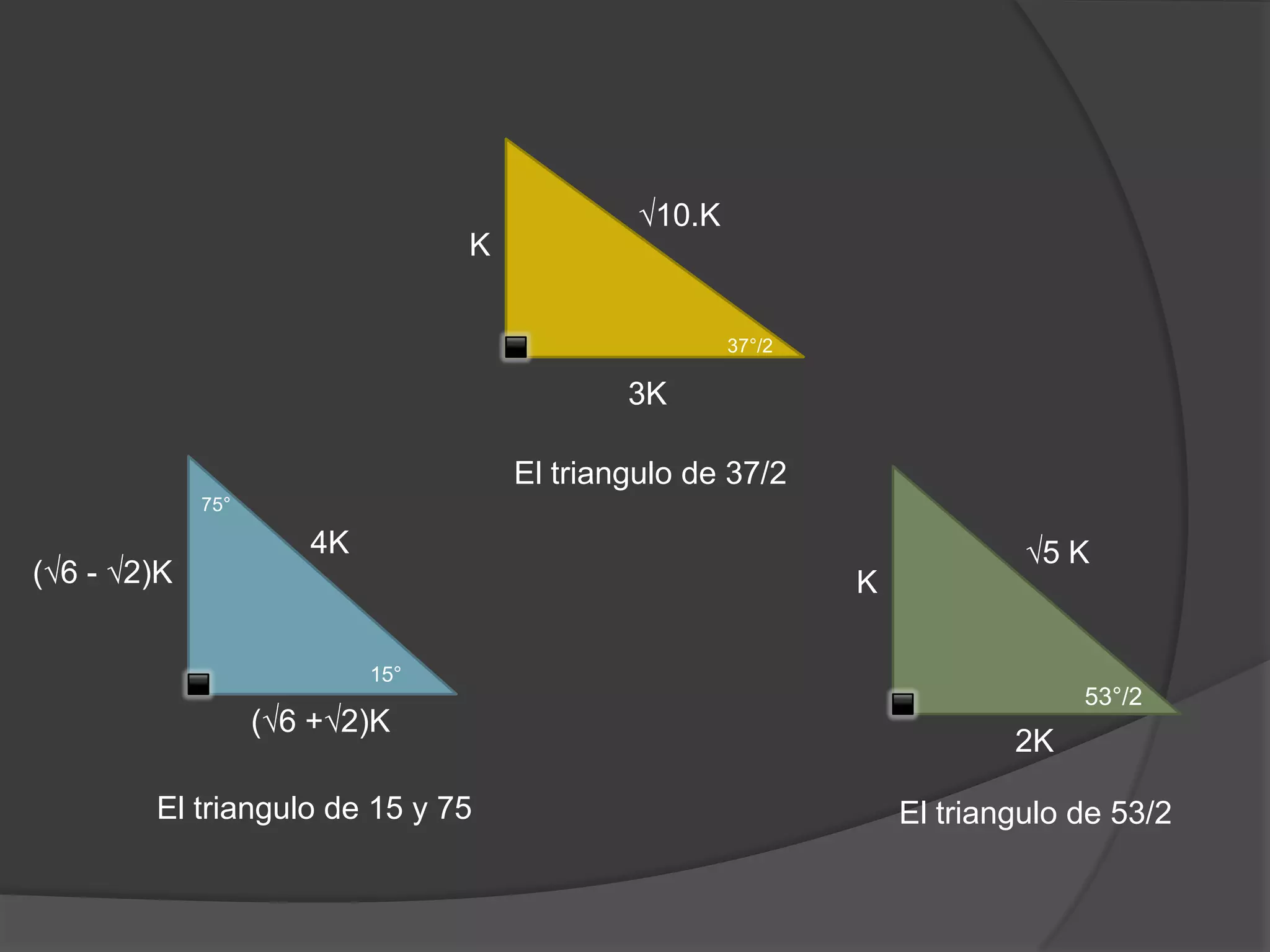
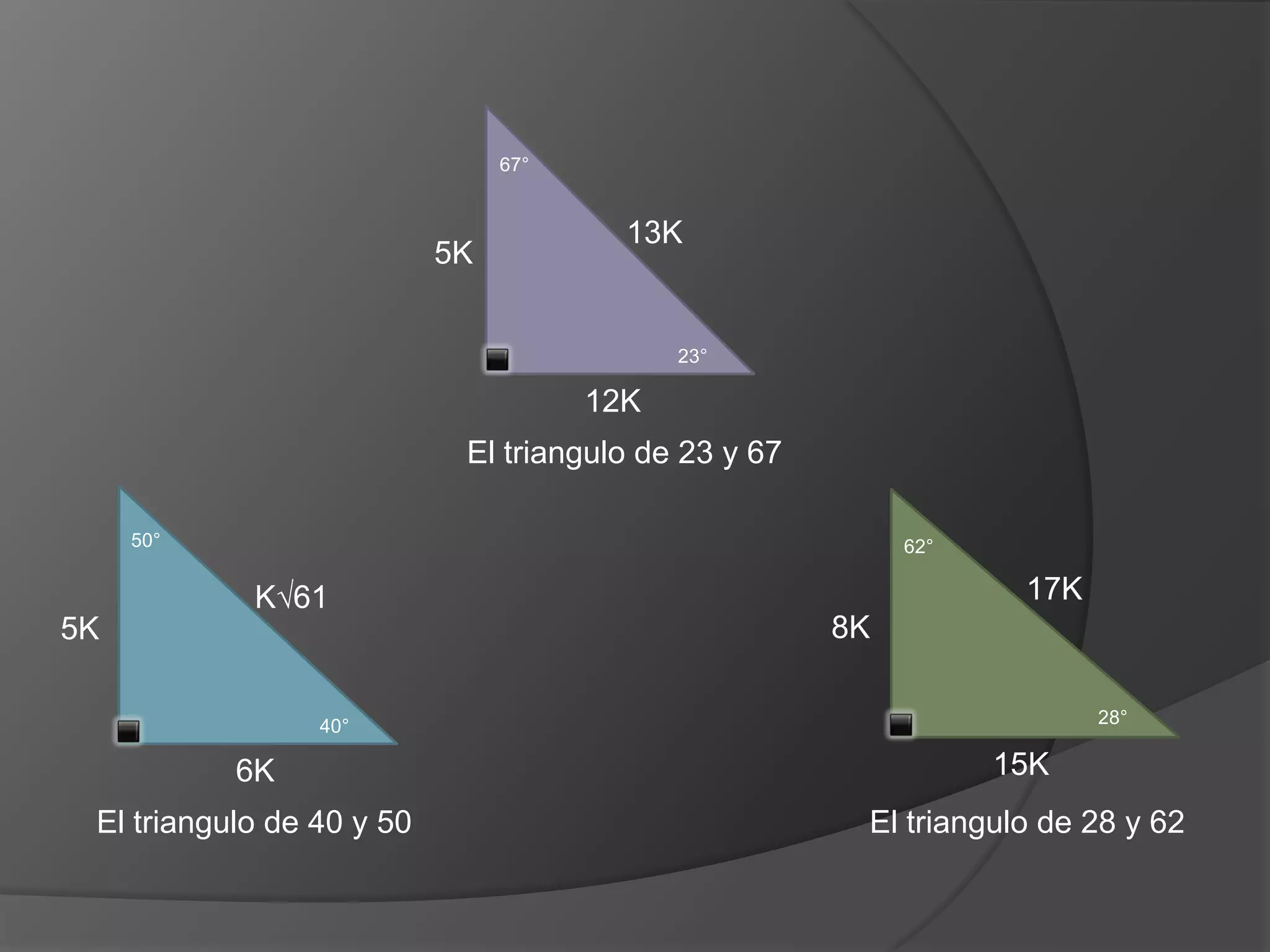
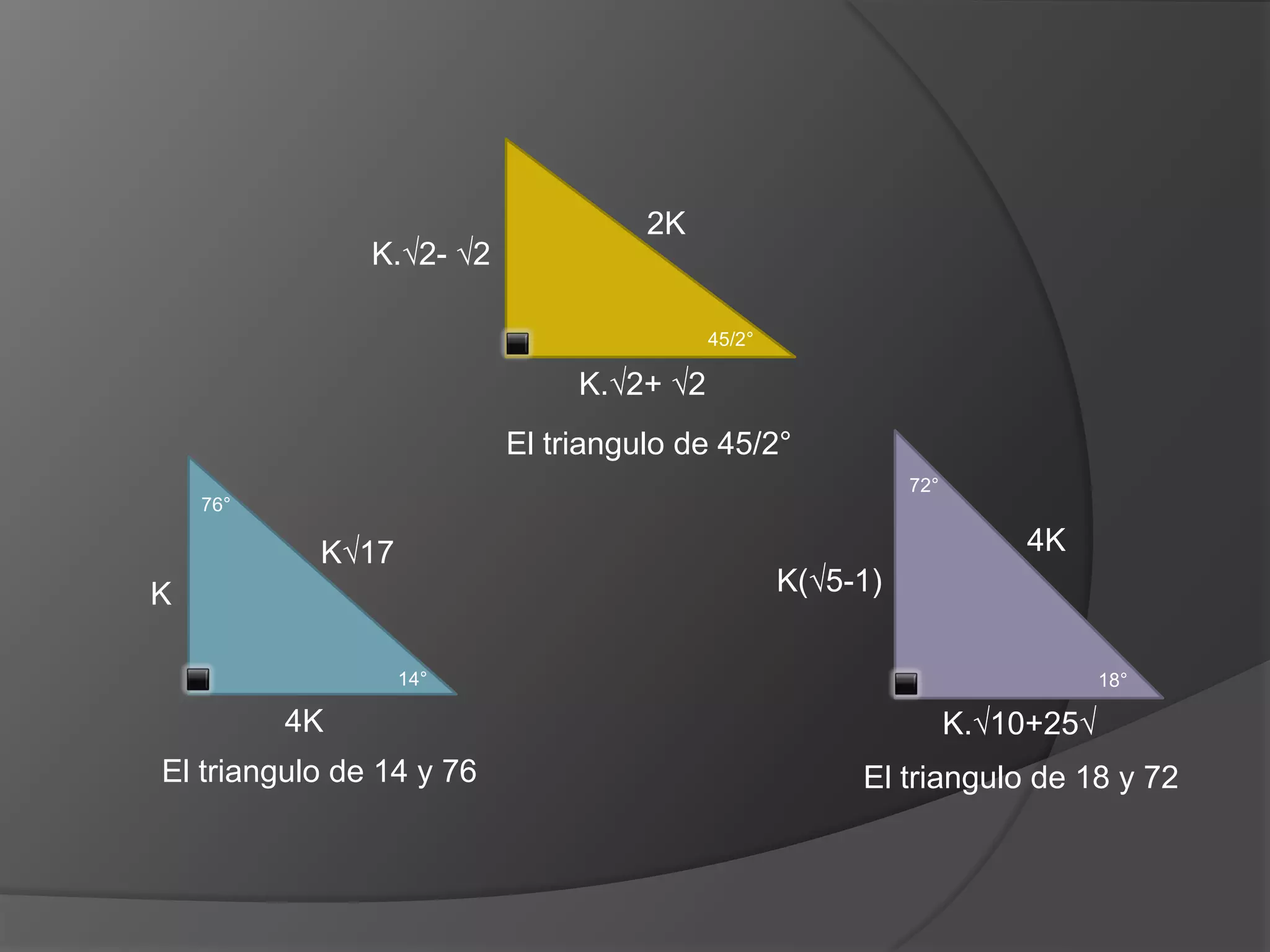
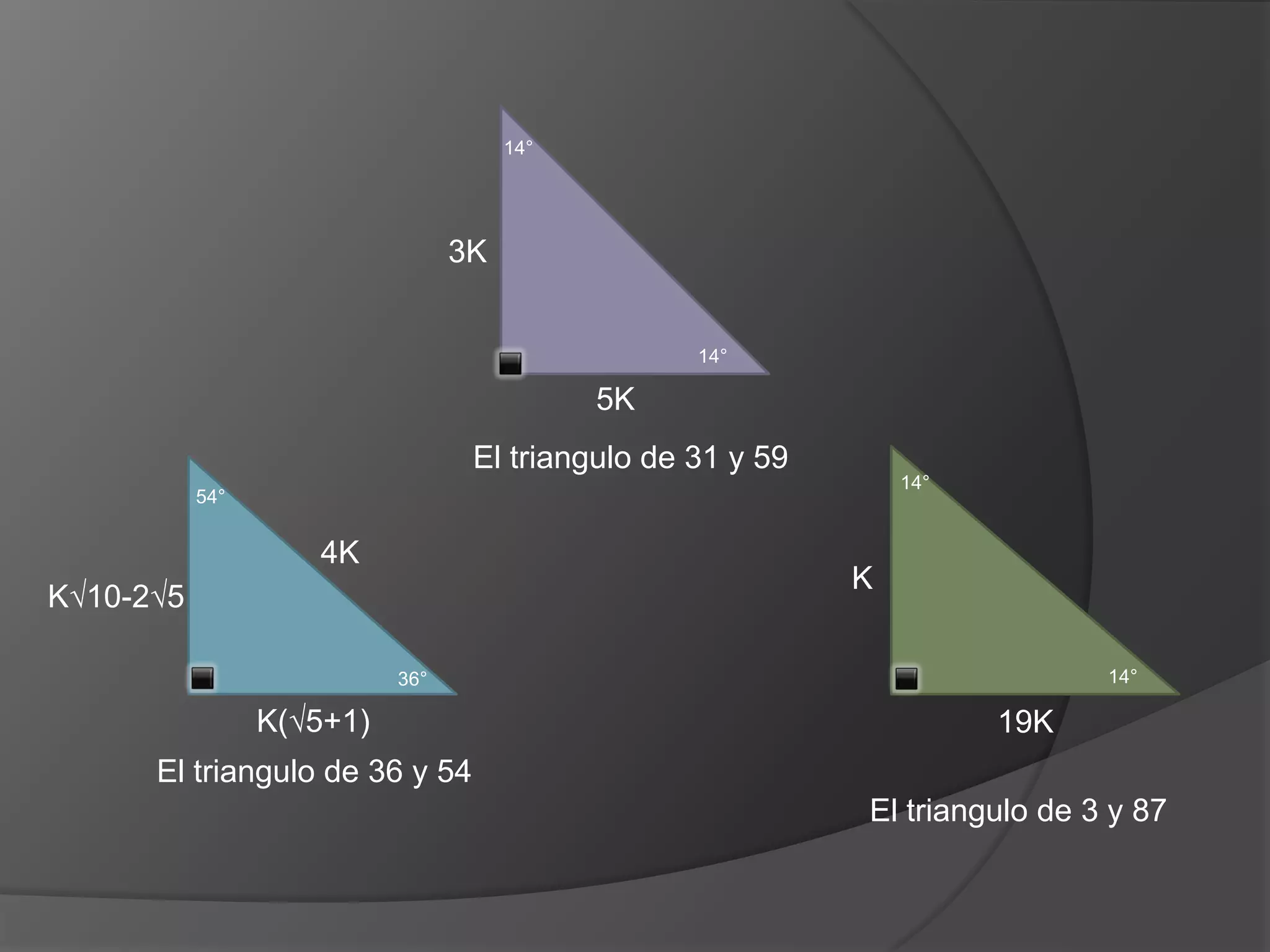
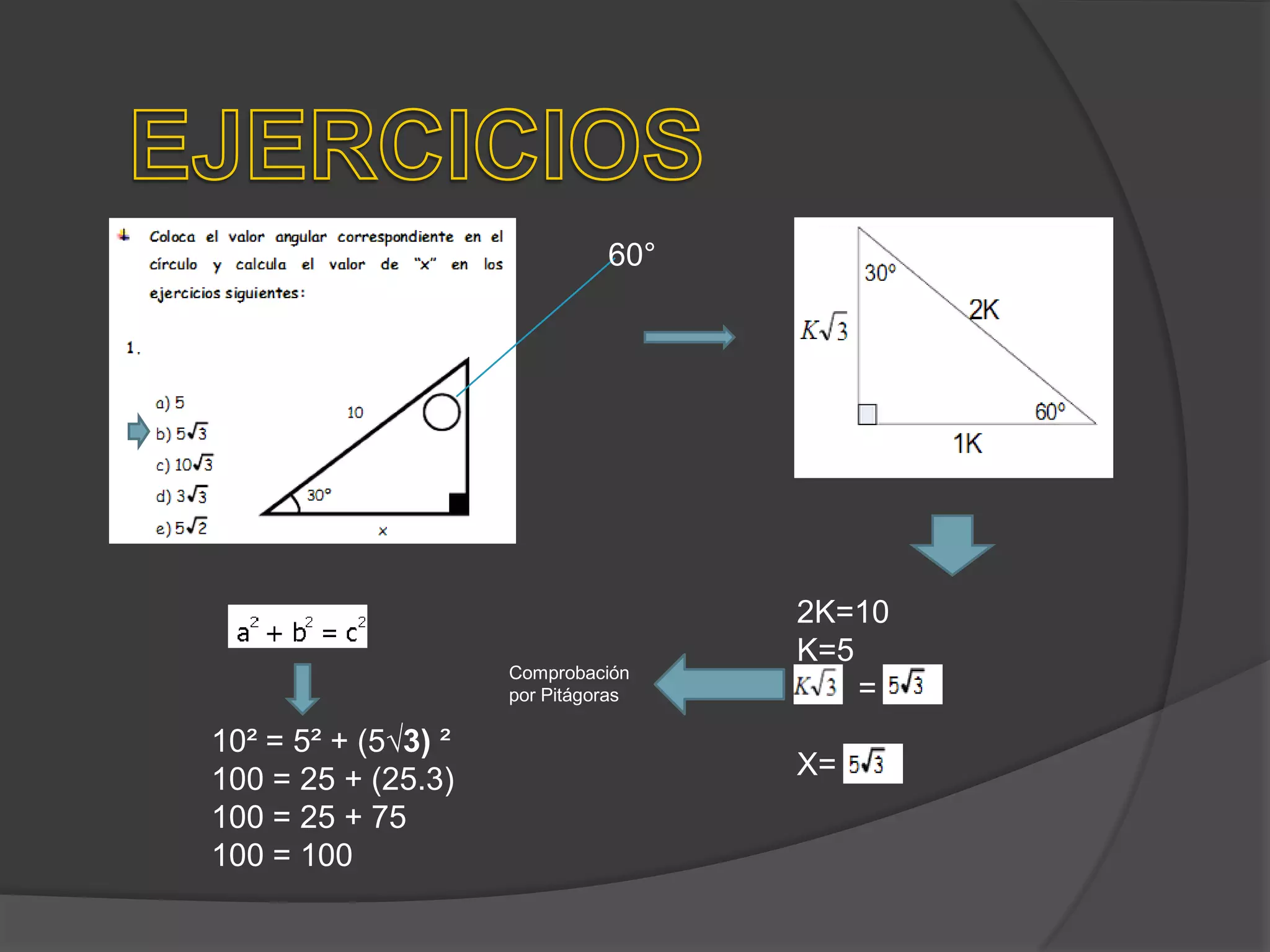
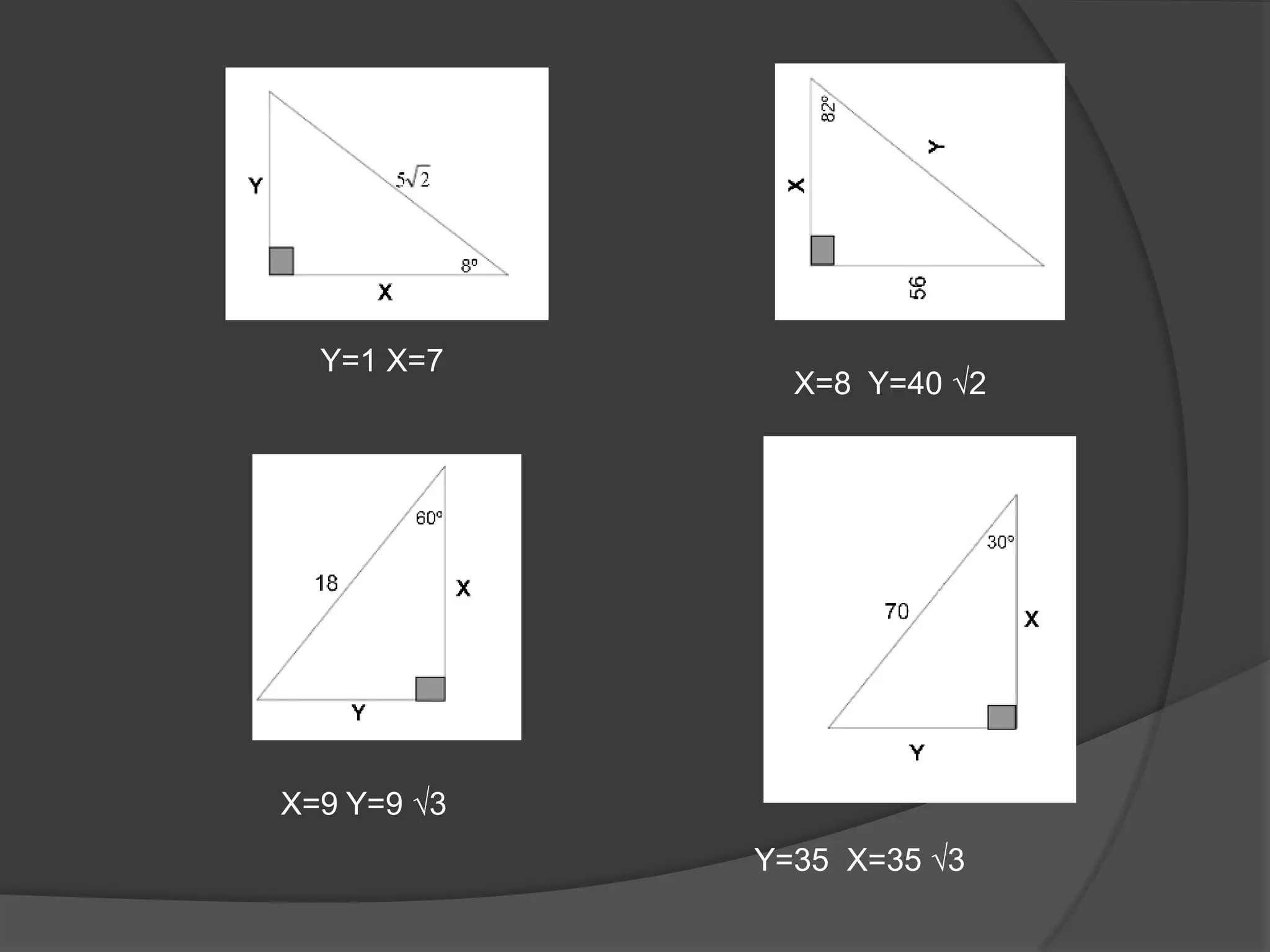
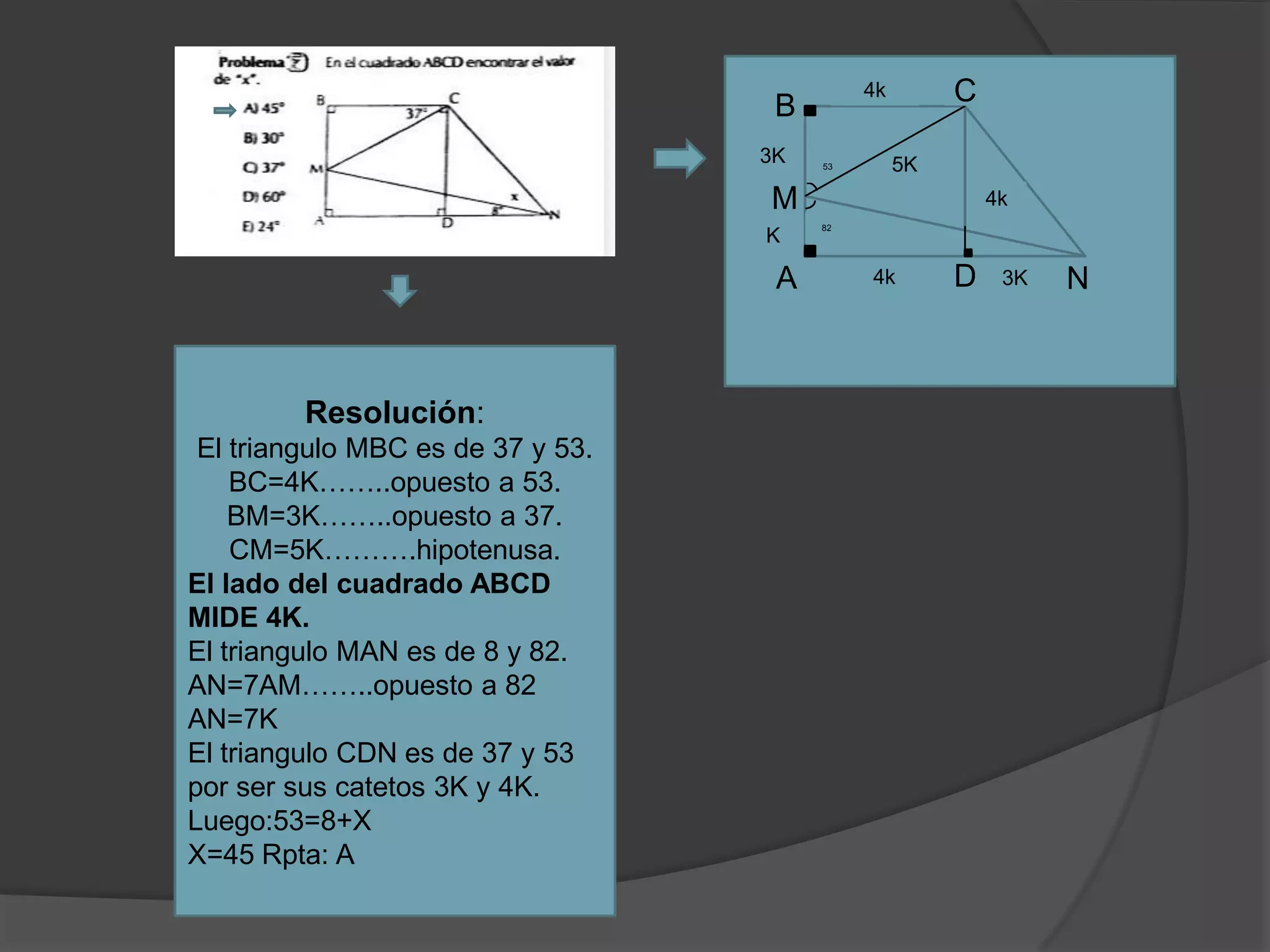
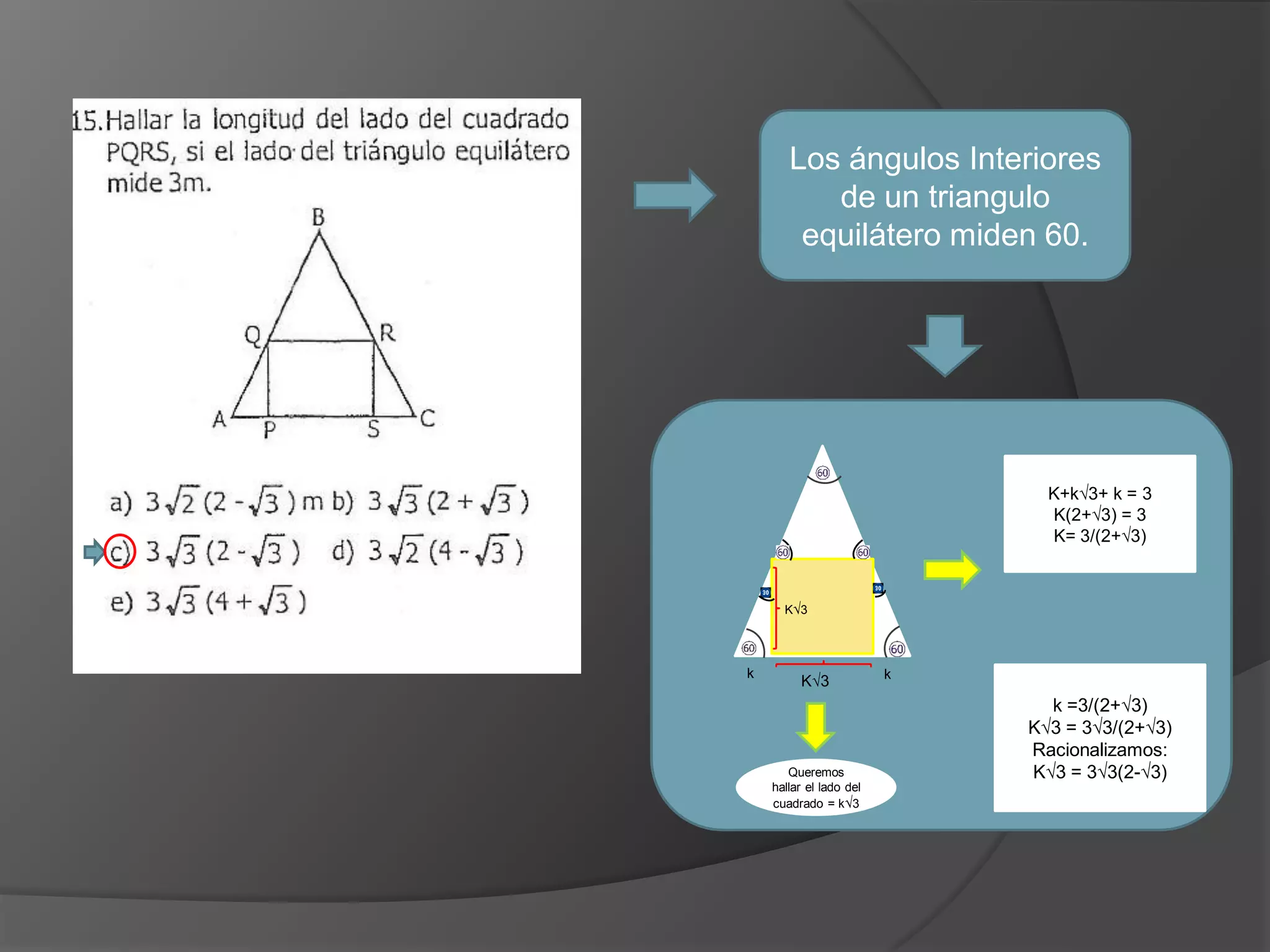
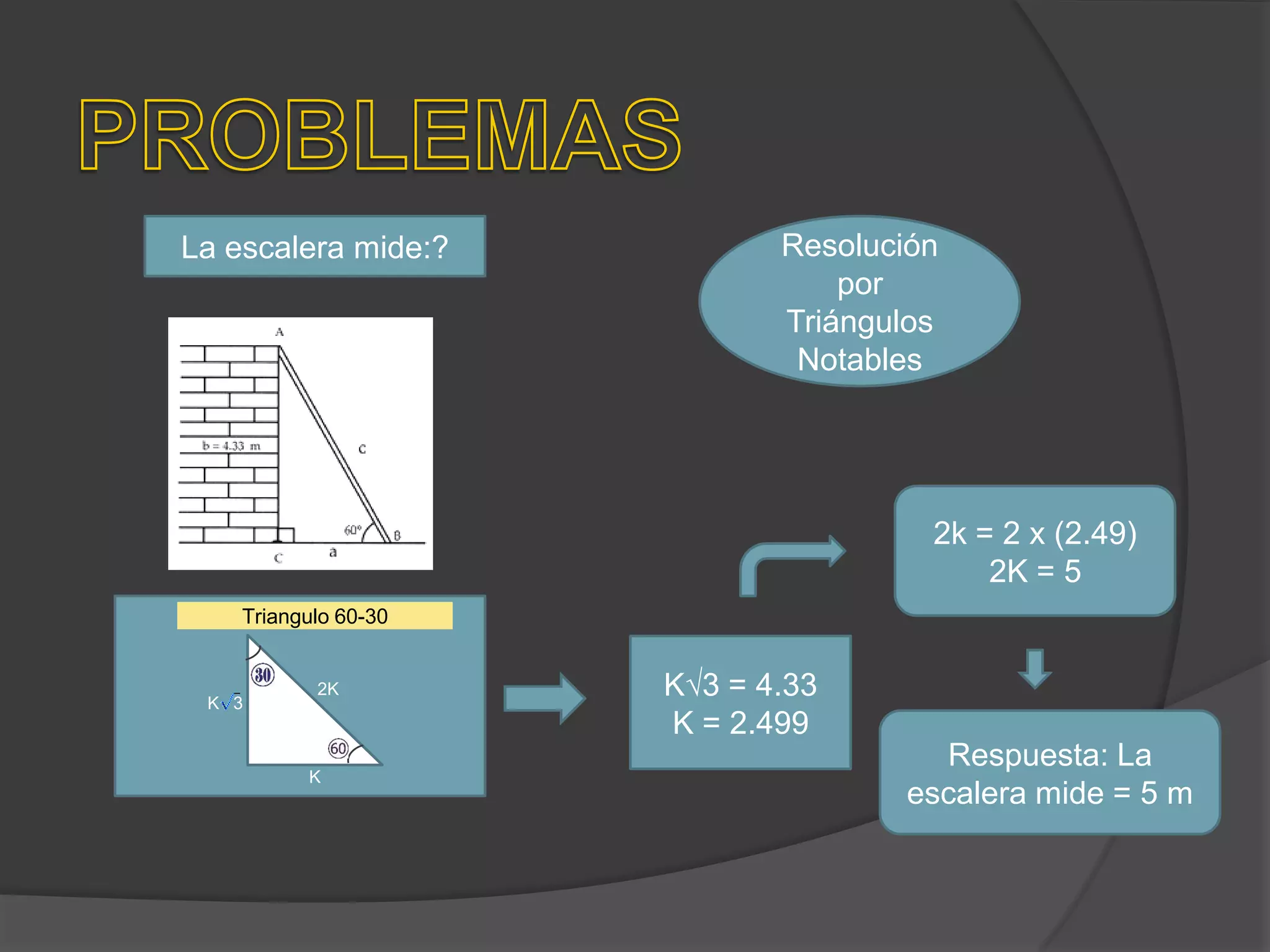
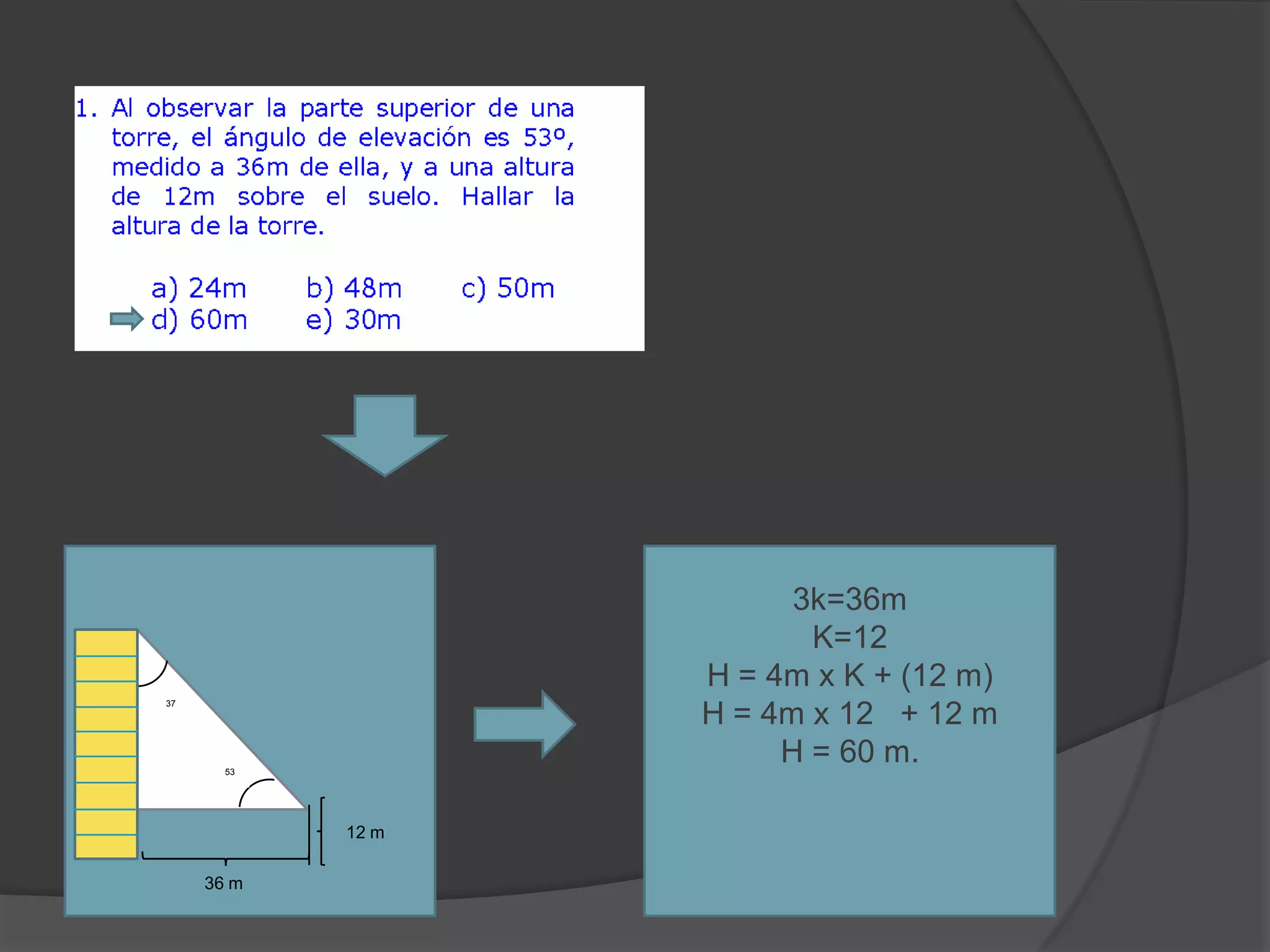
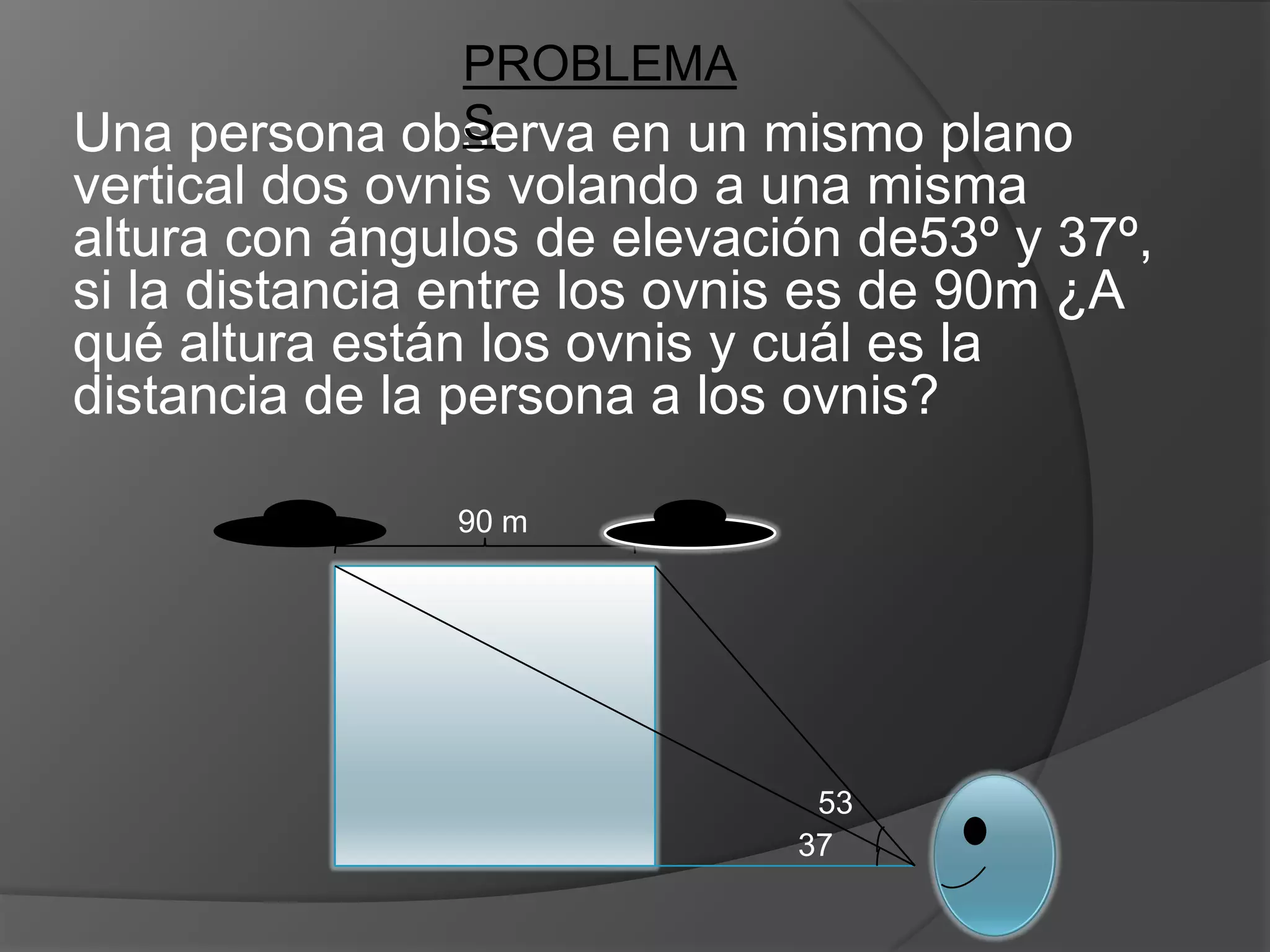
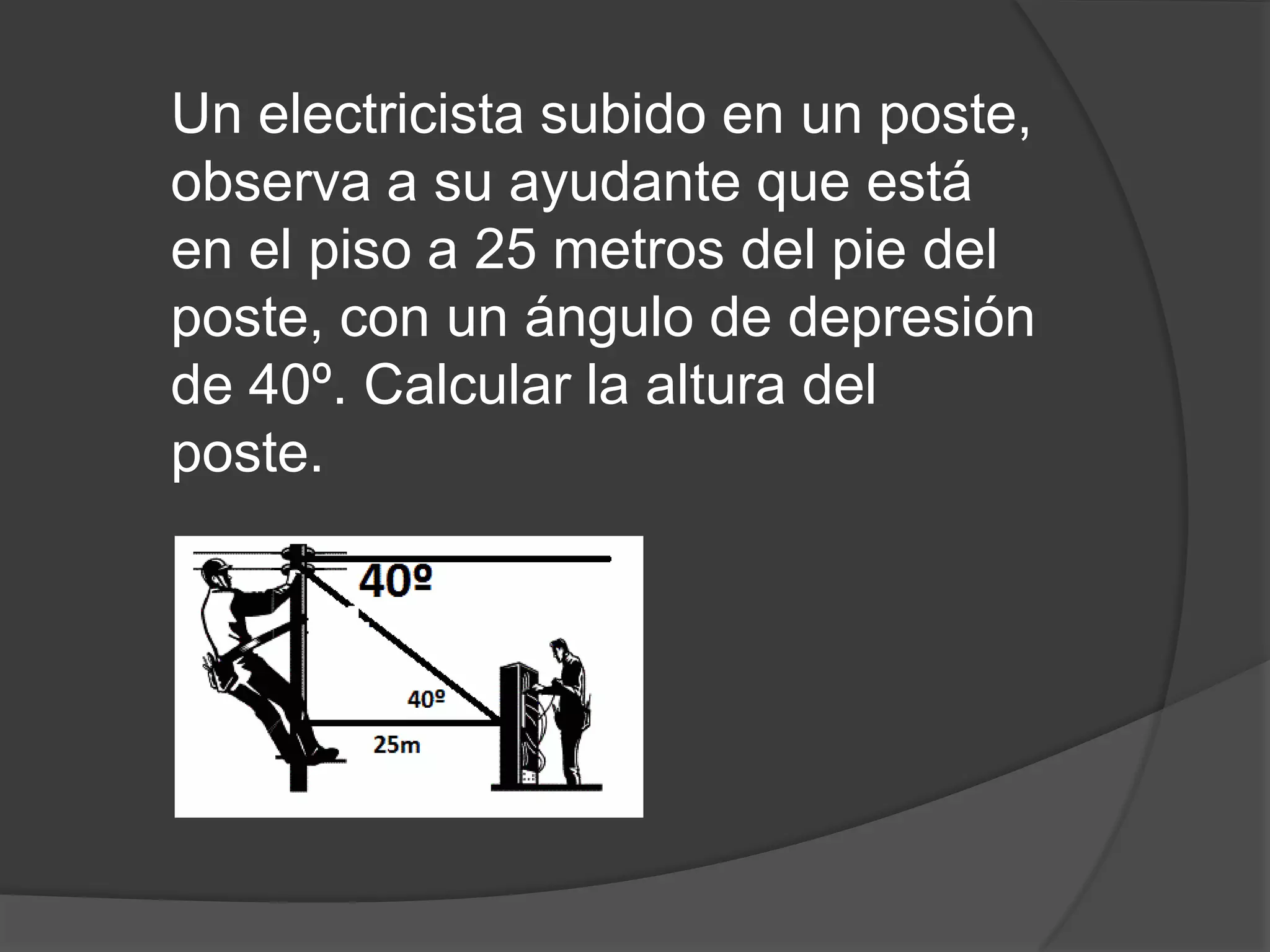
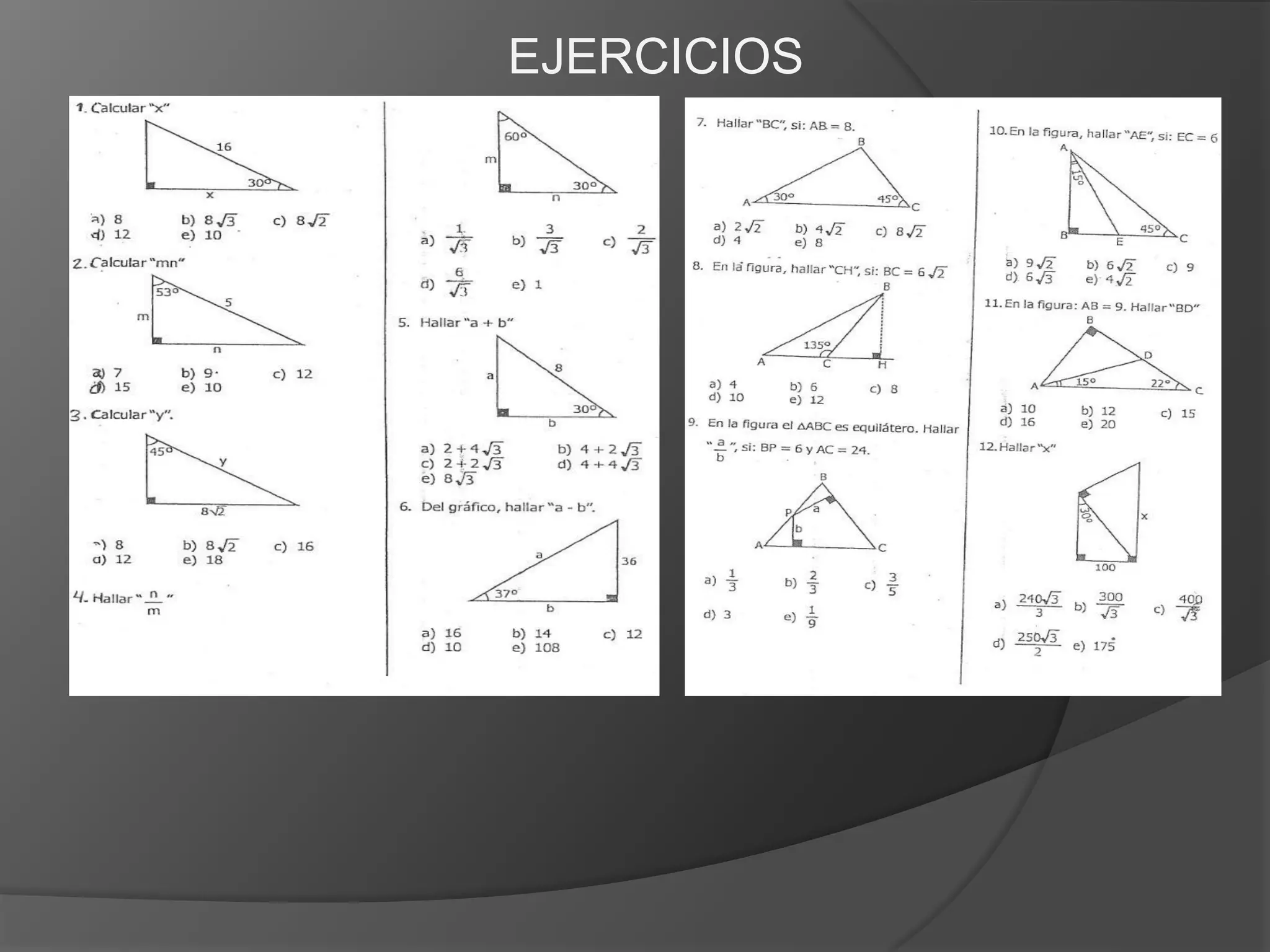
Este documento presenta información sobre triángulos notables. Explica que los triángulos notables son triángulos rectángulos cuyos lados tienen relaciones de números enteros o irracionales. Describe varios triángulos notables comunes como el triángulo de 45-45 y el triángulo de 30-60. Incluye ejemplos de cómo usar los triángulos notables para resolver problemas.

1. TRIÁNGULOS NOTABLES
DATOS INFORMATIVOS:
I.E.:
Manuel Muñoz Najar
Realizado por:
Marco Fraquet
Javier Valenzuela
Tema:
Triángulos Notables
Profesora
Doris Gutiérrez Pacheco

3. ORGANIZADOR
VISUAL DE
TRIANGULOS
NOTABLES

4. Triángulos notables
SON
Triángulos rectángulos cuyos lados son "conocidos"
En
Triangulo rectángulo
es
Un triangulo con un
ángulo de 90°
Usamos
EL TEOREMA
DE
PITAGORAS
para
Hallar las medidas
de los catetos o
hipotenusa
a
c
b
Catetos BC y CA
Hipotenusa AB
Alfa +Beta = 90°
Son varios los
triángulos notables
conocidos
La mayoría de los
casos, las relaciones
entre sus lados se
limitan a número
enteros o número
irracionales
Por
ejemplo

6. Son aquellos triángulos que a partir
de la razón de dos de sus lados se
pueden calcular su tercer lado y la
medida de sus ángulos internos

7. Funciones Trigonométricas
En un triángulo rectángulo, las razones trigonométricas del ángulo alfa
; con vértice en A, son:
 El seno: la razón entre el cateto opuesto y la hipotenusa.


El coseno: la razón entre el cateto adyacente y la hipotenusa.
La tangente: la razón entre el cateto opuesto y el adyacente.

8. 
LOS MAS IMPORTANTES SON:
37°
45°
5K
K √2
4K
K
45°
K
El triangulo notable de 45 y 45
53°
3K
El triangulo de 37 y 53

9. 82°
1K
K√50
8°
7K
El triangulo de 8 y 82
30°
K .√3
74°
2K
25K
7K
60°
1K
El triangulo de 30 y 60
16°
24K
El triangulo de 16 y 74

10. √10.K
K
37°/2
3K
El triangulo de 37/2
75°
(√6 - √2)K
4K
√5 K
K
15°
(√6 +√2)K
El triangulo de 15 y 75
53°/2
2K
El triangulo de 53/2

11. 67°
5K
13K
23°
12K
El triangulo de 23 y 67
50°
62°
17K
K√61
8K
5K
28°
40°
6K
15K
El triangulo de 40 y 50
El triangulo de 28 y 62

12. K.√2- √2
2K
45/2°
K.√2+ √2
El triangulo de 45/2°
72°
76°
4K
K√17
K(√5-1)
K
14°
4K
El triangulo de 14 y 76
18°
K.√10+25√
El triangulo de 18 y 72

13. 14°
3K
14°
5K
El triangulo de 31 y 59
14°
54°
4K
K
K√10-2√5
14°
36°
K(√5+1)
19K
El triangulo de 36 y 54
El triangulo de 3 y 87

15. 60°
Comprobación
por Pitágoras
10² = 5² + (5√3) ²
100 = 25 + (25.3)
100 = 25 + 75
100 = 100
2K=10
K=5
=
X=

16. 3
2
Y=1 X=7
X=8 Y=40 √2
5
4
X=9 Y=9 √3
Y=35 X=35 √3

17. 3K
C
4k
B
53
5K
M
K
A
Resolución:
El triangulo MBC es de 37 y 53.
BC=4K……..opuesto a 53.
BM=3K……..opuesto a 37.
CM=5K……….hipotenusa.
El lado del cuadrado ABCD
MIDE 4K.
El triangulo MAN es de 8 y 82.
AN=7AM……..opuesto a 82
AN=7K
El triangulo CDN es de 37 y 53
por ser sus catetos 3K y 4K.
Luego:53=8+X
X=45 Rpta: A
4k
82
4k
D
3K
N

18. Los ángulos Interiores
de un triangulo
equilátero miden 60.
K+k√3+ k = 3
K(2+√3) = 3
K= 3/(2+√3)
K√3
k
K√3
Queremos
hallar el lado del
cuadrado = k√3
k
k =3/(2+√3)
K√3 = 3√3/(2+√3)
Racionalizamos:
K√3 = 3√3(2-√3)

19. La escalera mide:?
Resolución
por
Triángulos
Notables
2k = 2 x (2.49)
2K = 5
Triangulo 60-30
K 3
2K
K
K√3 = 4.33
K = 2.499
Respuesta: La
escalera mide = 5 m

20. 3k=36m
K=12
H = 4m x K + (12 m)
H = 4m x 12 + 12 m
H = 60 m.
37
53
12 m
36 m

21. PROBLEMA
S
Una persona observa en un mismo plano
vertical dos ovnis volando a una misma
altura con ángulos de elevación de53º y 37º,
si la distancia entre los ovnis es de 90m ¿A
qué altura están los ovnis y cuál es la
distancia de la persona a los ovnis?
90 m
53
37

22. Un electricista subido en un poste,
observa a su ayudante que está
en el piso a 25 metros del pie del
poste, con un ángulo de depresión
de 40º. Calcular la altura del
poste.

23. Un navegante ubica su barco a 50 m del
pie de un faro y observa la torre de éste
con un ángulo de elevación de 53°.¿Cual
es la altura del faro?.
37°
50M

25. EJERCICIOS

26. 






http://cptodostrigo.blogspot.com/2011/05/triangulos-notables.htm
http://matematica.pe/triangulos-notables-ejercicios-resueltos-quintode-secundaria-pdf/
http://www.ditutor.com/geometria/triangulo_rectangulo.html
http://es.scribd.com/doc/19770751/Triangulos-Notables
http://matematica.pe/triangulos-rectangulos-notables-ejerciciosresueltos-cuarto-de-secundaria-pdf/
http://profe-alexz.blogspot.com/2011/05/triangulos-rectangulosnotables.html
http://es.scribd.com/doc/15267686/Triangulos-Notables