8. analysis of truss part ii, method of section, by-ghumare s m
•
5 recomendaciones•1,846 vistas
Analysis of Truss-Method of Section
Denunciar
Compartir
Denunciar
Compartir
Descargar para leer sin conexión
Recomendados
Recomendados
Más contenido relacionado
La actualidad más candente
La actualidad más candente (20)
Solution Manual for Structural Analysis 6th SI by Aslam Kassimali

Solution Manual for Structural Analysis 6th SI by Aslam Kassimali
Approximate Analysis of Statically Indeteminate Structures.pdf

Approximate Analysis of Statically Indeteminate Structures.pdf
Lec.2 statically determinate structures & statically indeterminate struct...

Lec.2 statically determinate structures & statically indeterminate struct...
Structure analysis assignment 7 determinate frame analysis

Structure analysis assignment 7 determinate frame analysis
Structure Design-I ( Analysis of truss by method of joint.)

Structure Design-I ( Analysis of truss by method of joint.)
7. analysis of truss part i, methof of joint, by-ghumare s m

7. analysis of truss part i, methof of joint, by-ghumare s m
Solution of Chapter- 05 - stresses in beam - Strength of Materials by Singer

Solution of Chapter- 05 - stresses in beam - Strength of Materials by Singer
Structural Analysis (Solutions) Chapter 9 by Wajahat

Structural Analysis (Solutions) Chapter 9 by Wajahat
Similar a 8. analysis of truss part ii, method of section, by-ghumare s m
Similar a 8. analysis of truss part ii, method of section, by-ghumare s m (20)
solution-manual-3rd-ed-metal-forming-mechanics-and-metallurgy-chapter-1-3

solution-manual-3rd-ed-metal-forming-mechanics-and-metallurgy-chapter-1-3
MEC_803_Part_2-Two_Dimensional_Problems_in_Cartesian_Coordinate_System-2.pdf

MEC_803_Part_2-Two_Dimensional_Problems_in_Cartesian_Coordinate_System-2.pdf
Formul me-3074683 Erdi Karaçal Mechanical Engineer University of Gaziantep

Formul me-3074683 Erdi Karaçal Mechanical Engineer University of Gaziantep
Más de smghumare
Más de smghumare (17)
Solid Mechanics Direct & Bending Strssess at Corners.pptx

Solid Mechanics Direct & Bending Strssess at Corners.pptx
Solid Mechanics Numerical on Direct and Bending Strssess.pptx

Solid Mechanics Numerical on Direct and Bending Strssess.pptx
Solid Mechanics Numerical on Euler's Theory-II.pptx

Solid Mechanics Numerical on Euler's Theory-II.pptx
Solid Mechanics Numericals on Euler's Theory-I.pptx

Solid Mechanics Numericals on Euler's Theory-I.pptx
Solid Mechanics -Introduction to Column Theory.pptx

Solid Mechanics -Introduction to Column Theory.pptx
Último
Top Rated Pune Call Girls Budhwar Peth ⟟ 6297143586 ⟟ Call Me For Genuine Sex Service At Affordable Rate
Booking Contact Details
WhatsApp Chat: +91-6297143586
pune Escort Service includes providing maximum physical satisfaction to their clients as well as engaging conversation that keeps your time enjoyable and entertaining. Plus they look fabulously elegant; making an impressionable.
Independent Escorts pune understands the value of confidentiality and discretion - they will go the extra mile to meet your needs. Simply contact them via text messaging or through their online profiles; they'd be more than delighted to accommodate any request or arrange a romantic date or fun-filled night together.
We provide -
01-may-2024(v.n)
Top Rated Pune Call Girls Budhwar Peth ⟟ 6297143586 ⟟ Call Me For Genuine Se...

Top Rated Pune Call Girls Budhwar Peth ⟟ 6297143586 ⟟ Call Me For Genuine Se...Call Girls in Nagpur High Profile
Call girls in delhi ✔️✔️🔝 9953056974 🔝✔️✔️Welcome To Vip Escort Services In Delhi [ ]Noida Gurgaon 24/7 Open Sex Escort Services With Happy Ending ServiCe Done By Most Attractive Charming Soft Spoken Bold Beautiful Full Cooperative Independent Escort Girls ServiCe In All-Star Hotel And Home Service In All Over Delhi, Noida, Gurgaon, Faridabad, Ghaziabad, Greater Noida,
• IN CALL AND OUT CALL SERVICE IN DELHI NCR
• 3* 5* 7* HOTELS SERVICE IN DELHI NCR
• 24 HOURS AVAILABLE IN DELHI NCR
• INDIAN, RUSSIAN, PUNJABI, KASHMIRI ESCORTS
• REAL MODELS, COLLEGE GIRLS, HOUSE WIFE, ALSO AVAILABLE
• SHORT TIME AND FULL TIME SERVICE AVAILABLE
• HYGIENIC FULL AC NEAT AND CLEAN ROOMS AVAIL. IN HOTEL 24 HOURS
• DAILY NEW ESCORTS STAFF AVAILABLE
• MINIMUM TO MAXIMUM RANGE AVAILABLE.
Call Girls in Delhi & Independent Escort Service –
CALL GIRLS SERVICE DELHI NCR
Vip call girls in Delhi
Call Girls in Delhi, Call Girl Service 24×7 open
Call Girls in Delhi Best Delhi Escorts in Delhi
Low Rate Call Girls In Saket Delhi
X~CALL GIRLS IN Ramesh Nagar Metro
best Delhi call girls and Delhi escort service.
CALL GIRLS SERVICE IN ALL DELHI …
(Delhi) Call Girls in (Chanakyapuri)
Hot And Sexy Independent Model Escort Service In Delhi Unlimited Enjoy Genuine 100% Profiles And Trusted Door Step Call Girls Feel Free To Call Us Female Service Hot Busty & Sexy Party Girls Available For Complete Enjoyment. We Guarantee Full Satisfaction & In Case Of Any Unhappy Experience, We Would Refund Your Fees, Without Any Questions Asked. Feel Free To Call Us Female Service Provider Hours Opens Thanks.
Delhi Escorts Services 100% secure Services.Incall_OutCall Available and outcall Services provide.
We are available 24*7 for Full Night and short Time Escort Services all over Delhi NCR.
Delhi All Hotel Services available 3* 4* 5* Call Call
Delhi Escorts Services And Delhi Call Girl Agency 100% secure Services in my agency. Incall and outcall Services provide.
We are available 24*7 for Full Night and short Time Escort Services my agency in all over New Delhi
Delhi All Hotel Services available my agency
SERVICES [✓✓✓]
Housewife
College Girl
VIP Escort
Independent Girl
Aunty
Without a Condom sucking )?
Sexy Aunty.DSL (Dick Sucking Lips)?
DT (Dining at the Toes English Spanking)
Doggie (Sex style from no behind)??
OutCall- All Over Delhi Noida Gurgaon 24/7
FOR APPOINTMENT Call/Whatsop / 9953056974Call Girls in Ramesh Nagar Delhi 💯 Call Us 🔝9953056974 🔝 Escort Service

Call Girls in Ramesh Nagar Delhi 💯 Call Us 🔝9953056974 🔝 Escort Service9953056974 Low Rate Call Girls In Saket, Delhi NCR
Call Girl Bhosari Indira Call Now: 8617697112 Bhosari Escorts Booking Contact Details WhatsApp Chat: +91-8617697112 Bhosari Escort Service includes providing maximum physical satisfaction to their clients as well as engaging conversation that keeps your time enjoyable and entertaining. Plus they look fabulously elegant; making an impressionable. Independent Escorts Bhosari understands the value of confidentiality and discretion - they will go the extra mile to meet your needs. Simply contact them via text messaging or through their online profiles; they'd be more than delighted to accommodate any request or arrange a romantic date or fun-filled night together. We provide –(INDIRA) Call Girl Bhosari Call Now 8617697112 Bhosari Escorts 24x7

(INDIRA) Call Girl Bhosari Call Now 8617697112 Bhosari Escorts 24x7Call Girls in Nagpur High Profile Call Girls
Último (20)
VIP Model Call Girls Kothrud ( Pune ) Call ON 8005736733 Starting From 5K to ...

VIP Model Call Girls Kothrud ( Pune ) Call ON 8005736733 Starting From 5K to ...
Call Girls Pimpri Chinchwad Call Me 7737669865 Budget Friendly No Advance Boo...

Call Girls Pimpri Chinchwad Call Me 7737669865 Budget Friendly No Advance Boo...
chapter 5.pptx: drainage and irrigation engineering

chapter 5.pptx: drainage and irrigation engineering
VIP Call Girls Ankleshwar 7001035870 Whatsapp Number, 24/07 Booking

VIP Call Girls Ankleshwar 7001035870 Whatsapp Number, 24/07 Booking
VIP Call Girls Palanpur 7001035870 Whatsapp Number, 24/07 Booking

VIP Call Girls Palanpur 7001035870 Whatsapp Number, 24/07 Booking
Top Rated Pune Call Girls Budhwar Peth ⟟ 6297143586 ⟟ Call Me For Genuine Se...

Top Rated Pune Call Girls Budhwar Peth ⟟ 6297143586 ⟟ Call Me For Genuine Se...
Design For Accessibility: Getting it right from the start

Design For Accessibility: Getting it right from the start
Call Girls in Ramesh Nagar Delhi 💯 Call Us 🔝9953056974 🔝 Escort Service

Call Girls in Ramesh Nagar Delhi 💯 Call Us 🔝9953056974 🔝 Escort Service
Block diagram reduction techniques in control systems.ppt

Block diagram reduction techniques in control systems.ppt
Bhosari ( Call Girls ) Pune 6297143586 Hot Model With Sexy Bhabi Ready For ...

Bhosari ( Call Girls ) Pune 6297143586 Hot Model With Sexy Bhabi Ready For ...
(INDIRA) Call Girl Bhosari Call Now 8617697112 Bhosari Escorts 24x7

(INDIRA) Call Girl Bhosari Call Now 8617697112 Bhosari Escorts 24x7
8. analysis of truss part ii, method of section, by-ghumare s m
- 1. Analysis of Truss - Part-II (Method of Section ) Sub- Engg. Mechanics By: Mr. Ghumare S. M. Truss
- 2. Stability of Truss Depending on no. of members, stability of the truss is checked by using following equation. m = 2j-r r = No. of Reactions = 3 m = 2j-3 Where, m = Number of members, j = Number of Joints 1. m = 2j-3 -----Satisfied Eq. ----Stable Truss 1. m 2j-3 -----Not Satisfied Eq.----Unstable
- 3. Methods of Section Use: When forces in few members are required, method of section is used. Assumptions in the Analysis of Truss 1. Truss should be perfect truss 2. Self wt. of the truss members are neglected 3. External load acts on the joints only 4. All joints are assumed as hinge or pin joints 5. Members carrying axial loads only, Tension or Compression in nature. Sign Convention: Assume Tensile force +ve (T) and Compression force – ve (C)
- 4. Analysis of Truss using Method of Section Steps: 1. Draw F.B.D. of the given Truss, check stability if reqd. 2. Apply conditions of equilibrium to entire truss and find external reactions at supports 3. Take section or pass section through the members where forces to be determined. 4. At a time, section should not pass through more than three members. 5. Consider any one side of section i.e. L.H.S. or R.H.S. for analysis. 6. Apply conditions of Equilibrium to selected section. 7. Find the forces in the corresponding members.
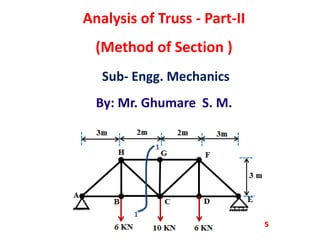
- 5. Example 1. Determine the forces in the members BC, HC and HG for the truss shown in Fig. State weather the forces are in tension or compression. To check stability of the truss: m = 2j-r , r = 3, m =13 , j =8 13 = 2x 8-3 , 13=16-3 , 13=13 Given truss is stable
- 6. Draw F.B.D. of the given Truss Solution: Draw F.B.D. Find angles E -1 H H θ = tan (3/2) θ = 56.30 Apply conditions of equim. and find reactions at supports 0 A = 0,xxF 0 Y E Y E A + R -6 - 10 - 6 = 0, A + R = 22 KN = 0, -(1) yF E A E E E -6 x 3 - 10 x 5 - 6 x 7 + R x10 =0, -18 - 50 - 42 + 10 x R =0 10 R = 110, R = 11 M =0 Anticlockwise KN( ), A = 11 N -V ( e K )y
- 7. L. H. S. R. H. S.
- 8. Consider L.H.S. Assume all are tensile Apply conditions of equim. 01. Y HC HC HC A - 6 - F sin56.3= 0, 11- 6 - F sin56.3 = 0, F = 6 KN (T) yF 2. , 3 @HG HC BC BC C H B F x 3 - 11 x = 0, F x 3 = Mome 33, F nt of F ,F 6 H = 11 = KN M = 0 0 (T) 03. HG BC HC HG HG HG F + F + F cos56.3 = 0, F + 11 + 6 x 0.554 = 0, F = -14.32 KN F = 14.32 KN (C) xF HC BC HGF = 6 KN (T), F = 11 KN (T) F = 14.32 KNAns: (C)
- 9. Example 2. Determine the forces in the members GF and GB for the truss shown in Fig. State nature of the forces. To check stability of the truss: m = 2j-r , r = 3, m =11 , j =7 11 = 2x 7-3 , 11=14-3 , 11=11 Given truss is stable
- 10. Draw F.B.D. of the given Truss and find support reactions Apply conditions of equillibrium. 0 A = 0,xxF 0 Y D Y D A + R -6 - 8 = 0, A + R = 14 KN = 0, (1) yF D A D D D -6 x 3.05 - 8 x 5.49 + R x 8.54 =0, -62.22 + 8.54 R = 0 8.54 R = 62.22, R = 7.285 KN( M =0 Anticlockwise ), A = 6.715 -V ( e KNy
- 11. Take section 1-1 Consider L.H.S.
- 12. Consider L.H.S. Assume all are tensile Apply conditions of equim. 01. Y GB GB GB A - F = 0, 6.715 - F = 0, F = 6.715 KN (T) yF 2. AB G AB AB GB GF F x 3.05 - Ay x 3.05 = 0, F x 3.05 - 6.715 x 3.05 = 0 Moment of F , , F = 6 F @ .71 G = 5 KN M =0 0 (T) 6.715 . 03 AB GF x GF GF HG F + F + A = 0, + F + 0 = 0, F = -6.715 KN F = 6.715 KN(C) xF GB AB HGF = 6.715 KN (T), F = 6.An 715 KN (T) F = 6.715 KNs: (C)
- 13. Example 3. Determine the forces in the members DF, DG and EG for the truss shown in Fig. State nature of the forces. To check stability of the truss: m = 2j-r , r = 3, m =21 , j =12 21 = 2x 12-3 , 21= 24-3 , 21=21 Given truss is stable
- 14. Draw F.B.D and Find support reactions y L y L y L Given loa A + R -2- d is Sy 2-2-2-2 =0 A + mmetric R = 10--------(1) A = 5KN( ), R = a 5 KN ) 0, ( l =yF 0 0 ,x x A F
- 15. To find forces in members pass section through DF, DG and EG Considering the L.H.S to find the forces in the members DF, DG and EG -1 D 0 D θ = tan (3/4) θ = 36.86
- 16. To find forces in members DF, DG and EG DG DG DG DG DG 5 - 2 - 2 - F sin36.86 =0, 1 - F sin36.86 =0, 1 - F sin36.86 =0 F = 1 F =0, / = 1.67KN(T sin36.86, ) yF EG EG EG EG EG D -A x 7 + 2 x 4 + F x 3 =0, -5 x 7 + 2 x 4 + F x 3 =0, -35 + 8 + F x 3=0, -27 + F x 3=0 F = 9K M =0 ) , N (T y
- 17. To find force in member DF X EG DF DG DF DF D F F F D D A + F + F + F cos36.86 = 0, 0 + 9 + F +1.67cos36.86 = 0, 9 + F + 1.67cos36.86 = 0, F + 1.67cos36.86 = -9, F = -10.33 F = 10.3 =0, 3 K KN N(C) XF
- 18. Thank You