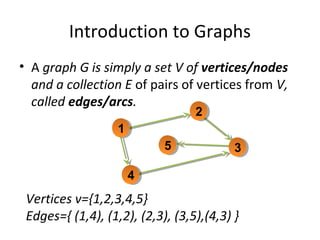
1. Introduction to Graphs
• A graph G is simply a set V of vertices/nodes
and a collection E of pairs of vertices from V,
called edges/arcs.
11
55
44
33
22
Vertices v={1,2,3,4,5}
Edges={ (1,4), (1,2), (2,3), (3,5),(4,3) }

2. • Some times edges have third component called
weight or cost. Such graphs are called weighted
graphs
• Edges in a graph are either directed or undirected.
• An edge {u,v} is said to be undirected if
edge (u,v) = edge (v,u)
• An edge (u,v) is said to be directed if (u,v) and
(v,u) edges are not same and represented by two
different lines.

3. • If all the edges in a graph are undirected, then
we say the graph is an undirected graph.
• a directed graph, also called a digraph, is a
graph whose edges are all directed.
• A graph that has both directed and undirected
edges is often called a mixed graph.

4. 11
55 44
33
22
11
55
44
33
22
verticesvertices
Undirected
Edge
Undirected
Edge
Directed
Edge
(1,4)
Directed
Edge
(1,4)

5. • Vetex u is adjacent to vertex v if there exists an
edge between u and v in the graph
• An edge is said to be incident on a vertex if the
vertex is one of the edge’s endpoints.

6. 11
55 44
33
22
11
55
44
33
22
vertices 1
and 2 are
adjacent
vertices 1
and 2 are
adjacent
Outgoing
Edges 2
Outgoing
Edges 2
Incoming
Edges 2
Incoming
Edges 2

7. • The degree of a vertex v, denoted deg(v), is
the number of incident edges of v. The in-
degree and out-degree of a vertex v are the
number of the incoming and outgoing edges
of v, and are denoted indeg(v) and outdeg(v),
respectively.
11
55
44
33
22
Degree of 3 is 3Degree of 3 is 3
In Degree of 3 is 2In Degree of 3 is 2
Out Degree of 3 is 1Out Degree of 3 is 1
Degree of 4 is 2Degree of 4 is 2
In Degree of 4 is 1In Degree of 4 is 1
Out Degree of 4 is 1Out Degree of 4 is 1

8. An edge (undirected or directed) is a self-loop
if its two endpoints coincide
An edge (undirected or directed) is a self-loop
if its two endpoints coincide
A graphs do not have parallel edges or self-
loops such graphs are said to be simple graph.
A graphs do not have parallel edges or self-
loops such graphs are said to be simple graph.

9. AA
CC
BB
DD
e1e1
e2e2
e3e3
e5e5
e4e4
AA
CC
BB
DD
self-loopself-loop
simplesimple

10. • Connected Graph: any two vertices are
connected by some path. All vertices can be
reached by all other vertices in graph
• Tree is a connected graph without cycles

11. • Simple path : no repeated vertex
Cycle: simple path, except that the last vertex is
same as the first

12. • Directed graphs that have no cycles are called
Directed acyclic graphs (DAG)
• A undirected graph is connected if there is a
edge from every vertex to every other vertex.
• Directed connected graphs are called strongly
connected

13. Real life situations that can be modelled by a graph
1) Airport System
Vetex : airports
Edges: flight routes
Edge cost: time, distance or cost
Graph is directed graph as cost may not be the same for
to and fro journey
Make sure the graph is strongly connected so that every
airport is connected
We must also determine the best path (having less cost)
between any 2 airports
Two vertices are connected by an edge is there exists a
non stop flight from the airports

14. Traffic Flow
• Vertex: each street intersection
• Edge : each street
• Edge cost: speed limit or capacity
• We can find shortest route or most likely
location for bottlenecks

15. 1. Adjacency Matrix1. Adjacency Matrix
2. Adjacency List2. Adjacency List
Graph RepresentationGraph Representation

16. Adjacency Matrix
• Assume V = {1, 2, …, n}
• An adjacency matrix represents the graph as a
n x n matrix A:
– A[i, j] = 1 if edge (i, j) ∈ E (or weight of edge)
= 0 if edge (i, j) ∉ E
– Storage requirements: O(V2
)
• A dense representation

17. AA
CC
BB
DD
1. Adjacency Matrix1. Adjacency Matrix
AA BB CC DD
AA
BB
CC
DD
00 11 00 11
11 00 11 11
00 11 00 11
11 11 11 11

18. AA
CC
BB
DD
1. Adjacency Matrix1. Adjacency Matrix
AA BB CC DD
AA
BB
CC
DD
00 11 00 11
00 00 11 11
00 00 00 00
00 00 11 11
For a digraph (= directed graph), the row sum is the
out_degree, while the column sum is the in_degree

19. AA
DD
BB
CC
2. Adjacency List2. Adjacency List
AAAA
BBBB
CCCC
DDDD
BBBB DDDD
DDDD
AAAA BBBB DDDD
AAAA

20. Adjacency ListAdjacency List
An undirected graph with n vertices and e edges
has n head nodes and 2e list nodes in
adjacency list
Nodes that have direct edges are only added as
list nodes to that node.
In the above example, node A has direct edges
with node B and node D

21. Graph Traversals
Graph traversal is a technique used for searching vertex in a
graph. The graph traversal is also used to decide the order of
vertices to be visited in the search process. A graph traversal
finds the edges to be used in the search process without
creating loops. That means using graph traversal we visit all the
vertices of graph without visiting the vertices that are already
visited.
Two types of graph traversals
1.Breadth first search (BFS)
2.Depth first search (DFS)
BFS and DFS produces a spanning tree as final result.
BFS are implemented using Queues and DFS using Stacks

22. Step 1: Start
Step 2: Read the graph
Step 3:Define a Queue of size = total number of vertices in the graph.
Step 4: Mark all the vertices as unvisited.
Step 5:Select any node as starting vertex (say v1). Insert v1 into queue.
Step 6: Visit all the non-visited adjacent vertices of the vertex which is at front of
the Queue and insert them into the Queue and mark them visited.
Step 7- When there is no new vertex to be visited from the vertex which is at front
of the Queue then delete that vertex.
Step 8 - Repeat steps 6 and 7 until queue becomes empty.
Step 9- When queue becomes empty, then produce final spanning tree by
removing unused edges from the graph
Step 10: stop
Breadth-First Search Algorithm

23. #include<stdio.h>
int a[20][20],q[20],visited[20],n,f=-1,r=-1;
void bfs(int v)
{
int i;
for (i=0;i<n;i++) // check all the vertices in the graph
{
if(a[v][i] != 0 && visited[i] == 0) // adjacent to v and not visited
{
r=r+1;
q[r]=i; // insert them into queue
visited[i]=1; // mark the vertex visited
printf("%d ",i);
}
}
f=f+1; // remove the vertex at front of the queue
if(f<=r) // as long as there are elements in the queue
bfs(q[f]); // peform bfs again on the vertex at front of the queue
}
Entire program is at below link
http://enthusiaststudent.blogspot.com/2019/03/breadth-first-search-c-program.html
BFS Program

25. BFS traversal is A ->
BFS traversal is A -> D -> E -> B

26. BFS traversal is A -> D -> E -> B
BFS traversal is A -> D -> E -> B -> C -> F

27. BFS traversal is A -> D -> E -> B -> C -> F
BFS traversal is A -> D -> E -> B -> C -> F -> G

28. BFS traversal is A -> D -> E -> B -> C -> F -> G
BFS traversal is A -> D -> E -> B -> C -> F -> G

29. BFS traversal is A -> D -> E -> B -> C -> F -> G

30. Depth-First Search Algorithm
Step 1 - Define a Stack of size = total number of vertices in the graph.
Step 2 - Select any vertex as starting point for traversal. Visit that vertex and
push it on to the Stack.
Step 3 - Visit any one of the non-visited adjacent vertices of a vertex which is
at the top of stack and push it on to the stack.
Step 4 - Repeat step 3 until there is no new vertex to be visited from the vertex
which is at the top of the stack.
Step 5 - When there is no new vertex to visit then use back tracking and pop
one vertex from the stack.
Step 6 - Repeat steps 3, 4 and 5 until stack becomes Empty.
Step 7 - When stack becomes Empty, then produce final spanning tree by
removing unused edges from the graph

31. #include<stdio.h>
int a[20][20],q[20],visited[20],n;
void dfs(int v)
{
int i;
for (i=0;i<n;i++) // check all the vertices in the graph
{
if(a[v][i] != 0 && visited[i] == 0) // adjacent to v and not visited
{
visited[i]=1; // mark the vertex visited
printf("%d ",i);
dfs(i);
}
}
}
Entire program is at below link
http://enthusiaststudent.blogspot.com/2019/03/depth-first-search-c-program.html
DFS Program

33. DFS traversal is A

34. DFS traversal is A -> B

35. DFS traversal is A -> B -> C

36. DFS traversal is A -> B -> C -> E

37. DFS traversal is A -> B -> C -> E -> D

38. DFS traversal is A -> B -> C -> E -> D

39. DFS traversal is A -> B -> C -> E -> D -> F

40. DFS traversal is A -> B -> C -> E -> D -> F -> G

41. DFS traversal is A -> B -> C -> E -> D -> F -> G

42. DFS traversal is A -> B -> C -> E -> D -> F -> G

43. DFS traversal is A -> B -> C -> E -> D -> F -> G

44. DFS traversal is A -> B -> C -> E -> D -> F -> G

45. DFS traversal is A -> B -> C -> E -> D -> F -> G

46. DFS traversal is A -> B -> C -> E -> D -> F -> G

47. DFS traversal is A -> B -> C -> E -> D -> F -> G

48. Topological sorting for Directed Acyclic Graph (DAG) is a
linear ordering of vertices such that for every directed edge (u,v),
vertex u comes before v in the ordering. Topological Sorting for a
graph is not possible if the graph is not a DAG.
For example : consider a graph represents the course
prerequisite structure at a university.
A directed edge (v,w) indicates that course v must be completed
before course w may be attempted. A topological ordering of these
courses is any course sequence that does not violate the prerequisite
requirement.
It is clear that a topological ordering is not possible if the graph
has a cycle, since for two vertices v and w on the cycle, v precedes w
and w precedes v. Furthermore, the ordering is not necessarily
unique; any legal ordering will do.
Topological Sort

49. Step 1: Identify vertices that have no incoming edges
•
•
If no such vertices, graph has only cycle(s) (cyclic graph)
Topological sort not possible – Halt.
B
C
A
Example of a cyclic graph
D
Topological Sort

50. Step 1: Identify vertices that have no incoming edges
• The “in-degree” of these vertices is zero
B
C
A
F
D E
Topological Sort

51. Step 2: Delete this vertex of in-degree 0 and all
its outgoing edges
output.
B
A
from the graph. Place it in the
C
AF
D E
Topological Sort

52. Repeat Step 1 and Step 2 until graph is empty
Select
B
C
AF
D E
Topological Sort

53. B
Select B. Copy to sorted list. Delete B and its edges.
B
C
A BF
D E

54. C
Select C. Copy to sorted list. Delete C and its edges.
C
A B CF
D E

55. D
Select D. Copy to sorted list. Delete D and its edges.
DA B CF
D E

56. E, F
Select
Select
E.
F.
Copy
Copy
to
to
sorted
sorted
list.
list.
Delete
Delete
E and its edges.
F and its edges.
DA B C E FF
E

57. Done
B
C
A
F
Remove from algorithm
and serve.D E
DA B C E F

58. Topological Ordering Algorithm:
Example
58
v1
Topological order:
v2 v3
v6 v5 v4
v7 v1

59. Topological Ordering Algorithm:
Example
59
v2
Topological order: v1
v2 v3
v6 v5 v4
v7

60. Topological Ordering Algorithm:
Example
60
v3
Topological order: v1, v2
v3
v6 v5 v4
v7

61. Topological Ordering Algorithm:
Example
61
v4
Topological order: v1, v2, v3
v6 v5 v4
v7

62. Topological Ordering Algorithm:
Example
62
v5
Topological order: v1, v2, v3, v4
v6 v5
v7

63. Topological Ordering Algorithm:
Example
63
v6
Topological order: v1, v2, v3, v4, v5
v6
v7

64. Topological Ordering Algorithm:
Example
64
v7
Topological order: v1, v2, v3, v4, v5, v6
v7

65. Minimum spanning trees
A spanning tree for a connected graph G (V,E) with n vertices is a tree
containing all the vertices of G and n-1 edges. The spanning tree must be
connected and must not have cycles.
The cost of the spanning tree is the sum of the weights of all the edges in the tree.
There can be many spanning trees. Minimum spanning tree is the spanning tree
where the cost is minimum among all the spanning trees. There also can be many
minimum spanning trees.

66. Minimum Spanning Tree Algorithms
Kruskal’s algorithm
1. Select the shortest edge in the
graph
2. Select the next shortest edge
which does not create a cycle
3. Repeat step 2 until all vertices
have been connected
Prim’s algorithm
1. Select any vertex
2. Select the shortest edge
connected to that vertex which
does not create a cycle
3. Select the shortest edge
connected to any vertex already
connected which does not
create a cycle
4. Repeat step 3 until all vertices
have been connected

67. A cable company want to connect five villages to their network which
currently extends to the market town of Tirupati. What is the minimum
length of cable needed?
Tirupathi kadapa
Vijayawada
Bangalore
kurnool
Chennai
2
7
4
5
8 6
4
5
3
8
Example

68. We model the situation as a network, then the
problem is to find the minimum spanning tree for the
network
A F
B C
D
E
2
7
4
5
8 6
4
5
3
8

69. A
F
B
C
D
E
2
7
4
5
8 6
4
5
3
8
List the edges in
order of size:
ED 2
AB 3
AE 4
CD 4
BC 5
EF 5
CF 6
AF 7
BF 8
CF 8
Kruskal’s Algorithm

70. Select the shortest
edge in the network
ED 2
Kruskal’s Algorithm
A
F
B
C
D
E
2
7
4
5
8 6
4
5
3
8

71. Select the next shortest
edge which does not
create a cycle
ED 2
AB 3
Kruskal’s Algorithm
A
F
B
C
D
E
2
7
4
5
8 6
4
5
3
8

72. Select the next shortest
edge which does not
create a cycle
ED 2
AB 3
CD 4 (or AE 4)
Kruskal’s Algorithm
A
F
B
C
D
E
2
7
4
5
8 6
4
5
3
8

73. Select the next shortest
edge which does not
create a cycle
ED 2
AB 3
CD 4
AE 4
Kruskal’s Algorithm
A
F
B
C
D
E
2
7
4
5
8 6
4
5
3
8

74. Select the next shortest
edge which does not
create a cycle
ED 2
AB 3
CD 4
AE 4
BC 5 – forms a cycle
EF 5
Kruskal’s Algorithm
A
F
B
C
D
E
2
7
4
5
8 6
4
5
3
8

75. All vertices have been
connected.
The solution is
ED 2
AB 3
CD 4
AE 4
EF 5
Total weight of tree: 18
Kruskal’s Algorithm
A
F
B
C
D
E
2
7
4
5
8 6
4
5
3
8

76. A
F
B
C
D
E
2
7
4
5
8 6
4
5
3
8
Select any vertex
A
Select the shortest
edge connected to
that vertex
AB 3
Prim’s Algorithm

77. A
F
B
C
D
E
2
7
4
5
8 6
4
5
3
8
Select the shortest
edge connected to
any vertex already
connected.
AE 4
Prim’s Algorithm

78. Select the shortest
edge connected to
any vertex already
connected.
ED 2
Prim’s Algorithm
A
F
B
C
D
E
2
7
4
5
8 6
4
5
3
8

79. Select the shortest
edge connected to
any vertex already
connected.
DC 4
Prim’s Algorithm
A
F
B
C
D
E
2
7
4
5
8 6
4
5
3
8

80. Select the shortest
edge connected to
any vertex already
connected.
EF 5
Prim’s Algorithm
A
F
B
C
D
E
2
7
4
5
8 6
4
5
3
8

81. Prim’s Algorithm
A
F
B
C
D
E
2
7
4
5
8 6
4
5
3
8
All vertices have been
connected.
The solution is
AB 3
AE 4
ED 2
DC 4
EF 5
Total weight of tree: 18

82. •Both algorithms will always give solutions with the
same length.
•They will usually select edges in a different order
– you must show this in your workings.
•Occasionally they will use different edges – this
may happen when you have to choose between
edges with the same length. In this case there is
more than one minimum connector for the
network.
Some points to note