El documento trata sobre las matrices. Define una matriz como un arreglo de elementos dispuestos en filas y columnas. Explica que una matriz se denota con una letra mayúscula entre paréntesis y se indican sus dimensiones como subíndices. Describe las propiedades de las matrices como la suma, resta, multiplicación por un escalar, producto y transpuesta.

1. Resolución de
Problemas Matemáticos I
Docente: Demetrio
CCESA RAYME
Algebra de Matrices

2. DEFINICIÓN
Dimensión de la matriz n
m
2ª columna
3ª fila














a11 a12 a13 ...... a1n
a21 a22 a23 ...... a2n
a31 a32 a33 ...... a3n
.. .. .. .. ..
am1 am2 am3 ...... amn
= (aij)
A= (aij)
i = 1,2…,m
j = 1,2…,n
Se llama matriz de orden m×n a todo conjunto rectangular de
elementos aij dispuestos en m líneas horizontales (filas) y n
verticales (columnas) de la forma:
MATRICES

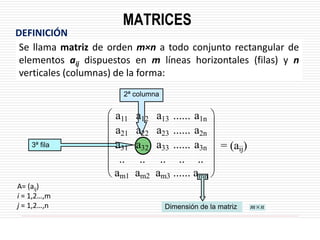
3. Definición:
Es un arreglo de elementos dispuestos
en “m” filas y “n” columnas.
El nombre de la matriz se escribe con
letra mayúscula entre paréntesis
rectangulares (corchetes).
La cantidad de las filas y de columnas
de una matriz, se indican como
subíndice después del nombre de la
matriz. El primer índice corresponde a
las filas y el segundo a las columnas.
Ejemplo:
[A] mxn
Los elementos de una matriz
también se presentan entre
paréntesis rectangulares
(corchetes).
5 −8 9
0 −7 0
0 −4 −6
[A] 3X3=
MATRICES

4. Orden de una Matriz
Es la cantidad de filas y columnas de la matriz.
Se lee: matriz de orden m por n
Matriz de 4 por 3
5 −8 9
0 −7 0
1
0
8
−4
7
−6
[B] 4x3=
MATRICES

5. Matriz Cuadrada
Es aquella matriz cuyo número
de filas es igual al número de
columnas.
Ejemplo [B] 3X3
1 -4 5
-2 4 0
4 5 2
Se lee matriz de tercer orden
MATRICES

6. Matriz Rectangular
Es aquella matriz cuyo número
de filas es diferente al número
de columnas.
Ejemplo [B]3,4
1 -4 5 3
-2 4 0 -2
4 5 2 6
MATRICES

7. Diagonal Principal
Es la línea en que quedan ubicados los elementos
a11, a22,a33,a44 ... (número de columna = número de la fila)
de la matriz.
La Diagonal principal.
Ejemplo:
Elementos de la diagonal principal:
5, -7 y 7










−
−
7
8
10
0
7
0
9
8
5
MATRICES

8. Traza de una matriz cuadrada, es la suma algebraica de
los valores de los elementos de la diagonal principal.
Ejemplo:
La Traza de la matriz es Traza = 5 –7 +7 = 5










−
−
7
5
13
0
7
0
9
8
5
MATRICES
( )
n
ii 11 22 nn
i 1
Traz A a a a ................ a
=
= = + + +


9. Suma de dos matrices
Sean dos matrices conformables
para la suma (mismo orden), se
define la suma como:
[C] m,n = [A] m,n + [B] m,n
La matriz [C] tendrá el mismo
orden de [A] ó [B].
Cada elemento de C es la suma del
correspondiente elemento de [A] y
[B]
ci,j = ai,j + bi,j
Para i = 1,2 .....m y j = 1,2 ......n
+ =





 −
9
7
2
3






−
−
5
7
4
8





−
14
0
2
5
MATRICES

10. MATRICES

11. Resta de dos matrices
Sean dos matrices
conformables para la resta
(mismo orden), se define la
resta como:
[C] m,n= [A] m,n - [B] m,n
La matriz [C] tendrá el mismo
orden de [A] ó [B].
Cada elemento de C es la resta algebraica
de los correspondientes elementos de [A] y
[B]
ci,j = ai,j - bi,j
Para i = 1,2 .....m y j = 1,2 ......n
Ejemplo
- =





 −
9
7
2
3






−
−
5
7
4
8





 −
4
14
6
11
MATRICES

12. MATRICES

13. MATRICES
1 2 3 3 2 5
A ; B
0 2 1 1 3 4
   
− −
= =
   
   
−
   








−
−
=
+
5
5
1
2
4
2
B
A 







−
−
−
=
−
3
1
1
8
0
4
B
A

14. Propiedades del Calculo Matricial
Sean tres matrices conformables para la suma y k un escalar
[A]m,n , [B]m,n , [C]m,n
[A] + [B] = [B] + [A] Ley Conmutativa
[A] +( [B] + [C] ) = ( [A] + [B] )+ [C] Ley Asociativa
k ( [A] + [B] ) = k [A] + k [B] = ( [A] + [B] )k Ley Distributiva
MATRICES

15. Producto de una matriz por un escalar
Sea k un escalar y la matriz [A]m,n, se define la muliplicación de una
matriz por un escalar como
[ C ]m,n = k [A]m,n
En donde ci,j = k ai,j (i=1,2,3....m; j=1,2,3...n)
Ejemplo
[C] = 3 [A] = 3 =





 −
9
7
2
3





 −
27
21
6
9
MATRICES

16. MATRICES
2 1 0
A
3 4 5
 
−
=  
 
−
 








−
−
=
15
12
9
0
3
6
3A

17. MATRICES

18. 2 3 5 7
AxB
4 5 2 1
−
  
=   
−
  
(fila 1)(columna 1)
2x5 3x2
− +
4x5 ( 5)x2
+ −
(fila 2)(columna 1)
(fila 1)(columna 2)
2x7 3x1
− +
4x7 ( 5)x1
+ −
(fila 2)(columna 2)
 
=  
 
2 3 5 7
AxB
4 5 2 1
−
   
=    
−
   
Multiplicación de Matrices. Para efectuar el producto de dos
matrices, se requiere que el número de columnas de la primera
matriz sea igual que el número de renglones de la segunda.
Cuando esto sucede, se dice que las matrices son conformables para
la multiplicación. Esto es, si A es de orden p x n y B es de orden n x q
el orden de la matriz producto es p x q
4 11
10 23
− −
 
=  
 

19. MATRICES

20. x =
Multiplicación de Matrices
[C]mxn= [A]mxp x [B]qxn
Son conformables para la Multiplicación si y solo si p = q
1 0 2
2 3 1






0
1
1
2






2
5
0
3
1
4
MATRICES

21. MATRICES
TRANSPUESTA DE UNA MATRIZ
Se llama transpuesta de A, y se representa por AT, a aquella matriz construida
a partir de la matriz A intercambiando sus filas por sus respectivas columnas.
La primera fila de A es la primera columna de AT, la segunda fila de A es la
segunda columna de AT, etc. De la definición se deduce que si A es de orden
m x n, entonces AT es de orden n x m.
T
ij ji
mxn nxm
Si : A a A a
   
=  =
   
2 1
A 3 5
7 4
 
−
 
=  
 
 
T
2 3 7
A
1 5 4
 
=  
 
−
 

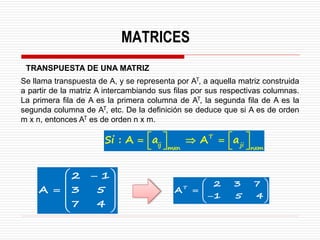
22. Matriz Transpuesta
Se denotar como [A]
[A] = [A] =
T
2
−3
1
7
−4
5
2
1
−4
−3
7
5
MATRICES
T

23. Matriz Identidad [ I ] o Unidad
Es una matriz cuadrada cuyo valor de los elementos de la diagonal
principal es uno y valor cero en todos los demás elementos.
[ I ] =










1
0
0
0
1
0
0
0
1
MATRICES
÷
÷
÷
ø
ö
ç
ç
ç
è
æ
=
1
0
0
0
1
0
0
0
1
I3
I

24. Matriz Cero o Nula
Es una matriz cuadrada en la cual el valor de todos los
elementos es cero.
Ejemplo










0
0
0
0
0
0
0
0
0
[ 0 ] =
[ 0 ] =
MATRICES

25. Matriz Opuesta o Negativa.
- [A]
Se obtiene de la matriz [A]
multiplicando cada elemento
por el escalar -1










−
−
1
2
8
9
5
4
4
2
1
Ejemplo
Sea la matriz
[A] =
-1 [A] =










−
−
−
−
−
−
−
1
2
8
9
5
4
4
2
1
MATRICES

26. Matrices Iguales
Son aquellas que tienen el mismo orden y cada
elemento de una es igual al correspondiente elemento
de la otra.
[A] = [B] ai,j = bi,j para i =1,2,3.... m j =1, 2,3... n
Ejemplo










−
−
0
7
5
8
7
6
2
4
3










−
−
0
7
5
8
7
6
2
4
3
=
MATRICES

27. Matrices Conmutativas
Son aquellas matrices para las cuales se cumple :
Sean [A] y [B] matrices cuadradas tales que
[A] x [B] = [B] x [A]
=






1
4
4
1






1
4
4
1






3
6
6
3






3
6
6
3
MATRICES
x x

28. Matriz Diagonal
Es una matriz cuadrada en la cual el valor de todos los
elementos son cero excepto en la diagonal.
[ A ] =
2 0 0
0 −3 0
0 0 1
MATRICES
÷
÷
÷
ø
ö
ç
ç
ç
è
æ
-
=
1
0
0
0
3
0
0
0
2
D
A

29. Matriz Escalar
Es una matriz cuadrada en la cual el valor de todos los
elementos son cero excepto en la diagonal principal, que tienen
el mismo valor.
a11 =a22 =a33 =a44 = k donde k es un escalar
2 0 0
0 2 0
0 0 2
A = A = 2 [ I ]
MATRICES
÷
÷
÷
ø
ö
ç
ç
ç
è
æ
=
2
0
0
0
2
0
0
0
2
A

30. MATRICES
Matriz
nula
Matriz
diagonal
Matriz
escalar
Matriz
unidad
Tiene todos sus
elementos iguales a
cero.
Todos los elementos
que no están en la
diagonal principal son
0.
Matriz diagonal en la
que todos los
elementos de la
diagonal principal son
iguales.
Matriz escalar en la
que todos los
elementos de la
diagonal principal son
1.
Ejemplo: Ejemplo: Ejemplo: Ejemplo:
0 0 0
N
0 0 0
 
=  
 
 
1 0 0
D 0 6 0
0 0 3
 
 
=  
 
 
3 0 0
E 0 3 0
0 0 3
 
 
=  
 
 
3
1 0 0
I 0 1 0
0 0 1
 
 
=  
 
 

31. Matriz Triangular Superior
Es una matriz cuadrada cuyos
elementos en la parte superior de la
diagonal principal y en ella, el valor es
diferente de cero.
El valor de los elementos abajo
de la diagonal principal es cero
ai j = 0 para i > j
Ejemplo:
1 3 6
0 −2 3
0 0 4
MATRICES
÷
÷
÷
ø
ö
ç
ç
ç
è
æ
-
=
4
0
0
3
2
0
6
3
1
T
A

32. Ejemplo Matriz Triangular Inferior
Es una matriz cuadrada cuyos
elementos en la parte inferior de la
diagonal principal y en ella, el valor es
diferente de cero.
El valor de los elementos arriba de la
diagonal principal es cero.
ai j = 0 para i < j
1 0 0
3 −2 0
3 5 4
MATRICES
÷
÷
÷
ø
ö
ç
ç
ç
è
æ
-
=
4
5
3
0
2
3
0
0
1
T
A

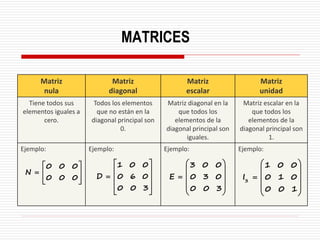
33. Matrices simétricas
Aquellas que cumplen con:
[A] = [A]
Propiedad
Si [A] es una matriz
cuadrada
[A] + [A] es simétrica
Ejemplo:
la matriz [A] es simétrica ya que:










−
2
5
8
5
1
4
8
4
3










−
2
5
8
5
1
4
8
4
3
[A] =
[A] =
MATRICES
T
T
T

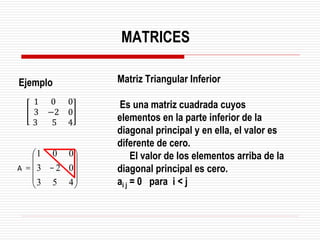
34. Matriz Antisimétrica o
Hemisimétrica
Es una matriz cuadrada que es
igual a la opuesta (o negativa) de
su transpuesta.
Necesariamente los elementos de
la diagonal principal tienen el valor
de cero.
[A] = - 1 [A]
Ejemplo:
La matriz [A] es antisimétrica ya que:
0 4 8
−4 0 5
−8 −5 0
0 4 8
−4 0 5
−8 −5 0
-1 [A] =
[A] =
MATRICES
T
T

35. Matriz Idempotente
Ejemplo










−
−
−
−
−
3
2
1
4
3
1
4
2
2
[A] x [A] = [A]
[A] =
MATRICES