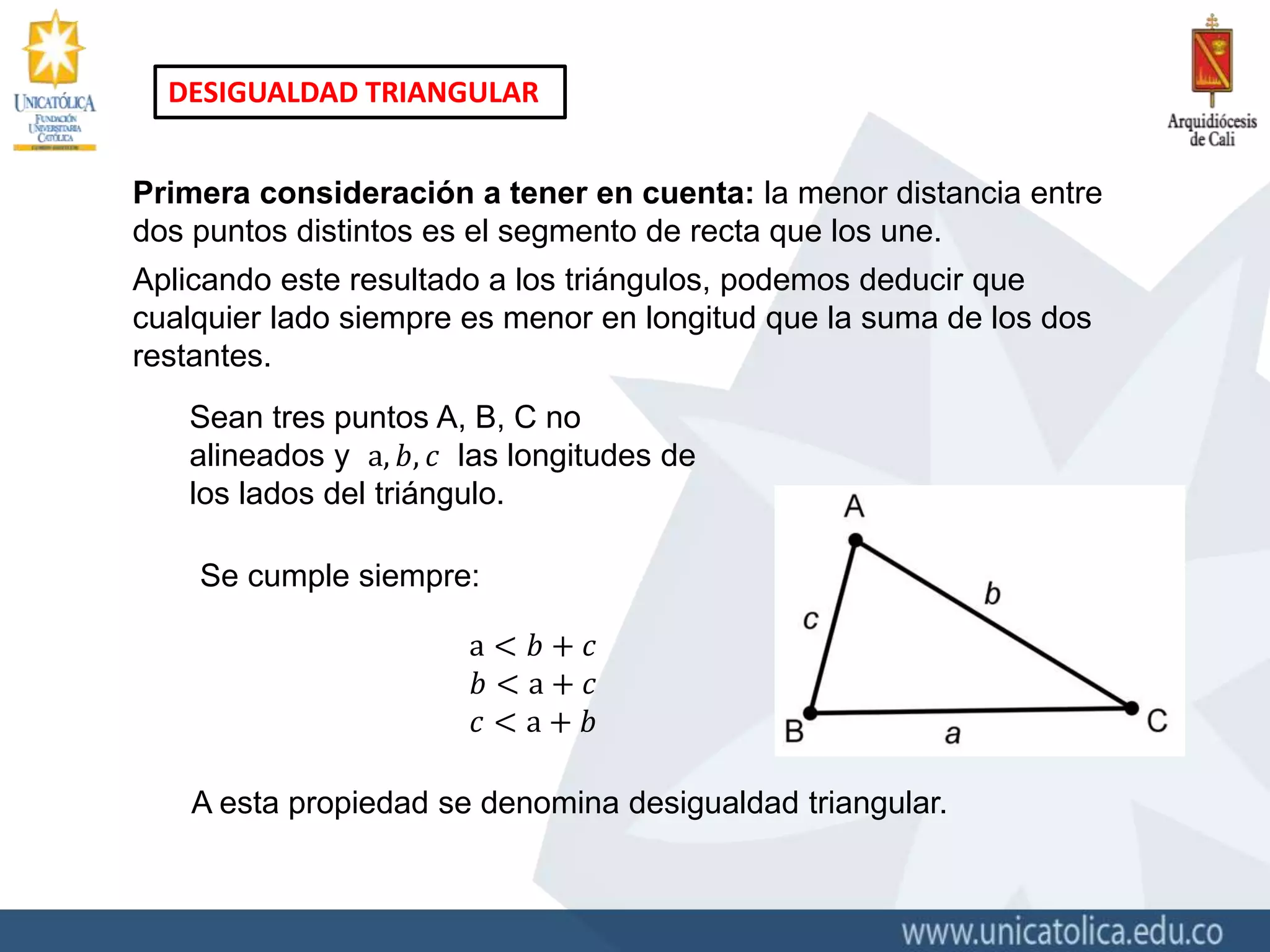
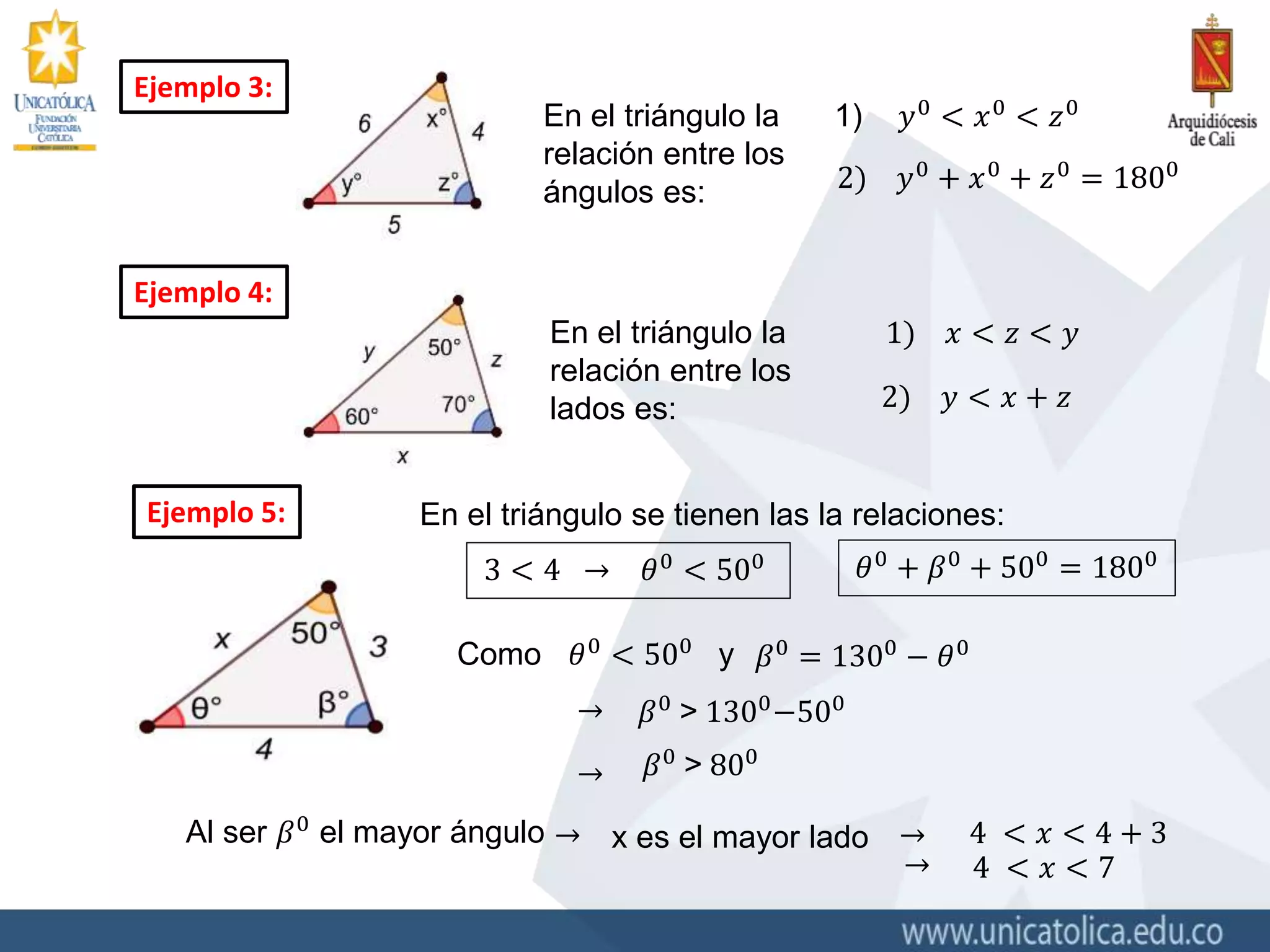
La desigualdad triangular establece que la longitud de cualquier lado de un triángulo siempre es menor que la suma de las longitudes de los otros dos lados. El documento explica este principio y proporciona ejemplos para determinar si tres segmentos corresponden a los lados de un triángulo aplicando la desigualdad triangular.

1. DESIGUALDAD TRIANGULAR
Primera consideración a tener en cuenta: la menor distancia entre
dos puntos distintos es el segmento de recta que los une.
Aplicando este resultado a los triángulos, podemos deducir que
cualquier lado siempre es menor en longitud que la suma de los dos
restantes.
a < 𝑏 + 𝑐
𝑏 < a + 𝑐
𝑐 < a + 𝑏
Sean tres puntos A, B, C no
alineados y a, 𝑏, 𝑐 las longitudes de
los lados del triángulo.
Se cumple siempre:
A esta propiedad se denomina desigualdad triangular.

2. Ejemplo 1:
Determinar las posibles longitudes del lado de
un triángulo si se sabe que las longitudes de los
otros dos de lados son 5 m y 3 m
Si se trata del lado mayor, entonces, su
longitud debe ser menor que la suma de
las longitudes de los otros dos lados.
𝑥 < 5 + 4 → 𝑥 < 9
Si 𝑥 no se trata del lado mayor, entonces
el lado mayor mide 5 m y su longitud debe
ser menor que la suma de los otros dos
lados
5 < 𝑥 + 4 → 5 − 4 < 𝑥
→ 1 < 𝑥
De las dos desigualdades anteriores se deduce
1 < 𝑥 < 9

3. A continuación aparecen diferentes longitudes de tres
segmentos. Establecer en cada caso si corresponden a
las longitudes de un triángulo
Ejemplo 2:
𝟏) 5𝑚, 10𝑚, 3𝑚
Solución: El lado mayor de los tres lados es 10𝑚
Al aplicar la desigualdad triangular se obtiene
10 < 5 + 3 → 10 < 8
Por no cumplir la desigualdad triangular, las longitudes
no corresponden a los lados de un triangulo
2) 3𝑚, 2𝑚, 3𝑚
Solución: Aquí se toma cualquiera de los dos segmentos de
longitud 3𝑚 como el lado mayor de los lados.
3 < 2 + 3 → 3 < 5
Al aplicar la desigualdad triangular se obtiene
Como se cumple la desigualdad triangular, las longitudes
si corresponden a los lados de un triángulo

4. Relaciones entre lados y ángulos de un triangulo
En un triángulo:
• Si dos ángulos no son congruentes, entonces los lados opuestos a
ellos tampoco son congruentes y el lado menor se opone al ángulo
menor.
𝛽0
< 𝜃0
→ 𝑏 < 𝑎
• Si dos lados no son congruentes,
entonces los ángulos opuestos a ellos
tampoco son congruentes y el ángulo
menor es el opuesto al lado menor
𝑏 < 𝑎 → 𝛽0
< 𝜃0

5. Ejemplo 3:
En el triángulo la
relación entre los
ángulos es:
1) 𝑦0
< 𝑥0
< 𝑧0
Ejemplo 4:
En el triángulo la
relación entre los
lados es:
1) 𝑥 < 𝑧 < 𝑦
2) 𝑦0
+ 𝑥0
+ 𝑧0
= 1800
2) 𝑦 < 𝑥 + 𝑧
Ejemplo 5: En el triángulo se tienen las la relaciones:
Como
3 < 4 → 𝜃0 < 500 𝜃0
+ 𝛽0
+ 500
= 1800
𝜃0
< 500
y
→
𝛽0
= 1300
− 𝜃0
𝛽0
> 1300
−500
→ 𝛽0
> 800
Al ser 𝛽0 el mayor ángulo → x es el mayor lado → 4 < 𝑥 < 4 + 3
4 < 𝑥 < 7→