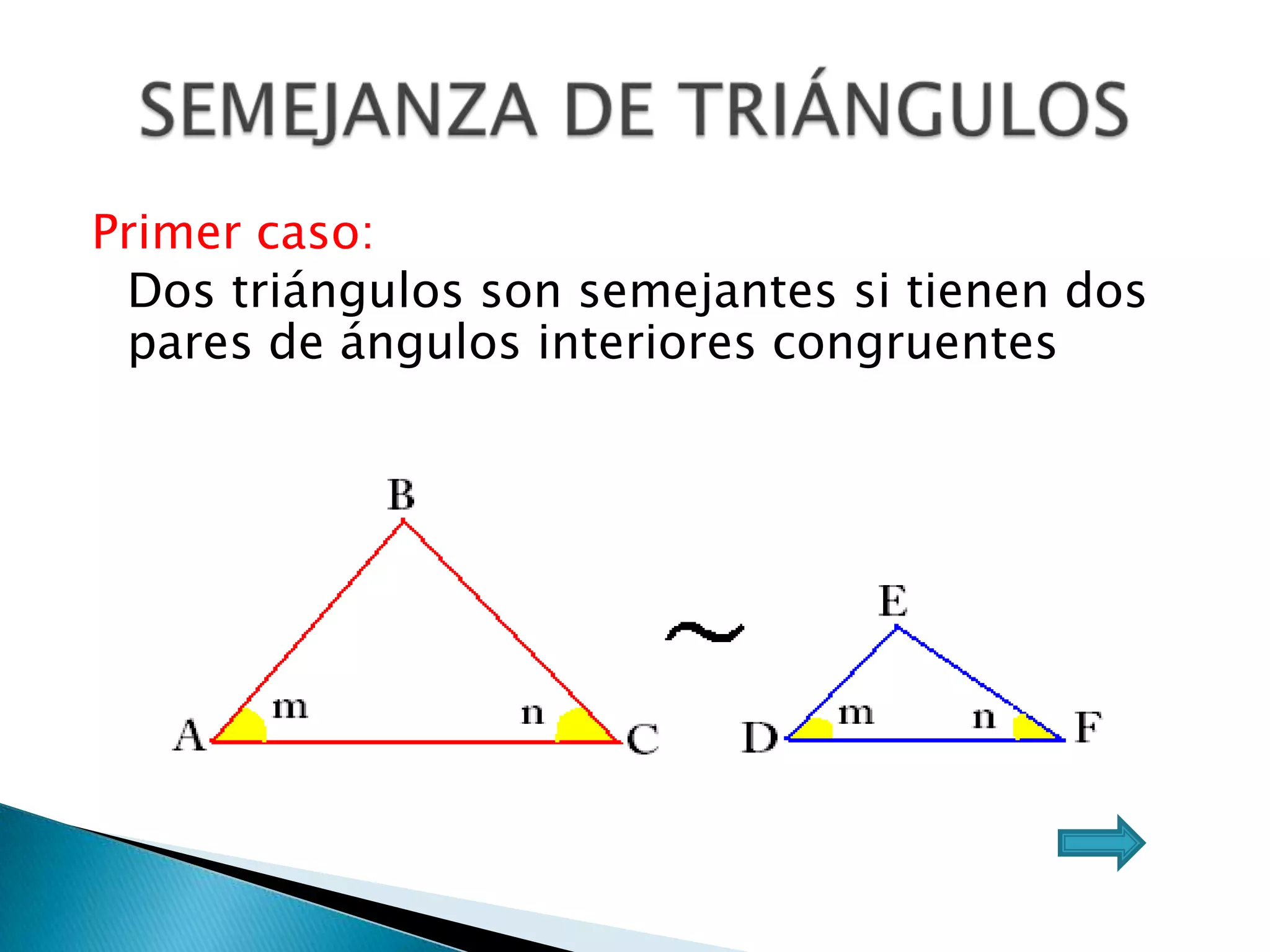
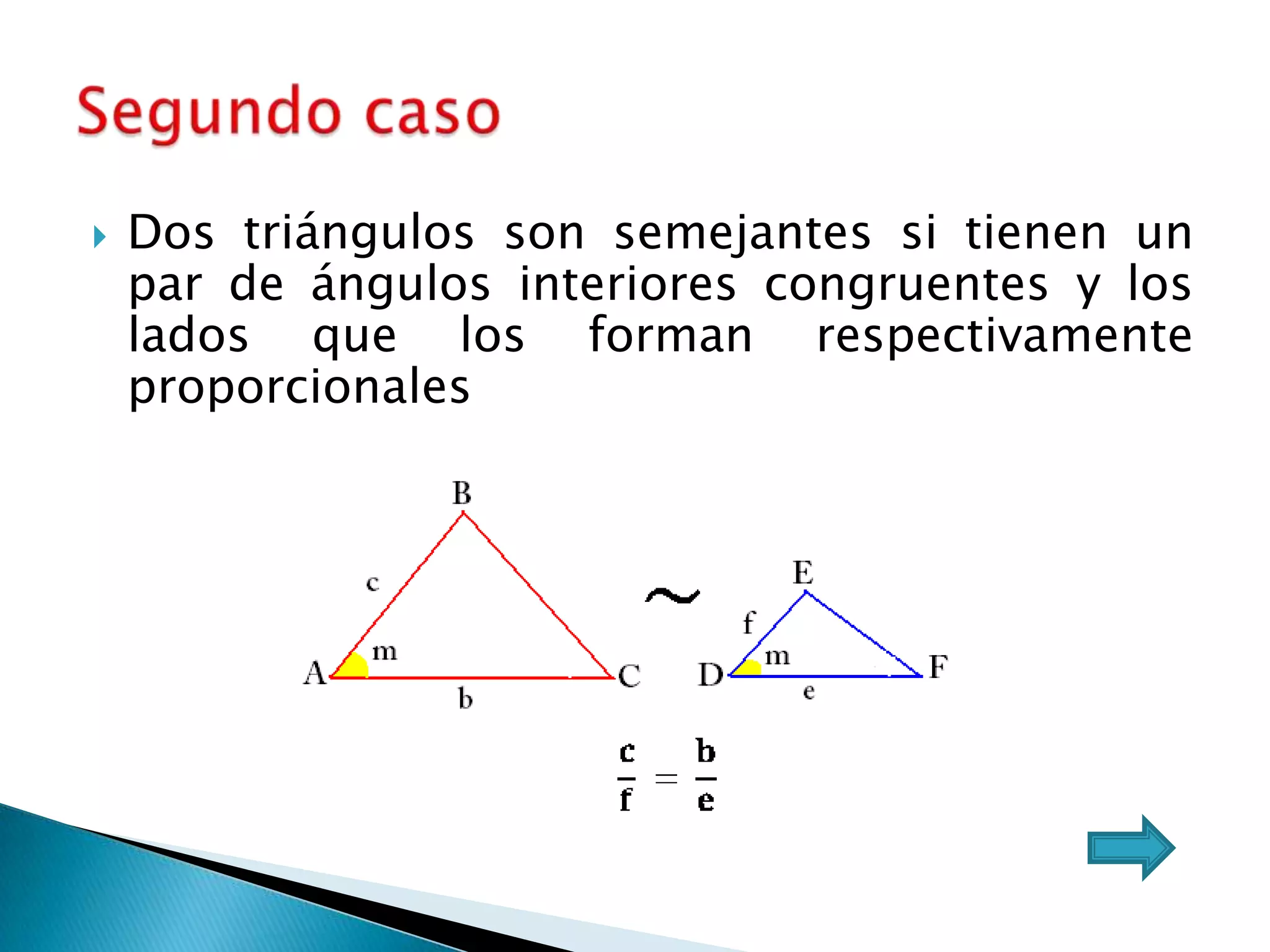
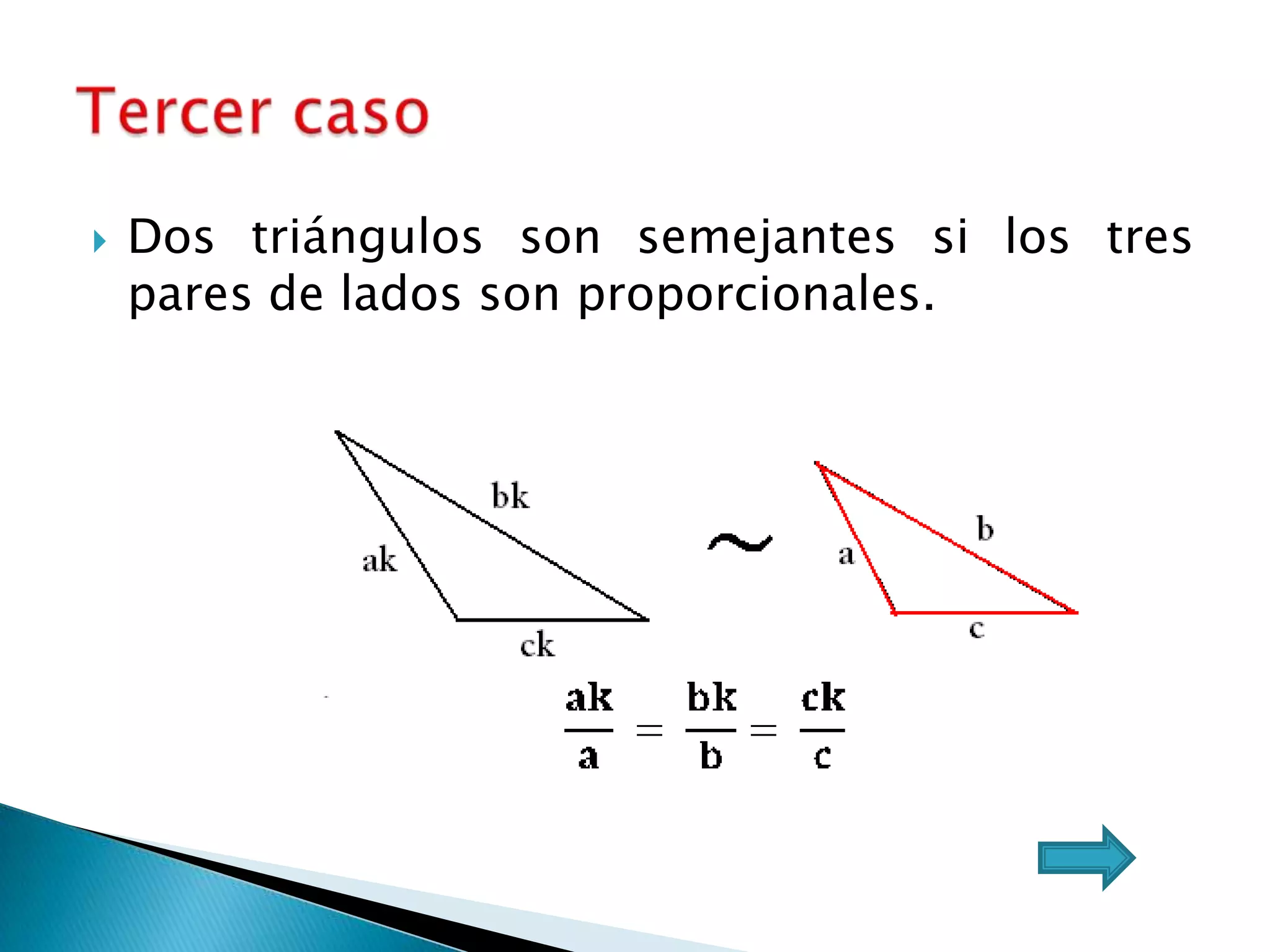
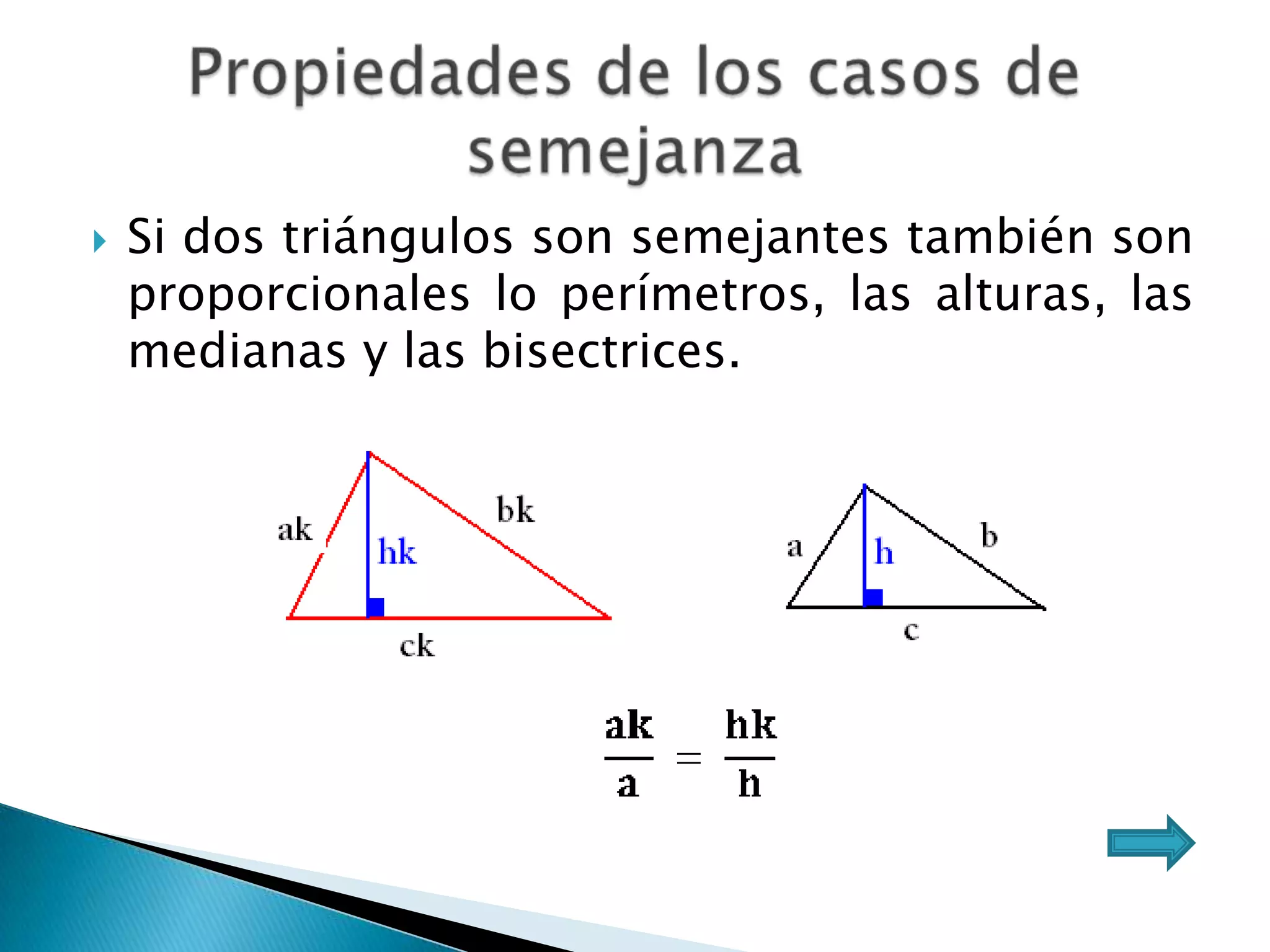
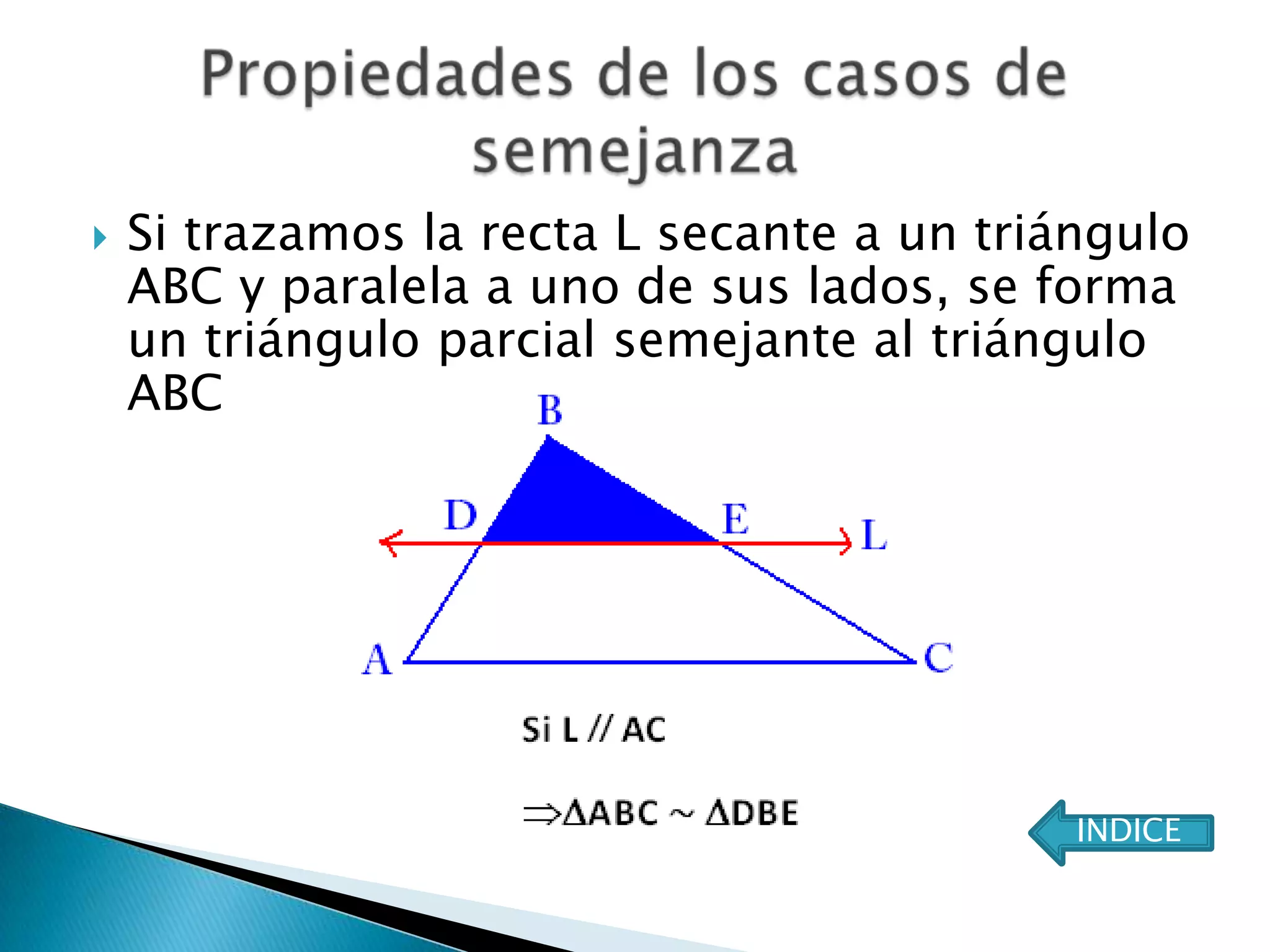
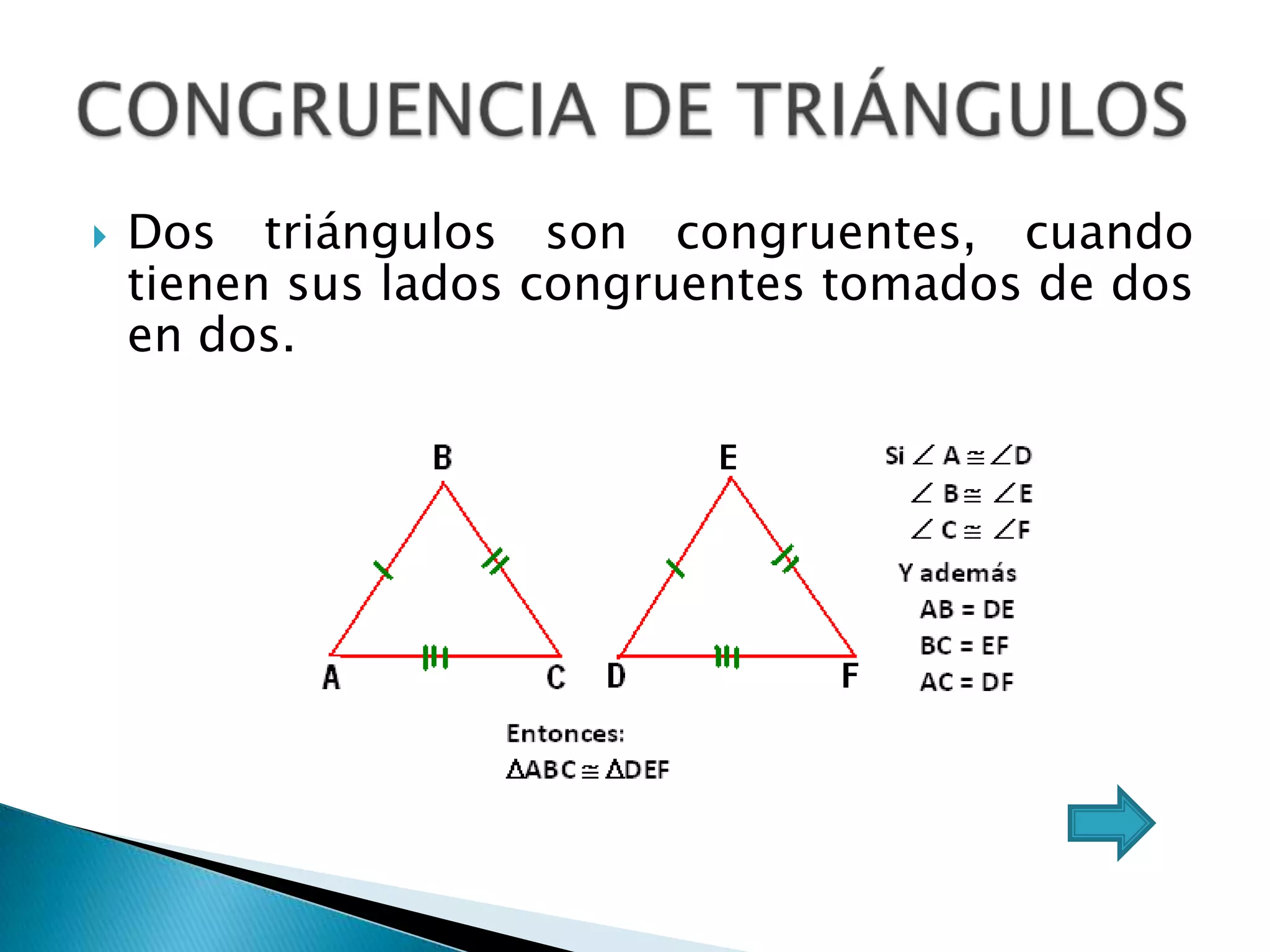
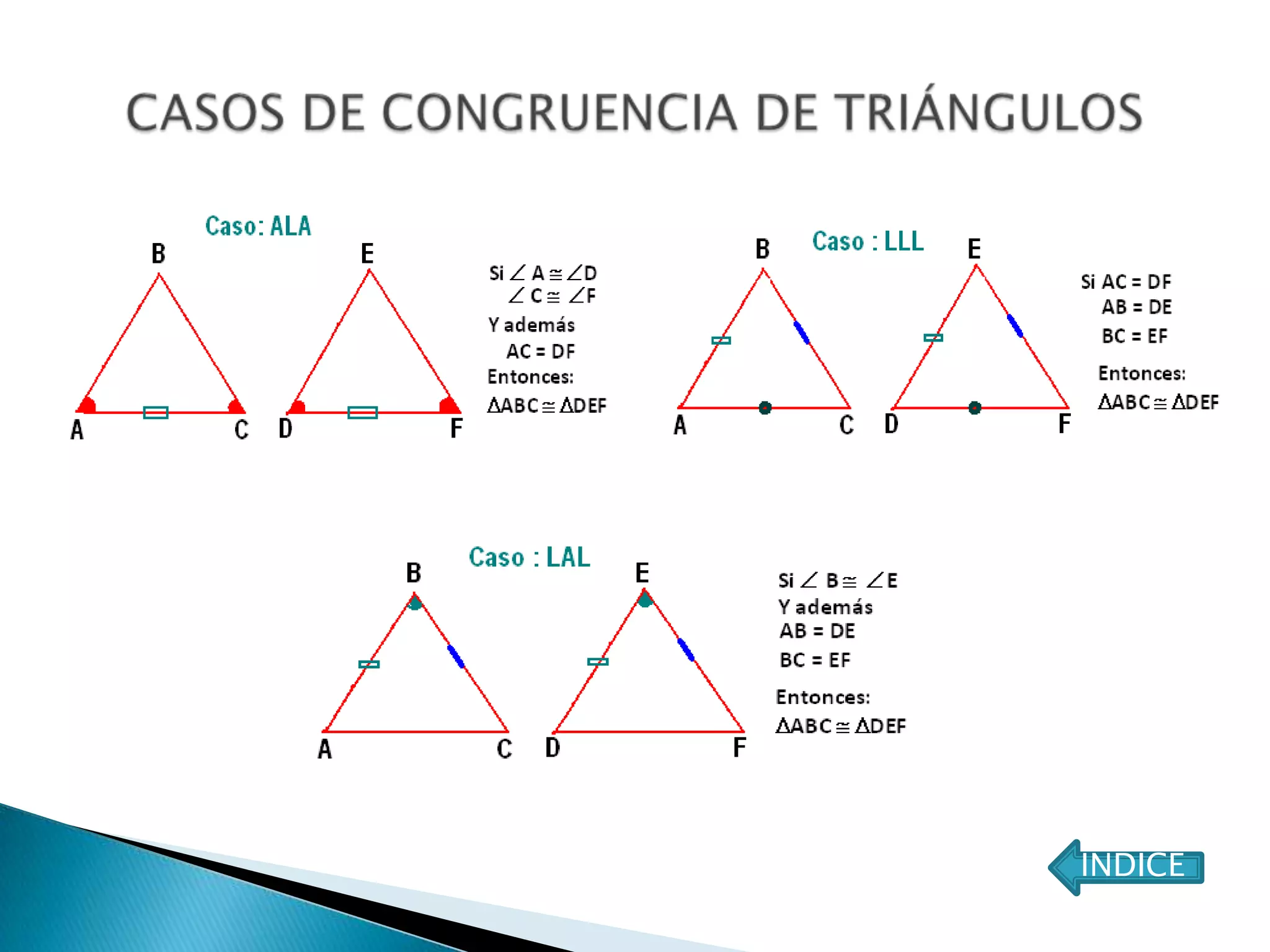
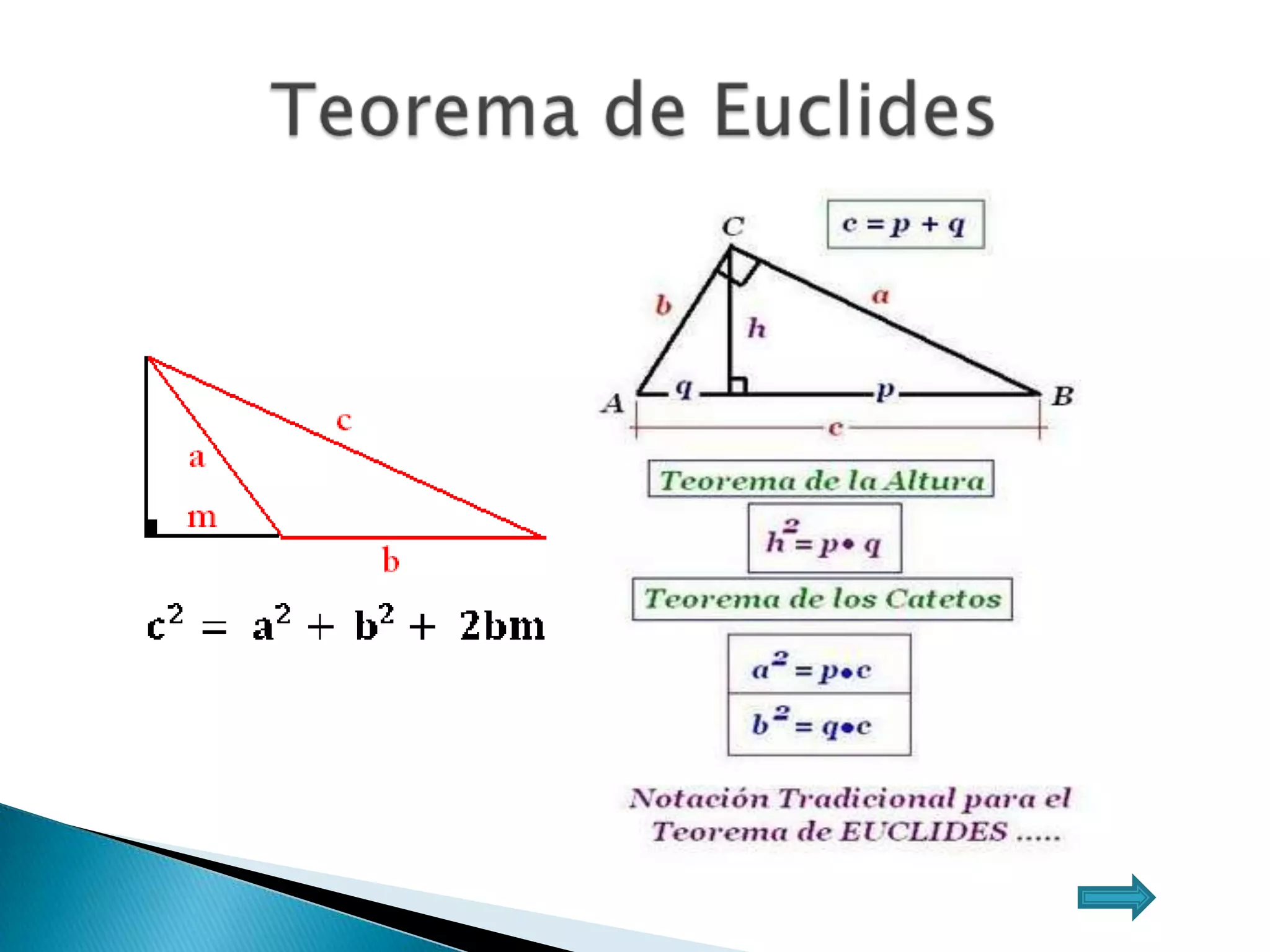
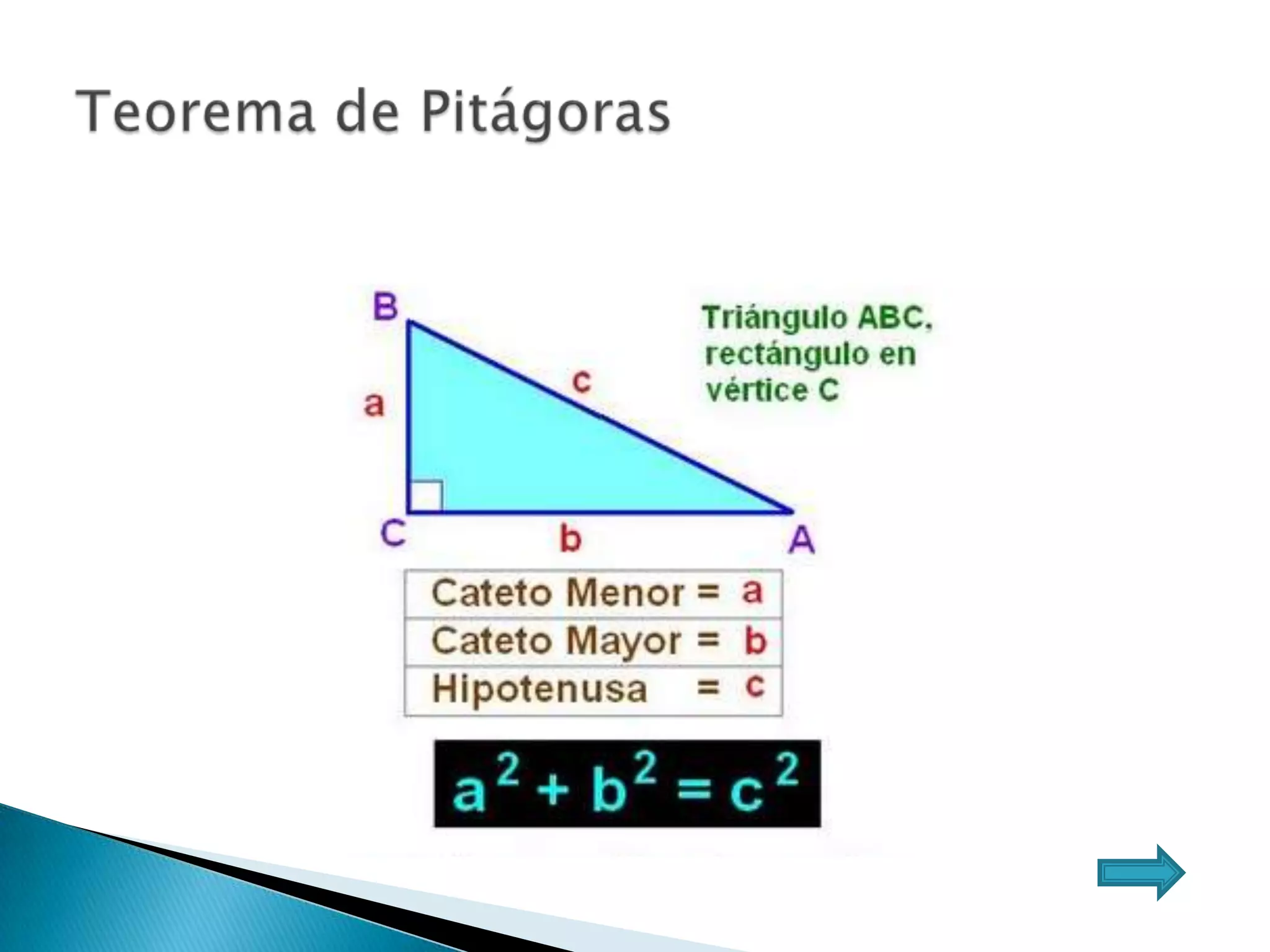
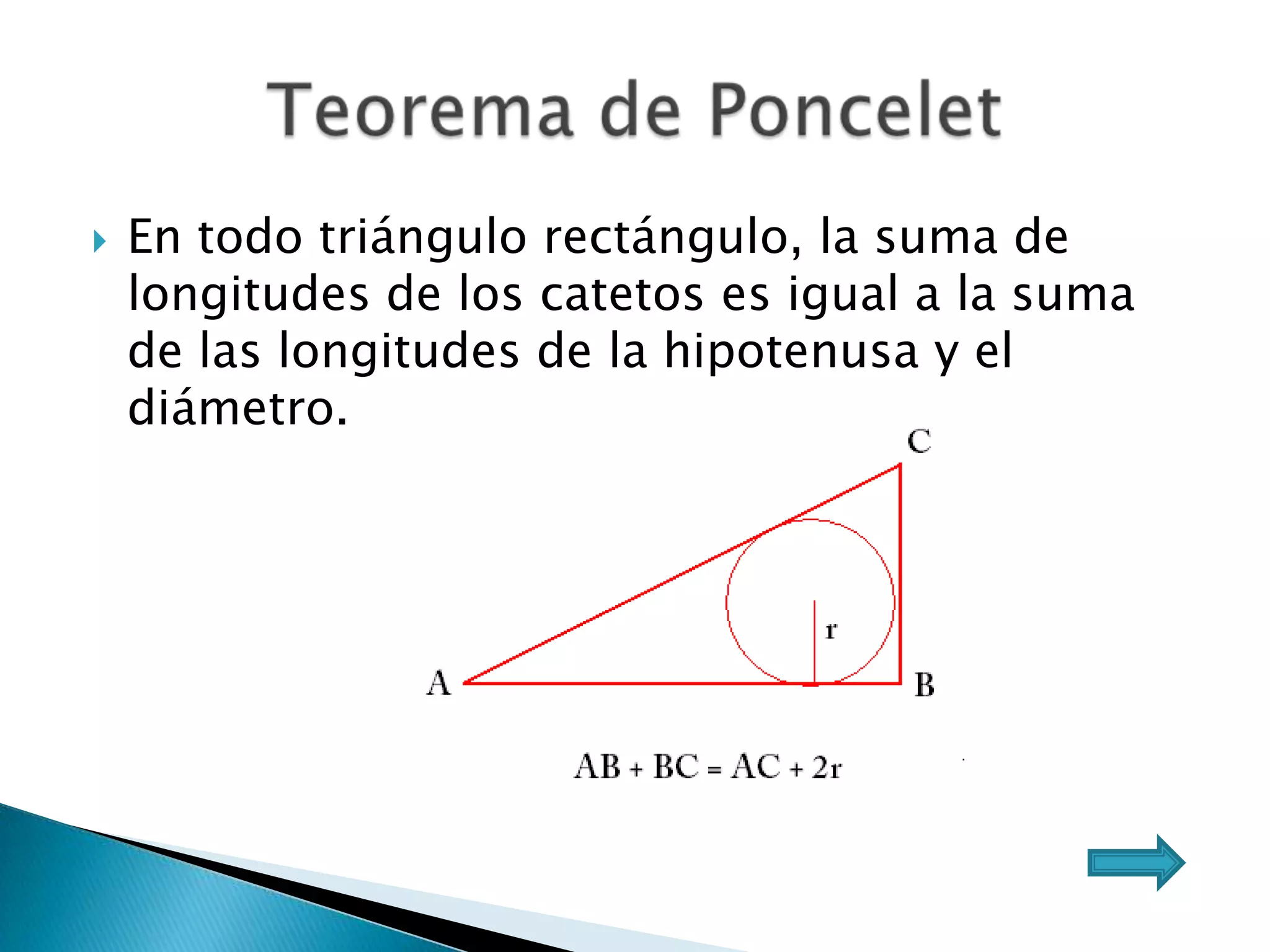
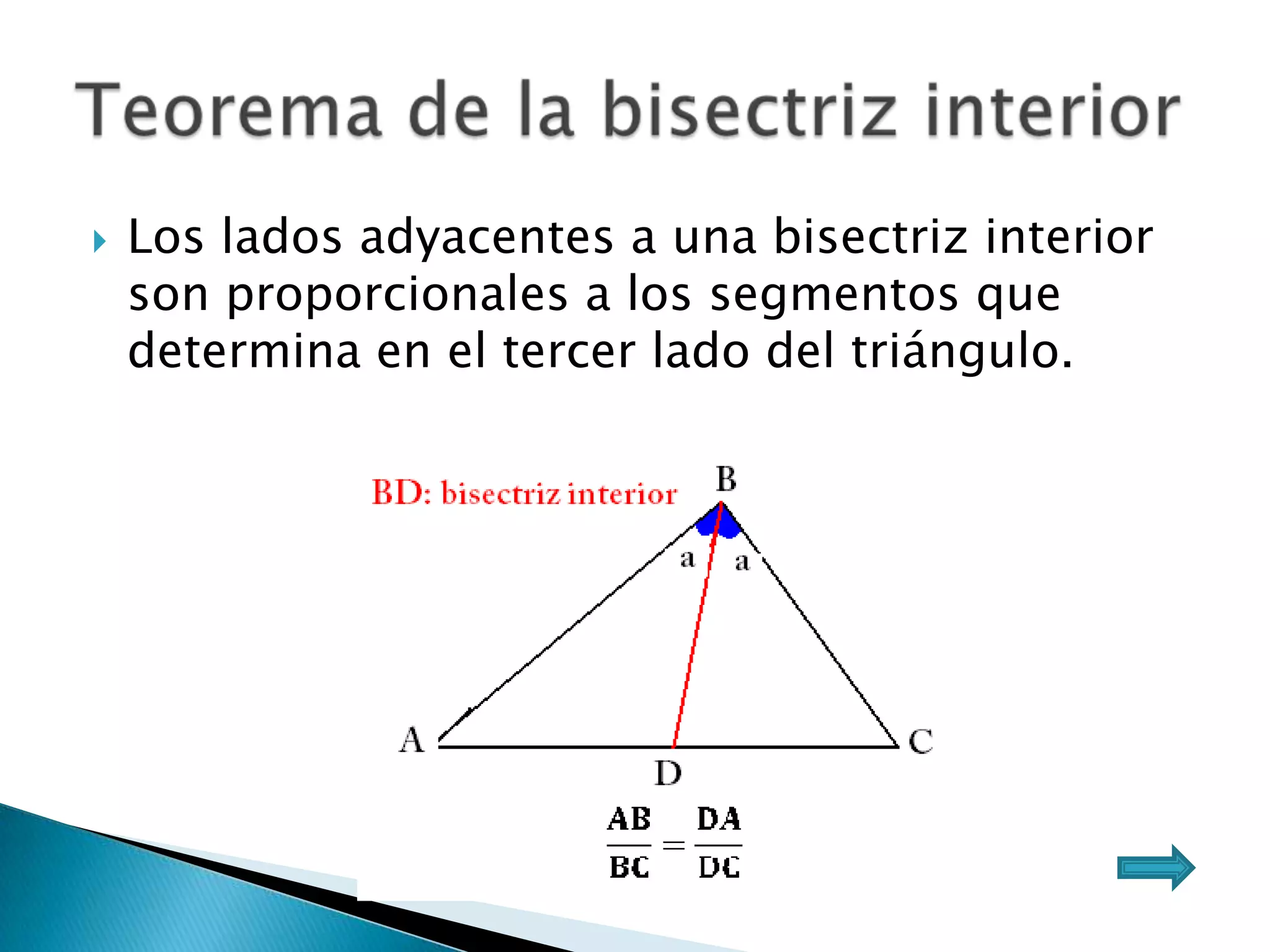
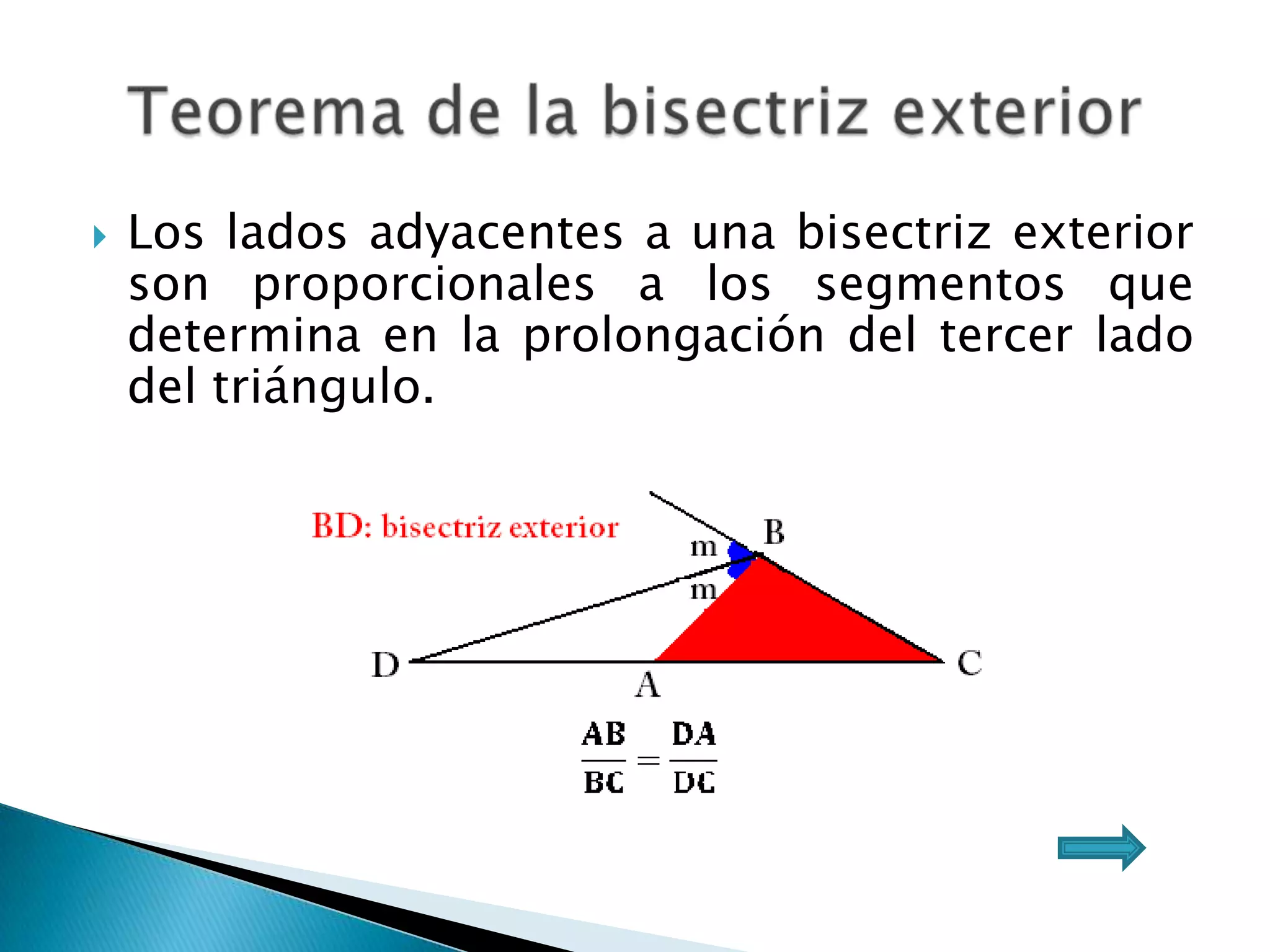
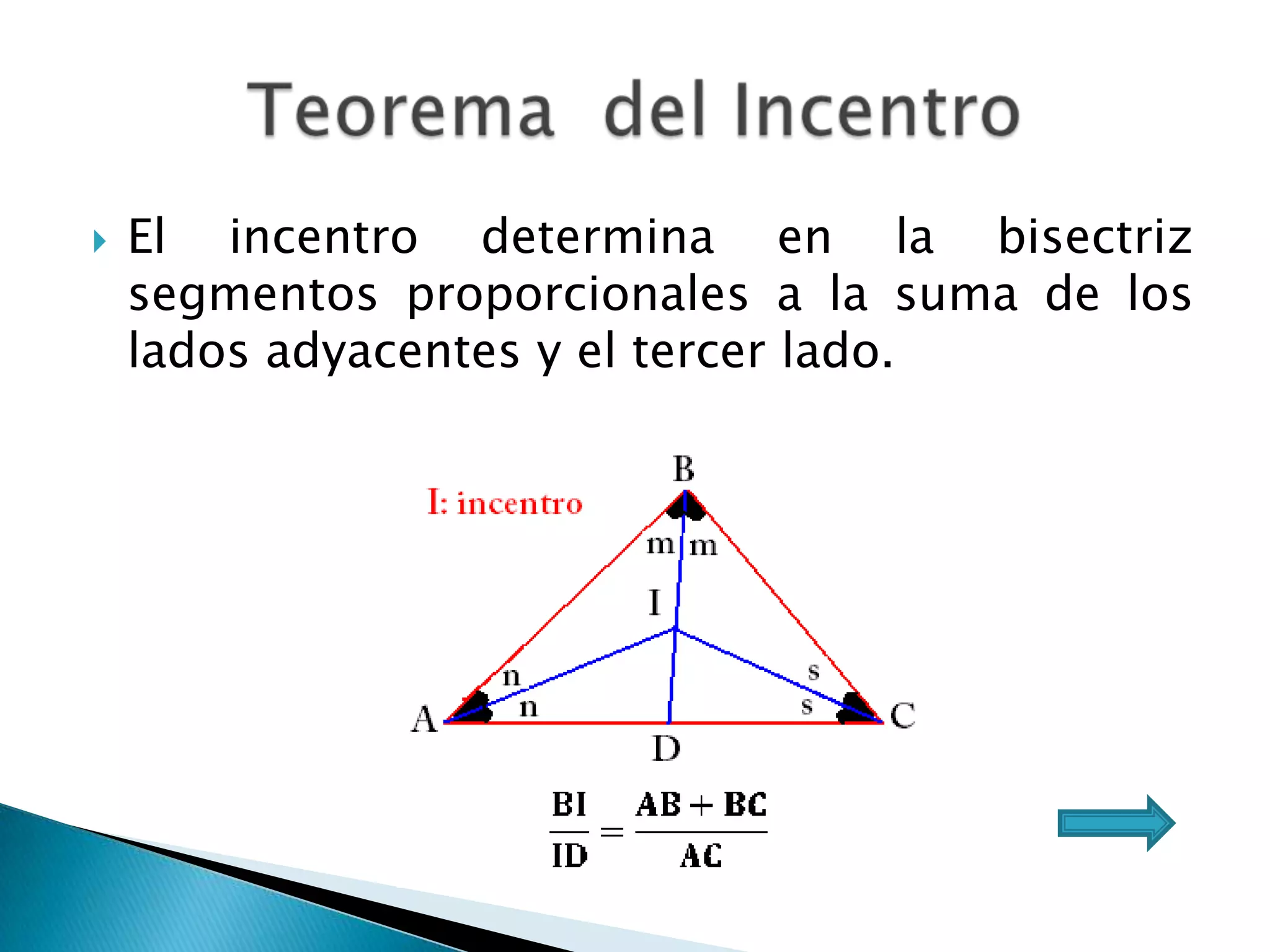
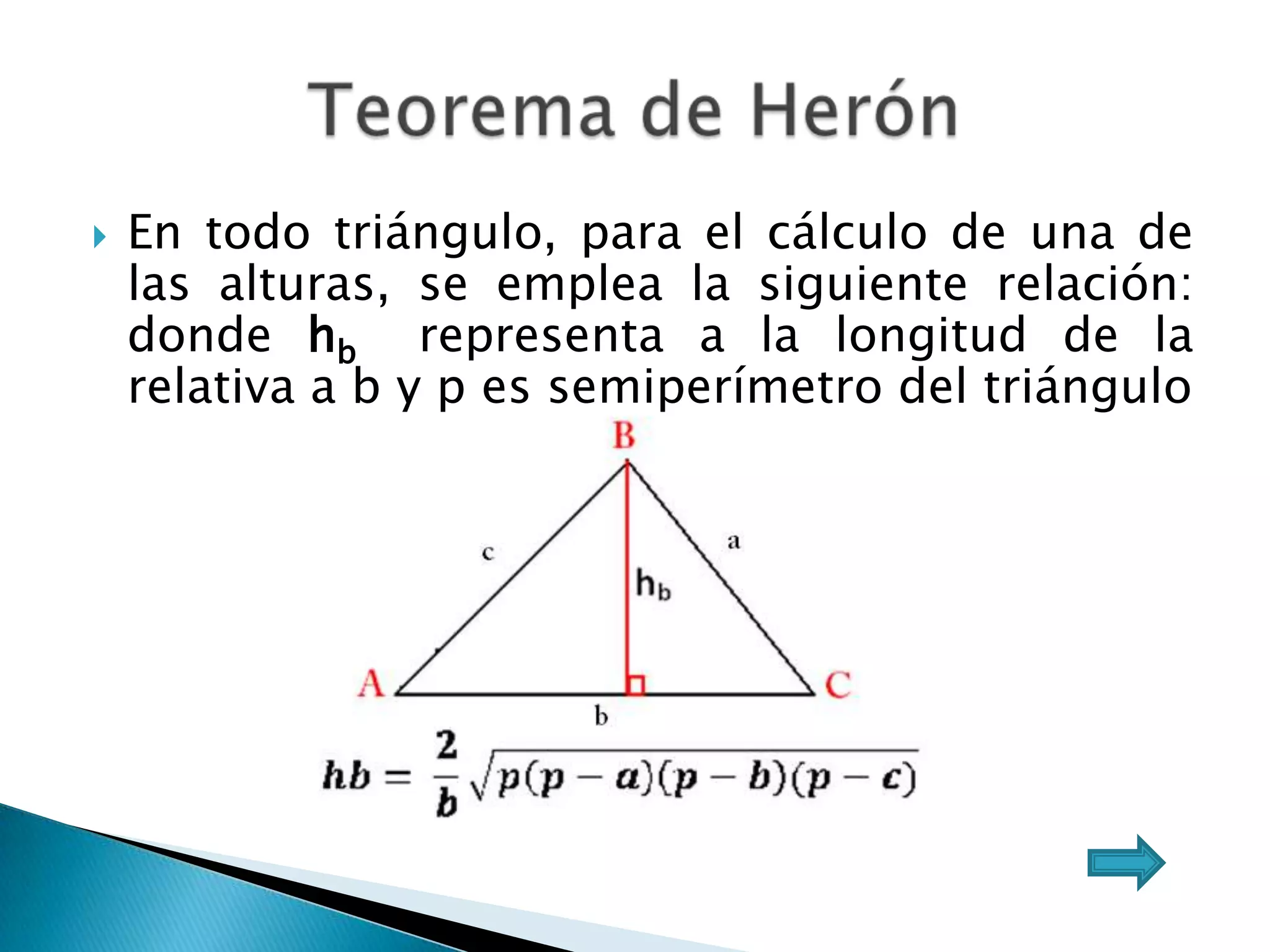
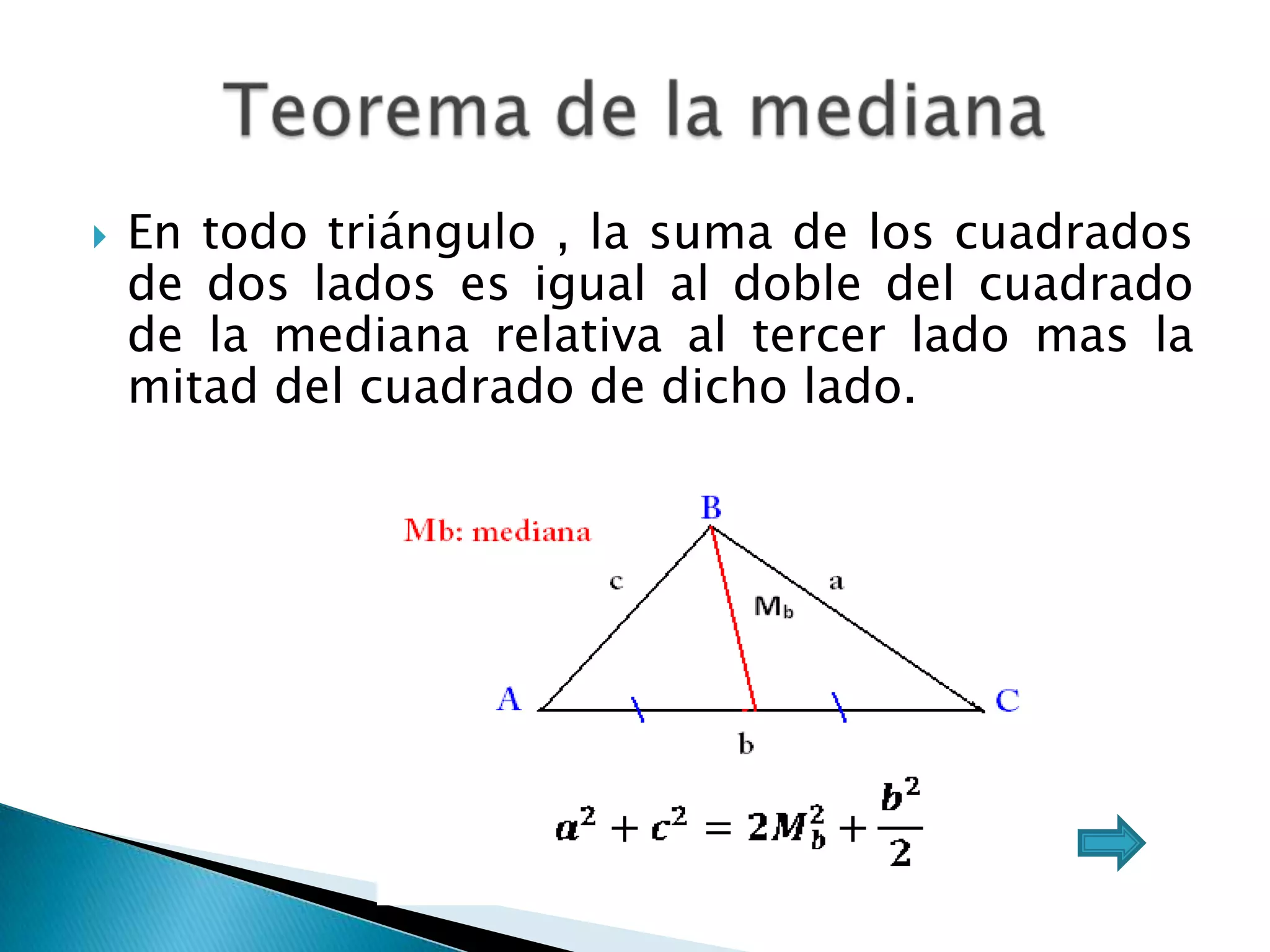
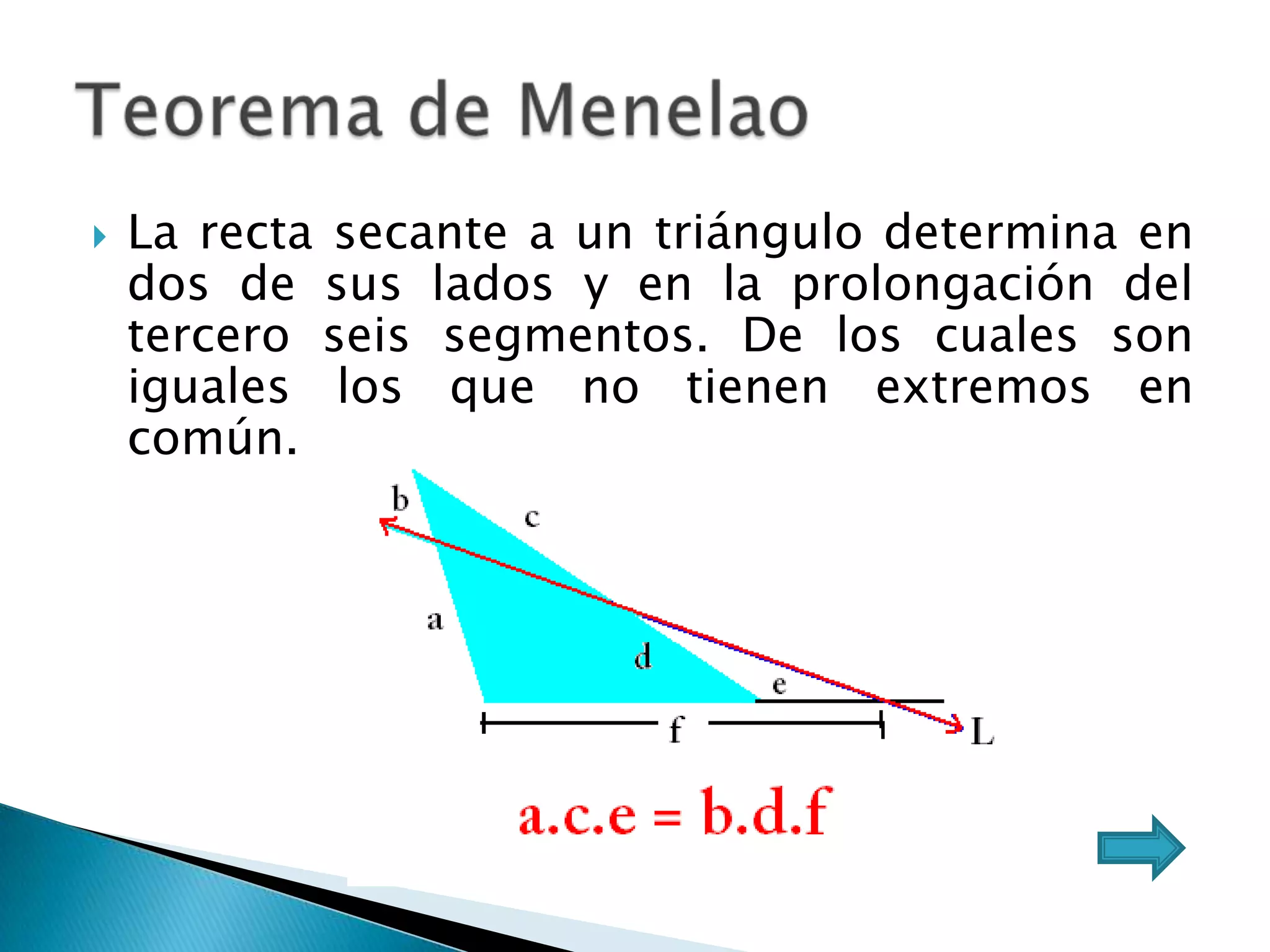
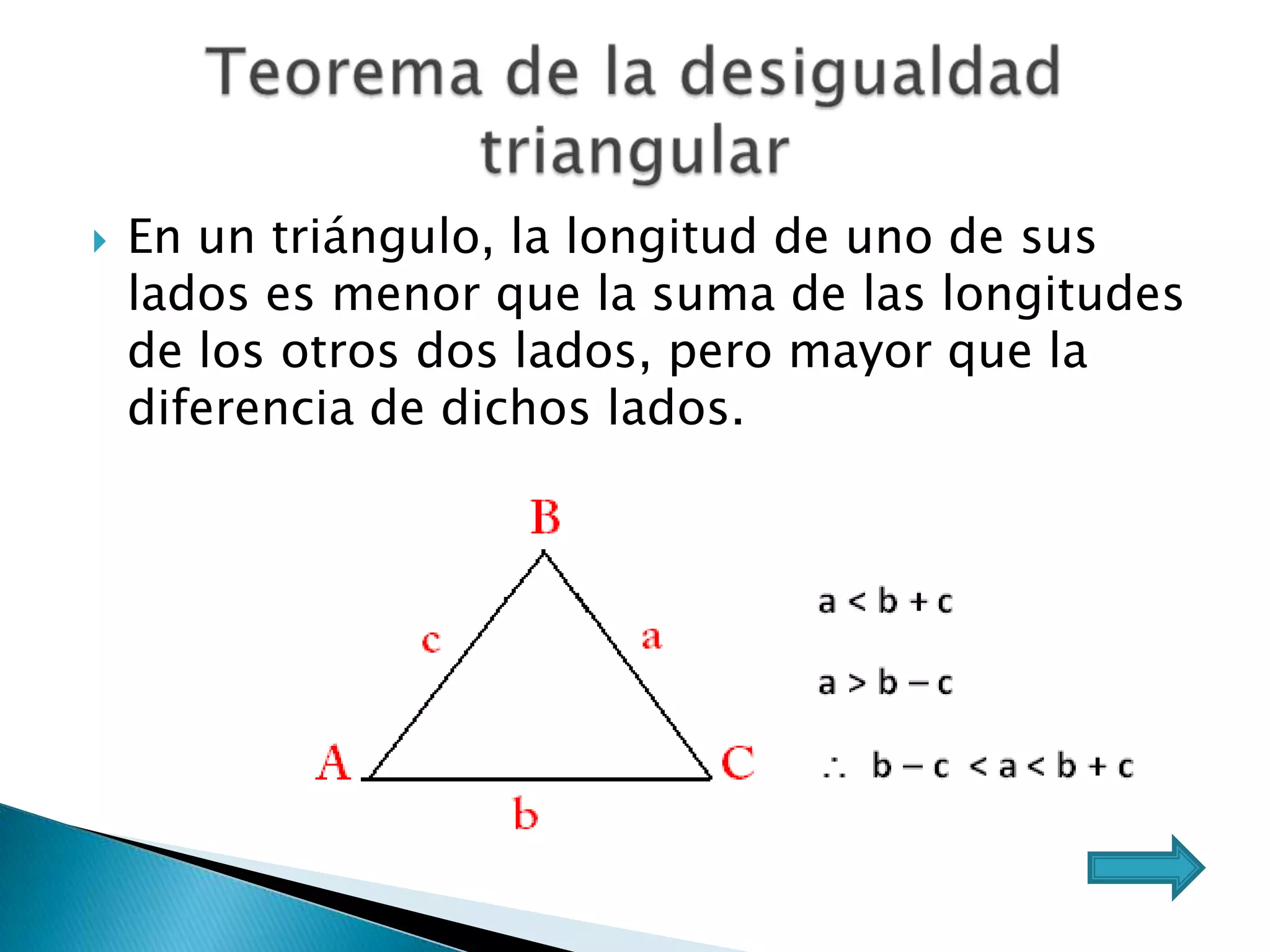
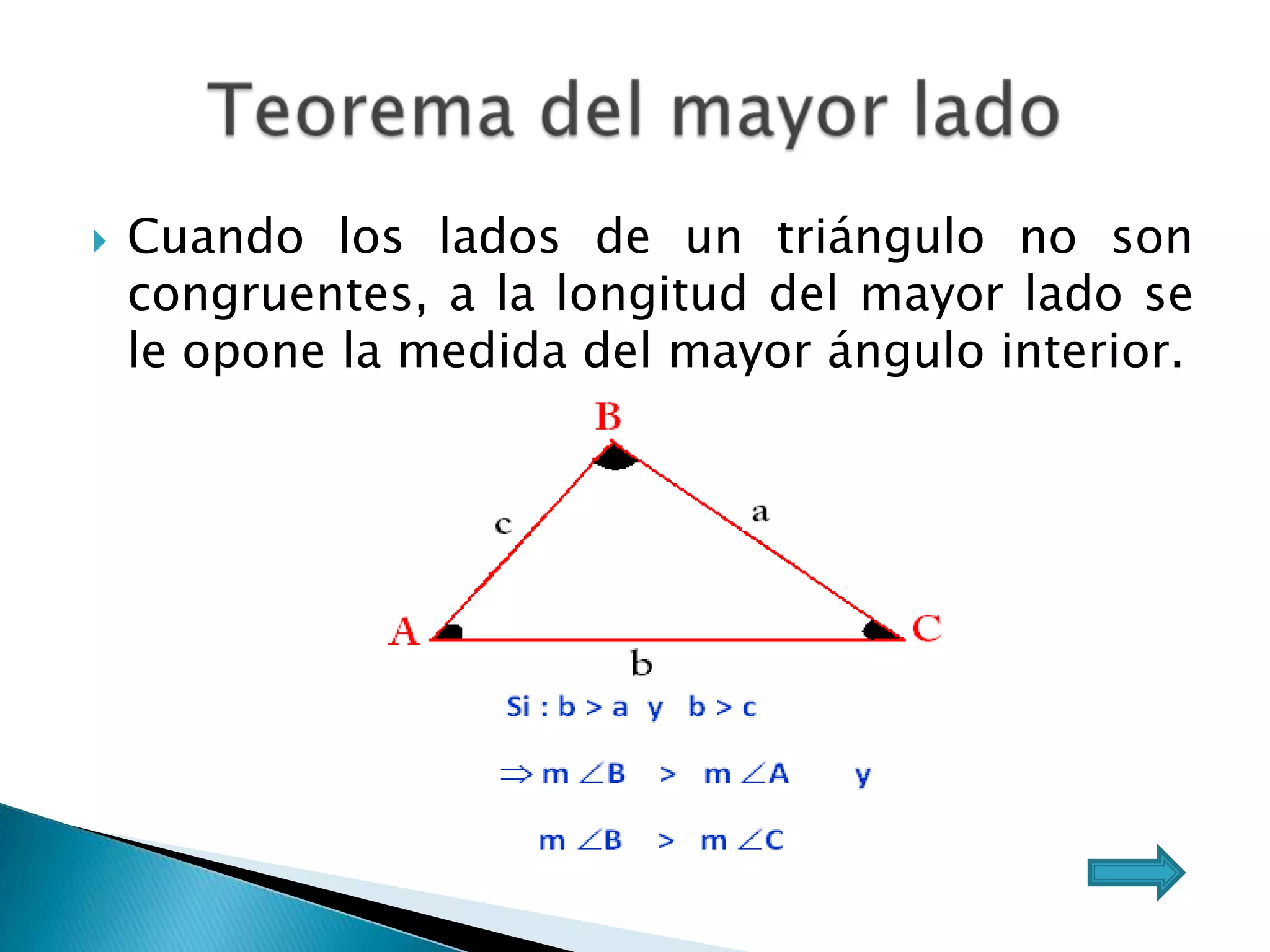
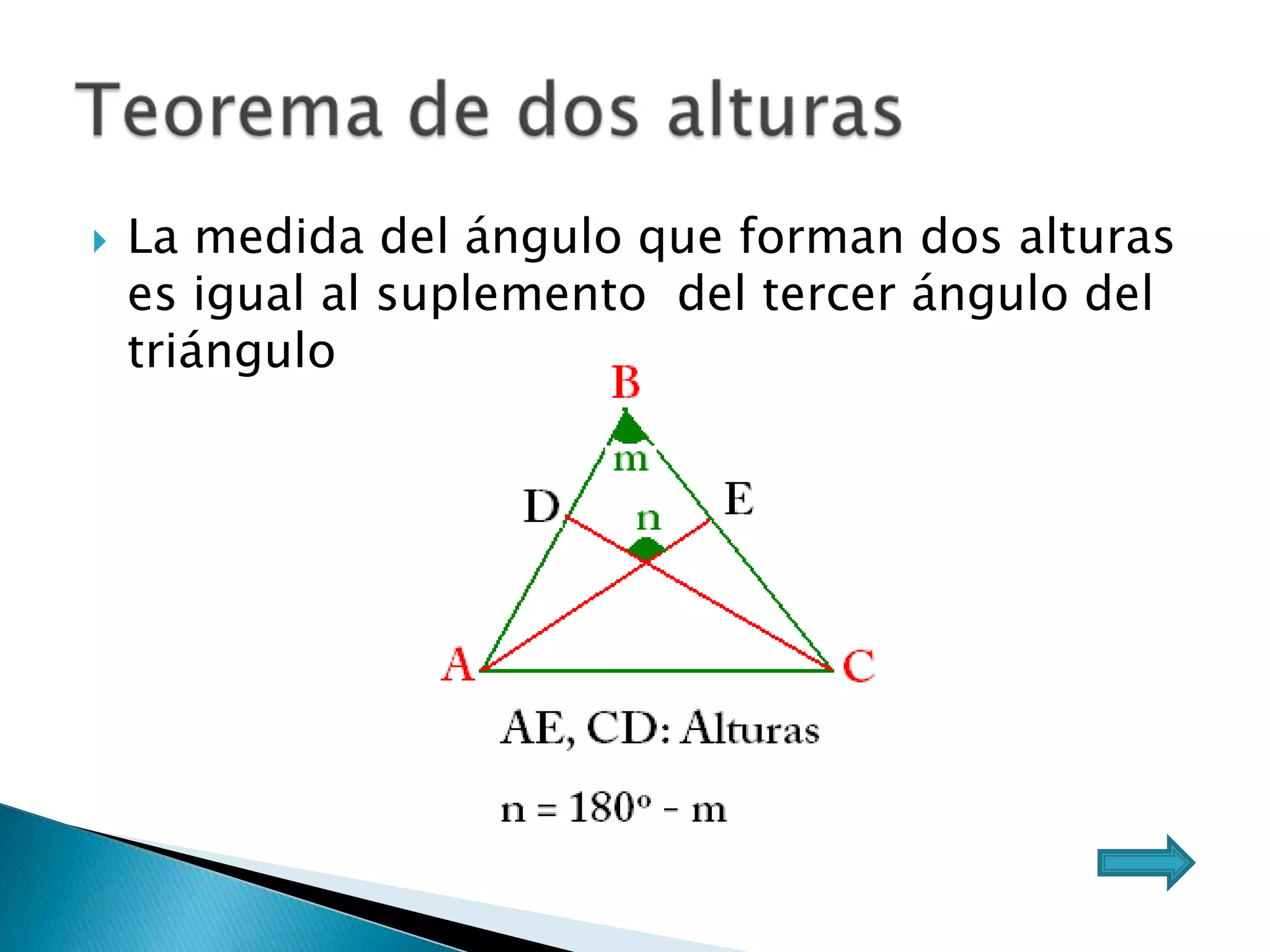
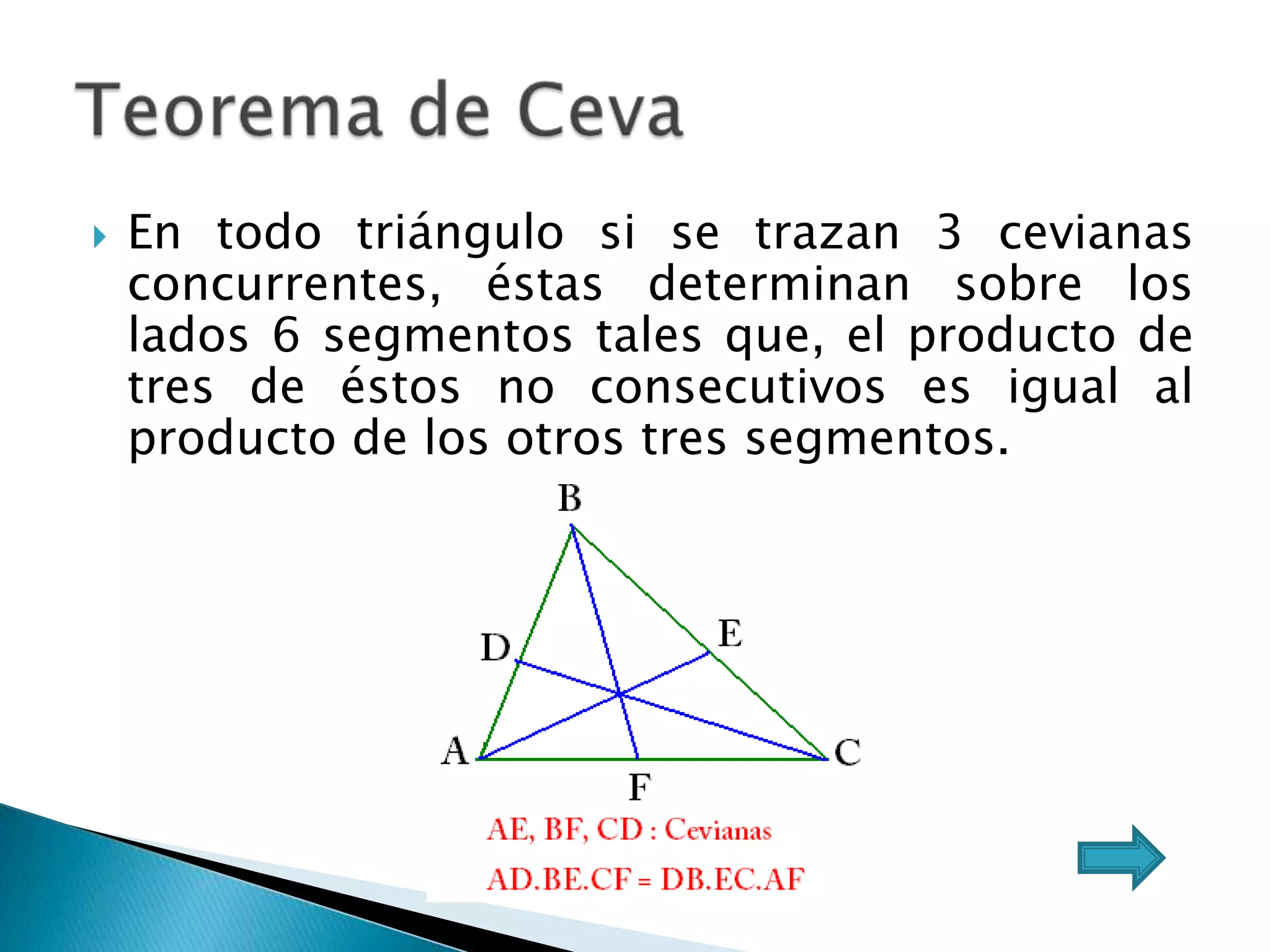
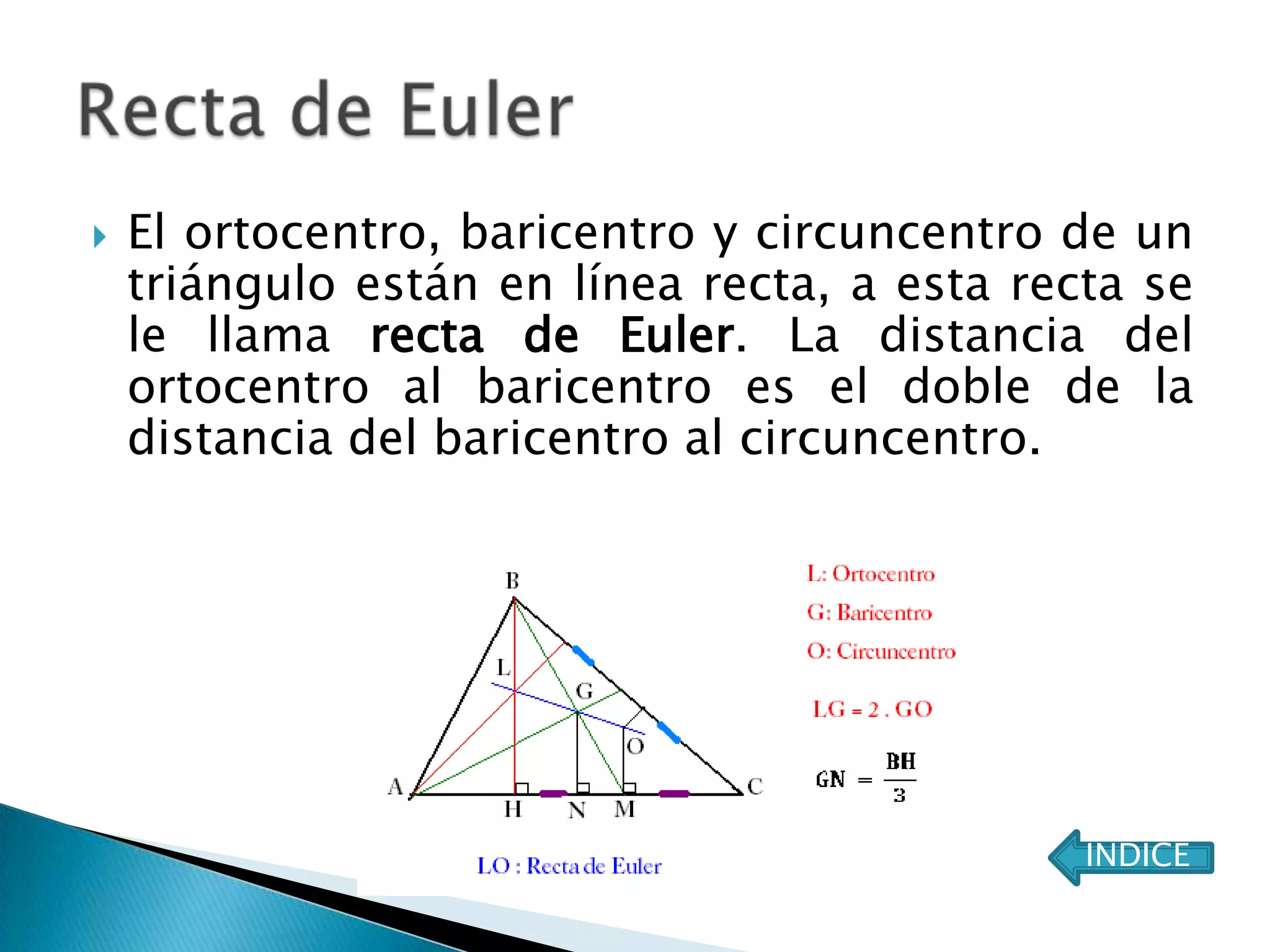
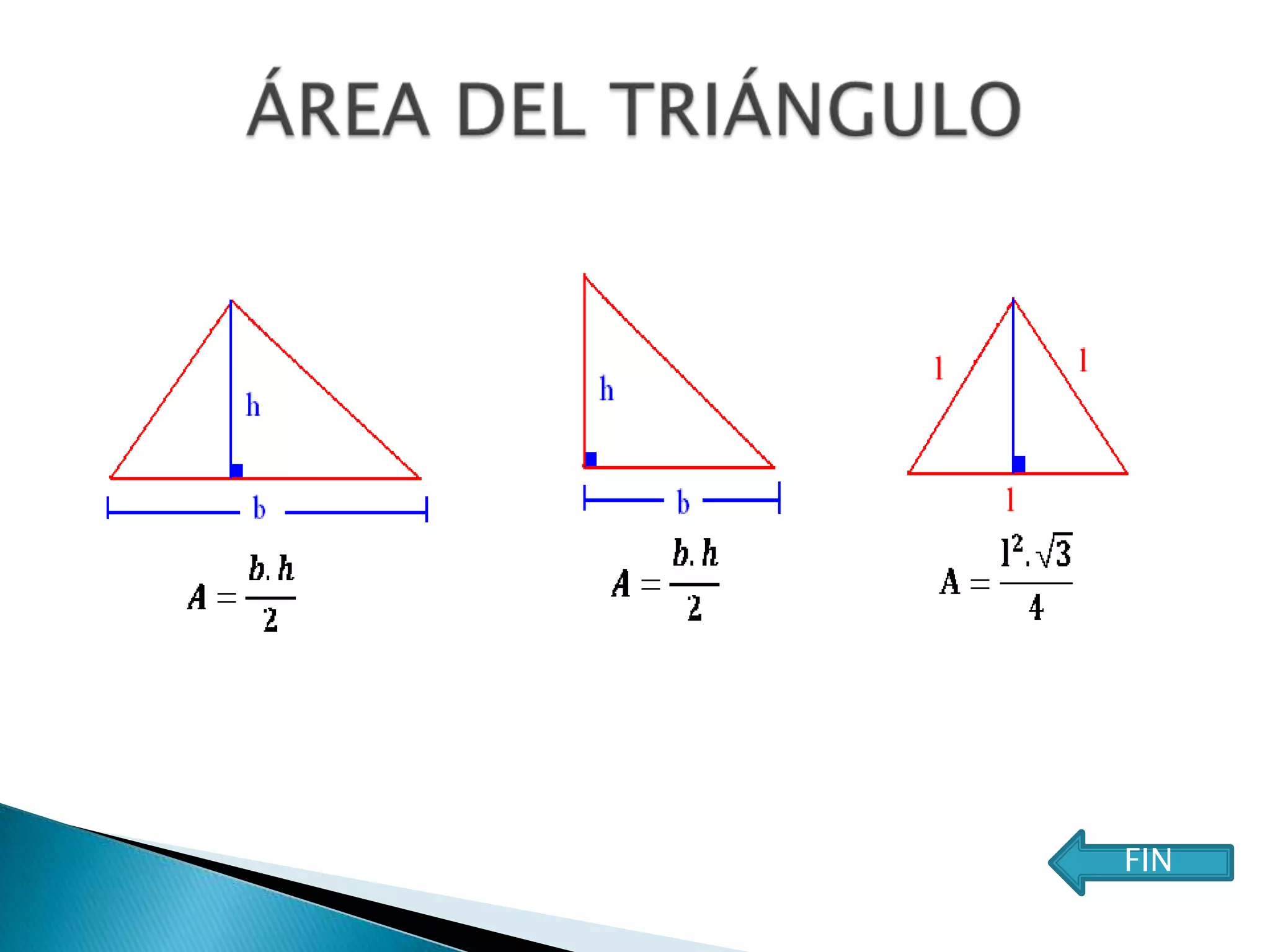
Este documento presenta varios teoremas fundamentales sobre triángulos, incluyendo la semejanza, congruencia y propiedades de triángulos notables. Explica que dos triángulos son semejantes si tienen dos ángulos interiores congruentes o lados proporcionales, y congruentes si tienen lados congruentes. También cubre teoremas sobre ángulos, lados, alturas y otras características geométricas de triángulos.

1. POR : ELADIA FLORES

2.  Semejanza de triángulos
 Congruencia de triángulos
 Otros teoremas fundamentales
 Triángulos notables
 Área del triángulo

3. Primer caso:
Dos triángulos son semejantes si tienen dos
pares de ángulos interiores congruentes

4.  Dos triángulos son semejantes si tienen un
par de ángulos interiores congruentes y los
lados que los forman respectivamente
proporcionales

5.  Dos triángulos son semejantes si los tres
pares de lados son proporcionales.

6.  Si dos triángulos son semejantes también son
proporcionales lo perímetros, las alturas, las
medianas y las bisectrices.

7.  Si trazamos la recta L secante a un triángulo
ABC y paralela a uno de sus lados, se forma
un triángulo parcial semejante al triángulo
ABC
INDICE

8.  Dos triángulos son congruentes, cuando
tienen sus lados congruentes tomados de dos
en dos.

9. ÍNDICE

10. Otros teoremas

13.  En todo triángulo rectángulo, la suma de
longitudes de los catetos es igual a la suma
de las longitudes de la hipotenusa y el
diámetro.

14.  Los lados adyacentes a una bisectriz interior
son proporcionales a los segmentos que
determina en el tercer lado del triángulo.

15.  Los lados adyacentes a una bisectriz exterior
son proporcionales a los segmentos que
determina en la prolongación del tercer lado
del triángulo.

16.  El incentro determina en la bisectriz
segmentos proporcionales a la suma de los
lados adyacentes y el tercer lado.

17.  En todo triángulo, para el cálculo de una de
las alturas, se emplea la siguiente relación:
donde hb representa a la longitud de la
relativa a b y p es semiperímetro del triángulo

18.  En todo triángulo , la suma de los cuadrados
de dos lados es igual al doble del cuadrado
de la mediana relativa al tercer lado mas la
mitad del cuadrado de dicho lado.

19.  La recta secante a un triángulo determina en
dos de sus lados y en la prolongación del
tercero seis segmentos. De los cuales son
iguales los que no tienen extremos en
común.

20.  En un triángulo, la longitud de uno de sus
lados es menor que la suma de las longitudes
de los otros dos lados, pero mayor que la
diferencia de dichos lados.

21.  Cuando los lados de un triángulo no son
congruentes, a la longitud del mayor lado se
le opone la medida del mayor ángulo interior.

22.  Los ángulos agudos de un triángulo
rectángulo son complementarios
 Los ángulos agudos de un triángulo
rectángulo isósceles miden 45º cada uno
 La medida de un ángulo exterior es mayor
que cualquiera de las medidas de los ángulos
interiores que no le son adyacentes
 A la longitud del menor lado se le opone la
medida del menor ángulo interior
 Al mayor lado le corresponde la menor
altura, mediana, bisectriz

23.  La medida del ángulo que forman dos alturas
es igual al suplemento del tercer ángulo del
triángulo

24.  En todo triángulo si se trazan 3 cevianas
concurrentes, éstas determinan sobre los
lados 6 segmentos tales que, el producto de
tres de éstos no consecutivos es igual al
producto de los otros tres segmentos.

25.  El ortocentro, baricentro y circuncentro de un
triángulo están en línea recta, a esta recta se
le llama recta de Euler. La distancia del
ortocentro al baricentro es el doble de la
distancia del baricentro al circuncentro.
ÍNDICE

26. ÍNDICE

27. FIN