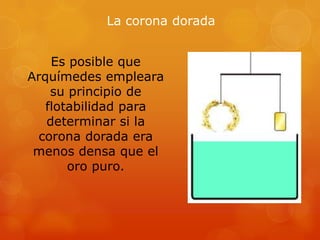
Este documento describe el trabajo del científico griego Arquímedes en hidrostática. Explica cómo Arquímedes descubrió el principio de flotación y cómo lo usó para determinar si la corona de un rey estaba hecha de oro puro. También cubre otros logros matemáticos y de ingeniería de Arquímedes y las circunstancias de su muerte.

1. Centro de Bachillerato Tecnológico Industrial y de
Servicios CBTIS no.140
“Hermila Galindo de Topete”
El principio fundamental de la Hidrostática
Científico que lo Realizo: Arquímedes de Siracusa
Año:530 d. C.
Profa:Profa. Ocean. Ma. Elena Sosa Medina
Integrantes del Equipo:
Rubio Colis Edson Adrián
Vera Sosa Brandon

2. Arquímedes de Siracusa
fue un matemático griego, físico, ingeniero, inventor y
astrónomo. Aunque se conocen pocos detalles de su
vida, es considerado uno de los científicos más
importantes de la antigüedad clásica. Entre sus
avances en física se encuentran sus fundamentos en
hidrostática, estática y la explicación del principio de
la palanca. Es reconocido por haber diseñado
innovadoras máquinas, incluyendo armas de asedio y
el tornillo de Arquímedes, que lleva su nombre.
Experimentos modernos han probado las afirmaciones
de que Arquímedes llegó a diseñar máquinas capaces
de sacar barcos enemigos del agua o prenderles fuego
utilizando una serie de espejos.

4. Se considera que Arquímedes fue uno de
los matemáticos más grandes de la
antigüedad y, en general, de toda la
historia. Usó el método exhaustivo para
calcular el área bajo el arco de una
parábola con el sumatorio de una serie
infinita, y dio una aproximación
extremadamente precisa del número Pi.
También definió la espiral que lleva su
nombre, fórmulas para los volúmenes de
las superficies de revolución y un
ingenioso sistema para expresar números
muy largos.

6. A diferencia de sus inventos, los escritos
matemáticos de Arquímedes no fueron muy
conocidos en la antigüedad. Los matemáticos de
Alejandría lo leyeron y lo citaron, pero la primera
compilación integral de su obra no fue realizada
hasta c. 530 d. C. por Isidoro de Mileto. Los
comentarios de las obras de Arquímedes escritas
por Eutocio en el siglo VI las abrieron por primera
vez a un público más amplio. Las relativamente
pocas copias de trabajos escritos de Arquímedes
que sobrevivieron a través de la Edad Media fueron
una importante fuente de ideas durante el
Renacimiento, mientras que el descubrimiento en
1906 de trabajos desconocidos de Arquímedes en el
Palimpsesto de Arquímedes ha ayudado a
comprender cómo obtuvo sus resultados
matemáticos.

7. LA
C
O
R
O D
N O
A R
A
D
A

8. Una de las anécdotas
más conocidas sobre Arquímedes tenía que
Arquímedes cuenta cómo resolver el problema sin
inventó un método para dañar la corona, así que
determinar el volumen no podía fundirla y
de un objeto con una convertirla en un cuerpo
forma irregular. De regular para calcular su
acuerdo con masa y volumen, a partir
Vitruvio, Hierón II
de ahí, su densidad.
ordenó la fabricación de
Mientras tomaba un
una nueva corona con
baño, notó que el nivel
forma de corona
triunfal, y le pidió a
de agua subía en la
Arquímedes determinar bañera cuando entraba, y
si la corona estaba hecha así se dio cuenta de que
sólo de oro o si, por el ese efecto podría ser
contrario, un orfebre usado para determinar el
deshonesto le había volumen de la corona.
agregado plata en su
realización.

9. Debido a que el agua no se puede comprimir, la
corona, al ser sumergida, desplazaría una cantidad de
agua igual a su propio volumen. Al dividir el peso de
la corona por el volumen de agua desplazada se
podría obtener la densidad de la corona. La densidad
de la corona sería menor que la densidad del oro si
otros metales menos densos le hubieran sido
añadidos.

10. Cuando Arquímedes, durante el baño, se dio cuenta del
descubrimiento, se dice que salió corriendo desnudo por las calles, y
que estaba tan emocionado por su hallazgo que olvidó vestirse. Según
el relato, en la calle gritaba "¡Eureka!" (en griego antiguo: "εὕρηκα"
que significa "¡Lo he encontrado!") Sin embargo, la historia de la
corona dorada no aparece en los trabajos conocidos de Arquímedes.
Además, se ha dudado que el método que describe la historia fuera
factible, debido a que habría requerido un nivel de exactitud extremo
para medir el volumen de agua desplazada.

11. La corona dorada
Es posible que
Arquímedes empleara
su principio de
flotabilidad para
determinar si la
corona dorada era
menos densa que el
oro puro.

12. En lugar de esto, Usando este principio, habría
Arquímedes podría haber s i d o p o s i b l e
buscado una solución en c o mp a r a r l a
la que aplicaba el d e n s i d a d d e l a
principio de la corona dorada con la de oro
hidrostática conocido puro al usar una balanza.
como el principio de Situando en un lado de la
Arquímedes, descrito en balanza la corona objeto de la
investigación y en el otro una
su tratado Sobre los
muestra de oro puro del mismo
cuerpos flotantes. Este
peso, se procedería a sumergir la
principio plantea que todo balanza en el agua; si la corona
cuerpo sumergido en un tuviese menos densidad que el
líquido experimenta un oro, desplazaría más agua debido
empuje de abajo hacia a su mayor volumen y
arriba igual al peso del experimentaría un mayor empuje
líquido que la muestra de oro. Esta
d e s a l o j a d o . diferencia de flotabilidad
inclinaría l a b a l a n z a

13. EL RAYO DE CALOR DE ARQUÍMEDES, ¿MITO O REALIDAD?
Según la tradición, dentro Luciano de Samosata,
de sus trabajos en la historiador también del siglo
II, escribió que, durante el
defensa de sitio de Siracusa (213-211 a.
Siracusa, Arquímedes C.), Arquímedes repelió un
podría haber creado un ataque llevado a cabo por
sistema de espejos ustorios soldados romanos con fuego.
Siglos más tarde, Antemio de
que reflejaban la luz solar Tralles menciona los espejos
concentrándola en los ustorios como arma utilizada
barcos enemigos y con la por Arquímedes. El artefacto,
finalidad de incendiarlos. que en ocasiones es
denominado como el "rayo de
Sin embargo, las fuentes calor de Arquímedes", habría
que recogen estos hechos servido para enfocar la luz
son tardías, siendo la solar en los barcos que se
primera de ellas Galeno, ya acercaban, haciendo que estos
ardieran.
en el siglo II.

14. La credibilidad de esta historia
ha sido objeto de debate
desde el Renacimiento. René
Descartes la rechazó como
falsa, mientras que
investigadores modernos han
intentado recrear el efecto
considerando para ello tan sólo
las capacidades técnicas de las
que disponía Arquímedes. Se
ha sugerido que una gran
cantidad de escudos bien
pulidos de bronce o cobre
podrían haber sido utilizados
como espejos, para así enfocar
la luz solar hacia un solo
barco. De este modo se habría
podido utilizar el principio del
reflector parabólico, en una
manera similar a un horno
solar.

15. Por experiencia sabemos que los cuerpos pesan menos cuando
están sumergidos en un líquido, esto se debe a que el fluido
(con los gases también ocurre) ejerce sobre el cuerpo una
fuerza hacia arriba que llamamos empuje.
Arquímedes (s. III a.C.) fue el primero en darse cuenta de este
empuje y además calculó a cuánto equivalía éste, el principio de
Arquímedes dice que cuando un cuerpo se encuentra sumergido
en un fluido experimenta una fuerza hacia arriba, llamada
empuje, igual al peso del fluido que ha desalojado.
Calculemos el peso del fluido desalojado, éste será igual a la
masa desalojada multiplicada por la aceleración de la gravedad
y a su vez esta masa será igual al volumen de fluido desalojado
(volumen del cuerpo que está sumergido) por la densidad de
éste:
E = Pesodesalojado = mdes• g = dfluido • Vsumergido • g

16. El Principio Fundamental de la Hidrostática
establece que si nos sumergimos en un
fluido (líquido o gas), la presión ejercida por
éste es proporcional a la profundidad a que
nos encontremos:
P=d.g.h
Donde:
d = densidad del fluido (en kg/m3)
g = aceleración de la gravedad (m/s2)
h = distancia del punto a la superficie (m)

17. hidrostática

18. Arquímedes fue asesinado al final del asedio
por un soldado romano, contraviniendo las
órdenes del general romano, Marcelo, de
respetar la vida del gran matemático griego.
Existen diversas versiones de la muerte de
Arquímedes: Plutarco, en su relato, nos da
hasta tres versiones diferentes. De acuerdo
con su relato más popular, Arquímedes
estaba contemplando un diagrama
matemático cuando la ciudad fue tomada.
Un soldado romano le ordenó ir a
encontrarse con el General, pero
Arquímedes hizo caso omiso a esto, diciendo
que tenía que resolver antes el problema. El
soldado, enfurecido ante la respuesta, mató
a Arquímedes con su espada.