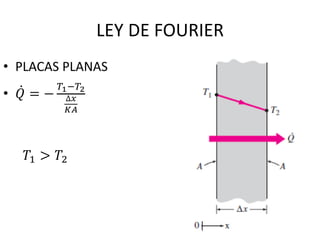
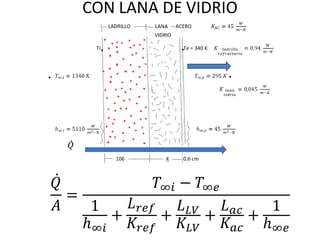
El documento aborda la transferencia de calor y masa, discutiendo conceptos fundamentales como la energía en tránsito, las leyes de la termodinámica, y mecanismos de transferencia como conducción, convección y radiación. Se incluye una explicación detallada de las leyes de Fourier y Newton, así como problemas prácticos que ilustran la aplicación de estos principios en sistemas térmicos. Además, se ofrecen fórmulas y ejemplos para calcular la transferencia de calor en diversas configuraciones de materiales y condiciones.