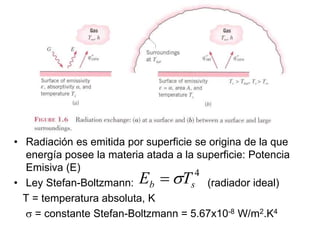
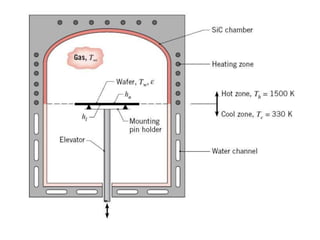
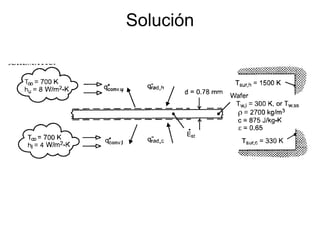
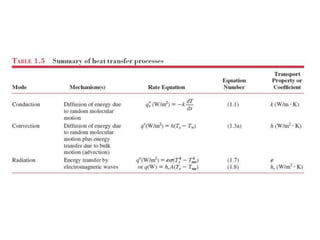
El documento trata sobre la transferencia de calor. Brevemente explica que (1) la transferencia de calor estudia la transferencia de energía entre cuerpos debido a una diferencia de temperatura, (2) los mecanismos principales de transferencia de calor son la conducción, convección, radiación y cambio de fase, y (3) la transferencia de calor predice cómo varían las temperaturas con el tiempo hasta alcanzar el equilibrio, mientras que la termodinámica solo predice la temperatura final de equilibrio.

1. Transferencia de Calor
Teófilo Donaires Flores
Departamento de Ingeniería Química

2. Transferencia de Calor
• Ciencia que estudia la transferencia de energía
que toma lugar entre cuerpos, materiales, fluidos,
en vacío como resultado de una diferencia en
temperatura:
• q α ΔT
• Termodinámica:
– dice que la energía es transferida por una diferencia en
temperatura se conoce como calor. Calor es una
forma de energía en transito, ocurre si existe una dif. en
temp. La termodinámica brega con sistemas en
equilibrio, no dice con que rapidez ocurre el intercambio
entre estados de equilibrio.

3. • ejemplo: barra de acero caliente que se sumerge en
un volumen dado de agua fría.
• solución Termodinámica: predice la temperatura de
equilibrio final de ambos cuerpos.
ΔHH2O + ΔHacero = Q - W = 0
• mH2OCpH2O (Te - TH20, i) + macero Cpacero (Tacero, i -Te) = 0,
determinar Te.
• Transferencia de calor: predice como ambas
temperaturas varían con el tiempo hasta
llegar a la temperatura de equilibrio:
TH20 = f(t), Tacero = f(t).

4. Mecanismos o modos de TC
• Conducción
– Cuando existe gradiente en temp. en medio (sólido,
líquido, gas) estacionario
• Convección
– Entre superficie y fluido moviéndose
• Convección forzada
• Convección natural
• Ebullición
• Condensación
• Radiación
– Toda superficie a temp. dada emite energía en forma
ondas electromagnética (puede haber ausencia de
medio)

5. Fig 1.1

6. Conducción
• TC en medio estacionario
• Gases
– Transferencia energía de partículas más
energética a menos energética de una
sustancia debido a interacciones de las
partículas
– energía asociada a movimiento al azar de
translación, rotacional interna y movimiento
vibracional de las moléculas

7. Conducción
• Líquidos
– Moléculas están mas cerca y las interacciones
moleculares son más fuertes y frecuentes
• Sólidos
– Conducción atribuye a actividad atómica en
forma de vibraciones látices

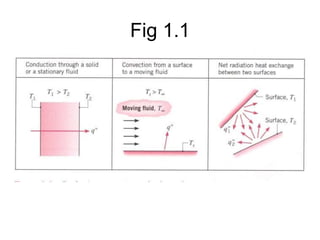
8. Conducción
• Ley Fourier (estado
estacionario)
k = conductividad térmica
del medio [W/m.K]
T1
T2
T(x)
A
L
x
T
qx
”  





 






 


















L
T
T
k
L
T
T
k
q
L
T
T
dx
dT
W
dx
dT
kA
q
m
W
dx
dT
k
q
x
x
x
2
1
1
2
1
2
2
,
,

9. Ejemplo
• Las temperaturas superficiales interna y
externa de una ventana de vidrio son 15 y
5oC. La ventana tiene las dimensiones de
1 m por 3 m y 5 mm de grosor. La
conductividad térmica del vidrio es 1.4
W/m.K

10. Solución Ejemplo
Ti=15oC
To = 5oC
3 m
1 m
5 mm
k = 1.4 W/m.oC
 
 
W
q
m
C
m
C
m
W
q
m
mm
x
m
m
m
W
H
A
x
T
T
kA
dx
dT
kA
q
o
o
i
o
8400
005
.
0
15
5
3
.
4
.
1
005
.
0
5
3
)
1
)(
3
(
.
2
2








 















11. Convección
• Transferencia de superficie a fluido
• Mecanismos
– Natural o libre
• Movimiento molecular al azar por diferencia en
densidad del fluido
• Inducido por fuerzas boyantes
– Forzado
• movimiento del fluido por metodos externos
(abanico, bomba, viento atmosférico
– Ebullición
– Condensación

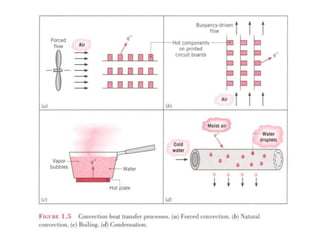
13. Convección
• Fig. 1.4
• Ley de Newton
h = coeficiente de
transferencia de calor por
convección, [W/m2.K]
– Depende condiciones capa
limite, geometría superficie,
naturaleza de movimiento
fluido, propiedades
termodinámicas y de
transporte del fluido
 
 








T
T
hA
q
T
T
h
q
s
s

14. Valores Típicos de h
Proceso h, [W/m2.K]
Convección Libre
Gases 2 - 25
Líquidos 50 - 1000
Convección Forzada
Gases 25 - 250
Líquido 50 – 20,000
Convección con cambio de
fase:
Ebullición o condensación 2500 – 100,000

15. Ejemplo
• Un “chip” cuadrado isotérmico de 5 mm,
superficie esta montado en un substrato tal que
la superficie de atrás y laterales esta bien
aislada, mientras la superficie frontal esta
expuesta a un flujo de un enfriante a T∞ = 15oC.
Por consideraciones de reliabilidad la
temperatura del chip no puede exceder de 85oC.
Si el agente enfriante es aire y h = 200 W/m2.K,
?cual es la potencia máxima permisible del chip?
• Sí el enfriante es un líquido dieléctrico donde h =
3000 W/m2.K, ?Cual es la potencia máxima
permisible del chip?

16. Solución Ejemplo
Ts ≤ 85oC
Enfriante
T∞ = 15oC , h
w = 5 mm
   
    W
x
q
W
x
q
C
m
W
h
C
m
W
h
C
T
C
T
m
x
A
T
T
hA
q
o
o
o
o
s
s
25
.
5
)
15
85
10
5
.
2
3000
35
.
0
)
15
85
10
5
.
2
200
.
/
3000
,
.
/
200
15
,
85
10
5
.
2
)
005
.
0
(
)
(
5
max
,
2
5
max
,
1
2
2
2
1
2
5
2






















17. Radiación
• Radiación térmica
– Energía emitida por materia que esta a una
temperatura diferente de cero
– Emisión puede ser de superficie sólida, pero
también de líquidos y gases
– Energía transportada por ondas
electromagnéticas
– No es necesaria la presencia de materia para
transferirse
• Es más eficiente en vacío

18. • Radiación es emitida por superficie se origina de la que
energía posee la materia atada a la superficie: Potencia
Emisiva (E)
• Ley Stefan-Boltzmann: (radiador ideal)
T = temperatura absoluta, K
 = constante Stefan-Boltzmann = 5.67x10-8 W/m2.K4
4
s
b T
E 


19. • Para superficie real la energía emitida es menor
que radiador ideal (cuerpo negro):
 = emisividad superficie (propiedad radiactiva de la
superficie (0    1)
• Una porción de la irradiación puede se absorbida
aumentado la energía térmica del material:
 = absorptividad (0    1)
• si  < 1 y superficie es opaca una porción de la
irradiación es reflejada
• Si superficie es semi-transparente una porción de
la irradiación puede ser trasmitida
4
s
T
E 

G
Gabs 


20. • Caso que ocurre frecuentemente:
– intercambio de radiación entre una superficie pequeña a
Ts y superficie mucho más grande (paredes del salón o u
horno) a Tsurr
• Para caso superficie gris:  = , la razón neta de
calor transferido por radiación es:
hr = coeficiente TC por radiación
 
 
  
2
2
4
4
(
)
(
surr
s
surr
s
r
surr
s
r
rad
surr
s
s
b
rad
T
T
T
T
h
T
T
A
h
q
T
T
G
T
E
A
q
q

















21. • Caso de superficie donde calor por conducción es
transferido por convección y radiación:
Balance energía:
qcond - qconv - qrad = 0: qcond = qconv + qrad
- kA(dT/dx) = hA(Ts - T) + A(Ts
4 – Tsurr
4)
A Ts
h, T
Tsurr
qrad
qconv
qcond

22. Problema 1.26
• Cámara simulación para probar paquete de
instrumentación que tiene una superficie
esférica externa de D = 100 mm y  = 0.25
• Temperatura superficie cámara se mantiene a
77 K.
• Temperatura superficie paquete debe
mantenerse: 40 ≤ Ts ≤ 850C
• Determinar el rango de disipación de potencia
aceptable para el paquete y el efecto de
variación de valor emisividad: 0.20 y 0.30

24. Solución
 
 
:
85
40
:
3
.
4
77
313
)
10
67
.
5
)(
10
.
0
(
25
.
0
:
313
273
40
40
4
4
8
2
4
4
C
T
para
similares
nes
Calculacio
W
x
x
P
q
K
C
T
Cuando
T
T
A
P
q
o
s
e
rad
o
s
sur
s
s
e
rad


















25. Prob. 1.43
Datos: Horno procesar materiales semi-conductores formado
por cámara de silicon-carbide
Th = 1500 K, Tc = 330 K,  = 0.65, d = 0.78 mm, T∞ = 700 K =
Tsurr, hu = 8 W/m2.K, hl = 4 W/m2.K,  = 2700 kg/m3, cp =
875 J/kg.K
Determinar:
a) Para condición inicial de temperatura de un wafer y la
posición del wafer mostrado esquematicamente,
determinar la razón de cambio en temperatura con
tiempo: (dTw/dt)I
b) Determinar la temperatura alcanzada a condiciones
estacionarias y ?cuan significante es el calor transferido
por convección para esta situación?

27. Solución

28. Solución
       
s
K
dt
dT
dt
dT
x
x
K
T
T
t
inicial
Condición
a
dt
dT
c
T
T
h
T
T
h
T
T
T
T
dt
dT
c
q
q
q
q
E
E
E
i
w
i
w
i
w
w
w
w
w
u
w
c
sur
w
h
sur
w
conv
u
conv
c
rad
h
rad
std
out
in
104
)
00078
.
0
)(
875
(
2000
)
700
300
(
4
)
700
300
(
8
)
300
330
)(
10
67
.
5
(
65
.
0
)
300
1500
)(
10
67
.
5
(
65
.
0
300
,
0
:
)
(
4
4
8
4
4
8
,
1
4
4
,
4
4
,
1
,
,
,
,






















































 






29.    
ss
w
i
w
ss
w
i
w
ss
w
ss
w
ss
w
ss
w
ss
w
ss
w
w
T
y
dt
dT
controla
radiación
por
ercambio
de
proceso
conclusión
K
T
s
K
dt
dT
convección
de
efectos
los
ignoramos
Si
K
T
T
T
T
T
T
T
Acc
ias
Estacionar
s
Condicione
,
,
,
,
,
4
,
4
4
,
4
,
:
int
:
1262
,
101
:
1251
0
700
4
700
8
)
330
(
65
.
0
)
1500
(
65
.
0
0
:


























