Este documento presenta un libro sobre fundamentos de programación orientada a objetos aplicada a estructuras de datos en Java. El libro introduce conceptos clave de POO como objetos, clases, herencia, polimorfismo y encapsulamiento. Luego cubre implementaciones de estructuras de datos comunes como pilas, colas, listas enlazadas y árboles binarios utilizando el paradigma de POO en Java. El libro busca proporcionar una comprensión sólida de POO y estructuras de datos a través de ejemplos prácticos es

2. Fundamentos de la Programación Orientada a
Objetos
Una Aplicación a las Estructuras de Datos en
JavaTM
Ricardo Ruiz Rodrı́guez
Universidad Tecnológica de la Mixteca
Instituto de Computación

4. A Thelma

5. Ruiz Rodríguez, Ricardo
Fundamentos de la programación orientada a objetos: una aplicación a las estructuras de
datos en Java - 1º ed. - El Cid Editor, 2014.
pdf
ISBN digital – pdf 978-1-4135-2433-8
Fecha de catalogación: 18/02/2014
© Ricardo Ruiz Rodríguez
© El Cid Editor
ISBN versión digital pdf: 978-1-4135-2433-8

6. Índice general
Índice de figuras ix
Índice de ejemplos xiii
Prefacio xvii
1. Orientación a Objetos 1
1.1. Orı́genes . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 1
1.2. Paradigma . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 2
1.2.1. Una perspectiva diferente . . . . . . . . . . . . . . . . 4
1.2.2. Objetos . . . . . . . . . . . . . . . . . . . . . . . . . . 5
1.2.3. Objetos y clases . . . . . . . . . . . . . . . . . . . . . . 6
1.3. Orientación a objetos y modularidad . . . . . . . . . . . . . . 8
1.3.1. Cohesión y Acoplamiento . . . . . . . . . . . . . . . . 9
1.4. Caracterı́sticas fundamentales de la POO . . . . . . . . . . . . 9
1.5. Consideraciones finales . . . . . . . . . . . . . . . . . . . . . . 12
1.6. Ejercicios . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 13
2. Programación Orientada a Objetos 15
2.1. Mensajes y métodos . . . . . . . . . . . . . . . . . . . . . . . 16
2.1.1. Métodos sin argumentos . . . . . . . . . . . . . . . . . 16
2.1.2. Métodos con argumentos . . . . . . . . . . . . . . . . . 17
2.1.3. Métodos y atributos . . . . . . . . . . . . . . . . . . . 19
2.1.4. Métodos y constructores . . . . . . . . . . . . . . . . . 21
2.1.5. Sobrecarga . . . . . . . . . . . . . . . . . . . . . . . . . 23
2.2. Herencia . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 25
2.2.1. Abstracción . . . . . . . . . . . . . . . . . . . . . . . . 25
2.2.2. Implementación . . . . . . . . . . . . . . . . . . . . . . 28
v

7. ÍNDICE GENERAL
2.3. Consideraciones finales . . . . . . . . . . . . . . . . . . . . . . 33
2.3.1. Respecto al envı́o de mensajes . . . . . . . . . . . . . . 33
2.3.2. Respecto a la sobrecarga de operadores . . . . . . . . . 33
2.3.3. Respecto al paradigma . . . . . . . . . . . . . . . . . . 33
2.4. Ejercicios . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 35
3. Estructuras de datos 39
3.1. Panorama general . . . . . . . . . . . . . . . . . . . . . . . . . 39
3.2. Tipos de datos y referencias . . . . . . . . . . . . . . . . . . . 40
3.3. Tipos de datos abstractos (ADT) . . . . . . . . . . . . . . . . 41
3.3.1. Especificación del ADT Racional . . . . . . . . . . . . 43
3.3.2. Implementación del ADT Racional . . . . . . . . . . . 44
3.4. Abstracción de estructuras de datos . . . . . . . . . . . . . . . 47
3.4.1. Clases autorreferidas . . . . . . . . . . . . . . . . . . . 48
3.4.2. Implementación . . . . . . . . . . . . . . . . . . . . . . 50
3.5. Consideraciones finales . . . . . . . . . . . . . . . . . . . . . . 50
3.6. Ejercicios . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 52
4. Pilas 55
4.1. Definición . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 55
4.1.1. Operaciones primitivas . . . . . . . . . . . . . . . . . . 56
4.2. Implementación . . . . . . . . . . . . . . . . . . . . . . . . . . 57
4.2.1. Pila primitiva . . . . . . . . . . . . . . . . . . . . . . . 57
4.2.2. Pila genérica . . . . . . . . . . . . . . . . . . . . . . . 63
4.3. Aplicaciones . . . . . . . . . . . . . . . . . . . . . . . . . . . . 66
4.3.1. Análisis básico de expresiones . . . . . . . . . . . . . . 66
4.3.2. Notación interfija, postfija y prefija . . . . . . . . . . . 69
4.3.3. Evaluación de expresiones . . . . . . . . . . . . . . . . 71
4.4. Consideraciones finales . . . . . . . . . . . . . . . . . . . . . . 72
4.5. Ejercicios . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 74
5. Colas de espera 79
5.1. Definición . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 79
5.1.1. Operaciones primitivas . . . . . . . . . . . . . . . . . . 80
5.1.2. Representación . . . . . . . . . . . . . . . . . . . . . . 81
5.2. Implementación . . . . . . . . . . . . . . . . . . . . . . . . . . 82
5.3. Colas de prioridad . . . . . . . . . . . . . . . . . . . . . . . . 86
5.3.1. Cola de prioridad ascendente . . . . . . . . . . . . . . . 88
vi

8. 6.3.1. Implementacion de una pila utilizando herencia . . . . 110
6.3.2. Implementacion de una pila utilizando composición . . 115
ÍNDICE GENERAL
5.3.2. Cola de prioridad descendente . . . . . . . . . . . . . . 94
5.4. Consideraciones finales . . . . . . . . . . . . . . . . . . . . . . 95
5.5. Ejercicios . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 97
6. Listas enlazadas 103
6.1. Definición . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 103
103
6.1.1. Operaciones primitivas . . . . . . . . . . . . . . . . . . 104
6.1.2. Representación . . . . . . . . . . . . . . . . . . . . . . 105
6.2. Implementación . . . . . . . . . . . . . . . . . . . . . . . . . . 106
6.3. Herencia vs. composición . . . . . . . . . . . . . . . . . . . . . 110
6.4. Listas circulares . . . . . . . . . . . . . . . . . . . . . . . . . . 117
6.4.1. El problema de Josephus . . . . . . . . . . . . . . . . . 119
6.5. Listas doblemente enlazadas . . . . . . . . . . . . . . . . . . . 119
6.5.1. Definición, primitivas y representación . . . . . . . . . 120
6.6. Consideraciones finales . . . . . . . . . . . . . . . . . . . . . . 122
6.7. Ejercicios . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 123
7. Árboles binarios 129
7.1. Definición . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 129
7.1.1. Representación y conceptos . . . . . . . . . . . . . . . 129
7.1.2. Operaciones primitivas . . . . . . . . . . . . . . . . . . 131
7.2. Árbol binario de búsqueda (ABB) . . . . . . . . . . . . . . . . 134
7.2.1. Operaciones primitivas . . . . . . . . . . . . . . . . . . 135
7.2.2. Representación . . . . . . . . . . . . . . . . . . . . . . 136
7.2.3. Implementación . . . . . . . . . . . . . . . . . . . . . . 137
7.2.4. Eliminación . . . . . . . . . . . . . . . . . . . . . . . . 145
7.3. Árboles binarios balanceados (AVL) . . . . . . . . . . . . . . . 147
7.3.1. Definición y conceptos . . . . . . . . . . . . . . . . . . 147
7.3.2. Rotación simple . . . . . . . . . . . . . . . . . . . . . . 148
7.3.3. Rotación doble . . . . . . . . . . . . . . . . . . . . . . 150
7.4. Consideraciones finales . . . . . . . . . . . . . . . . . . . . . . 153
7.5. Ejercicios . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 154
A. Java 159
A.1. Orı́genes y caracterı́sticas . . . . . . . . . . . . . . . . . . . . . 160
A.2. Estructura general de una clase . . . . . . . . . . . . . . . . . 160
vii

9. ÍNDICE GENERAL
A.3. Bienvenid@ a Java . . . . . . . . . . . . . . . . . . . . . . . . 162
A.4. Compilación . . . . . . . . . . . . . . . . . . . . . . . . . . . . 164
A.5. Ejemplos selectos . . . . . . . . . . . . . . . . . . . . . . . . . 165
A.5.1. Lectura de datos . . . . . . . . . . . . . . . . . . . . . 165
A.5.2. Estructuras de control . . . . . . . . . . . . . . . . . . 167
A.5.3. Arreglos . . . . . . . . . . . . . . . . . . . . . . . . . . 170
A.5.4. Argumentos en la lı́nea de comandos . . . . . . . . . . 171
A.5.5. Excepciones . . . . . . . . . . . . . . . . . . . . . . . . 172
A.5.6. Genéricos . . . . . . . . . . . . . . . . . . . . . . . . . 174
A.6. Ejercicios . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 176
Bibliografı́a 179
Índice Analı́tico 181
Agradecimientos 187
Acerca del Autor 189
viii

10. Índice de figuras
1.1. Ilusión óptica del conejo-pato creada por Joseph Jastrow . . . 3
1.2. Jerarquı́a de clases . . . . . . . . . . . . . . . . . . . . . . . . 7
2.1. Salida del Ejemplo 2.2 . . . . . . . . . . . . . . . . . . . . . . 17
2.2. Salida del Ejemplo 2.4 . . . . . . . . . . . . . . . . . . . . . . 19
2.3. Salida del Ejemplo 2.6 . . . . . . . . . . . . . . . . . . . . . . 21
2.4. Salida del Ejemplo 2.8 . . . . . . . . . . . . . . . . . . . . . . 23
2.5. Salida del Ejemplo 2.10 . . . . . . . . . . . . . . . . . . . . . . 24
2.6. Diagrama de clases UML para la relación de herencia entre
Cientifico y Persona . . . . . . . . . . . . . . . . . . . . . . . 26
2.7. Salida del Ejemplo 2.13 . . . . . . . . . . . . . . . . . . . . . . 31
3.1. Salida de una ejecución del Ejemplo 3.2 al intentar crear un
número racional cuyo denominador sea cero . . . . . . . . . . 44
3.2. Salida de la ejecución del Ejemplo 3.2 . . . . . . . . . . . . . . 46
3.3. Representación de un objeto de la clase Nodo (Ejemplo 3.3) . 49
3.4. Secuencia de nodos generados por una clase autorreferida . . . 50
3.5. Representación de un objeto autorreferido . . . . . . . . . . . 54
4.1. Crecimiento y decrecimiento de una pila . . . . . . . . . . . . 56
4.2. Abstracción de una pila como una secuencia de nodos . . . . . 57
4.3. Inserción de elementos en la pila primitiva . . . . . . . . . . . 61
4.4. Eliminación de elementos de la pila primitiva . . . . . . . . . . 62
4.5. Diagrama de clases UML para la pila genérica . . . . . . . . . 73
5.1. Inserción y eliminación de elementos en una cola de espera . . 80
5.2. Abstracción de una cola de espera como una secuencia de nodos 81
5.3. Diagrama de clases UML para la cola de espera . . . . . . . . 81
5.4. Salida del Ejemplo 5.4 . . . . . . . . . . . . . . . . . . . . . . 87
ix

11. ÍNDICE DE FIGURAS
5.5. Diagrama de clases en UML para una cola de prioridad ascen-
dente con la redefinición del método elimina . . . . . . . . . . 88
5.6. Diagrama de clases en UML para una cola de prioridad ascen-
dente con la redefinición del método inserta . . . . . . . . . . 89
5.7. Salida del Ejemplo 5.6 . . . . . . . . . . . . . . . . . . . . . . 93
5.8. Diagrama de clases en UML para una cola de prioridad ascen-
dente con la redefinición del método elimina . . . . . . . . . . 94
5.9. Diagrama de clases en UML para una cola de prioridad ascen-
dente con la redefinición del método inserta . . . . . . . . . . 95
5.10. Abstracción y representación de Round robin . . . . . . . . . . 98
5.11. Abstracción de una estructura de datos compuesta . . . . . . . 102
6.1. Abstraccion de una lista enlazada como una secuencia de nodos105
6.2. Diagrama de clases UML para la lista enlazada . . . . . . . . 106
6.3. Salida del Ejemplo 5.4 . . . . . . . . . . . . . . . . . . . . . . 111
6.4. Diagrama de clases UML para la implementación de una pila
utilizando herencia y una lista lista enlazada . . . . . . . . . . 112
6.5. Salida del Ejemplo 6.4 . . . . . . . . . . . . . . . . . . . . . . 114
6.6. Diagrama de clases UML para la implementación de una pila
utilizando composición y una lista lista enlazada . . . . . . . . 115
6.7. Abstraccion de una lista enlazada circular como una secuencia
de nodos . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 118
6.8. Abstracción de una lista doblemente enlazada . . . . . . . . . 121
6.9. Diagrama de clases UML para una lista doblemente enlazada . 121
6.10. Representación de Round robin por niveles de prioridad . . . . 128
7.1. Abstraccion de un árbol binario como una estructura de nodos 130
7.2. Diagrama de clases UML para un árbol binario de búsqueda . 137
7.3. Una posible salida para el Ejemplo 7.3 y el Ejemplo 7.5 . . . . 142
7.4. Diagrama de clases UML para un árbol binario de búsqueda
con eliminación . . . . . . . . . . . . . . . . . . . . . . . . . . 147
7.5. Caso 1: Rotación derecha [Wirth] . . . . . . . . . . . . . . . . 149
7.6. Ejemplo de aplicación de la rotación sencilla . . . . . . . . . . 150
7.7. Caso 3: Rotación doble izquierda derecha (adaptada de [Wirth])151
7.8. Ejemplo de aplicación de la rotación doble . . . . . . . . . . . 152
7.9. Representación de un ABB . . . . . . . . . . . . . . . . . . . . 154
7.10. Eliminación en un árbol AVL (adaptada de [Wirth]) . . . . . . 158
x

12. ÍNDICE DE FIGURAS
A.1. Salida del Ejemplo A.2 . . . . . . . . . . . . . . . . . . . . . . 163
A.2. Salida del Ejemplo A.4 . . . . . . . . . . . . . . . . . . . . . . 163
A.3. Salida del Ejemplo A.6 . . . . . . . . . . . . . . . . . . . . . . 167
A.4. Salida del Ejemplo A.7 . . . . . . . . . . . . . . . . . . . . . . 169
A.5. Salida de los Ejemplos A.8, A.9 y A.10 . . . . . . . . . . . . . 170
A.6. Salida del Ejemplo A.11 . . . . . . . . . . . . . . . . . . . . . 171
A.7. Salida del Ejemplo A.12 sin argumentos . . . . . . . . . . . . 172
A.8. Salida del Ejemplo A.12 con argumentos . . . . . . . . . . . . 172
A.9. Relación UML de la jerarquı́a de la clases Exception en Java . 173
xi

14. Índice de ejemplos
2.1. Definición de la clase Parvulo1 . . . . . . . . . . . . . . . . . . 16
2.2. Clase de prueba para la clase Parvulo1 . . . . . . . . . . . . . 16
2.3. Definición de la clase Parvulo2 . . . . . . . . . . . . . . . . . . 18
2.4. Clase de prueba para la clase Parvulo2 . . . . . . . . . . . . . 18
2.5. Definición de la clase Parvulo3 . . . . . . . . . . . . . . . . . . 19
2.6. Clase de prueba para la clase Parvulo3 . . . . . . . . . . . . . 20
2.7. Definición de la clase Parvulo4 . . . . . . . . . . . . . . . . . . 22
2.8. Clase de prueba para la clase Parvulo4 . . . . . . . . . . . . . 23
2.9. Definición de la clase Parvulo5 . . . . . . . . . . . . . . . . . . 24
2.10. Clase de prueba para la clase Parvulo5 . . . . . . . . . . . . . 24
2.11. Definición de la clase Persona . . . . . . . . . . . . . . . . . . 28
2.12. Definición de la clase Cientifico . . . . . . . . . . . . . . . . . 30
2.13. Clase de prueba para la herencia . . . . . . . . . . . . . . . . 32
3.1. Clase implementa la abstracción de un número racional . . . . 44
3.2. Clase de prueba para la clase Racional . . . . . . . . . . . . . 47
3.3. Clase autorreferida . . . . . . . . . . . . . . . . . . . . . . . . 49
4.1. Definición de la clase NodoPrimitivo . . . . . . . . . . . . . . 57
4.2. Definición de la clase PilaPrimitiva . . . . . . . . . . . . . . . 58
4.3. Definición de la clase ExcepcionEDVacia que se utiliza para la
implementación de todas las estructuras de datos . . . . . . . 60
4.4. Clase de prueba para la clase PilaPrimitiva . . . . . . . . . . . 61
4.5. Definición de la clase para un nodo genérico (NodoG) . . . . . 63
4.6. Definición de la clase Pila que permite almacenar objetos genéri-
cos . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 64
4.7. Clase de prueba para la pila genérica . . . . . . . . . . . . . . 65
5.1. Nodo genérico utilizado en la cola de espera . . . . . . . . . . 82
5.2. Excepción utilizada en la cola de espera . . . . . . . . . . . . 83
xiii

15. ÍNDICE DE EJEMPLOS
5.3. Definición de la clase Cola que permite almacenar objetos
genéricos . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 84
5.4. Clase de prueba para la cola de espera . . . . . . . . . . . . . 86
5.5. Clase que define una cola de prioridad ascendente sobre escri-
biendo el método inserta . . . . . . . . . . . . . . . . . . . . . 90
5.6. Clase de prueba para la cola de prioridad ascendente . . . . . 92
5.7. Clase que implementa la interfaz Comparable . . . . . . . . . . 99
6.1. Definición de la clase Lista que permite almacenar objetos
genéricos . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 107
6.2. Clase de prueba para la clase Lista . . . . . . . . . . . . . . . 109
6.3. Definición de la clase PilaH que implementa una pila de obje-
tos genéricos utilizando herencia y una lista enlazada . . . . . 112
6.4. Clase de prueba para PilaH . . . . . . . . . . . . . . . . . . . 113
6.5. Definición de la clase PilaC que implementa una pila de obje-
tos genéricos utilizando composición y una lista enlazada . . . 116
6.6. Clase de prueba para PilaC . . . . . . . . . . . . . . . . . . . 117
7.1. Definición de la clase NodoABB que permite representar ob-
jetos (nodos) genéricos para un árbol binario de búsqueda . . 138
7.2. Definición de la clase ABBr que permite almacenar nodos (No-
doABB) en un árbol binario de búsqueda . . . . . . . . . . . . 139
7.3. Clase de prueba para el árbol binario de búsqueda (recursivo) 141
7.4. Definición de la clase ABB que permite almacenar nodos (No-
doABB) en un árbol binario de búsqueda . . . . . . . . . . . . 143
7.5. Clase de prueba para el árbol binario de búsqueda . . . . . . . 145
A.1. Estructura general de una clase en Java . . . . . . . . . . . . . 161
A.2. Primer programa en Java (versión 1.0) . . . . . . . . . . . . . 162
A.3. Primer programa en Java (versión 1.1) . . . . . . . . . . . . . 163
A.4. Primer programa en Java (versión 1.2) . . . . . . . . . . . . . 163
A.5. Primer programa en Java (versión 1.3) . . . . . . . . . . . . . 164
A.6. Lectura de datos desde la entrada estándar . . . . . . . . . . . 166
A.7. Uso de la estructura de selección if y de los operadores rela-
cionales . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 168
A.8. Estructura de repetición while . . . . . . . . . . . . . . . . . 169
A.9. Estructura de repetición do-while . . . . . . . . . . . . . . . 170
A.10.Estructura de repetición for . . . . . . . . . . . . . . . . . . . 170
A.11.Arreglo de enteros (int) . . . . . . . . . . . . . . . . . . . . . 171
A.12.Procesamiento de argumentos en la lı́nea de comandos . . . . 172
A.13.Definición de una excepción . . . . . . . . . . . . . . . . . . . 174
xiv

16. ÍNDICE DE EJEMPLOS
A.14.Uso de una colección ArrayList . . . . . . . . . . . . . . . . . 177
xv

18. Prefacio
Estimado lector, este libro tiene una orientación especı́fica. Está pensado
para un curso introductorio de programación orientada a objetos, en donde,
de manera preferente aunque de ninguna manera obligatoria, se haya tenido
un contacto previo con algún lenguaje de programación utilizando el enfo-
que estructurado; sin embargo, también es mi intención que el libro sea de
utilidad para aquellos lectores que se quieran iniciar en el mundo de la pro-
gramación y el paradigma orientado a objetos, sin ningún requisito previo de
programación.
El libro asume que el lector posee conocimientos básicos de algoritmos
y/o programación, ası́ como el funcionamiento de las estructuras de control
secuencial, de selección, y de repetición. Por otro lado, si bien es cierto que
para la comprensión del paradigma no es preciso dichos conocimientos (de
hecho podrı́an generar un vicio para un paradigma de programación orien-
tado a objetos más puro), sı́ lo son para la comprensión y el seguimiento
correspondiente de los programas de ejemplo.
Con todo, el libro proporciona un apéndice para apoyar al lector a través
de ejemplos selectos, tanto en la introducción del lenguaje de programación
utilizado, como en los conceptos fundamentales de la programación.
Al respecto, existe un debate acerca de si es mejor enseñar el paradig-
ma orientado a objetos sin antes tener un conocimiento de otro enfoque de
programación (como el estructurado por ejemplo), o si es mejor partir de la
programación estructurada para realizar una transición hacia la programa-
ción orientada a objetos. En mi opinión ambos enfoques tienen sus ventajas
y desventajas, y se podrı́a estar ante el sempiterno problema del huevo y la
gallina.
Java es un lenguaje de programación hı́brido, en el sentido de que no es
un lenguaje totalmente orientado a objetos como Smalltalk, y en ese sentido,
tiene estructuras de control y tipos de datos primitivos al estilo del lenguaje
xvii

19. PREFACIO
de programación C, el cual es el lenguaje por antonomasia para la progra-
macion estructurada y, dado que este libro utiliza a Java como lenguaje de
programación, aquellos lectores que conozcan el lenguaje C se sentirán fami-
liarizados rápidamente con Java, concentrándose entonces en la asimilación
del paradigma y en su aplicación.
Por otro lado, aquellos lectores que no conozcan el enfoque estructurado
estarı́an, al menos de primera instancia, sin la predisposición a cometer uno
de los vicios más comunes en la programación orientada a objetos, como lo es
el de utilizar Java por ejemplo, para escribir programas siguiendo un enfoque
estructurado. En éste sentido, resulta fundamental enfatizar desde ahora que
el uso de un lenguaje de programación orientado a objetos, no hace per se, ni
mucho menos garantiza, que los programas que se escriban en dicho lenguaje
sigan el modelo de programación orientado a objetos.
Como en muchas cosas, más que establecer qué es lo mejor y qué no
lo es, ya que se está ante una disyuntiva subjetiva, finalmente el beneficio
dependerá tanto de las intenciones del lector, como de su disposición hacia la
comprensión del paradigma orientado a objetos, ası́ como de que se entienda,
que la asimilación de un nuevo enfoque de programación no es excluyente de
otros, sino que la diversidad de enfoques de solución o formas de resolver un
problema, amplı́an el repertorio de conocimientos y capacidades intelectuales
en pro de ser progresiva y eventualmente, mejores programadores.
Para ilustrar y complementar de mejor manera tanto el diseño como los
conceptos relacionados con los objetos, el libro se apoya de diagramas de
clase UML para su correspondiente representación, por lo que serı́a también
de mucha utilidad tener bases de UML, sin embargo, tampoco son indispen-
sables.
La intención de este libro es también la de introducir al lector en algunas
de las estructuras de datos más convencionales, y al mismo tiempo, utilizarlas
para ilustrar los conceptos del paradigma orientado a objetos a través de su
implementación. En éste sentido, la estructura general del libro, es la que se
describe a continuación:
Capı́tulo 1 presenta los elementos fundamentales de la orientación a obje-
tos. La intención del capı́tulo es la de proporcionar al lector un pano-
rama general del paradigma orientado a objetos sin asociarlo necesa-
riamente con la programación, y mucho menos con algún lenguaje de
programación en particular.
xviii

20. Capı́tulo 2 describe las bases del paradigma orientado a objetos en el con-
texto de su aplicación a la programación, utilizando a Java como len-
guaje de programación.
La intención del capı́tulo es la de concretizar en un lenguaje de progra-
macion especı́fico, los conceptos más distintivos del paradigma orienta-
do a objetos, para que en los capı́tulos siguientes, se puedan aplicar al
desarrollo de las estructuras de datos, y mejorar ası́ tanto su compren-
sión, como la experiencia del lector de manera progresiva.
Capı́tulo 3 presenta un panorama general de las estructuras de datos, tipos
de datos y referencias en Java. Se aborda también un concepto central
tanto para el paradigma orientado a objetos, como para las estructuras
de datos: los tipos de datos abstractos (ADT). Ası́ mismo, se sientan
las bases para la implementación de estructuras de datos basadas en
clases de autorreferencia.
Capı́tulo 4 presenta la primera de las estructuras de datos estudiadas en
el libro. El capı́tulo comienza con la definición de las propiedades y
operaciones definidas para el ADT pila, para después presentar la im-
plementación de una pila utilizando un tipo de dato primitivo. Poste-
riormente, tomando como base dicha implementación, se generaliza el
concepto para mostrar la implementación de una pila cuyos elementos
son objetos genéricos. Finalmente, se refuerza la definición del ADT, y
se muestra la relación que existe entre la implementación y el diseño
con el correspondiente diagrama de clases en UML.
Capı́tulo 5 introduce al lector en el estudio de las estructuras de datos de-
nominadas colas de espera. Se realiza una presentación de la cola de
espera ası́ como de su correspondiente implementación, para posterior-
mente analizar una variante de dicha estructura de datos: las colas de
prioridad. Ası́ mismo, el capı́tulo también presenta los elementos princi-
pales para la implementación de objetos con caracterı́sticas de relación
de orden a través de la interfaz Comparable del API de Java. Dicha
caracterı́stica resultará fundamental para los capı́tulos posteriores.
Capı́tulo 6 presenta al lector la última de las estructuras de datos linea-
les estudiadas en el libro: las listas enlazadas. Ası́ mismo, toda vez
que se asume completado el estudio de las pilas, el capı́tulo muestra
la posibilidad de la implementación de dicha estructura de datos por
xix

21. PREFACIO
medio de una lista enlazada. Adicionalmente, se comentan las ventajas
y desventajas de los enfoques de implementación utilizados.
Capı́tulo 7 introduce al lector tanto a los conceptos de árboles binarios,
como al conocimiento de algunas de las estructuras de datos de árboles
mas comunes: árboles binarios, árboles binarios de búsqueda (ABB), y
árboles AVL.
Los árboles binarios son estructuras de datos no lineales, y sus aplica-
ciones y usos son tan diversos, que están únicamente limitados por la
imaginación de quien los utiliza. El capı́tulo inicia presentando los con-
ceptos relacionados con los árboles binarios en general, y con los ABB
y AVL en particular. Presenta además dos tipos de implementación
para un ABB: con recursividad y con ciclos, y se describen también los
diferentes recorridos que es posible realizar con árboles binarios.
Apéndice A presenta un compendio de referencia a la mano de Java para
el lector familiarizado con algún lenguaje de programación. Al mismo
tiempo, es un marco de referencia respecto a caracterı́sticas que no se
tienen en un enfoque estructurado, como lo son las excepciones y los
genéricos por ejemplo. El apéndice presenta además una selección de
ejemplos de transición respecto a la forma de hacer las cosas en Java,
sin entrar en detalles especı́ficos respecto a la definición y descripción
de las estructuras de control, representación y notación de arreglos, etc.
Insisto en que este libro tiene una naturaleza introductoria, pero no por
ello informal. Confı́o plenamente en que puede servir como inicio de un largo
camino en la asimilación progresiva de los conceptos asociados con el para-
digma orientado a objetos. Espero sinceramente haber podido alcanzar la
meta de transmitir los conceptos fundamentales de la orientación a objetos,
ası́ como su aplicación en las estructuras de datos, utilizando al lenguaje de
programación Java como medio.
Ricardo Ruiz Rodrı́guez
xx

22. I consider to paradigms as universally recognized scientific
achievements that, for a time, provide model problems and
solutions for a community of researchers.
Thomas Samuel Kuhn
Programming is one of the most difficult branches of applied
mathematics; the poorer mathematicians had better remain pure
mathematicians.
Edsger Wybe Dijkstra
xxi

24. Capı́tulo 1
Orientación a Objetos
Technology is anything that wasn’t around when you were born.
Alan Curtis Kay
Hong Kong press conference
1.1. Orı́genes
Las caracterı́sticas principales de lo que actualmente se denomina Pro-
gramación Orientada a Objetos (POO) surgen en 1960, y aunque algunos
autores difieren en sus orı́genes, los conceptos de la POO tienen su inicio en
Simula 67, un lenguaje diseñado en el centro de cómputo noruego en Oslo1
.
Posteriormente, en Agosto de 1981, se publica en la revista Byte la des-
cripción del lenguaje de programación Smalltalk2
, el cual refinó algunos de
los conceptos originados con el lenguaje Simula.
Lo anterior dio pie a que en la década de 1980, los lenguajes de progra-
mación Orientados a Objetos (OO) tuvieran un rápido auge y expansión,
por lo que la POO se fue convirtiendo en el estilo de programación dominan-
te a mediados de los años ochenta del siglo XX, continuando vigente hasta
nuestros dı́as.
La POO es una de las propuestas de solución para ayudar a resolver
la denominada, aunque no generalmente aceptada, “crisis del software”. En
este sentido, es importante decir que, si bien las técnicas OO facilitan la
1
Lenguaje para simulaciones creado por Ole-Johan Dahl y Kristen Nygaard.
2
Desarrollado en Xerox PARC (Palo Alto-California Research Center).
1

25. 2 CAPÍTULO 1. ORIENTACIÓN A OBJETOS
creación de complejos sistemas de software por medio de mejores mecanismos
de abstracción, no son la panacea universal de solución.
Programar una computadora sigue siendo una de las tareas más difı́ci-
les jamás realizadas por un ser humano. Volverse experto en programación
requiere, no sólo de saber manejar herramientas y conocer técnicas de pro-
gramación, sino que es preciso contar también con:
Talento.
Creatividad.
Inteligencia.
Lógica.
Habilidad para construir y utilizar abstracciones.
Experiencia.
Por lo anterior, hacer un uso efectivo de los principios OO requiere de
una visión del mundo desde una perspectiva distinta, sobre todo si se parte
de la base de resolución de problemas a través de un enfoque estructurado.
Es importante señalar y tener presente desde este momento, que el uso de
un lenguaje de POO no hace, por sı́ mismo, que se programe OO, ya que se
podrı́a tener en el mejor de los casos, un programa o sistema implementado
con un enfoque estructurado, pero programado en un lenguaje orientado a
objetos.
La POO requiere de la comprensión del paradigma orientado a objetos.
La sección 1.2 discute el concepto de paradigma que se utilizará a lo largo
del texto.
1.2. Paradigma
El concepto de paradigma resulta fundamental en la comprensión del
paradigma orientado a objetos.
Antes de proporcionar la definición que se adoptará, describiré algunas
definiciones de paradigma que encontré:
paradigma m. Ejemplo o ejemplar: esa chica es el paradigma de la pacien-
cia.

26. 1.2. PARADIGMA 3
Figura 1.1: Ilusión óptica del conejo-pato creada por Joseph Jastrow
paradigma ling. Cada uno de los esquemas formales a los que se ajustan las
palabras, según sus respectivas flexiones: paradigma de la conjugación
verbal.
paradigma ling. Conjunto de elementos de una misma clase gramatical que
pueden aparecer en un mismo contexto: paradigma de las preposiciones.
paradigma ejemplo o modelo. En todo el ámbito cientı́fico, religioso u otro
contexto epistemológico, el término paradigma puede indicar el concep-
to de esquema formal de organización, y ser utilizado como sinónimo
de marco teórico o conjunto de teorı́as.
Pero entonces, ¿qué entender por paradigma de programación?
La palabra paradigma irrumpió en el vocabulario moderno a través del
influyente libro “The Structure of Scientific Revolutions”del historiador de
la ciencia Thomas Samuel Kuhn[Kuhn].
Thomas Kuhn utilizó el término en la forma de la última definición: un
paradigma es un modelo para describir un conjunto de teorı́as, estándares y
métodos que en conjunto representan una forma de organizar el conocimiento,
esto es, una forma de ver el mundo.
En base a lo anterior se entederá como paradigma de programación
al modelo de programación utilizado, el cual está descrito y definido por un
conjunto de teorı́as, estándares y métodos que en conjunto, representan una
propuesta de solución por software hacia una problemática determinada.

27. 4 CAPÍTULO 1. ORIENTACIÓN A OBJETOS
Kuhn utilizó la ilusión óptica de la Figura 1.1 para ilustrar el concepto
de paradigma. En dicha figura puede verse un conejo o un pato, dependiendo
de la perspectiva que se utilice.
El paradigma orientado a objetos cambió la perspectiva respecto del en-
foque estructurado, el cual era el paradigma dominante hasta entonces.
1.2.1. Una perspectiva diferente
El concepto sobre el que subyace la esencia de la orientación a objetos
es la abstracción. Por lo que, al pensar en este paradigma, deberá tener en
mente una perspectiva basada en los siguientes conceptos:
1. Entidades: agentes u objetos en interacción, donde cada objeto tiene
un rol.
2. Responsabilidades: cada objeto proporciona un conjunto de servicios
o lleva a cabo acciones que son utilizadas por otras entidades u objetos.
Las responsabilidades determinan el comportamiento del objeto.
3. Mensajes: en la POO la acción es iniciada por la transmisión de un
mensaje a un objeto responsable de dicha acción. En respuesta al men-
saje, el objeto receptor llevará a cabo un método para satisfacer la
solicitud que le fue realizada por dicho mensaje.
Los tres elementos anteriormente mencionados, constituyen los funda-
mentos primordiales de la orientación a objetos. A lo largo del texto se desa-
rrollarán de manera progresiva, y se ejemplificarán con programas.
Mensajes, procedimientos/funciones y métodos
Los mensajes son solicitudes especı́ficas de alguno de los servicios o res-
ponsabilidades asignadas a un objeto. Los mensajes tienen un receptor es-
pecı́fico, por lo que son enviados a un objeto en particular con una posible
lista de argumentos determinada.
Los mensajes son llevados a cabo por métodos, los cuales son algoritmos
asociado a un objeto (o a una clase de objetos), cuya ejecución se desencadena
tras la recepción de un mensaje. En este sentido, tanto los métodos como los
procedimientos o funciones son un conjunto de pasos bien definidos que llevan
a cabo una acción; sin embargo, los mensajes y los procedimientos o funciones
se distinguen esencialmente por dos aspectos:

28. 1.2. PARADIGMA 5
1. En un mensaje, hay un receptor designado para dicho mensaje.
2. La interpretación o método utilizado para responder al mensaje es de-
terminado por el receptor, y puede variar en función del receptor.
1.2.2. Objetos
Los objetos son esencialmente abstracciones. Son entidades que tienen un
determinado estado, un comportamiento (determinado por sus responsabili-
dades), y una identidad.
El estado está representado por los datos o los valores que contienen los
atributos del objeto, los cuales son a su vez, otros objetos o variables
que representan las caracterı́sticas inherentes del objeto.
El comportamiento está determinado por las responsabilidades o servicios
del objeto, los cuales son definidos por los métodos, mismos que se
solicitan a través de mensajes a los que sabe responder dicho objeto.
La identidad es la propiedad que tiene un objeto que lo distingue de los
demás. La identidad está representada por un identificador.
Un objeto es una entidad que contiene en sı́ mismo, toda la información
necesaria, misma que permite definirlo, identificarlo, y accederlo3
frente a
otros objetos pertenecientes a otras clases, e incluso frente a objetos de su
misma clase.
Los objetos se valen de mecanismos de interacción llamados métodos,
que favorecen la comunicación entre ellos. Dicha comunicación favorece a su
vez el cambio de estado en los propios objetos. Esta caracterı́stica define a
los objetos como unidades indivisibles, en las que no se separa el estado del
comportamiento.
Orientación a objetos vs. enfoque estructurado
La orientación a objetos difiere del enfoque estructurado básicamente, en
que en la programación estructurada los datos y los procedimientos están
3
La forma de acceder a un objeto es a través de su interfaz. La interfaz de un objeto
es el conjunto de servicios públicos que ofrece el objeto, los cuales se solicitan a través de
mensajes o solicitudes realizadas a dicho objeto.

29. 6 CAPÍTULO 1. ORIENTACIÓN A OBJETOS
separados y sin relación, ya que lo único que se busca en ésta última, es el
procesamiento de los datos de entrada para obtener los datos de salida.
La programación estructurada utiliza en primera instancia, un enfoque
basado en procedimientos o funciones, y en segunda instancia, las estructuras
de datos que dichos procedimientos o funciones manejan, cumpliendo ası́ la
Ecuación 1.1 planteada por Niklaus Wirth.
Algoritmos + Estructuras de Datos = Programas (1.1)
Por otro lado, un programa en un enfoque OO solicita estructuras de
datos (las cuales son otros objetos) para llevar a cabo un servicio.
La perspectiva OO también define programas compuestos por algoritmos
y estructuras de datos esencialmente (como los de la Ecuación 1.1), sin em-
bargo lo hace desde un enfoque diferente. En la orientación a objetos la des-
cripción del objeto se da en términos de responsabilidades y caracterı́sticas, y
al analizar un problema en dichos términos, se eleva el nivel de abstracción.
Lo anterior permite una mayor independencia entre los objetos, lo cual
es un factor crı́tico en la solución de problemas complejos. Cabe mencionar
por último, que al conjunto completo de responsabilidades asociadas con un
objeto es comúnmente referido como protocolo.
1.2.3. Objetos y clases
Todos los objetos son instancias de una clase (categorı́a). Esta relación
de un objeto con una clase, hace que los objetos tengan las siguientes carac-
terı́sticas:
El método invocado por un objeto en respuesta a un mensaje, es de-
terminado por la clase del objeto receptor.
Todos los objetos de una clase determinada, utilizan el mismo método
en respuesta a mensajes similares.
Las clases pueden ser organizadas en una estructura jerárquica de he-
rencia como la que se muestra en la Figura 1.2.
Una clase hija o subclase heredará todas las caracterı́sticas de la clase
de la que deriva (clase padre).

30. 1.2. PARADIGMA 7
Figura 1.2: Jerarquı́a de clases
Una clase abstracta es una clase de la que no se derivan instancias
directamente, sino que es utilizada únicamente para crear subclases.
La búsqueda del método a invocar en respuesta a un mensaje deter-
minado, inicia en la clase del receptor. Si no se encuentra el método
apropiado, la búsqueda se realiza en la clase padre, y ası́ sucesivamente
hasta encontrar el método correspondiente.
Si se encuentran métodos con el mismo nombre dentro de la jerarquı́a
de clases, se dice que el método procesado sobre escribe (override) el
comportamiento heredado.
La Figura 1.2 presenta una posible jerarquı́a de clases para un Ser Vivo.
Mas que una clasificación o taxonomı́a completa, la figura muestra el concepto
de herencia a través de un árbol, el cual exhibe, que los elementos que se
derivan, comparten caracterı́sticas (atributos) y comportamientos (métodos)
semejantes.
Ası́ por ejemplo, es posible decir que Flipper es una instancia particular de
todos los posibles delfines que podrı́an existir. A su vez, un Delfı́n comparte

31. 8 CAPÍTULO 1. ORIENTACIÓN A OBJETOS
caracterı́sticas comunes con una Ballena en cuanto a que ambos son Cetáceos,
pero difieren en otras4
.
Un Delfı́n es un Cetáceo, y un Cetáceo es un Mamı́fero. En muchas oca-
siones a éste tipo de relaciones se le denomina “es un”(is a), y es una carac-
terı́stica útil para identificar herencia, pero no es la única.
Existe otro tipo de relación y se denomina “tiene” (has-a). Estas relacio-
nes son las dos formas más importantes de abstracción en la orientación a
objetos:
1. La idea de división en partes (has-a): un automóvil tiene un motor,
tiene una transmisión, tiene un sistema eléctrico, etc.
2. La idea de división en especializaciones (is-a): un automóvil es un
medio de transporte, es un objeto de cuatro ruedas, es un objeto que
se dirige con un volante, etc.
Finalmente, la Figura 1.2 muestra que Flipper es un Delfı́n, que un Delfı́n
es un Cetáceo, y que éste a su vez es un Mamı́fero; que un Mamı́fero per-
tenece al Reino Animal, y que el Reino Animal es parte de los seres vivos
representados por la super clase o clase base Ser Vivo.
1.3. Orientación a objetos y modularidad
La modularidad no está exclusivamente relacionada con los procedimien-
tos o funciones de la programación estructurada, sino con el grado en el que
los componentes de un sistema pueden ser separados y reutilizados.
En base a lo anterior, tanto los métodos como los objetos son en sı́ mismos
módulos de una aplicación determinada, y en consecuencia, las clases de las
que se derivan constituyen los módulos del sistema, por lo que de aquı́ en
adelante se hará referencia a la modularidad de manera indistinta tanto para
clases, como para los métodos de las clases.
La modularidad ayuda también a hacer el código más comprensible, y ésto
a su vez hace que en consecuencia el código sea más fácil de mantener. Sin
embargo, sin las debidas consideraciones, la modularidad tiene también sus
consecuencias negativas, las cuales están en función directa de dos conceptos
4
Si un delfı́n y una ballena coincidieran en todo (caracterı́sticas y comportamiento)
serı́an de la misma clase.

32. 1.4. CARACTERÍSTICAS FUNDAMENTALES DE LA POO 9
fundamentales en el desarrollo de software en general, y en el paradigma
orientado a objetos en particular:
1. Cohesión.
2. Acoplamiento.
1.3.1. Cohesión y Acoplamiento
La cohesión está relacionada con la integridad interna de un módulo. Es
el grado o nivel de relación o integridad entre los elementos que componen
un módulo.
El nivel de cohesión determina, qué tan fuerte están relacionados cada
unos de los elementos de funcionalidad expresados en el código fuente de un
módulo.
Por otro lado, el acoplamiento describe qué tan fuerte un módulo está re-
lacionado con otros, es decir, es el grado en que un módulo depende de cada
uno de los otros módulos que componen un sistema.
El acoplamiento también puede ser referido o entendido como dependen-
cia, lo cual ayuda a recordar que lo que se desea es mantener un bajo nivel
de dependencia entre los módulos, es decir un bajo acoplamiento.
En general, se desea que los módulos de un programa o sistema tengan,
un alto nivel de cohesión y un bajo nivel de acoplamiento, y el paradigma
orientado a objetos persigue y enfatiza dichos objetivos.
1.4. Caracterı́sticas fundamentales de la POO
Por último, pero no por ello menos importante, es importante mencionar
que Alan Curtis Kay, quien es considerado por muchos como el padre de la
POO, definió un conjunto de caracterı́sticas fundamentales para el paradig-
ma.
En base a lo propuesto por Kay, en la Programación Orientada a Objetos:
1. Todo es un objeto.
2. El procesamiento es llevado a cabo por objetos:

33. 10 CAPÍTULO 1. ORIENTACIÓN A OBJETOS
Los objetos se comunican unos con otros solicitando que se lleven
a cabo determinadas acciones.
Los objetos se comunican enviando y recibiendo mensajes.
Un mensaje es la solicitud de una acción, la cual incluye los argu-
mentos que son necesarios para completar la tarea.
3. Cada objeto tiene su propia memoria, misma que está compuesta de
otros objetos.
4. Cada objeto es una instancia de una clase. Una clase representa un
grupo de objetos similares.
5. La clase es el repositorio del comportamiento asociado con un objeto.
Todos los objetos que son instancias de la misma clase, llevan a
cabo las mismas acciones.
6. Las clases están organizadas en una estructura jerárquica de árbol de-
nominada jerarquı́a de herencia.
La memoria y el comportamiento asociados con las instancias de
una clase, están automáticamente disponibles para cualquier clase
asociada con la descendencia dentro de la estructura jerárquica de
árbol.
Complementando la visión de Alan Kay, se presenta a continuación un
compendio de conceptos que definen también y refuerzan, las caracterı́sticas
principales de la POO:
La abstracción denota las caracterı́sticas esenciales de un objeto.
El proceso de abstracción permite seleccionar las caracterı́sticas rele-
vantes dentro de un conjunto, e identificar comportamientos comunes
para definir nuevos tipos de entidades.
La abstracción es la consideración aislada de las cualidades esenciales
de un objeto en su pura esencia o noción.
La modularidad es la propiedad que permite subdividir una aplicación en
partes más pequeñas (llamadas módulos), cada una de las cuales debe

34. 1.4. CARACTERÍSTICAS FUNDAMENTALES DE LA POO 11
ser tan independiente como sea posible de la aplicación en sı́, y de las
partes restantes.
La modularidad es el grado en el que los componentes de un sistema
pueden ser separados y reutilizados.
El encapsulamiento tiene que ver con reunir todos los elementos que pue-
den considerarse pertenecientes a una misma entidad, al mismo nivel
de abstracción. Esto permite aumentar la cohesión de los módulos o
componentes del sistema.
El principio de ocultación de información (information hiding) se re-
fiere a que cada objeto está aislado del exterior, es un módulo indepen-
diente, y cada tipo de objeto presenta una interfaz a otros objetos, la
cual especifica cómo es que pueden interactuar con él.
El aislamiento protege a las propiedades de un objeto contra su mo-
dificación por quien no tenga derecho a acceder a ellas; solamente los
propios métodos internos del objeto pueden acceder a su estado. Ésto
asegura que otros objetos no puedan cambiar el estado interno de un
objeto de manera accidental o intencionada, eliminando efectos secun-
darios e interacciones inesperadas.
El polimorfismo está relacionado con el aspecto de que comportamientos
diferentes asociados a objetos distintos, pueden compartir el mismo
nombre.
El polimorfismo es la capacidad que tienen los objetos de naturaleza
heterogénea, de responder de manera diferente a un mismo mensaje, en
función de las caracterı́sticas y responsabilidades del objeto que recibe
dicho mensaje.
La herencia organiza y facilita el polimorfismo y el encapsulamiento, per-
mitiendo a los objetos ser definidos y creados como tipos especializados
de objetos preexistentes.
Las clases no están aisladas, sino que se relacionan entre sı́ formando
una jerarquı́a de clasificación.
Los objetos heredan las propiedades y el comportamiento de todas las
clases a las que pertenecen. Ası́, los objetos pueden compartir y exten-
der su comportamiento sin tener que volver a implementarlo.

35. 12 CAPÍTULO 1. ORIENTACIÓN A OBJETOS
Cuando un objeto hereda de más de una clase se dice que hay herencia
múltiple.
Es importante tener todos estos conceptos presentes, estudiarlos, anali-
zarlos y comprenderlos, la memorización no es recomendable, ya que es bien
sabido que el memorizar conceptos no implica su comprensión, pero si un
concepto es comprendido, es posible explicarlo y deducir en consecuencia su
definición.
Mi deseo es que el lector reflexione sobre este aspecto y que, con un
poco de paciencia, sume a su repertorio de conocimientos el conjunto de
conceptos descritos hasta aquı́, los cuales se pondrán en práctica eventual y
progresivamente, en los capı́tulos siguientes.
1.5. Consideraciones finales
Este capı́tulo discutió los elementos fundamentales de la orientación a
objetos. La intención del capı́tulo es la de proporcionar al lector un panorama
general del paradigma orientado a objetos, sin asociarlo necesariamente con
la programación, y mucho menos con algún lenguaje de programación en
particular.
Un lenguaje de programación es sólo un medio para el paradigma, no el
paradigma en sı́. Por otro lado, el ejercicio de la programación es la forma
de aplicar los conceptos asociados al paradigma.
Los capı́tulos siguientes irán detallando al lector los conceptos presentados
hasta ahora, pero desde la perspectiva de la programación y su aplicación
en un lenguaje de programación. Sin embargo, es importante aclarar que
el objetivo del libro no es enseñar un lenguaje de programación, sino el de
utilizar al lenguaje como un medio para hacer tangibles los conceptos de
orientación a objetos.
El Apéndice A introduce algunos aspectos del lenguaje de programación
Java que podrı́an ser de utilidad para el lector, pero de ninguna manera
pretende cubrir los elementos completos de dicho lenguaje, sino solamente
presentar un panorama general.

36. 1.6. EJERCICIOS 13
1.6. Ejercicios
1. Investigue más acerca de la historia y desarrollo de la programación
orientada a objetos.
2. Xerox es actualmente una compañı́a que desarrolla equipo de foto copia-
do e impresión entre otras cosas. Investigue cuál era el sistema operativo
que utilizaban, que por cierto, ya incluı́a una GUI (Interfaz Gráfica de
Usuario), pionera de las GUI que actualmente se utilizan.
3. Investigue la historia y la ideologı́a del lenguaje de programación Small-
talk. Aproveche para conocer el nombre de su(s) creador(es).
4. Investigue la historia y la ideologı́a del lenguaje de programación Eiffel.
Aproveche para conocer el nombre de su(s) creador(es).
5. Investigue la historia del lenguaje de programación C++. Aproveche
para conocer el nombre de su(s) creador(es).
6. Investigue el papel del Dr. Alan Curtis Kay en la concepción y desa-
rrollo de la programación orientada a objetos.
7. Investigue qué otros paradigmas de programación existen.
8. Investigue qué lenguajes de programación actuales soportan el paradig-
ma orientado a objetos, cuáles lo soportan de manera nativa y cuáles
como una extensión.

37. 14 CAPÍTULO 1. ORIENTACIÓN A OBJETOS

38. Capı́tulo 2
Programación Orientada a
Objetos
Object-oriented programming is an exceptionally bad idea which
could only have originated in California.
Edsger Wybe Dijkstra (attributed to)
I don’t know how many of you have ever met Dijkstra, but you
probably know that arrogance in computer science is measured in
nano-Dijkstras.
Alan Curtis Kay
Este capı́tulo presenta las bases del paradigma orientado a objetos en
el contexto de su aplicación a la programación utilizando un lenguaje de
programación.
La intención principal del capı́tulo, es concretizar en un lenguaje de pro-
gramación los conceptos más distintivos del paradigma orientado a objetos,
para que en los capı́tulos subsecuentes, se puedan aplicar al desarrollo de las
estructuras de datos, y mejorar ası́ tanto la comprensión de los conceptos,
como la experiencia del lector.
Antes de continuar con este capı́tulo, no estarı́a de más que el lector
revisara el Apéndice A, a excepción de que se esté ampliamente familiarizado
con el lenguaje de programación Java.
15

39. 16 CAPÍTULO 2. PROGRAMACIÓN ORIENTADA A OBJETOS
2.1. Mensajes y métodos
Una de las principales inquietudes que expresan los estudiantes acerca
del paradigma orientado a objetos, está relacionada con los mensajes y los
métodos. En este sentido, se iniciará con un ejemplo sumamente sencillo, el
cual irá evolucionando progresivamente con la finalidad de ilustrar dichos
conceptos.
2.1.1. Métodos sin argumentos
El Ejemplo 2.1 muestra la definición de la clase Parvulo1, la cual no
contiene atributos, pero sı́ un método cuyo identificador o nombre es mensaje.
1 /∗ Ejemplo de envio de mensaje e invocacion de metodos ( Version 1.0) .
2 @autor Ricardo Ruiz Rodriguez
3 ∗/
4 public class Parvulo1 {
5 public void mensaje ( ) {
6 System . out . p r i n t l n ( ”Dentro del metodo mensaje ( ) ” ) ;
7 }
8 }
Ejemplo 2.1: Definición de la clase Parvulo1
El método mensaje tiene como única responsabilidad la impresión en la
salida estándar de una cadena1
.
En base a lo anterior, la clase Parvulo1 es una plantilla capaz de generar
objetos con una única responsabilidad o servicio, y no puede ser instanciada
ni ejecutada por sı́ misma. Para poder instanciar objetos de la clase Parvulo1
y poder visualizar su funcionamiento, se requiere de una clase de prueba
que permita generar una instancia de ella.
1 /∗ Clase de prueba para Parvulo1 . Se crea e l o b j e t o ” parvulo ” instanciado
2 de l a c l a s e Parvulo1 y se l e envia e l mensaje ”mensaje” .
3 @autor Ricardo Ruiz Rodriguez
4 ∗/
5 public class PruebaParvulo1{
6 public static void main ( String [ ] args ) {
7 Parvulo1 parvulo = new Parvulo1 () ;
8
9 parvulo . mensaje () ;
10 }
11 }
Ejemplo 2.2: Clase de prueba para la clase Parvulo1
1
Los detalles generales del funcionamiento de println son presentados en la Sección A.3.

40. 2.1. MENSAJES Y MÉTODOS 17
Figura 2.1: Salida del Ejemplo 2.2
La clase de prueba para el Ejemplo 2.1 es la clase PruebaParvulo1 que se
presenta en el Ejemplo 2.2.
La clase PruebaParvulo1 tiene la estructura de la mayorı́a de las clases
de prueba que se utilizarán en el texto, y está basada en la definición del
método main.
En la lı́nea 7 se define el objeto parvulo cuya clase (tipo) es Parvulo1;
ası́ mismo, observe que se genera una instancia por medio de la cláusula new,
el cual, entre otras cosas, construye el objeto. Si la clase Parvulo1 tuviera
un constructor explı́cito, serı́a precisamente aquı́ en donde se invocarı́a. Más
adelante en esta misma sección, se profundizará un poco más al respecto.
Una vez que el objeto existe (ha sido instanciado), es posible interactuar
con él por medio de mensajes para solicitarle acciones que correspondan con
las responsabilidades o servicios definidos para dicho objeto que, para el caso
del objeto parvulo, es sólo una.
La solicitud del único servicio que puede proporcionar el objeto parvulo se
realiza a través del mensaje mensaje, el cual es enviado (invocado) al objeto
en la lı́nea 9:
parvulo.mensaje();
La expresión anterior se interpreta como: “se envı́a el mensaje mensaje al
objeto parvulo”. El envı́o de mensajes no es otra cosa más que la invocación
explı́cita de un método a través de su identificador, es utilizar el método
correspondiente para realizar una acción, misma que está relacionada con el
comportamiento o las responsabilidades del objeto en cuestión.
La salida del Ejemplo 2.2 se muestra en la Figura 2.1. Asegúrese de com-
prender lo hasta aquı́ descrito antes de continuar.
2.1.2. Métodos con argumentos
En esta sección se presenta una versión ligeramente distinta del Ejemplo
2.1, en el cual se presentó el envı́o de mensajes sin argumentos. Tómese el
tiempo necesario para comparar el Ejemplo 2.3 de esta sección con el Ejemplo
2.1, y compruebe que son esencialmente iguales.
El argumento nombre en el método mensaje constituye la diferencia de los

41. 18 CAPÍTULO 2. PROGRAMACIÓN ORIENTADA A OBJETOS
ejemplos anteriormente mencionados. En el Ejemplo 2.3 el método mensaje
(lı́nea 5) define ahora la capacidad de recibir el argumento nombre, el cual
se define como un objeto de la clase String. El método mensaje imprime en
la salida estándar un cadena conformada por un texto predefinido (lı́nea 6)
y la cadena referida por nombre.
1 /∗ Ejemplo de envio de mensaje e invocacion de metodos ( Version 1.1) .
2 @autor Ricardo Ruiz Rodriguez
3 ∗/
4 public class Parvulo2 {
5 public void mensaje ( String nombre ) {
6 System . out . p r i n t l n ( ”Mi nombre es ” + nombre ) ;
7 }
8 }
Ejemplo 2.3: Definición de la clase Parvulo2
Por otro lado, el Ejemplo 2.4 muestra la clase de prueba para el Ejemplo
2.3, la cual es también similar a la del Ejemplo 2.2 excepto en la forma en
que se envı́a el mensaje al objeto parvulo (lı́nea 10 del Ejemplo 2.4). Observe
que el mensaje enviado tiene ahora una cadena como argumento, la cual es
referida por el objeto nombre del método mensaje (lı́nea 5 del Ejemplo 2.3)
en el momento en que se le envı́a el mensaje mensaje al objeto parvulo.
1 /∗ Clase de prueba para Parvulo2 . Se crea e l o b j e t o ” parvulo ”
2 instanciado de l a c l a s e Parvulo2 y se l e envia e l mensaje
3 ”mensaje” con un argumento .
4 @autor Ricardo Ruiz Rodriguez
5 ∗/
6 public class PruebaParvulo2{
7 public static void main ( String [ ] args ) {
8 Parvulo2 parvulo = new Parvulo2 () ;
9
10 parvulo . mensaje ( ” Ricardo ” ) ;
11 }
12 }
Ejemplo 2.4: Clase de prueba para la clase Parvulo2
Asegúrese de realizar una labor analı́tica al comparar lı́nea a lı́nea, tanto
las clases Parvulo1 y Parvulo2, como las clases PruebaParvulo1 y Prueba-
Parvulo2, ası́ como de comprender sus diferencias en base a lo que se ha
descrito hasta ahora.
La salida del Ejemplo 2.4 se muestra en la Figura 2.2.

42. 2.1. MENSAJES Y MÉTODOS 19
Figura 2.2: Salida del Ejemplo 2.4
2.1.3. Métodos y atributos
Por el principio de ocultación de información, es conveniente que única-
mente se tenga acceso a los atributos de una clase a través de su interfaz. La
interfaz de un objeto está representada por sus métodos públicos (public).
1 /∗ Ejemplo de envio de mensaje e invocacion de metodos ( Version 1.2) .
2 Se introducen l o s metodos s e t y get para a t r i b u t o s de c l a s e .
3 @autor Ricardo Ruiz Rodriguez
4 ∗/
5 public class Parvulo3 {
6 private String nombre ;
7
8 public void estableceNombre ( String n) {
9 nombre = n ;
10 }
11
12 public String obtenNombre () {
13 return nombre ;
14 }
15
16 public void mensaje ( ) {
17 System . out . p r i n t l n ( ”Mi nombre es ” + obtenNombre () ) ;
18 }
19 }
Ejemplo 2.5: Definición de la clase Parvulo3
El Ejemplo 2.5 hace uso de dicho principio al definir, con un acceso restrin-
gido o privado (private), el atributo nombre (lı́nea 6) para la clase Parvulo3.
Observe que dicha clase define también tres métodos públicos, los cuales es-
tablecen la interfaz de los objetos que sean instanciados:
1. estableceNombre: este método es utilizado comúnmente para ajus-
tar o establecer el valor de un atributo, y en principio, deberı́a ha-
ber un método de este tipo por cada atributo que contenga la clase y
que se requiera manipular desde el exterior. Este tipo de métodos son
comúnmente referidos como métodos de tipo set.
2. obtenNombre: este método es utilizado comúnmente para recuperar
u obtener el valor de un atributo, y al igual que antes, deberı́a ha-
ber un método de este tipo por cada atributo que contenga la clase y

43. 20 CAPÍTULO 2. PROGRAMACIÓN ORIENTADA A OBJETOS
que se requiera visualizar desde el exterior. Este tipo de métodos son
comúnmente referidos como métodos de tipo get.
3. mensaje: este tipo de métodos ha sido descrito con anterioridad. Note
que el método está definido como el del Ejemplo 2.1 (sin argumentos),
pero funciona como el del Ejemplo 2.3. Asegúrese de comprender ésto.
Observe que el método mensaje (lı́neas 16-18) se vale del método obten-
Nombre (lı́nea 17) para acceder al atributo nombre, pero no necesariamente
tiene que ser ası́, ya que un método puede acceder directamente a los atribu-
tos de la clase, siempre y cuando ambos estén definidos dentro de la misma
clase.
1 /∗ Clase de prueba para Parvulo3 . Se crea e l o b j e t o ” parvulo ” instanciado
2 de l a c l a s e Parvulo3 y se l e envian cuatro mensajes .
3 @autor Ricardo Ruiz Rodriguez
4 ∗/
5 public class PruebaParvulo3{
6 public static void main ( String [ ] args ) {
7 Parvulo3 parvulo = new Parvulo3 () ;
8
9 System . out . p r i n t l n ( ”Nombre del parvulo : ” + parvulo . obtenNombre () ) ;
10 parvulo . estableceNombre ( ” Ricardo ” ) ;
11 System . out . p r i n t l n ( ”Nombre del parvulo : ” + parvulo . obtenNombre () ) ;
12 parvulo . mensaje () ;
13 }
14 }
Ejemplo 2.6: Clase de prueba para la clase Parvulo3
Los métodos de tipo set sólo deben trabajar sobre un atributo, por lo
que habitualmente sólo reciben un argumento, mismo que corresponde con
la clase (tipo) del atributo a modificar2
.
De manera análoga, los métodos de tipo get no reciben ningún tipo de
argumentos, y la clase de objetos que regresan, está directamente relacionada
con la clase del atributo al que accederán 3
.
Es importante hacer notar también que la clase Parvulo4, a diferencia
de las anteriores, establece ya una caracterı́stica representada y definida por
el atributo nombre, de tal forma que los objetos derivados de ella (párvu-
los4
), compartirán dicha caracterı́stica, aunque cada uno poseerá su propia
identidad (nombre).
2
String para el caso del Ejemplo 2.5.
3
Ídem.
4
Un párvulo es un niño pequeño en edad preescolar.

44. 2.1. MENSAJES Y MÉTODOS 21
Figura 2.3: Salida del Ejemplo 2.6
El Ejemplo 2.6 muestra la clase de prueba para la clase Parvulo3. Al igual
que en los ejemplos anteriores para las clases de prueba, observe que en la
lı́nea 7 se define y crea el objeto parvulo.
Las lı́neas 9 y 11 hacen uso del método obtenNombre a través del envı́o
del mensaje correspondiente, mientras que la lı́nea 10 envı́a el mensaje esta-
bleceNombre con un argumento especı́fico. Finalmente, la lı́nea 12 muestra el
envı́o del mensaje mensaje, el cual deberı́a resultarle ya familiar al lector.
La salida del Ejemplo 2.6 se muestra en la Figura 2.3. Observe que ini-
cialmente el atributo nombre del objeto parvulo no está definido, de ahı́ que
se imprima null en la salida estándar, el cual es el valor por omisión en Java
para las referencias a objetos que no han sido instanciadas, es decir, cuando
los objetos todavı́a no existen, y por consiguiente, no han sido inicializados.
2.1.4. Métodos y constructores
Un constructor es un método especial que se invoca implı́citamente cuan-
do se crea el objeto por medio de la cláusula new.
La cláusula new genera la memoria necesaria para representar al objeto
correspondiente, y lo inicializa por medio de un constructor. En este sentido,
puede haber más de una forma de inicializar un objeto y, en consecuencia,
más de un constructor.
El identificador o nombre de los métodos constructores debe coincidir con
el identificador o nombre de la clase que los define, y como puede haber más
de un constructor cuyo identificador es el mismo, la forma de distinguirse
entre sı́, es a través del número y clase o tipo de los argumentos que definen,
constituyendo con ello una forma de polimorfismo comúnmente conocida co-
mo sobrecarga5
. En la creación del objeto, se invoca el constructor que
coincida con el número y tipo de argumentos proporcionados a la cláusula
new.
Las lı́neas 9-11 del Ejemplo 2.7 muestran la definición del constructor
5
La sobrecarga se trata con un poco más de detalle en la Sección 2.1.5.

45. 22 CAPÍTULO 2. PROGRAMACIÓN ORIENTADA A OBJETOS
Parvulo4, observe cómo el nombre del constructor coincide exactamente con
el nombre de la clase. Dicho constructor define un único argumento n, el cual
es un objeto de la clase String.
La inicialización que hace el constructor Parvulo4 consiste únicamente
de la asignación del objeto n al atributo representado por el objeto nombre.
1 /∗ Ejemplo de envio de mensaje e invocacion de metodos ( Version 1.3) .
2 Se agrega un constructor , e l cual define e l estado i n i c i a l del
3 o b j e t o instanciado .
4 @autor Ricardo Ruiz Rodriguez
5 ∗/
6 public class Parvulo4 {
7 private String nombre ;
8
9 Parvulo4 ( String n) {
10 nombre = n ;
11 }
12
13 public void estableceNombre ( String n) {
14 nombre = n ;
15 }
16
17 public String obtenNombre () {
18 return nombre ;
19 }
20
21 public void mensaje ( ) {
22 System . out . p r i n t l n ( ”Mi nombre es ” + obtenNombre () ) ;
23 }
24 }
Ejemplo 2.7: Definición de la clase Parvulo4
Es importante mencionar que la labor de inicialización de un constructor
en particular puede ser un proceso mucho más elaborado que el descrito hasta
ahora, y estará en función directa de las responsabilidades de inicialización
con que se quiera dotar al constructor, e indudablemente también, de la
problemática en particular que se esté resolviendo por medio del objeto en
cuestión.
Los elementos restantes de la clase Parvulo4 han sido previamente abor-
dados en las secciones anteriores.
El Ejemplo 2.8 presenta la clase de prueba para el Ejemplo 2.7. Observe
que a diferencia de los ejemplos anteriores, en la lı́nea 8 se proporciona un
argumento al constructor Parvulo4, lo cual hace que desde la creación del
objeto parvulo, le sea definido un nombre.
Observe también cómo la secuencia de mensajes subsecuentes coincide con
las del Ejemplo 2.6, excepto que en la lı́nea 11 del Ejemplo 2.8, se envı́a el

46. 2.1. MENSAJES Y MÉTODOS 23
Figura 2.4: Salida del Ejemplo 2.8
mensaje estableceNombre al objeto parvulo para ponerle el nombre completo
(con apellidos) al párvulo.
1 /∗ Clase de prueba para Parvulo4 . Se crea e l o b j e t o ” parvulo ” instanciado
2 de l a c l a s e Parvulo4 , se usa e l constructor definido , y se l e envian
3 cuatro mensajes .
4 @autor Ricardo Ruiz Rodriguez
5 ∗/
6 public class PruebaParvulo4{
7 public static void main ( String [ ] args ) {
8 Parvulo4 parvulo = new Parvulo4 ( ” Ricardo ” ) ;
9
10 System . out . p r i n t l n ( ”Nombre del parvulo : ” + parvulo . obtenNombre () ) ;
11 parvulo . estableceNombre ( ” Ricardo Ruiz Rodriguez ” ) ;
12 System . out . p r i n t l n ( ”Nombre del parvulo : ” + parvulo . obtenNombre () ) ;
13 parvulo . mensaje () ;
14 }
15 }
Ejemplo 2.8: Clase de prueba para la clase Parvulo4
Asegúrese de comprender antes de continuar, que la Figura 2.4 muestra
la salida correspondiente a la ejecución del Ejemplo 2.8.
2.1.5. Sobrecarga
La sobrecarga (overload) es un tipo de polimorfismo, que se caracteriza
por la capacidad de poder definir más de un método o constructor con el
mismo nombre (identificador), siendo distinguidos entre sı́ por el número y
la clase (tipo) de los argumentos que se definen.
El Ejemplo 2.9 muestra la sobrecarga de constructores. Note que las lı́neas
8-10 definen el mismo constructor que el del Ejemplo 2.7 excepto por el
nombre, y que se ha añadido o sobrecargado un nuevo constructor (lı́neas 12-
14), el cual recibe tres argumentos que representan el nombre (n), el primer
apellido (a1), y el segundo apellido (a2) de un párvulo.
La sobrecarga de constructores se da porque ambos constructores tiene el
mismo identificador (Parvulo5), pero tienen distinto número de parámetros.
No puede existir sobrecarga para constructores o métodos con el mismo
identificador, y el mismo número o clase (tipo) de parámetros, tiene que

47. 24 CAPÍTULO 2. PROGRAMACIÓN ORIENTADA A OBJETOS
Figura 2.5: Salida del Ejemplo 2.10
haber algo que los distinga entre sı́, ya que en otro caso, habrı́a ambigüedad.
Los métodos restantes del Ejemplo 2.9 ya ha sido comentados con ante-
rioridad.
1 /∗ Ejemplo de envio de mensaje e invocacion de metodos ( Version 1.4) .
2 Se muestra l a sobrecarga de constructores .
3 @autor Ricardo Ruiz Rodriguez
4 ∗/
5 public class Parvulo5 {
6 private String nombre ;
7
8 Parvulo5 ( String n) {
9 nombre = n ;
10 }
11
12 Parvulo5 ( String n , String a1 , String a2 ) {
13 nombre = n + ” ” + a1 + ” ” + a2 ;
14 }
15
16 public void estableceNombre ( String n) {
17 nombre = n ;
18 }
19
20 public String obtenNombre () {
21 return nombre ;
22 }
23
24 public void mensaje ( ) {
25 System . out . p r i n t l n ( ”Mi nombre es ” + obtenNombre () ) ;
26 }
27 }
Ejemplo 2.9: Definición de la clase Parvulo5
La clase de prueba para el Ejemplo 2.9 se muestra en el Ejemplo 2.10,
y es también muy similar a las clases de prueba anteriormente explicadas.
Únicamente cabe resaltar la creación del objeto parvulo en la lı́nea 7, note
que ahora se le proporcionan tres argumentos al constructor, lo cual hace que
el constructor utilizado sea el definido en las lı́neas 12-14 del Ejemplo 2.9.
La salida del Ejemplo 2.10 aparece en la Figura 2.5. Compare dicha salida
con la de la Figura 2.4 y asegúrese de comprender la diferencia.
1 /∗ Clase de prueba para Parvulo5 . Se crea e l o b j e t o ” parvulo ” instanciado
2 de l a c l a s e Parvulo5 mostrando la sobrecarga de constructores .

48. 2.2. HERENCIA 25
3 @autor Ricardo Ruiz Rodriguez
4 ∗/
5 public class PruebaParvulo5{
6 public static void main ( String [ ] args ) {
7 Parvulo5 parvulo = new Parvulo5 ( ” Ricardo ” , ”Ruiz” , ” Rodriguez ” ) ;
8
9 System . out . p r i n t l n ( ”Nombre del parvulo : ” + parvulo . obtenNombre () ) ;
10 parvulo . estableceNombre ( ” Ricardo ” ) ;
11 System . out . p r i n t l n ( ”Nombre del parvulo : ” + parvulo . obtenNombre () ) ;
12 parvulo . mensaje () ;
13 }
14 }
Ejemplo 2.10: Clase de prueba para la clase Parvulo5
2.2. Herencia
Todos los conceptos del paradigma orientado a objetos discutidos en el
Capı́tulo 1 son importantes, pero el concepto de herencia es uno de los más
importantes, ya que dicho mecanismo de abstracción permite la reutilización
de código de una manera sumamente conveniente, y habilita las capacidades
del polimorfismo a través de la sobre escritura de métodos.
2.2.1. Abstracción
La descripción del concepto de herencia estará basado en los Ejemplos
2.11 y 2.12, pero para poder describirlos, considero pertinente presentar pri-
mero en un diagrama, los detalles de la relación que se quiere ejemplificar
para elevar el nivel de abstracción, es decir, a la forma en que las personas
comprendemos y analizamos las cosas, para posteriormente profundizar con
más conocimiento de causa, en los detalles de la implementación del concepto
en un lenguaje de programación.
El diagrama de clases UML6
del que partirá el análisis se muestra en la
Figura 2.6.
Los detalles completos de la explicación de un diagrama de clases UML
quedan fuera de los alcances de este libro, y sólo se describirán los aspectos
más relevantes que ayuden al lector a visualizar de mejor manera la herencia,
en caso de que el lector no cuente con experiencia en UML.
6
Leguaje de Modelado Unificado (Unified Modeling Language).

49. 26 CAPÍTULO 2. PROGRAMACIÓN ORIENTADA A OBJETOS
Figura 2.6: Diagrama de clases UML para la relación de herencia entre Cien-
tifico y Persona
Un diagrama de clases UML está compuesto, grosso modo, por clases y
las relaciones entre dichas clases. Por otro lado, cada clase es un recuadro
dividido en tres partes:
1. Identificador de la clase.
2. Listado de atributos con la especificación de su clase (tipo) y sus niveles
de acceso correspondientes.
3. Listado de métodos con la especificación de la clase (tipo) de sus ar-
gumentos y valor de retorno, ası́ como los niveles de acceso correspon-
dientes para los métodos.
Tanto para el caso de los atributos como para el de los métodos, los niveles
de acceso están representados por un signo de más para un acceso público
(+), y un signo de menos para un acceso privado (-).
En base a lo anterior, puede observarse de la Figura 2.6 que la clase
Persona, y por lo tanto las instancias que se deriven de ella, tendrán las
siguientes caracterı́sticas (atributos) comunes a una persona: un nombre, una
edad, y una nacionalidad7
. Observe también que se ha definido un conjunto
de operaciones, acciones, responsabilidades o comportamiento comunes a una
persona, definido por los métodos.
7
Podrı́an definirse mucho más caracterı́sticas, o caracterı́sticas diferentes a las descritas,
pero no es la intención del ejemplo representar las caracterı́sticas completas y comunes a
una persona, y lo mismo ocurre para el comportamiento o las responsabilidades represen-
tadas en los métodos.

50. 2.2. HERENCIA 27
Caracterı́sticas más caracterı́sticas menos, acciones más, acciones menos,
es posible decir que una persona en promedio está en general representada
por la clase Persona.
Ahora bien, un cientı́fico es8
una persona, y por lo tanto comparte las
caracterı́sticas y las acciones inherentes a una persona, y es precisamente
esta relación de compartir, la que se refiere a la herencia, ya que se dice que
en la herencia, una clase hereda (comparte) los atributos (caracterı́sticas) y
métodos (acciones) a otra.
La herencia en UML se representa por medio de una flecha como la de la
Figura 2.6, y es importante señalar que el sentido de la flecha es muy impor-
tante, ya que tal y como aparece en la figura, indica que la clase Cientifico
hereda las caracterı́sticas y el comportamiento de la clase Persona (y no al
revés).
Note que la clase Cientifico define un atributo adicional (especialidad),
mismo que se añade a todos los atributos que implı́citamente ya tiene, los
cuales fueron heredados de la clase Persona. Observe también que se han de-
finido cuatro métodos para la clase Cientifico, los cuales tienen las siguientes
caracterı́sticas:
estableceEspecialidad : es un método set para el atributo especialidad
definido en la clase Cientifico.
obtenEspecialidad : es un método get para el atributo especialidad defi-
nido en la clase Cientifico.
mensaje : este método ya estaba definido en la clase Persona, pero al ser
redefinido en la clase Cientifico, se dice que sobre escribe (override) al
primero, lo cual significa que un objeto instanciado de la clase Cien-
tifico, responderá al mensaje mensaje con la definición de su propio
método, y no con la definición del método mensaje definido en la clase
Persona.
mensajeEspecial : este es un nuevo método particular y especı́fico a las
instancias derivadas de la clase Cientifico.
Es sumamente importante que el lector se asegure de comprender la
descripción hasta aquı́ realizada respecto a las clases Persona y Cientifi-
co, ası́ como de entender la relación existente entre ellas antes de continuar
8
Recuerde la idea de división en especializaciones (relación is-a) presentada en el
Capı́tulo 1.

51. 28 CAPÍTULO 2. PROGRAMACIÓN ORIENTADA A OBJETOS
a la siguiente sección, en donde se abordarán los aspectos relacionados con
la implementación.
2.2.2. Implementación
El Ejemplo 2.11 muestra la implementación en Java de la clase Persona
mostrada en la Figura 2.6. Todos los detalles de la clase Persona del Ejemplo
2.11 ya han sido discutidos con anterioridad, por lo que es importante que
el lector los revise, analice, y compare, con los elementos del diagrama UML
descritos en la sección anterior, y que se asegure de comprender la relación
que existe entre ellos.
1 /∗ Ejemplo de herencia .
2 La c l a s e Persona sera l a c l a s e padre ( super c l a s e )
3 de l a c l a s e C i e n t i f i c o .
4 @autor Ricardo Ruiz Rodriguez
5 ∗/
6 public class Persona {
7 // Atributos de l a c l a s e
8 private String nombre ;
9 private int edad ;
10 private String nacionalidad ;
11
12 // Constructor de un argumento ( nombre )
13 Persona ( String n) {
14 nombre = n ;
15 }
16
17 // Constructor de dos argumentos ( nombre y edad )
18 Persona ( String n , int e ) {
19 nombre = n ;
20 edad = e ;
21 }
22
23 // Constructor de t r e s argumentos (nombre , edad y nacionalidad )
24 Persona ( String n , int e , String nac ) {
25 nombre = n ;
26 edad = e ;
27 nacionalidad = nac ;
28 }
29
30 // Metodo para e s t a b l e c e r ( s e t ) e l a t r i b u t o ”nombre”
31 public void estableceNombre ( String n) {
32 nombre = n ;
33 }
34
35 // Metodo para obtener ( get ) e l a t r i b u t o ”nombre”
36 public String obtenNombre () {
37 return nombre ;
38 }
39
40 // Metodo para e s t a b l e c e r ( s e t ) e l a t r i b u t o ”edad”

52. 2.2. HERENCIA 29
41 public void estableceEdad ( int e ) {
42 edad = e ;
43 }
44
45 // Metodo para obtener ( get ) e l a t r i b u t o ”edad”
46 public int obtenEdad () {
47 return edad ;
48 }
49
50 // Metodo para e s t a b l e c e r ( s e t ) e l a t r i b u t o ” nacionalidad ”
51 public void estableceNacionalidad ( String n) {
52 nacionalidad = n ;
53 }
54
55 // Metodo para obtener ( get ) e l a t r i b u t o ” nacionalidad ”
56 public String obtenNacionalidad ( ) {
57 return nacionalidad ;
58 }
59
60 // Metodo para imprimir un mensaje en la s a l i d a estandar
61 public void mensaje ( ) {
62 System . out . p r i n t l n ( ”Puedo hablar , mi nombre es ” + obtenNombre () ) ;
63 }
64
65 // Metodo que simula l a accion de comer por parte de una persona
66 public void comer () {
67 System . out . p r i n t l n ( ”M
m
m
m
m
m uno de l o s p l a c e r e s de la vida . . . ” ) ;
68 }
69 }
Ejemplo 2.11: Definición de la clase Persona
Por otro lado, el Ejemplo 2.12 contiene la implementación de la clase
Cientifico mostrada en la Figura 2.6. Observe que la herencia es implemen-
tada en Java a través del uso de la cláusula extends (lı́nea 6), seguida de la
clase de la que se hereda (Persona) en la definición de la clase Cientifico.
Es importante que el lector note el uso de la cláusula super en los cons-
tructores (lı́neas 11 y 18). El uso en Java de dicha cláusula sólo puede hacerse
en el contexto de constructores, y sirve para delegarle al constructor corres-
pondiente de la clase padre, los detalles de inicialización del objeto en cuestión
que, para el caso de la clase Cientifico, corresponden a los constructores de
dos y tres argumentos de la clase Persona. Asegúrese de comprender ésto
antes de continuar.
Al igual que antes, se deja como ejercicio de análisis para el lector, tanto
los detalles restantes de implementación de la clase Cientifico, como el asegu-
rarse de comprender la relación del diagrama UML con el código del Ejemplo
2.12.

53. 30 CAPÍTULO 2. PROGRAMACIÓN ORIENTADA A OBJETOS
En este punto, es importante también que el lector ponga especial aten-
ción en los métodos mensaje del Ejemplo 2.11 (lı́neas 61-63), y del Ejemplo
2.12 (lı́neas 33-35), ya que serán fundamentales para comprender la sobre es-
critura de métodos que se discute más adelante en la clase de prueba (Ejemplo
2.13).
1 /∗ Ejemplo de herencia .
2 La c l a s e C i e n t i f i c o hereda l a s c a r a c t e r i s t i c a s ( a t r i b u t o s )
3 y operaciones ( metodos ) de l a c l a s e Persona .
4 @autor Ricardo Ruiz Rodriguez
5 ∗/
6 public class C i e n t i f i c o extends Persona {
7 private String e s p e c i a l i d a d ;
8
9 // Constructor de t r e s argumentos (nombre , edad y e s p e c i a l i d a d )
10 C i e n t i f i c o ( String n , int e , String esp ) {
11 super (n , e ) ;
12 e s p e c i a l i d a d = esp ;
13 }
14
15 // Constructor de cuatro argumentos (nombre , edad ,
16 // nacionalidad y e s p e c i a l i d a d )
17 C i e n t i f i c o ( String n , int e , String nac , String esp ) {
18 super (n , e , nac ) ;
19 e s p e c i a l i d a d = esp ;
20 }
21
22 // Metodo para e s t a b l e c e r ( s e t ) e l a t r i b u t o ” e s p e c i a l i d a d ”
23 public void e s t a b l e c e E s p e c i a l i d a d ( String e ) {
24 e s p e c i a l i d a d = e ;
25 }
26
27 // Metodo para obtener ( get ) e l a t r i b u t o ” e s p e c i a l i d a d ”
28 public String obtenEspecialidad () {
29 return e s p e c i a l i d a d ;
30 }
31
32 // Metodo para imprimir un mensaje en la s a l i d a estandar
33 public void mensaje ( ) {
34 System . out . p r i n t l n ( ”Yo, ” + obtenNombre ( ) + ” , soy ” +
obtenEspecialidad () ) ;
35 }
36
37 // Metodo para imprimir un mensaje e s p e c i a l en l a s a l i d a estandar
38 public void mensajeEspecial () {
39 System . out . p r i n t l n ( ”La d i s t a n c i a del s o l a la t i e r r a es 149 600 000
kms” ) ;
40 }
41 }
Ejemplo 2.12: Definición de la clase Cientifico
La clase de prueba para la herencia se presenta en el Ejemplo 2.13 y
se describe a continuación. La lı́nea 10 define el objeto persona y genera

54. 2.2. HERENCIA 31
Figura 2.7: Salida del Ejemplo 2.13
una instancia de la clase Persona con caracterı́sticas especı́ficas; note que
el constructor que está siendo utilizado es el definido en las lı́neas 24-28 del
Ejemplo 2.11.
Observe cómo en las lı́neas 13, 15, 19 y 21 del Ejemplo 2.13, se envı́an
mensajes especı́ficos al objeto persona para obtener su nombre, cambiarle el
nombre, volver a obtener su nombre, solicitarle comer y un mensaje respec-
tivamente; cuya salida se ve expresada en las primeras cuatro lı́neas de la
Figura 2.7.
Por otro lado, la lı́nea 26 define y crea el objeto cientifico como una
instancia de la clase Cientifico. Al igual que antes, note cómo el constructor
utilizado es el definido en las lı́neas 17-20 del Ejemplo 2.12.
A su vez, las lı́neas 28 y 30 del Ejemplo 2.13, realizan algo semejante
a lo que se hizo con el objeto persona, es decir, envı́an mensajes al objeto
cientifico para obtener y cambiar el nombre del cientı́fico respectivamente.
La lı́nea 32 por su parte, cambia la especialidad del cientı́fico a través de
un mensaje de tipo set.
Finalmente, las lı́neas 34, 36, 38 y 40, envı́an mensajes especı́ficos al
objeto cientifico para obtener su nombre y solicitarle comer, un mensaje
y un mensaje especial respectivamente. Note cómo para el mensaje mensaje,
las respuestas del objeto persona y el objeto cientifico difieren por completo,
debido a que aunque el mensaje es el mismo, el objeto que los recibe responde
de manera distinta a dicho mensaje; ésto último fue lo que en el Capı́tulo 1
se definió como polimorfismo9
.
La salida del Ejemplo 2.13 se muestra en la Figura 2.7.
9
El polimorfismo está expresado en el ejemplo en su forma de sobre escritura (override)
de métodos.

55. 32 CAPÍTULO 2. PROGRAMACIÓN ORIENTADA A OBJETOS
1 /∗ Clase de prueba para l a herencia .
2 se l e envian mensajes . Posteriormente se crea e l o b j e t o ”persona”
3 instanciado de l a c l a s e C i e n t i f i c o y tambien se l e envian mensajes ,
4 note que algunos mensajes son heredados de l a super c l a s e .
5 @autor Ricardo Ruiz Rodriguez
6 ∗/
7 public class PruebaHerencia {
8 public static void main ( String [ ] args ) {
9 // Se crea e l o b j e t o ”persona” instanciado de l a c l a s e Persona
10 Persona persona = new Persona ( ” Ricardo ” , 38 , ”Mexicano” ) ;
11
12 // Se imprime e l nombre del o bjeto ”persona” a traves de un mensaje
13 System . out . p r i n t l n ( ”Nombre : ” + persona . obtenNombre () ) ;
14 // Se e s t a b l e c e un nuevo nombre para e l o b j e t o ”persona”
15 persona . estableceNombre ( ” Ricardo Ruiz Rodriguez ” ) ;
16 // Se s o l i c i t a nuevamente a l o b j e t o ”persona” imprimir su nombre
17 System . out . p r i n t l n ( ”Nombre : ” + persona . obtenNombre () ) ;
18 // Se l e envia a l o b j e t o ”persona” e l mensaje ”comer”
19 persona . comer ( ) ;
20 // Se l e envia a l o b j e t o ”persona” e l mensaje ”mensaje”
21 persona . mensaje ( ) ;
22
23 System . out . p r i n t l n ( ) ;
24
25 // Se crea e l o b j e t o ” c i e n t i f i c o ” instanciado de l a c l a s e C i e n t i f i c o
26 C i e n t i f i c o c i e n t i f i c o = new C i e n t i f i c o ( ” Carl Sagan” , 62 ,
” Estadounidense ” , ”Astronomo” ) ;
27 // Se imprime e l nombre del o b j e t o ” c i e n t i f i c o ” a traves de un mensaje
28 System . out . p r i n t l n ( ”Nombre : ” + c i e n t i f i c o . obtenNombre () ) ;
29 // Se e s t a b l e c e un nuevo nombre para e l o b j e t o ” c i e n t i f i c o ”
30 c i e n t i f i c o . estableceNombre ( ” Carl Edward Sagan” ) ;
31 // Se e s t a b l e c e una nueva e s p e c i a l i d a d para e l o b j e t o ” c i e n t i f i c o ”
32 c i e n t i f i c o . e s t a b l e c e E s p e c i a l i d a d ( ”Astronomo y A s t r o f i s i c o ” ) ;
33 // Se s o l i c i t a nuevamente a l o b j e t o ” c i e n t i f i c o ” imprimir su nombre
34 System . out . p r i n t l n ( ”Nombre : ” + c i e n t i f i c o . obtenNombre () ) ;
35 // Se l e envia a l o b j e t o ” c i e n t i f i c o ” e l mensaje ”comer”
36 c i e n t i f i c o . comer ( ) ;
37 // Se l e envia a l o b j e t o ” c i e n t i f i c o ” e l mensaje ”mensaje”
38 c i e n t i f i c o . mensaje ( ) ;
39 // Se l e envia a l o b j e t o ” c i e n t i f i c o ” e l mensaje ” mensajeEspecial ”
40 c i e n t i f i c o . mensajeEspecial ( ) ;
41 // persona . mensajeEspecial () ;
42 }
43 }
Ejemplo 2.13: Clase de prueba para la herencia

56. 2.3. CONSIDERACIONES FINALES 33
2.3. Consideraciones finales
2.3.1. Respecto al envı́o de mensajes
La sintaxis general en Java para el envı́o de mensajes a un objeto es la
siguiente:
objeto.mensaje(lista de argumentos)
donde objeto es un objeto de una clase previamente definida, y mensaje es uno
de los métodos públicos definidos para dicha clase. La lista de argumentos es
una lista de argumentos separada por comas, en donde cada argumento puede
ser un objeto, o un tipo de dato primitivo.
2.3.2. Respecto a la sobrecarga de operadores
Algunos lenguajes de programación soportan un concepto relacionado con
sobrecarga de operadores. La idea general del concepto de sobrecarga se ha
planteado en la Sección 2.1.5. El lenguaje de programación Java no soporta
la sobrecarga de operadores, y por consiguiente, se ha omitido su descripción;
pero es importante que el lector conozca que el concepto de sobrecarga no es
exclusivo de los métodos o constructores, y mucho menos de un lenguaje de
programación en particular.
2.3.3. Respecto al paradigma
El establecimiento de niveles de acceso como private para los atributos
de una clase, y el uso de métodos de tipo set y get están directamente rela-
cionados con el principio de ocultación de información.
Ahora bien, es probable que el lector haya notado que en la descripción del
Ejemplo 2.13, en distintas ocasiones se hizo referencia a los objetos persona y
cientifico como si fueran en sı́ mismos personas o entidades existentes. Ésto
se hizo de manera deliberada, ya que como se comentó en el Capı́tulo 1,
el paradigma orientado a objetos eleva el nivel de abstracción, y hace que
se haga referencia a las entidades fundamentales del paradigma (objetos),
como elementos comunes de nuestro lenguaje natural, lo cual permite que los
problemas se puedan expresar de una manera más natural e intuitiva.
En éste sentido, al dotar a los objetos de una personalidad propia con
caracterı́sticas y responsabilidades, en lugar de pensar en términos de datos,

57. 34 CAPÍTULO 2. PROGRAMACIÓN ORIENTADA A OBJETOS
variables, y funciones o procedimientos que operen sobre dichos datos, se
eleva el nivel de abstracción, facilitando ası́ el análisis y la comprensión, ya
que el problema y su solución pueden ser expresados y analizados en términos
del dominio del problema, y no en el del medio (lenguaje de programación) de
la solución. Ésta es la forma en la que las personas abstraemos y utilizamos
la información.
Es sumamente importante que el lector tenga presente, que en el paradig-
ma orientado a objetos, no se piensa en términos de datos, sino en términos
de entidades con caracterı́sticas y responsabilidades especı́ficas, por lo que,
cuando defina una clase, puede resultarle útil el plantearse al menos un par
de preguntas10
que le permitan determinar si los los objetos derivados de su
clase tienen o no sentido, además de una alta cohesión:
¿Los atributos representan caracterı́sticas o propiedades, o definen un
estado para los objetos que serán instanciados?
¿La clase representa en sus métodos servicios, comportamiento, accio-
nes o responsabilidades inherentes a los objetos que deriven de ella?
Con estas dos sencillas preguntas, además de validar y verificar su diseño
de clases, estará reforzando el concepto de encapsulamiento.
10
Las preguntas propuestas son sólo una guı́a y una sugerencia al lector, no pretenden
ser de ninguna manera una lista completa y absoluta.

58. 2.4. EJERCICIOS 35
2.4. Ejercicios
1. En el Ejemplo 2.5 se hizo referencia a la invocación del mensaje ob-
tenNombre (lı́nea 17) dentro del método mensaje. Cambie el método
obtenNombre por el atributo nombre y compruebe lo descrito en el
texto.
2. Considere el Ejemplo 2.6. ¿Qué sucede si en lugar de acceder al atributo
nombre por medio del método obtenNombre (lı́neas 9 y 11) se intenta
acceder directamente al atributo a través del operador punto?.
Para probar lo anterior, cambie la expresión:
parvulo.obtenNombre()
por la expresión:
parvulo.nombre
recompile y analice lo que suceda.
3. Modifique el Ejemplo 2.6 para que genere más de un objeto de la clase
Parvulo3 del Ejemplo 2.5, de tal forma que tenga un conjunto de al
menos tres párvulos.
Para los objetos creados, definales una identidad a cada uno de los
párvulos instanciados por medio de la asignación de un nombre distinto
a cada uno de ellos, envı́eles mensajes, experimente y juegue con ellos,
recuerde que sus objetos son, al fin y al cabo, niñ@s pequeñ@s.
4. Para el Ejemplo 2.7, defina y añada un constructor sin argumentos, de
tal forma que la labor del constructor sea definir su propio nombre (el
nombre del lector) al atributo nombre.
Modifique en consecuencia la clase del Ejemplo 2.8 para que haga uso
del constructor recién definido, y compruebe su funcionamiento.
5. La Sección 2.1.5 abordó el tema de la sobrecarga, y ejemplificó el con-
cepto utilizando sobrecarga de constructores. La sobrecarga de métodos
es análoga a la de constructores.

59. 36 CAPÍTULO 2. PROGRAMACIÓN ORIENTADA A OBJETOS
Modifique el Ejemplo 2.9 para que implemente la sobrecarga de méto-
dos de la siguiente manera:
a) Defina un nuevo método con la siguiente firma:
public void mensaje(String m)
b) La responsabilidad del nuevo método mensaje, será la de imprimir
en la salida estándar la leyenda “Mensaje recibido”, seguido de la
cadena m.
c) Realice una clase de prueba (puede basarse en la del Ejemplo
2.10) para comprobar el funcionamiento de todos los métodos,
especialmente, el método sobrecargado mensaje.
6. Considere el Ejemplo 2.9 y modifı́quelo para que, en lugar de uno,
defina tres atributos:
nombre (String).
apellido1 (String).
apellido2 (String).
En base a lo anterior:
a) Agregue el método set correspondiente para cada uno de los atri-
butos, en base a lo descrito en el texto.
b) Agregue el método get correspondiente para cada uno de los atri-
butos, también en base a lo descrito en el texto.
c) Agregue un constructor para que sea posible construir un objeto
(párvulo) utilizando únicamente el nombre, y el primer apellido.
d) Modifique el método mensaje para que, en caso de que alguno de
los atributos del objeto en cuestión sea null, dicho atributo sea
ignorado y en consecuencia, no se imprima en la salida estándar.
e) Construya una clase de prueba que demuestre tanto el funciona-
miento de todas las posibles opciones de construcción de objetos,
como el adecuado funcionamiento de los métodos set, get y men-
saje.

60. 2.4. EJERCICIOS 37
7. El Ejemplo 2.13 tiene la lı́nea 41 comentada, por lo que el compilador
y la JVM la ignoran. Si la descomenta ¿qué piensa que sucederá?,
¿compilará?, ¿se ejecutará?, ¿imprimirá algo en la salida estándar?,
¿fallará la ejecución?.
Después de analizar el programa, responda dichas preguntas, y corro-
bore su respuesta con la experimentación.
8. Modifique el Ejemplo 2.11 para que contenga más atributos, es decir,
para que las caracterı́sticas de una persona estén más completas. No
olvide agregar métodos de tipo set y get por cada uno de los atributos
que añada.
Para los atributos, añada al menos los siguientes cambios:
Cambie el atributo nombre por una distribución más convencional:
nombre, primer apellido, y segundo apellido.
Agregue un atributo que represente la dirección o domicilio.
Agregue un atributo que represente el sexo, femenino o masculino,
según sea el caso.
Después de lo anterior:
a) Compruebe el adecuado funcionamiento de la clase Persona res-
pecto de las modificaciones recién hechas. Asegúrese de comprobar
que los métodos set y get trabajan de la manera esperada.
b) Compruebe que con los cambios realizados a la clase Persona, los
aspectos relacionados con la herencia de la clase Cientifico del
Ejemplo 2.12, siguen funcionando sin ningún tipo de problema.
c) Modifique la clase Cientifico de manera análoga, y compruebe
también que el mecanismo de la herencia permanece inalterado.
Para la clase Cientifico agregue dos atributos (y sus correspon-
dientes métodos de acceso):
1) Institución o lugar donde labora.
2) Grado de estudios.
d) Agregue nuevas acciones, comportamientos o responsabilidades a
las clases Persona y Cientifico, y asegúrese de probar su adecua-
do funcionamiento. No olvide experimentar con los conceptos de
sobrecarga y sobre escritura.

61. 38 CAPÍTULO 2. PROGRAMACIÓN ORIENTADA A OBJETOS
9. Construya un ejemplo completamente diferente al visto en el texto,
donde ponga de relieve los conceptos de envı́o de mensajes, herencia,
polimorfismo, encapsulamiento y ocultación de información.
Para realizar lo anterior, puede apoyarse de la jerarquı́a de clases de la
Figura 1.2, o de alguna otra figura o idea que sea de su preferencia.

62. Capı́tulo 3
Estructuras de datos
Ask not what you can do to your data structures, but rather ask
what your data structures can do for you.
3.1. Panorama general
De manera general, es posible decir que una computadora es una máquina
que manipula y procesa datos.
Las estructuras de datos están relacionadas con el estudio de cómo es que
se organizan los datos dentro de una computadora, y de cómo se manipulan,
procesan y emplean dichos datos, para representar información que sea de
utilidad para las personas.
Existen muchos tipos de estructuras de datos, y para cada estructura de
datos, hay diferentes variaciones que las particularizan para un contexto de
uso especı́fico.
Un tratado amplio y completo de las estructuras de datos, queda fuera
de los alcances de este libro, por lo que sólo se mencionarán algunas de las
estructuras de datos más comunes y convencionales, ası́ como algunas de sus
variaciones.
A continuación se presenta una descripción muy general de las estructuras
de datos que se analizarán en los capı́tulos siguientes:
Pilas : son estructuras de datos ampliamente utilizadas y sumamente im-
portantes en compiladores y sistemas operativos por ejemplo. En una
pila, las inserciones y las eliminaciones se efectúan únicamente en un
extremo de la estructura de datos: su parte superior.
39

63. 40 CAPÍTULO 3. ESTRUCTURAS DE DATOS
Colas de espera : este tipo de estructuras de datos representan en general
lı́neas de espera; las inserciones se efectúan en la parte posterior de la
misma, y las eliminaciones se hacen por la parte delantera.
Listas enlazadas : son colecciones de elementos de datos alineados en una
fila. En una lista enlazada, las inserciones y las eliminaciones se efectúan
en cualquier parte de la estructura de datos.
Árboles binarios : son estructuras de datos que facilitan la búsqueda, la
clasificación u ordenamiento de los datos a alta velocidad, la elimina-
ción de elementos duplicados, la representación de sistemas de archivos
y directorios, y las expresiones de compilación entre otras muchas apli-
caciones.
Cada una de estas estructuras de datos tienen muchas otras, y muy in-
teresantes aplicaciones, algunas de las cuales, se presentan y discuten en los
capı́tulos correspondientes a cada una de ellas.
3.2. Tipos de datos y referencias
Probablemente el lector esté familiarizado con el concepto de tipo de
dato, ya sea debido a que tenga experiencia previa con algún lenguaje de
programación, o simplemente porque ha revisado el material del Apéndice A
o del Capı́tulo 2. Entonces ¿podrı́a definir qué es un tipo de dato?.
Un tipo de dato es un método para interpretar un patrón de bits. En
éste sentido, una secuencia de bits determinada podrı́a ser interpretada de
una forma u otra, en función del tipo de dato.
En la mayorı́a de los lenguajes de programación, el programador especifi-
ca, mediante las declaraciones de variables u objetos, cómo es que el programa
va a interpretar el contenido de la memoria de la computadora.
Las declaraciones también le especifican al compilador exactamente, qué es
lo que representan los sı́mbolos de las operaciones que se utilizarán, ya que
aunque en apariencia es lo mismo, los mecanismos de implementación de una
operación aritmética tan aparentemente simple como la adición, difieren de
un tipo de dato a otro.
Por otro lado, para la mayorı́a de los lenguajes de programación, los
nombres de variables o identificadores asociados a los objetos, son en reali-
dad referencias, es decir, direcciones de memoria en las que se almacenan
fı́sicamente los objetos a los que hacen referencia.

64. 3.3. TIPOS DE DATOS ABSTRACTOS (ADT) 41
El manejo de referencias o direcciones de memoria puede ser explı́cito,
como en el caso de los lenguajes C y C++ por ejemplo, donde el manejo
de referencias se realiza a través de apuntadores. En algunos otros lenguajes
como Java y C#, el manejo de referencias es implı́cito, es decir, se realiza a
través del nombre o identificador de los objetos.
Tanto el manejo de referencias explı́cito como el implı́cito, tienen sus
ventajas y desventajas, y las fortalezas de uno, son las debilidades del otro
y viceversa. No es la intención de esta sección ni la del libro extenderse en
dichos aspectos, ya que para los objetivos especı́ficos que se persiguen en
este texto, basta con saber que Java hace uso de referencias implı́citas, y que
el nombre los objetos son en realidad dichas referencias y no los objetos en
sı́ mismos. En la Sección 3.4.1 se detalla y ejemplifica el manejo de referencias
para los objetos.
3.3. Tipos de datos abstractos (ADT)
Desde el punto de vista de la programación, es importante que los pro-
gramadores puedan definir sus propias abstracciones de datos, de tal forma
que dichas abstracciones trabajen de manera parecida a las abstracciones o
a las primitivas de datos proporcionadas por el sistema subyacente.
Un tipo de dato abstracto o ADT (Abstract Data Type), es definido
por una especificación abstracta, es decir, permite especificar las propiedades
lógicas y funcionales de un tipo de dato.
Desde el punto de vista de los ADT, un tipo de dato es un conjunto de
valores y un grupo de operaciones definidas sobre dichos valores. El conjunto
de valores y el de las operaciones, forman una estructura matemática que
se implementa usando una estructura de datos particular de hardware o de
software.
El concepto de ADT está relacionado con la concepción matemática que
define al tipo de datos, por lo que, al definir un ADT como concepto ma-
temático, no interesa la eficiencia del espacio o del tiempo1
, sino las pro-
piedades y caracterı́sticas inherentes a él. La definición de un ADT no se
relaciona en lo absoluto con los detalles de la implementación; de hecho, tal
vez ni siquiera sea posible implementar un ADT particular en ningún tipo
de hardware o software2
.
1
Los cuales son aspectos relacionados con la implementación del ADT.
2
Piense por ejemplo en los números reales y en la propiedad de la densidad de los

65. 42 CAPÍTULO 3. ESTRUCTURAS DE DATOS
Un ADT consta de dos partes: una definición de valor y una definición
de operador, mismas que se describen a continuación:
1. La definición del valor establece el conjunto de valores para el ADT,
y consta a su vez de dos partes:
a) Una cláusula de definición.
b) Una cláusula de condición3
.
2. En la definición del operador, cada operador está definido como una
operación abstracta, con condiciones previas opcionales, y las condicio-
nes posteriores o postcondiciones.
Por otro lado, para la implementación de un ADT, es necesario tomar en
cuenta los siguientes aspectos:
1. Hacer disponible (pública) la definición del nuevo tipo.
2. Hacer disponibles un conjunto de operaciones que puedan ser utilizadas
para manipular las instancias del tipo definido (métodos públicos de
servicios).
3. Proteger los datos asociados con el tipo de dato que está siendo definido
(atributos privados), de tal forma que dichos datos sólo puedan ser
accedidos por medio de los métodos proporcionados para ello.
4. Poder generar múltiples instancias del tipo definido, preferentemente,
con más de una opción de inicialización, siempre que ésto no entre en
contradicción con la definición o restricciones del tipo.
Es importante resaltar que, asociado con un ADT particular, puede haber
una o más implementaciones distintas.
En resumen, los ADT son un mecanismo de abstracción sumamente im-
portante y, dado que la programación orientada a objetos (POO) se funda-
menta en la abstracción, es posible decir que constituye uno de los pilares de
la orientación a objetos.
números reales.
3
Para la definición de un ADT racional por ejemplo, una cláusula de condición estarı́a
relacionada con la restricción de que el denominador de un número racional, no puede ser
cero.

66. 3.3. TIPOS DE DATOS ABSTRACTOS (ADT) 43
3.3.1. Especificación del ADT Racional
Existen varios métodos para especificar un ADT, desde notaciones ma-
temáticas, hasta descripciones detalladas hechas en lenguaje natural. Lo im-
portante de la especificación es que sea clara y no ambigüa.
Esta sección hará uso de la notación matemática para la especificación
del ADT racional.
Sea r un número racional. Se define r como el cociente de dos números
enteros, es decir, r = p
q
donde p, q ∈ Z, ∀q = 0.
Las operaciones aritméticas de suma, resta, multiplicación y división de
dos números racionales, se especifica a continuación:
Sean r1 y r2 dos números racionales, es decir: r1, r2 ∈ Q definidos como:
r1 =
p1
q1
; p1, q1 ∈ Z, q1 = 0 (3.1)
r2 =
p2
q2
; p2, q2 ∈ Z, q2 = 0 (3.2)
la suma de r1 y r2 se define de la siguiente manera:
r1 + r2 =
p1
q1
+
p2
q2
=
(p1 ∗ q2) + (q1 ∗ p2)
q1 ∗ q2
(3.3)
y la resta de manera análoga:
r1 − r2 =
p1
q1
−
p2
q2
=
(p1 ∗ q2) − (q1 ∗ p2)
q1 ∗ q2
(3.4)
mientras que la multiplicación está dada por:
r1 ∗ r2 =
p1
q1
∗
p2
q2
=
p1 ∗ p2
q1 ∗ q2
(3.5)
y la división por:
r1
r2
=
p1
q1
p2
q2
=
p1 ∗ q2
q1 ∗ p2
(3.6)
Observe que la especificación de los valores para el ADT racional está dada
por las Ecuaciones 3.1 y 3.2, y que existe una restricción sobre el valor del
denominador representado por q1 y q2 respectivamente.
Finalmente, note que la especificación de las operaciones aritméticas para
el ADT está dada por las Ecuaciones 3.3, 3.4, 3.5 y 3.6.

67. 44 CAPÍTULO 3. ESTRUCTURAS DE DATOS
Figura 3.1: Salida de una ejecución del Ejemplo 3.2 al intentar crear un
número racional cuyo denominador sea cero
3.3.2. Implementación del ADT Racional
El Ejemplo 3.1 muestra una posible implementación de ADT racional
definido en la sección anterior.
Las lı́neas 7 y 8 definen los atributos de un número racional (p
q
). Los
detalles relacionados con los métodos de tipo set y get (lı́neas 25-41), ya han
sido comentados en el Capı́tulo 2 y no se repetirán aquı́.
Por otro lado, los constructores definidos (lı́neas 10-23) requieren de una
ampliación en su explicación, ya que difieren un poco de lo hasta ahora
comentado para los constructores.
El constructor principal o base, es el definido en las lı́neas 18-23. Ob-
serve que dicho constructor recibe dos argumentos, mismos que representan
el numerador (n) y el denominador (d) del número racional que se desea
inicializar. En la lı́nea 19, el constructor realiza una verificación del denomi-
nador (cláusula de condición), de tal forma que si éste es cero, se crea (new)
y lanza (throw) una excepción4
para indicar el error a través de la clase
RuntimeException5
(vea la Figura 3.1).
1 /∗ Ejemplo de ADT.
2 La c l a s e Racional es una abstraccion s e n c i l l a de l o s numeros rac io nal es
3 cuya forma es p / q , donde p y q son numeros enteros .
4 @autor Ricardo Ruiz Rodriguez
5 ∗/
6 public class Racional {
7 private int p ;
8 private int q ;
9
10 Racional () {
11 this (1 , 1) ;
12 }
13
14 Racional ( int n) {
15 this (n , 1) ;
16 }
4
Vea la Sección A.5.5 del Apéndice A.
5
Note también que el mismo comportamiento es considerado en las lı́neas 30 y 31 para
el método estableceDenominador.

68. 3.3. TIPOS DE DATOS ABSTRACTOS (ADT) 45
17
18 Racional ( int n , int d) {
19 i f (d == 0)
20 throw new RuntimeException ( ”El denominador no puede s e r cero . ” ) ;
21 p = n ;
22 q = d ;
23 }
24
25 public void estableceNumerador ( int n) {
26 p = n ;
27 }
28
29 public void estableceDenominador ( int d) {
30 i f (d == 0)
31 throw new RuntimeException ( ”El denominador no puede s e r cero . ” ) ;
32 q = d ;
33 }
34
35 public int obtenNumerador () {
36 return p ;
37 }
38
39 public int obtenDenominador () {
40 return q ;
41 }
42
43 public Racional suma( Racional r ) {
44 Racional s = new Racional ( ) ;
45
46 s . p = p ∗ r . obtenDenominador () + q ∗ r . obtenNumerador () ;
47 s . q = q ∗ r . obtenDenominador () ;
48
49 return s ;
50 }
51
52 public Racional m u l t i p l i c a ( Racional r ) {
53 Racional m = new Racional ( ) ;
54
55 m. p = p ∗ r . obtenNumerador () ;
56 m. q = q ∗ r . obtenDenominador () ;
57
58 return m;
59 }
60
61 public String toString () {
62 return p + ”/” + q ;
63 }
64 }
Ejemplo 3.1: Clase implementa la abstracción de un número racional
Los constructores de las lı́neas 10-12 y 14-16, se apoyan del constructor
base de las lı́neas 18-23 para realizar la inicialización del objeto a través del
uso de la cláusula this. La cláusula this es una referencia que tienen todos
los objetos hacia sı́ mismos, por lo que en el contexto de los constructores,

69. 46 CAPÍTULO 3. ESTRUCTURAS DE DATOS
Figura 3.2: Salida de la ejecución del Ejemplo 3.2
invoca al constructor sobre cargado que corresponda con el tipo y número de
argumentos que envı́a, que para el caso de las lı́neas 11 y 15, corresponden
con el constructor base de las lı́neas 18-23.
La implementación de las Ecuaciones 3.3 y 3.5 aparecen en las lı́neas 43-
50 y 52-59 respectivamente6
. Observe que en las lı́neas 46 y 47 (55 y 56) se
accede directamente a los atributos p y q a través del operador punto (.), es
decir, sin hacer uso de los métodos de acceso set y get; ésto es ası́ debido a que
el objeto s (m) es de la misma clase que define al método suma (multiplica),
por lo que el acceso es concedido7
.
Por otro lado, note también que para el objeto (this) que recibe el mensaje
suma (multiplica), los atributos p y q de las lı́neas 46 y 47 (55 y 56) son
accedidos sin ningún tipo de operador ni mensaje, es decir, son accedidos
por contexto, ya que el objeto que recibe el mensaje conoce cuáles son sus
propios atributos, por lo que dentro del método, la expresión:
p * r.obtenDenominador()
es equivalente a la expresión:
this.p * r.obtenDenominador()
Finalmente, el método toString (lı́neas 61-63) requiere una mención apar-
te, ya que éste método sobre escribe8
y redefine el comportamiento definido
en el método la clase Object del API de Java, y tiene como responsabilidad
el regresar una representación en cadena del objeto.
La clase de prueba del Ejemplo 3.1 es la del Ejemplo 3.2, cuya salida
corresponde a la mostrada en la Figura 3.2.
6
La implementación de las Ecuaciones 3.4 y 3.6 se dejan como ejercicio para el lector.
7
Recuerde lo planteado en el Ejercicio 2 del Capı́tulo 2 y analice la diferencia.
8
Razón por la cual se preservó el nombre del método.

70. 3.4. ABSTRACCIÓN DE ESTRUCTURAS DE DATOS 47
1 /∗ Clase de prueba para Racional . Se crean dos o b j e t o s
2 ( numeros r a c i o n a l e s ) , se suman y m u l t i p l i c a n ( por medio de mensajes ) ,
3 y se presentan l o s r e s u l t a d o s correspondientes .
4 @autor Ricardo Ruiz Rodriguez
5 ∗/
6 public class PruebaRacional {
7 public static void main ( String [ ] args ) {
8 Racional r1 = new Racional (1 , 3) ; // 1/3
9 Racional r2 = new Racional (2 , 5) ; // 2/5
10
11 System . out . p r i n t l n ( ” r1 = ” + r1 ) ;
12 System . out . p r i n t l n ( ” r2 = ” + r2 ) ;
13 System . out . p r i n t l n ( r1 + ” + ” + r2 + ” = ” + r1 . suma( r2 ) ) ;
14 System . out . p r i n t l n ( r1 + ” ∗ ” + r2 + ” = ” + r1 . m u l t i p l i c a ( r2 ) ) ;
15 }
16 }
Ejemplo 3.2: Clase de prueba para la clase Racional
Por último, aunque el Ejemplo 3.2 se explica a sı́ mismo, se resaltarán los
siguientes aspectos:
Las lı́neas 8 y 9 crean los números racionales r1 y r2, donde r1 = 1
3
y
r2 = 2
5
.
Las lı́neas 13 y 14 envı́an los mensajes suma y multiplica respectiva-
mente, al objeto r1. Note que el argumento de ambos métodos es r2,
y que al valor de retorno de dichos métodos (un número racional), les
es enviado de manera implı́cita el mensaje toString para obtener la re-
presentación en cadena de los resultados correspondientes. Ésto último
sucede también con las lı́neas 11 y 12 pero para los objetos r1 y r2.
3.4. Abstracción de estructuras de datos
El estudio de las estructuras de datos implica, en general, dos propósitos
complementarios:
1. Identificar y desarrollar entidades y operaciones útiles relacionadas con
dichas entidades. También es necesario determinar el tipo de problemas
que se solucionan utilizando dichas entidades y operaciones.
2. El segundo es el de determinar representaciones para dichas entidades
abstractas, ası́ como implementar las operaciones abstractas en repre-
sentaciones concretas.

71. 48 CAPÍTULO 3. ESTRUCTURAS DE DATOS
El primero de estos dos propósitos considera a un tipo de datos de alto
nivel como un instrumento que se usa para solucionar otros problemas, y
está en estrecha relación con la definición de tipos de datos abstractos (ADT).
El segundo propósito considera la implementación del tipo de dato o ADT,
como un problema que se va resolver utilizando objetos o elementos existentes
a través de la herencia (relación es (is-a)) o la composición (relación tiene
(has-a)).
Como ya se mencionó con anterioridad, en ocasiones ninguna implemen-
tación tanto de hardware como de software puede modelar por completo un
concepto matemático (un tipo de dato entero o real por ejemplo), por lo
que es importante conocer las limitaciones de una implementación particu-
lar, ya que una consideración fundamental de cualquier implementación es
su eficiencia.
3.4.1. Clases autorreferidas
La implementación de las estructuras de datos de los capı́tulos siguientes,
estará basada en un concepto muy importante: la autorreferencia.
En el contexto de la orientación a objetos, la autorreferencia es la ca-
pacidad que tienen los objetos de una clase de almacenar explı́citamente una
referencia a objetos de su misma clase, es decir, a objetos de su mismo tipo.
Considere el Ejemplo 3.3, el cual muestra una clase autorreferida (Nodo)
con dos atributos:
1. dato: el atributo que representa el elemento a almacenar en el nodo.
2. siguiente: el cual es una referencia a un objeto cuya clase es la misma
que lo define (Nodo), y por lo tanto, es una autorreferencia.
En estructuras de datos, un nodo es la unidad mı́nima de almacenamiento
dentro de la estructura de datos, y puede ser tan simple o elaborada como
se desee.
Para el caso del Ejemplo 3.3, el nodo únicamente almacena enteros primi-
tivos (int), pero como se discutirá más adelante, en el Capı́tulo 4, es posible
representar entidades más elaboradas que un número entero.
Considere la creación de un objeto nodo instanciado de la clase Nodo, y
su correspondiente representación mostrada en la Figura 3.3:
Nodo nodo = new Nodo(1974);

72. 3.4. ABSTRACCIÓN DE ESTRUCTURAS DE DATOS 49
Figura 3.3: Representación de un objeto de la clase Nodo (Ejemplo 3.3)
En la Figura 3.3 puede apreciarse que un objeto es en realidad una re-
ferencia a una entidad con caracterı́sticas definidas por la clase de la que
deriva, que para el caso especı́fico del Ejemplo 3.3, están dadas por los atri-
butos dato y siguiente.
1 /∗ Ejemplo de una c l a s e a u t o r r e f e r i d a .
2 @autor Ricardo Ruiz Rodriguez
3 ∗/
4 public class Nodo{
5 private int dato ;
6 private Nodo s i g u i e n t e ;
7
8 Nodo( int d) {
9 dato = d ;
10 s i g u i e n t e = null ;
11 }
12
13 public void estableceDato ( int d) {
14 dato = d ;
15 }
16
17 public int obtenDato () {
18 return dato ;
19 }
20
21 public void e s t a b l e c e S i g u i e n t e (Nodo n) {
22 s i g u i e n t e = n ;
23 }
24
25 public Nodo obtenSiguiente () {
26 return s i g u i e n t e ;
27 }
28 }
Ejemplo 3.3: Clase autorreferida
Observe la relación entre el Ejemplo 3.3 y la Figura 3.3, y note cómo
en el constructor (lı́neas 8-11) el objeto es inicializado con el valor recibi-
do como argumento, y con null para la referencia siguiente, lo cual ha sido
representado en la figura con una diagonal () para enfatizar que la referen-
cia representada por el atributo siguiente, no hace referencia inicialmente a
ningún otro objeto. Observe también que la clase o tipo del objeto nodo, es

73. 50 CAPÍTULO 3. ESTRUCTURAS DE DATOS
Figura 3.4: Secuencia de nodos generados por una clase autorreferida
la misma que la del atributo siguiente, lo cual constituye la autorreferencia.
Asegúrese de comprender ésto antes de continuar.
3.4.2. Implementación
En base a lo descrito con anterioridad, es posible decir que las estructuras
de datos consisten, de manera general, en un conjunto de nodos ordenados
en una secuencia lógica como la que se muestra en la Figura 3.4.
El mecanismo utilizado para la inserción de nodos en la estructura de
datos, está en función directa de las reglas especificadas por la definición de
la estructura de datos.
Por otro lado, la especificación de las caracterı́sticas de la estructura de
datos se implementará a través de atributos, mientras que la especificación
de las reglas de operación o de comportamiento de la estructura de datos,
será implementada por medio de métodos.
Las estructuras de datos estudiadas en los capı́tulos siguientes, tendrán
en general la forma presentada en la Figura 3.4.
3.5. Consideraciones finales
Las nociones de la programación orientada a objetos son construidas sobre
las ideas de los tipos de datos abstractos.
Un ADT es una abstracción sumamente útil, y está estrechamente re-
lacionada con los principios de la orientación a objetos, ya que puede ser
definida en términos de las caracterı́sticas y los servicios que ofrece.
La importancia más significativa en la idea de los ADT es la separación
de las nociones de interfaz (servicios) e implementación.
La definición y operación de una estructura de datos, está en estrecha
relación con la definición de un ADT, por lo que en los capı́tulos siguientes,

74. 3.5. CONSIDERACIONES FINALES 51
además de definir las estructuras de datos más usuales, se presentará una im-
plementación particular, pero es importante que el lector recuerde que existe
más de una implementación para una definición de un ADT determinado.
Finalmente, además de la implementación de las estructuras de datos, se
presentarán también algunas de las aplicaciones clave más representativas
en el desarrollo de cada una de las estructuras de datos estudiadas, con la
intención de poner en práctica, de manera combinada, tanto los conceptos
orientados a objetos, como los de las estructuras de datos.

75. 52 CAPÍTULO 3. ESTRUCTURAS DE DATOS
3.6. Ejercicios
1. Investigue cómo es que se representan los tipos de datos primitivos en
una computadora.
Es preciso que conozca cómo se representa un tipo de datos int por
ejemplo, ¿cuátos bytes le son asignados a un entero?.
Los números de punto flotante (float y double por ejemplo), también
tiene una representación particular dentro de una computadora basada
en los conceptos de mantisa y exponente. Investigue dichos conceptos,
ası́ como la representación fı́sica de los tipos de datos en una compu-
tadora convencional.
2. Modifique el Ejemplo 3.2 para que genere una salida como la de la Fi-
gura 3.1. Asegúrese de probar el caso de error tanto para el constructor,
como para el método estableceDenominador.
3. Considere el Ejemplo 3.1, ¿qué valor inicial tiene el objeto Racional s
y m en las lı́neas 44 y 53 respectivamente?.
4. Modifique el Ejemplo 3.1 para que, en lugar de acceder directamente
a los atributos p y q de los objetos s y m (lı́neas 46-47 y 55-56 res-
pectivamente), se acceda a ellos y se modifiquen sus correspondientes
valores a través del método set correspondiente.
5. En base a lo descrito en el texto, modifique el Ejemplo 3.1 para que
cambie la sentencia (lı́nea 46):
s.p = p * r.obtenDenominador() + q * r.obtenNumerador();
por:
s.p = this.p * r.obtenDenominador() +
this.q * r.obtenNumerador();
Realice lo correspondiente para las lı́neas 47, 55 y 56 respectivamente.

76. 3.6. EJERCICIOS 53
6. El Ejemplo 3.1 implementa las operaciones de adición (suma) y multi-
plicación (multiplica). Para que la implementación sea completa, imple-
mente las operaciones aritméticas faltantes de sustracción y división,
llámeles resta y divide respectivamente, y ajústese a la especificación
de las Ecuaciones 3.10 y 3.12 respectivamente.
7. Además de lo desarrollado en el ejercicio anterior, piense en cómo me-
jorar la definición del ADT racional discutido en el texto. Tome en
cuenta, al menos, los siguientes aspectos:
Comparación de igualdad: ¿cuándo se dice que dos números ra-
cionales son iguales?. Ejemplo:
3
21
≡
1
7
(3.7)
Simplificación: simplificar a su expresión mı́nima un número ra-
cional, ya sea como resultado de una operación, o simplemente
como utilidad. Ejemplo:
3
21
⇒
1
7
(3.8)
Investigue la definición y forma de dichos aspectos, analı́celos e im-
pleméntelos para completar y mejorar el Ejemplo 3.1.
8. Considere las siguientes definiciones para los números complejos:
Sean c1 y c2 dos números complejos es decir: c1, c2 ∈ C definidos de la
siguiente manera:
c1 = (a + bi) y c2 = (c + di)
donde a, b, c, d ∈ R.
La suma de c1 y c2 se define como:
c1 + c2 = (a + bi) + (c + di) = (a + c) + (b + d)i (3.9)
y la resta de manera análoga:
c1 − c2 = (a + bi) − (c + di) = (a − c) + (b − d)i (3.10)
mientras que la multiplicación está dada por:

77. 54 CAPÍTULO 3. ESTRUCTURAS DE DATOS
Figura 3.5: Representación de un objeto autorreferido
c1 ∗ c2 = (a + bi) ∗ (c + di) = (ac − bd) + (ad + bc)i (3.11)
La división es un poco más elaborada debido a que se racionaliza el
denominador, es decir, se multiplica el numerador y el denominador
por el conjugado del denominador9
:
c1
c2
=
(a + bi)
(c + di)
=
(a + bi) ∗ (c − di)
(c + di) ∗ (c − di)
=
(ac + bd) + (bc − ad)i
c2 + d2
(3.12)
Utilice las definiciones y operaciones anteriores para abstraer un ADT
complejo, y utilı́celas para realizar una implementación de dicha enti-
dad (como se hizo para el Ejemplo 3.1).
Escriba también una clase de prueba que permita probar la imple-
mentación del ADT complejo y las respectivas operaciones aritméticas
presentadas en las Ecuaciones 3.9, 3.10, 3.11 y 3.12.
9. En base a la explicación dada en la Sección 3.4.1 y tomando como
referencia la Figura 3.5, modifique el Ejemplo 3.3 de tal forma que
sobre cargue el constructor, para que, en caso de crear un objeto sin
argumentos:
Nodo nodo = new Nodo();
se construya un objeto como el mostrado en la Figura 3.5.
Utilice cero para el atributo dato, y asegúrese de probar su constructor.
9
El conjugado de un número complejo se obtiene cambiando el signo de su componente
imaginaria, es decir: si c = a + bi es un número complejo, su conjugado está dado por
c = a − bi.

78. Capı́tulo 4
Pilas
A whole stack of memories never equal one little hope.
Charles M. Schulz
I can’t predict how reading habits will change. But I will say that
the greatest loss is the paper archive - no more a great stack of
manuscripts, letters, and notebooks from a writer’s life, but only
a tiny pile of disks, little plastic cookies where once were
calligraphic marvels.
Paul Theroux
4.1. Definición
La pila es un objeto dinámico en constante cambio.
Una pila es un conjunto ordenado de elementos en el cual se pueden
insertar y eliminar elementos únicamente por un extremo: el tope de la pila.
La caracterı́stica más importante de una pila es que el último elemento
insertado en ella es el primero en eliminarse, mientras que el primero que fue
insertado, es el último en eliminarse. Por ésta razón, se dice que una pila es
una estructura de datos de tipo LIFO (Last In First Out).
El proceso de inserción y eliminación de elementos puede observarse en
la Figura 4.1, en donde se muestra, por medio de una flecha (→), la repre-
sentación del tope de la pila. Observe cómo con cada inserción o eliminación
se modifica el tope de la pila.
La representación mostrada en la Figura 4.1, permite visualizar todos los
elementos de la pila, sin embargo, es importante señalar que en un momento
55

79. 56 CAPÍTULO 4. PILAS
Figura 4.1: Crecimiento y decrecimiento de una pila
dado, únicamente se tiene acceso al elemento que está siendo referido por el
tope de la pila, los demás elementos permanecen ocultos, tapados, por decirlo
de alguna manera, por el elemento que se encuentra en el tope de la pila.
4.1.1. Operaciones primitivas
Las operaciones primitivas o fundamentales definidas sobre una pila, son
la inserción (push) y la eliminación (pop).
1. El comportamiento definido para la operación push consiste en insertar
un nuevo elemento en la pila, mismo que constituirá el nuevo tope de
la pila.
2. El comportamiento definido para la operación pop elimina el elemento
referido por el tope de la pila, modificando en consecuencia el tope de
la pila, al elemento (si existe) que fue insertado inmediatamente antes
que el elemento eliminado.
Existen otras operaciones útiles al usar pilas, como por ejemplo, antes de
aplicar la operación pop a una pila, serı́a conveniente verificar que la pila no
esté vacı́a (operación ¿Está vacı́a?).
Otro comportamiento deseable serı́a la operación “ojeada”(peek), la cual
hecha un vistazo al elemento que se encuentra en el tope de la pila y lo regresa,
pero no lo elimina.
Las operaciones push, pop y peek, son muy comunes para la estructura de
datos pila, por lo que se conservarán dichos nombres en la implementación.

80. 4.2. IMPLEMENTACIÓN 57
Figura 4.2: Abstracción de una pila como una secuencia de nodos
4.2. Implementación
La representación de una pila, como una secuencia de nodos, se muestra en
la Figura 4.2. Los detalles de su implementación se discutirán a continuación.
4.2.1. Pila primitiva
Esta sección describe la implementación de una pila primitiva. Se ha
denominado de ésta forma, debido a que implementa una estructura de datos
que almacena un tipo de dato primitivo: int.
La definición de la clase fundamental para la implementación de la es-
tructura de datos se muestra en el Ejemplo 4.1. Los detalles de este tipo de
implementación de clases de autorreferencia se han discutido con anteriori-
dad en la Sección 3.4.1 y no se repetirán aquı́, por lo que se sugiere al lector
que la revise nuevamente, y se tome el tiempo necesario para comparar el
Ejemplo 4.1 con el Ejemplo 3.3 antes de continuar.
1 /∗ Clase que permite l a instanciacion de o b j e t o s ( nodos ) a u t o r r e f e r i d o s .
2 Cada nodo almacena un entero primitivo y una r e f e r e n c i a a
3 o b j e t o s como e l .
4 @autor Ricardo Ruiz Rodriguez
5 ∗/
6 class NodoPrimitivo {
7 private int dato ;
8 private NodoPrimitivo s i g u i e n t e ;
9
10 NodoPrimitivo ( int d) {
11 this (d , null ) ;
12 }
13
14 NodoPrimitivo ( int d , NodoPrimitivo nodo ) {
15 dato = d ;
16 s i g u i e n t e = nodo ;
17 }
18
19 public void estableceDato ( int d) {
20 dato = d ;
21 }
22

81. 58 CAPÍTULO 4. PILAS
23 public int obtenDato () {
24 return dato ;
25 }
26
27 public void e s t a b l e c e S i g u i e n t e ( NodoPrimitivo n) {
28 s i g u i e n t e = n ;
29 }
30
31 NodoPrimitivo obtenSiguiente () {
32 return s i g u i e n t e ;
33 }
34 }
Ejemplo 4.1: Definición de la clase NodoPrimitivo
La implementación de la estructura de datos pila se muestra en el Ejem-
plo 4.2, y su explicación se centrará únicamente en los métodos push, pop,
estaVacia e imprime.
1 /∗ Clase que implementa una p i l a de o b j e t o s nodo de l a c l a s e NodoPrimitivo .
2 @autor Ricardo Ruiz Rodriguez
3 ∗/
4 public class PilaPrimitiva {
5 private NodoPrimitivo tope ;
6 private String nombre ;
7
8 public PilaPrimitiva ( ) {
9 this ( ” Pila de enteros p r i m i t i v o s ” ) ;
10 }
11
12 public PilaPrimitiva ( String n) {
13 nombre = n ;
14 tope = null ;
15 }
16
17 // Metodo de insercion ( push ) de datos a l a p i l a
18 public void push ( int elemento ) {
19 i f ( estaVacia () )
20 tope = new NodoPrimitivo ( elemento ) ;
21 else
22 tope = new NodoPrimitivo ( elemento , tope ) ;
23 }
24
25 // Metodo de eliminacion ( pop ) de datos de l a p i l a
26 public int pop ( ) throws ExcepcionEDVacia{
27 i f ( estaVacia () )
28 throw new ExcepcionEDVacia ( nombre ) ;
29
30 int elemento = tope . obtenDato () ;
31 tope = tope . obtenSiguiente () ;
32
33 return elemento ;
34 }
35
36 // Metodo de v e r i f i c a c i o n de p i l a vacia ( estaVacia ?)
37 public boolean estaVacia () {

82. 4.2. IMPLEMENTACIÓN 59
38 return tope == null ;
39 }
40
41 // Metodo de impresion de l o s elementos almacenados en l a p i l a
42 public void imprime ( ) {
43 i f ( estaVacia () )
44 System . out . p r i n t f ( ”Vacia : % s n” , nombre ) ;
45 else {
46 System . out . p r i n t f ( ”La % s es : ” , nombre ) ;
47 NodoPrimitivo actual = tope ;
48
49 while ( actual != null ) {
50 //System . out . p r i n t f(” %s ” , actual . data ) ;
51 System . out . p r i n t f ( ” % s ” , actual . obtenDato ( ) ) ;
52 // actual = actual . nextNode ;
53 actual = actual . obtenSiguiente () ;
54 }
55 System . out . p r i n t l n ( ) ;
56 }
57 }
58 }
Ejemplo 4.2: Definición de la clase PilaPrimitiva
El método estaVacia (lı́neas 37-39) realiza una verificación bastante sim-
ple: si el tope de la pila es igual a null, regresa verdadero (está vacı́a), si no,
regresa falso (existe al menos un elemento).
El método push por su parte (lı́neas 18-23), recibe como argumento el
elemento a insertar en la pila (elemento), y se apoya del método estaVacia y
de los constructores para realizar la inserción:
Si la pila está vacı́a (lı́nea 19), se crea un nuevo nodo con el elemento
correspondiente (lı́nea 20) para el atributo dato, y null en su atributo
siguiente.
Si la pila no está vacı́a (lı́nea 21), se crea un nuevo nodo con el elemento
correspondiente para el atributo dato, y con el tope actual en su atri-
buto siguiente (lı́nea 22). Ası́ mismo, note que el tope es actualizado
para hacer referencia al nodo recién creado.
Ahora bien, observe que el método pop (lı́neas 26-34) posee una carac-
terı́stica particular: el método lanza (throws) una excepción ExcepcionED-
Vacia (lı́nea 26). Ésto quiere decir que, en determinadas condiciones, el méto-
do puede lanzar una excepción; para el caso del método pop, dicha condición
consiste en intentar eliminar un elemento de la pila cuando ésta está vacı́a.

83. 60 CAPÍTULO 4. PILAS
1 /∗ Ejemplo de d e f i n i c i o n de excepcion .
2 La excepcion sera lanzada cuando se haga un intento de eliminacion
3 de una estructura de datos que e s t e vacia .
4 La c l a s e RuntimeException es l a super c l a s e de l a s excepciones
5 que pueden ser lanzadas durante l a operacion normal de l a JVM.
6 @autor Ricardo Ruiz Rodriguez
7 ∗/
8 public class ExcepcionEDVacia extends RuntimeException{
9 public ExcepcionEDVacia () {
10 this ( ” Estructura de datos ” ) ;
11 }
12
13 public ExcepcionEDVacia ( String s ) {
14 super ( s + ” vacia ” ) ;
15 }
16 }
Ejemplo 4.3: Definición de la clase ExcepcionEDVacia que se utiliza para la
implementación de todas las estructuras de datos
La excepción ExcepcionEDVacia definida en el Ejemplo 4.3 es en realidad
bastante simple, ya que delega toda la responsabilidad a RuntimeException
que es la clase de la que deriva, y lo único que hace es establecer un identifi-
cador para la excepción a través de sus constructores, los cuales en realidad
utilizan el constructor de la clase padre a través de la cláusula super. Es
importante que el lector recuerde esta excepción, ya que será la excepción
que utilizarán todas las estructuras de datos que se implementan en el libro.
Continuando con el Ejemplo 4.2, el método pop verifica (lı́nea 27) si la
pila está vacı́a, si lo está, crea y lanza la excepción correspondiente (lı́nea
28); en caso contrario, recupera el dato almacenado (lı́nea 30), y desecha
el nodo correspondiente al hacer que el tope haga ahora referencia al ele-
mento siguiente del tope actual (lı́nea 31), para finalmente regresar el dato
recuperado (lı́nea 33)1
.
Por último, en el método imprime (lı́neas 42-57), si la estructura de datos
está vacı́a (lı́nea 43), se reporta (lı́nea 44); en caso contrario, se realiza un
recorrido por todos los nodos de la estructura para imprimir su contenido
(lı́neas 47-54).
La clase de prueba para la pila primitiva del Ejemplo 4.2, se presenta en
el Ejemplo 4.4. Observe cómo en la lı́nea 6 se crea la pila y se utiliza un
constructor sin argumentos.
1
En Java no hay una eliminación o liberación explı́cita de memoria, dicha labor es
delegada al recolector de basura, el cual se encarga, grosso modo, de identificar aquellos
objetos que no estén siendo referidos, para entonces liberar la memoria que utilizan.

84. 4.2. IMPLEMENTACIÓN 61
Figura 4.3: Inserción de elementos en la pila primitiva
1 /∗ Clase de prueba para PilaPrimitiva .
2 @autor Ricardo Ruiz Rodriguez
3 ∗/
4 public class PruebaPila {
5 public static void main ( String [ ] args ) {
6 PilaPrimitiva p i l a = new PilaPrimitiva ( ) ;
7
8 // Se insertan diez enteros
9 for ( int i = 0; i 10; i++){
10 p i l a . push ( i ) ;
11 p i l a . imprime () ;
12 }
13 System . out . p r i n t l n ( ) ;
14
15 try{
16 // Se intenta eliminar once enteros
17 for ( int i = 0; i 11; i++){
18 int elemento = p i l a . pop () ;
19 System . out . p r i n t f ( ”Elemento eliminado de la p i l a : % dn” ,
elemento ) ;
20 p i l a . imprime ( ) ;
21 }
22 }catch ( ExcepcionEDVacia e ) {
23 e . printStackTrace () ;
24 }
25 }
26 }
Ejemplo 4.4: Clase de prueba para la clase PilaPrimitiva
Las lı́neas 9-12 realizan la inserción en la pila de los números del cero al
nueve, y por cada inserción, se imprime todo el contenido de la pila, como se
muestra en la Figura 4.3.
Por otro lado, las lı́neas 15-24 realizan la eliminación de los elementos
de la pila. Dicho fragmento de código intenta eliminar once elementos de la

85. 62 CAPÍTULO 4. PILAS
Figura 4.4: Eliminación de elementos de la pila primitiva
pila (lı́neas 17-18)2
, y dado que el método pop puede lanzar una excepción,
el código involucrado en la eliminación debe estar dentro de una cláusula
try-catch-finally, la cual permite atrapar (cachar) las excepciones que un
método pudiera lanzar.
Si se genera un excepción ExcepcionEDVacia, ésta es atrapada y el flujo
de control se envı́a al ámbito de la cláusula catch, en donde se realiza el
correspondiente tratamiento de la excepción. Para el caso del Ejemplo 4.4,
el manejo de la excepción consiste únicamente en imprimir la secuencia de
eventos (en forma de pila) que dieron lugar a la excepción, sin embargo, es
importante aclarar que el manejo de una excepción puede ser tan elaborado
como en un momento dado se requiera.
La salida correspondiente a la eliminación de elementos de la pila primi-
tiva, se muestra en la Figura 4.4.
2
Recuerde que sólo fueron insertados diez elementos, por lo que al intentar eliminar el
décimo primero, se generará la excepción ExcepcionEDVacia.

86. 4.2. IMPLEMENTACIÓN 63
4.2.2. Pila genérica
Esta sección generaliza la implementación de una pila, de tal forma que
la estructura de datos tenga la capacidad de almacenar objetos genéricos, es
decir, objetos de cualquier clase.
Como primer paso, es preciso que el lector se tome el tiempo que considere
necesario, para comparar el Ejemplo 4.1 discutido en la sección anterior, con
el Ejemplo 4.5. Es importante resaltar que, aunque distintos, ambos ejemplos
son esencialmente equivalentes.
1 /∗ Clase que permite l a instanciacion de o b j e t o s ( nodos ) a u t o r r e f e r i d o s .
2 Cada nodo almacena un o b j e t o generico T y una r e f e r e n c i a a
3 o b j e t o s como e l .
4 @autor Ricardo Ruiz Rodriguez
5 ∗/
6 class NodoGT{
7 private T dato ;
8 private NodoGT s i g u i e n t e ;
9
10 NodoG(T d) {
11 this (d , null ) ;
12 }
13
14 NodoG(T d , NodoGT nodo ) {
15 dato = d ;
16 s i g u i e n t e = nodo ;
17 }
18
19 public void estableceDato (T d) {
20 dato = d ;
21 }
22
23 public T obtenDato () {
24 return dato ;
25 }
26
27 public void e s t a b l e c e S i g u i e n t e (NodoGT n) {
28 s i g u i e n t e = n ;
29 }
30
31 NodoGT obtenSiguiente () {
32 return s i g u i e n t e ;
33 }
34 }
Ejemplo 4.5: Definición de la clase para un nodo genérico (NodoG)
La primera diferencia que salta a la vista, además del nombre de la clase,
es la notación T . Dicha notación se utiliza en Java para especificar que la
clase gestiona objetos genéricos, es decir, que el tipo o la clase de los objetos
que almacena no está especificada en la definición de la misma, sino que se

87. 64 CAPÍTULO 4. PILAS
especifica en el momento de la instanciación del objeto3
.
La lı́nea 7 del Ejemplo 4.5 define que la clase del atributo dato es T, es
decir, un genérico, y por lo tanto, el atributo siguiente es una referencia a un
objeto que almacena objetos genéricos.
Observe cómo ahora los constructores y los métodos de tipo set, reciben
como argumentos objetos genéricos T (lı́neas 10, 14 y 19), y referencias a
objetos que a su vez almacenan objetos genéricos (lı́neas 14 y 27); mientras
que los métodos de tipo get regresan genéricos (lı́nea 23), o referencias a
objetos que almacenan objetos genéricos (lı́nea 31).
1 /∗ Clase que implementa una p i l a de o b j e t o s nodo de l a c l a s e NodoGT.
2 @autor Ricardo Ruiz Rodriguez
3 ∗/
4 public class PilaT{
5 private NodoGT tope ;
6 private String nombre ;
7
8 public Pila () {
9 this ( ” Pila generica ” ) ;
10 }
11
12 public Pila ( String n) {
13 nombre = n ;
14 tope = null ;
15 }
16
17 // Metodo de insercion ( push ) de datos a l a p i l a
18 public void push (T elemento ) {
19 i f ( estaVacia () )
20 tope = new NodoGT(elemento ) ;
21 else
22 tope = new NodoGT(elemento , tope ) ;
23 }
24
25 // Metodo de eliminacion ( pop ) de datos de l a p i l a
26 public T pop () throws ExcepcionEDVacia{
27 i f ( estaVacia () )
28 throw new ExcepcionEDVacia ( nombre ) ;
29
30 T elemento = tope . obtenDato ( ) ;
31 tope = tope . obtenSiguiente () ;
32
33 return elemento ;
34 }
35
36 // Metodo de v e r i f i c a c i o n de p i l a vacia ( estaVacia ?)
37 public boolean estaVacia () {
38 return tope == null ;
39 }
40
41 // Metodo de impresion de l o s elementos almacenados en l a p i l a
3
Observe la lı́nea 6 del Ejemplo 4.7.

88. 4.2. IMPLEMENTACIÓN 65
42 public void imprime ( ) {
43 i f ( estaVacia () )
44 System . out . p r i n t l n ( ”Vacia : ” + nombre ) ;
45 else {
46 System . out . print ( ”La ” + nombre + ” es : ” ) ;
47 NodoGT actual = tope ;
48
49 while ( actual != null ) {
50 System . out . print ( actual . obtenDato () + ” ” ) ;
51 actual = actual . obtenSiguiente () ;
52 }
53 System . out . p r i n t l n ( ) ;
54 }
55 }
56 }
Ejemplo 4.6: Definición de la clase Pila que permite almacenar objetos
genéricos
Ahora bien, las consideraciones hechas para el Ejemplo 4.5 respecto a
los genéricos, son las mismas que debe tomar en cuenta para el Ejemplo
4.6, por lo que una vez más, se pide encarecidamente al lector que compare
éste último con el Ejemplo 4.2 discutido en la sección anterior, tomando en
consideración lo explicado hasta este momento para los genéricos.
1 /∗ Clase de prueba para Pila .
2 @autor Ricardo Ruiz Rodriguez
3 ∗/
4 public class PruebaPilaGenerica {
5 public static void main ( String [ ] args ) {
6 PilaInteger p i l a = new PilaInteger () ;
7
8 // Se insertan diez enteros
9 for ( int i = 0; i 10; i++){
10 p i l a . push ( i ) ;
11 p i l a . imprime () ;
12 }
13 System . out . p r i n t l n ( ) ;
14
15 try{
16 // Se intenta eliminar once enteros
17 for ( int i = 0; i 11; i++){
18 Integer elemento = p i l a . pop () ;
19 System . out . p r i n t l n ( ”Elemento eliminado de l a p i l a : ” +
elemento ) ;
20 p i l a . imprime ( ) ;
21 }
22 }catch ( ExcepcionEDVacia e ) {
23 e . printStackTrace () ;
24 }
25 }
26 }
Ejemplo 4.7: Clase de prueba para la pila genérica

89. 66 CAPÍTULO 4. PILAS
Observe que en ninguna parte del Ejemplo 4.6 se hace explı́cita una clase
especı́fica para el genérico T, por lo que también aquı́ se hace una gestión de
genéricos en directa relación con los genéricos utilizados en el Ejemplo 4.5.
En resumen, la clase NodoG del Ejemplo 4.5 define nodos que almacenan
objetos genéricos (nodos genéricos), los cuales son utilizados de manera con-
veniente por la clase Pila del Ejemplo 4.6, para conformar una estructura de
datos dinámica que almacena objetos o nodos genéricos en forma de pila.
Finalmente, el Ejemplo 4.7 muestra la clase de prueba para la pila genérica
del Ejemplo 4.6. La lı́nea más importante del Ejemplo 4.7 es la lı́nea 6, ya que
en ella es en donde finalmente se define la clase de objetos que contendrá la
pila: Integer.
Consulte la Sección A.5.6 del Apéndice A para ampliar un poco más la
información y los detalles acerca de los genéricos en Java.
Adicionalmente, asegúrese de comprobar que la salida del Ejemplo 4.7
corresponde, en esencia, con la de la Figura 4.3 para la inserción de datos en
la pila (push), y con la de la Figura 4.4 para la eliminación (pop).
4.3. Aplicaciones
A continuación se presentan algunas de las aplicaciones más representa-
tivas de una pila, la selección presentada dista por mucho, de una selección
completa.
4.3.1. Análisis básico de expresiones
Considere la Expresión 4.1:
7 −
x × x+y
j−3
+ y
4 − 5
2
(4.1)
Se insta al lector a que sea tan amable de contestar una por una, las
siguientes preguntas:
¿Es clara? es decir ¿Se entiende?
Para valores concretos de x, y, y j ¿Podrı́a evaluarla?
¿Puede escribir la misma expresión en una sola lı́nea de texto, como lo
harı́a para un programa?

90. 4.3. APLICACIONES 67
La representación “lineal”de la Expresión 4.1 se muestra en la Expresión
4.2:
7–((x ∗ ((x + y)/(j − 3)) + y)/(4–5/2)) (4.2)
Observe que la Expresión 4.2 contiene paréntesis, los cuales son indis-
pensables para agrupar de manera apropiada las operaciones involucradas,
mientras que la representación de la Expresión 4.1 no los tiene, ya que son,
en principio, innecesarios. Ahora bien, en base a lo anterior, considere lo
siguiente:
¿Cómo saber que la Expresión 4.2 está correctamente balanceada en
cuanto a paréntesis se refiere, de tal forma que represente exactamente
lo mismo que la Expresión 4.1?
¿Y si la Expresión 4.1 fuera más grande y/o más compleja?
Considere ahora la Expresión 4.3
{x + (y − [a + b] × c) − [(d + e)]}
(h − (j − (k − [l − n])))
(4.3)
Cuya representación “lineal” está dada por la Expresión 4.4:
{x + (y–[a + b]) ∗ c–[(d + e)]}/(h–(j–(k–[l − n]))). (4.4)
Al igual que antes:
¿Cómo saber si la Expresión 4.4 está correctamente balanceada en
cuanto a sı́mbolos de agrupación se refiere? Note que ahora se han
introducido otros sı́mbolos de agrupación de expresiones (corchetes y
llaves) además de los paréntesis.
Adicionalmente ¿Cómo saber que un sı́mbolo de agrupación está cerran-
do a su correspondiente sı́mbolo de apertura?, es decir ¿Cómo saber que
los sı́mbolos de agrupación están correctamente asociados?
Deberı́a resultar claro, que es mucho más fácil para las personas compren-
der expresiones denotadas como en 4.1 o en 4.3; sin embargo, las representa-
ciones “lineales”son las que se utilizan en los lenguajes de programación, por
lo que se requiere de un mecanismo que verifique, de manera automática, que
una expresión esté bien escrita, al menos en cuanto a sı́mbolos de agrupación
se refiere, para ello, considere el siguiente pseudocódigo:

91. 68 CAPÍTULO 4. PILAS
valida = true;
p = pila vacı́a;
while(no sea fin de cadena){
procesar el siguiente sı́mbolo de la cadena;
if(sı́mbolo == ‘(’ || sı́mbolo == ‘[’ || sı́mbolo == ‘{’)
p.push(sı́mbolo);
else if(sı́mbolo == ‘)’ || sı́mbolo == ‘]’ ||
sı́mbolo == ‘}’){
if(p.estaVacia())
valida = false;
else{
Char s = p.pop();
if(s no es equivalente a sı́mbolo)
valida = false;
}
}
} // while
if(!p.estaVacia())
valida = false;
if(valida)
println(La expresión es correcta y está balanceada.);
else
println(Existe error en los sı́mbolos de agrupación.);
Algoritmo 4.1: Verificación de balanceo
Dada una expresión almacenada en una cadena, el Algoritmo 4.1 utiliza
una pila para realizar la verificación de los sı́mbolos de agrupación que se
encuentren en dicha expresión.
Se deja como ejercicio para el lector realizar una implementación de dicho
algoritmo, ası́ como la resolución de los aspectos inherentes a la equivalencia
de sı́mbolos4
.
4
Vea el Ejercicio 7.

92. 4.3. APLICACIONES 69
4.3.2. Notación interfija, postfija y prefija
Considere la suma de dos números cualesquiera A y B. Aplicar el operador
“+” a los operandos A y B, y representar la suma como A + B, tiene el
nombre de representación o notación interfija.
La notación interfija, aunque es la más común, no es la única. Existen
al menos otras dos notaciones alternativas para expresar la suma de A y B
utilizando los mismos sı́mbolos A, B y +:
1. + A B representación o notación prefija.
2. A B + representación o notación postfija.
Los prefijos “pre”, “pos” e “inter” hacen referencia a la posición relativa
del operador en relación a los operandos.
Una función en un lenguaje de programación gobernado por el paradigma
estructurado, como el lenguaje C por ejemplo, utiliza notación prefija5
, ya
que el operador suma precede a los operandos.
Conversión de interfija a postfija
Considere la Expresión 4.5:
A + B × C (4.5)
la cual implı́citamente indica:
A + (B × C) (4.6)
Suponga que se desea convertir la Expresión 4.6 a su representación en
postfija ¿Cómo proceder?
Los ejemplos siguientes asumen una representación “lineal”de las expre-
siones. En base a lo anterior, es importante que el lector tenga presente que
el proceso de conversión se basa en las reglas de precedencia de los operadores
involucrados en la expresión a convertir.
Ası́, para convertir una expresión de su notación interfija a su notación
postfija, se tienen lo siguientes pasos:
5
Considere por ejemplo la suma de dos números enviados a una función invocada me-
diante suma(a, b).

93. 70 CAPÍTULO 4. PILAS
1. A + (B × C) forma interfija.
2. A + (BC×) se convierte la multiplicación, y el nuevo elemento se con-
sidera como un solo número6
.
3. A(BC×)+ se convierte la suma con las mismas consideraciones expues-
tas en el punto anterior.
4. ABC × + se eliminan paréntesis para obtener la representación final
en postfija.
Con base en lo anterior, es posible afirmar que las dos reglas que se siguen
durante el proceso de conversión a postfija son las siguientes:
1. Las operaciones con mayor precedencia se convierten primero.
2. Después de que una parte de la expresión se ha convertido a notación
postfija, ésta se considerará como un operando único.
Ejemplo
Dada la Expresión 4.7 (note que no es la misma que la Expresión 4.6):
(A + B) × C (4.7)
convierta dicha expresión a su notación postfija.
En base a lo expuesto con anterioridad, el proceso de solución está dado
por los siguientes pasos:
1. (A + B) × C forma interfija.
2. (AB+) × C se convierte la adición.
3. (AB+)C× se convierte la multiplicación.
4. AB + C× se eliminan paréntesis: representación postfija.
6
De hecho, después de aplicar el operador, el resultado (producto) es en efecto, otro
número.

94. 4.3. APLICACIONES 71
Conversión de interfija a prefija
Las reglas para convertir una expresión de su notación interfija a su no-
tación prefija, son idénticas a las de conversión de interfija a postfija. El
único cambio a considerar, es que ahora el operador se coloca antes de los
operandos, en lugar de colocarlo después de ellos.
Aspectos a considerar
Finalmente, respecto a las notaciones prefija y postfija cabe hacer mención
de un par de consideraciones:
1. La representación prefija no siempre es una imagen reflejo de la repre-
sentación postfija.
2. El orden de los operadores en las expresiones postfijas determina el or-
den real de las operaciones al evaluar la expresión, haciendo innecesario
el uso de paréntesis.
En la sección de Ejercicios tendrá oportunidad de practicar y de ampliar
su experiencia al respecto.
4.3.3. Evaluación de expresiones
Aunque para las personas en general es más fácil y natural comprender
las expresiones interfijas7
, para el procesamiento de expresiones por medio
de una computadora no lo es.
Considere lo siguiente: dada una expresión en notación interfija con valo-
res especı́ficos ¿Cómo evaluarı́a algorı́tmicamente dicha expresión? Piense y
reflexione en ello antes de continuar.
Ahora bien, con valores especı́ficos para una expresión en notación post-
fija ¿Cómo evaluarı́a algorı́tmicamente dicha expresión? Para ésto último,
considere el siguiente algoritmo:
7
Quizá porque en su mayorı́a ası́ fuimos instruidos y ası́ estamos acostumbrados, pero
¿Qué pasarı́a si desde pequeños, en lugar de haber aprendido a realizar operaciones utili-
zando notación interfija, se nos hubiera enseñado a realizarlas utilizando notación prefija
por ejemplo? ¿Qué serı́a entonces lo fácil y natural de comprender?

95. 72 CAPÍTULO 4. PILAS
pilaOperandos = pila vacı́a;
while(no sea fin de cadena){
sı́mbolo = siguiente carácter de la cadena;
if(sı́mbolo es un operando)
pilaOperandos.push(sı́mbolo);
else{
numero2 = pilaOperandos.pop();
numero1 = pilaOperandos.pop();
resultado = numero1 sı́mbolo numero2;
pilaOperandos.push(resultado);
}
}
return pilaOperandos.pop();
Algoritmo 4.2: Evaluación de una expresión en notación postfija
La solución propuesta por el Algoritmo 4.2 se basa, como es de esperarse,
en una pila. Se deja como ejercicio al lector el análisis y comprensión de dicho
algoritmo, ası́ como su correspondiente implementación8
.
4.4. Consideraciones finales
La pila es una estructura de datos sumamente importante y ampliamente
utilizada en distintas áreas no sólo de la computación. Su definición y fun-
cionalidad es clara y simple, por lo que no es casual que haya sido la primera
estructura de datos estudiada y presentada en el libro.
Por otro lado, los conceptos expuestos en el texto para los genéricos en
Java, resultarán fundamentales para los siguientes capı́tulos, ya que todas
las estructuras de datos siguientes se basan en ellos, por lo que se invita
nuevamente al lector a realizar un repaso de los conceptos relacionados con
los genéricos, ası́ como a tener presente la importancia de los mismos a lo
largo de los capı́tulos restantes.
Adicionalmente, una vez que se han presentado los conceptos de pila
(definición y operaciones) y una propuesta de implementación, resulta fun-
8
Consulte la Sección de Ejercicios para obtener mayor información. En particular, revise
a partir del Ejercicio 8.

96. 4.4. CONSIDERACIONES FINALES 73
Figura 4.5: Diagrama de clases UML para la pila genérica
damental el conocer la relación que existe entre las clases más importantes
involucradas en la implementación de la pila genérica estudiada. El diagrama
de clases UML de la Figura 4.5 presenta dicha relación.
Insto amablemente al lector a que se tome el tiempo que considere necesa-
rio para comparar el diagrama de la Figura 4.5 con las clases que implementan
la pila genérica (Ejemplo 4.6), el nodo genérico (Ejemplo 4.5), y la excepción
de estructura de datos vacı́a (Ejemplo 4.3).
Los detalles de UML quedan fuera de los alcances del libro; sin embargo, el
diagrama de clases UML la Figura 4.5 muestra una relación de composición
entre la clase Pila y la clase NodoG de cero a muchos (0..∗), lo cual quiere
decir que una pila puede tener ninguno, o muchos nodos. Por otro lado,
también se muestra la relación de asociación uno a uno existente entre la
clase Pila y la clase ExcepcionEDVacia9
.
Asegúrese de comprender el diagrama UML de la Figura 4.5 ası́ como
su relación con los ejemplos citados, ya que en los capı́tulos siguientes, se
utilizarán este tipo de diagramas de clases UML en complemento con la
definición del ADT, para definir la implementación de la estructura de datos
correspondiente.
9
Observe que el diagrama también muestra la relación de herencia entre la clase Ex-
cepcionEDVacia y la clase RuntimeException del API de Java.

97. 74 CAPÍTULO 4. PILAS
4.5. Ejercicios
1. En el Ejemplo 4.2, el método imprime tiene las lı́neas 50 y 52 como
comentarios ¿Qué sucede si sustituye la lı́nea 51 por la lı́nea 50, y la
lı́nea 53 por la lı́nea 52? ¿Compilará? ¿Si sı́ por qué, y si no por qué?
Si compila ¿Cuál será el resultado de la ejecución?
Determine sus respuestas y después corrobore las mismas con la expe-
rimentación.
2. En el Ejemplo 4.4 se creó una pila utilizando un constructor sin ar-
gumentos. Modifique dicho ejemplo para asignar un nuevo nombre a
la pila por medio del constructor correspondiente, ası́gnele a la pila el
nombre de “Mi primera pila”, recompile y pruebe su funcionamiento.
3. En el texto, durante la explicación del Ejemplo 4.4, se menciona la
cláusula try-catch-finally, sin embargo, en dicho ejemplo sólo se mues-
tra el uso de la cláusula try-catch. Investigue y documéntese acerca
del uso y funcionamiento de la cláusula completa try-catch-finally.
También investigue más acerca del uso y manejo de excepciones, ası́ co-
mo la documentación del API respecto al método printStackTrace.
4. Modifique el Ejemplo 4.6 para que:
a) Agregue el método peek a la implementación. Recuerde que dicha
operación hecha un vistazo al elemento que se encuentra en el tope
de la pila y lo regresa, pero no lo elimina.
b) Incorpore un atributo privado numérico (n), que lleve el control
del número de elementos insertados en la pila. Al respecto no
olvide:
1) Inicializar explı́citamente dicho atributo a cero en el construc-
tor.
2) Proporcionar únicamente el método de tipo get para el atri-
buto n: obtenN().
5. Tomando como referencia el Ejemplo 4.7, modifı́quelo para que la pila
genérica del Ejemplo 4.6 almacene otro tipo de objetos además de los
de la clase Integer. Pruebe con al menos las siguientes clases:
Float.

98. 4.5. EJERCICIOS 75
String.
Persona (del Ejemplo 2.11 del Capı́tulo 2).
Cientifico (del Ejemplo 2.12 del Capı́tulo 2).
6. Utilice una pila para verificar si, dada una expresión, ésta es o no un
palı́ndromo10
.
Algunos ejemplos de palı́ndromos son:
1991
2002
Se van sus naves.
Ateo por Arabia iba raro poeta.
Dábale arroz a la zorra el abad.
Anita lava la tina.
La ruta nos aportó otro paso natural.
Las Nemocón no comen sal.
No di mi decoro, cedı́ mi don.
A la catalana banal, atácala.
Nota: Simplifı́quese la vida y no considere acentos ni la letra ñ en su
implementación.
7. Realice la implementación del Algoritmo 4.1 presentado en la Sección
4.3.1. Para lo anterior, construya una clase cuyo nombre sea Expresion,
e implemente dicho algoritmo como uno de los servicios o acciones de
la clase, identifique (nombre) al método como verificaBalance.
No olvide realizar las pruebas correspondientes para validar y verificar
la funcionalidad de su propuesta.
Sugerencia: implemente la verificación de equivalencia de sı́mbolos
como un método privado, es decir, un método que proporcione servicio
a otros métodos de la misma clase (servicio interno), pero no a los
objetos instanciados (servicios públicos).
10
Un palı́ndromo es una frase o expresión que se lee o interpreta igual procesándola de
izquierda a derecha, que de derecha a izquierda.

99. 76 CAPÍTULO 4. PILAS
8. Convierta paso a paso las siguientes expresiones en su representación
en interfija, a su correspondiente notación postfija:
a) A + B
b) A + B − C
c) (A + B) × (C − D)
d) A@B × C–D + E/F/(G + H)
e) ((A + B) × C–(D − E))@(F + G)
f ) A–B/(C × D@E)
Nota: El sı́mbolo @ representa la potencia, y es el de mayor preceden-
cia.
Solución:
a) AB+
b) AB + C−
c) AB + CD − ×
d) AB@C × D − EF/GH + /+
e) AB + C × DE − −FG + @
f ) ABCDE@ × /−
9. Convierta paso a paso las expresiones del ejercicio anterior a su repre-
sentación en notación prefija.
Solución:
a) +AB
b) − + ABC
c) × + AB − CD
d) + − ×@ABCD//EF + GH
e) @ − × + ABC − DE + FG
f ) −A/B × C@DE
10. Diseñe un algoritmo, ası́ como su correspondiente implementación, para
convertir una expresión en notación interfija en su representación:

100. 4.5. EJERCICIOS 77
a) Postfija (método obtenPostfija).
b) Prefija (método obtenPrefija).
Agregue los métodos obtenPostfija y obtenPrefija a la clase Expresion
iniciada en el Ejercicio 7. Asegúrese de probar sus implementaciones
con, al menos, los dos ejercicios anteriores.
11. Realice la implementación del Algoritmo 4.2. Implemente dicho algo-
ritmo como uno de los servicios de la clase Expresion iniciada en el
Ejercicio 7, identifique (nombre) al método como evaluaPostfija.
No olvide realizar las pruebas correspondientes para validar y verificar
la funcionalidad de su propuesta.
Sugerencia: implemente la realización de la operación representada
por sı́mbolo, como un método privado, es decir, un método que pro-
porcione servicio a otros métodos de la misma clase (servicio interno),
pero no a los objetos instanciados (servicios públicos).

101. 78 CAPÍTULO 4. PILAS

102. Capı́tulo 5
Colas de espera
An Englishman, even if he is alone, forms an orderly queue of
one.
George Mikes
5.1. Definición
Una cola de espera o simplemente cola, es un conjunto ordenado de
elementos del que se pueden eliminar dichos elementos de un extremo (llama-
do inicio de la cola), y en el que pueden insertarse elementos en el extremo
opuesto (llamado fin de la cola).
El primer elemento insertado en una cola es el primer elemento en ser
eliminado, mientras que el último elemento insertado, también es el último
en ser eliminado. Por ésta razón, se dice que una cola es una estructura de
datos de tipo FIFO (First In First Out).
En el mundo real abundan ejemplos de este tipo de estructuras:
Lı́neas aéreas.
Lı́neas de autobuses.
Colas de espera en los supermercados.
Colas de espera en los bancos.
Etcétera, etcétera, etcétera.
79

103. 80 CAPÍTULO 5. COLAS DE ESPERA
Figura 5.1: Inserción y eliminación de elementos en una cola de espera
La Figura 5.1 (a) muestra una representación de una cola de espera que
permite visualizar los elementos almacenados en la misma.
La eliminación de uno de los elementos (A) se muestra en la Figura 5.1
(b), mientras que la inserción de los elementos D y E se muestra en la Figura
5.1 (c). Observe también cómo las referencias al inicio y fin de la cola son
modificadas en cada inserción y eliminación.
5.1.1. Operaciones primitivas
Se definen tres operaciones primitivas sobre una cola de espera:
1. La operación inserta, agrega un elemento en la parte final de la cola.
También se dice que esta operación forma o enlista un elemento a la
cola.
2. La operación elimina suprime un elemento de la parte inicial de la
cola. Esta operación despacha o atiende al elemento que se encuentra
al inicio de la cola.
3. La operación estaVacia1
regresa verdadero o falso dependiendo de si
la cola de espera, contiene o no elementos respectivamente.
Una operación deseable para una cola de espera, serı́a la de imprimir los
elementos de la cola, la cual se denotará como imprime.
1
Esta operación fue definida como opcional o deseable para la pila. Para el caso de la
cola, dicha operación es ahora una primitiva, por lo que su implementación es obligatoria.

104. 5.1. DEFINICIÓN 81
Figura 5.2: Abstracción de una cola de espera como una secuencia de nodos
Figura 5.3: Diagrama de clases UML para la cola de espera
5.1.2. Representación
La representación mostrada en la Figura 5.2, es una abstracción de la
implementación que se realizará en la siguiente sección.
Observe cómo la Figura 5.2 luce muy similar a la Figura 4.2 del Capı́tulo
4. Sin embargo, la Figura 5.2 muestra el uso de dos referencias: inicio y
fin, las cuales denotan respectivamente, el primero y último de los elementos
almacenados en la cola de espera. Note que, para el caso de un solo elemento,
dichas referencias harán referencia, valga la redundancia, al mismo nodo.
Por otro lado, el diagrama de clases UML presentado en la Figura 5.3,
muestra el diseño de clases de la cola de espera que se desea implementar.
Dicho diseño complementa, en consecuencia, la definición de dicha estructura
de datos. A su vez, el diagrama de clases UML muestra también, la relación
que existe entre las clases más importantes que se involucrarán durante la
implementación de la cola de espera.
Finalmente, el diagrama de la Figura 5.3 muestra también la reutilización
de las clases NodoG y ExcepcionEDVacia, lo cual, no lo olvide, es también una
de las caracterı́sticas más importantes de la orientación a objetos. Tómese el
lector el tiempo necesario para revisar y analizar el diagrama de clases, antes
de avanzar hacia la implementación.

105. 82 CAPÍTULO 5. COLAS DE ESPERA
5.2. Implementación
El nodo genérico definido en la clase del Ejemplo 5.1 ya ha sido presentado
con anterioridad en el Capı́tulo 4 (Ejemplo 4.5) y no se explicará nuevamente.
Dicho ejemplo sólo se ha incluido aquı́ como referencia inmediata al lector,
para facilitarle la relación, y la completa comprensión de la implementación
de la cola de espera.
1 /∗ Clase que permite l a instanciacion de o b j e t o s ( nodos ) a u t o r r e f e r i d o s .
2 Cada nodo almacena un o b j e t o generico T y una r e f e r e n c i a a
3 o b j e t o s como e l .
4 @autor Ricardo Ruiz Rodriguez
5 ∗/
6 class NodoGT{
7 private T dato ;
8 private NodoGT s i g u i e n t e ;
9
10 NodoG(T d) {
11 this (d , null ) ;
12 }
13
14 NodoG(T d , NodoGT nodo ) {
15 dato = d ;
16 s i g u i e n t e = nodo ;
17 }
18
19 public void estableceDato (T d) {
20 dato = d ;
21 }
22
23 public T obtenDato () {
24 return dato ;
25 }
26
27 public void e s t a b l e c e S i g u i e n t e (NodoGT n) {
28 s i g u i e n t e = n ;
29 }
30
31 NodoGT obtenSiguiente () {
32 return s i g u i e n t e ;
33 }
34 }
Ejemplo 5.1: Nodo genérico utilizado en la cola de espera
De manera análoga, el Ejemplo 5.2 muestra la excepción utilizada por
la implementación de la cola. Dicha clase también ha sido explicada con
anterioridad en el Ejemplo 4.3.
Se invita al lector a revisar estos dos ejemplos iniciales como preámbulo
a la implementación de la cola de espera. En caso de que surgiera alguna
duda, consulte las secciones correspondientes a los ejemplos mencionados en

106. 5.2. IMPLEMENTACIÓN 83
los párrafos anteriores.
1 /∗ Ejemplo de d e f i n i c i o n de excepcion .
2 La excepcion sera lanzada cuando se haga un intento de eliminacion
3 de una estructura de datos que e s t e vacia .
4 La c l a s e RuntimeException es l a super c l a s e de l a s excepciones
5 que pueden ser lanzadas durante l a operacion normal de l a JVM.
6 @autor Ricardo Ruiz Rodriguez
7 ∗/
8 public class ExcepcionEDVacia extends RuntimeException{
9 public ExcepcionEDVacia () {
10 this ( ” Estructura de datos ” ) ;
11 }
12
13 public ExcepcionEDVacia ( String s ) {
14 super ( s + ” vacia ” ) ;
15 }
16 }
Ejemplo 5.2: Excepción utilizada en la cola de espera
La implementación de la cola de espera se muestra en el Ejemplo 5.3. An-
tes de comenzar con la explicación de los métodos que implementan las ope-
raciones primitivas, insto amablemente al lector a que compare el diagrama
de clases de la Figura 5.3, con el código del Ejemplo 5.3, ésto con la intención
de que identifique la relación que existe entre el diseño y la implementación,
representados por el diagrama de clases, y el código respectivamente.
La identificación y comprensión de atributos y constructores deberı́an
resultar totalmente claros para el lector, excepto quizá por el modificador
de nivel de acceso protected, el cual hace que el atributo correspondiente
sea accesible únicamente por las clases del mismo paquete, o por subclases
de la clase que lo define. Dicho lo anterior, la explicación del Ejemplo 5.3
iniciará con los siguientes métodos2
:
estaVacia (lı́neas 47-49) realiza una verificación bastante simple: si ini-
cio es igual a null, regresa verdadero (la cola está vacı́a), si no, regresa
falso (existe al menos un elemento).
imprime (lı́neas 52-55), si la estructura de datos está vacı́a (lı́nea 53), se
reporta (lı́nea 54); en caso contrario, se realiza un recorrido por todos
los nodos de la estructura para imprimir su contenido (lı́neas 57-62).
2
Los métodos estaVacia e imprime fueron descritos en la implementación de la pila
genérica del Ejemplo 4.6, y de hecho, son idénticos excepto por una pequeña diferencia.
Serı́a un buen ejercicio para el lector que la identificara.

107. 84 CAPÍTULO 5. COLAS DE ESPERA
1 /∗ Clase que implementa una cola de espera de o b j e t o s nodo genericos
2 de l a c l a s e NodoGT.
3 @autor Ricardo Ruiz Rodriguez
4 ∗/
5 public class ColaT{
6 protected NodoGT i n i c i o ;
7 protected NodoGT f i n ;
8 private String nombre ;
9
10 public Cola () {
11 this ( ”Cola de espera ” ) ;
12 }
13
14 public Cola ( String n) {
15 nombre = n ;
16 i n i c i o = f i n = null ;
17 }
18
19 // Metodo de insercion de datos en l a cola de espera
20 public void i n s e r t a (T elemento ) {
21 i f ( estaVacia () )
22 i n i c i o = f i n = new NodoGT(elemento ) ;
23 else {
24 // f i n = f i n . s i g u i e n t e = new NodoGT(elemento ) ;
25 f i n . e s t a b l e c e S i g u i e n t e (new NodoGT(elemento ) ) ;
26 f i n = f i n . obtenSiguiente () ;
27 }
28 }
29
30 // Metodo de eliminacion de datos de l a cola de espera
31 public T elimina ( ) throws ExcepcionEDVacia{
32 i f ( estaVacia () )
33 throw new ExcepcionEDVacia ( nombre ) ;
34
35 T elemento = i n i c i o . obtenDato () ;
36
37 // a c t u a l i z a r e f e r e n c i a s para i n i c i o y f i n
38 i f ( i n i c i o == f i n )
39 i n i c i o = f i n = null ;
40 else
41 i n i c i o = i n i c i o . obtenSiguiente () ;
42
43 return elemento ;
44 }
45
46 // Metodo de v e r i f i c a c i o n de cola de espera vacia ( estaVacia ?)
47 public boolean estaVacia () {
48 return i n i c i o == null ;
49 }
50
51 // Metodo de impresion de l o s elementos almacenados en l a cola de espera
52 public void imprime ( ) {
53 i f ( estaVacia () )
54 System . out . p r i n t l n ( ”Vacia : ” + nombre ) ;
55 else {
56 System . out . print ( ”La ” + nombre + ” es : ” ) ;

108. 5.2. IMPLEMENTACIÓN 85
57 NodoGT actual = i n i c i o ;
58
59 while ( actual != null ) {
60 System . out . print ( actual . obtenDato () + ” ” ) ;
61 actual = actual . obtenSiguiente () ;
62 }
63 System . out . p r i n t l n ( ) ;
64 }
65 }
66 }
Ejemplo 5.3: Definición de la clase Cola que permite almacenar objetos
genéricos
Los dos métodos restantes corresponden con las dos operaciones primiti-
vas que fueron definidas, y se describen a continuación:
1. El método inserta verifica, en la lı́nea 21, si la cola está vacı́a; si lo está,
se crea un nuevo nodo que contiene a elemento, y se hace que tanto
inicio como fin, hagan referencia a dicho nodo (objeto). Si la cola no
está vacı́a (lı́nea 23), se crea un nuevo nodo y se agrega al final de la
cola (lı́nea 25); adicionalmente, se establece que el último elemento es
referido por fin (lı́nea 26).
2. El método elimina verifica (lı́nea 32) si la cola está vacı́a, si lo está, crea
y lanza la excepción ExcepcionEDVacia (lı́nea 33); en caso contrario,
recupera el dato almacenado (lı́nea 35), y actualiza las referencias co-
rrespondientes para inicio y fin (lı́neas 38-41), para finalmente, regresar
el dato recuperado referido por elemento (lı́nea 43).
La clase de prueba para la cola de espera del Ejemplo 5.3, se muestra en
el Ejemplo 5.4. La lı́nea 6 define la clase (Integer) de los elementos a insertar
en la cola de espera, mientras que las lı́neas 9-12, realizan la inserción de los
números del cero al nueve. Note que por cada inserción, se imprime todo el
contenido de la cola.
Por otro lado, las lı́neas 15-24 realizan la eliminación de los elementos de
la cola. Dicho fragmento de código intenta eliminar once elementos (lı́neas
17-18)3
, y dado que el método elimina puede lanzar una excepción, el código
involucrado en la eliminación, como ya se mencionó en el Capı́tulo 4, de-
be estar dentro de una cláusula try-catch-finally, la cual permite atrapar
(cachar) las excepciones que un método pudiera lanzar.
3
Recuerde que sólo fueron insertados diez elementos, por lo que al intentar eliminar el
décimo primero, se generará la excepción ExcepcionEDVacia.

109. 86 CAPÍTULO 5. COLAS DE ESPERA
1 /∗ Clase de prueba de l a c l a s e ColaT.
2 @autor Ricardo Ruiz Rodriguez
3 ∗/
4 public class PruebaCola{
5 public static void main ( String [ ] args ) {
6 ColaInteger cola = new ColaInteger () ;
7
8 // Se insertan diez enteros
9 for ( int i = 0; i 10; i++){
10 cola . i n s e r t a ( i ) ;
11 cola . imprime () ;
12 }
13 System . out . p r i n t l n ( ) ;
14
15 try{
16 // Se intenta eliminar once enteros
17 for ( int i = 0; i 11; i++){
18 Integer elemento = cola . elimina () ;
19 System . out . p r i n t l n ( ”Elemento eliminado de l a cola : ” +
elemento ) ;
20 cola . imprime ( ) ;
21 }
22 }catch ( ExcepcionEDVacia e ) {
23 e . printStackTrace () ;
24 }
25 }
26 }
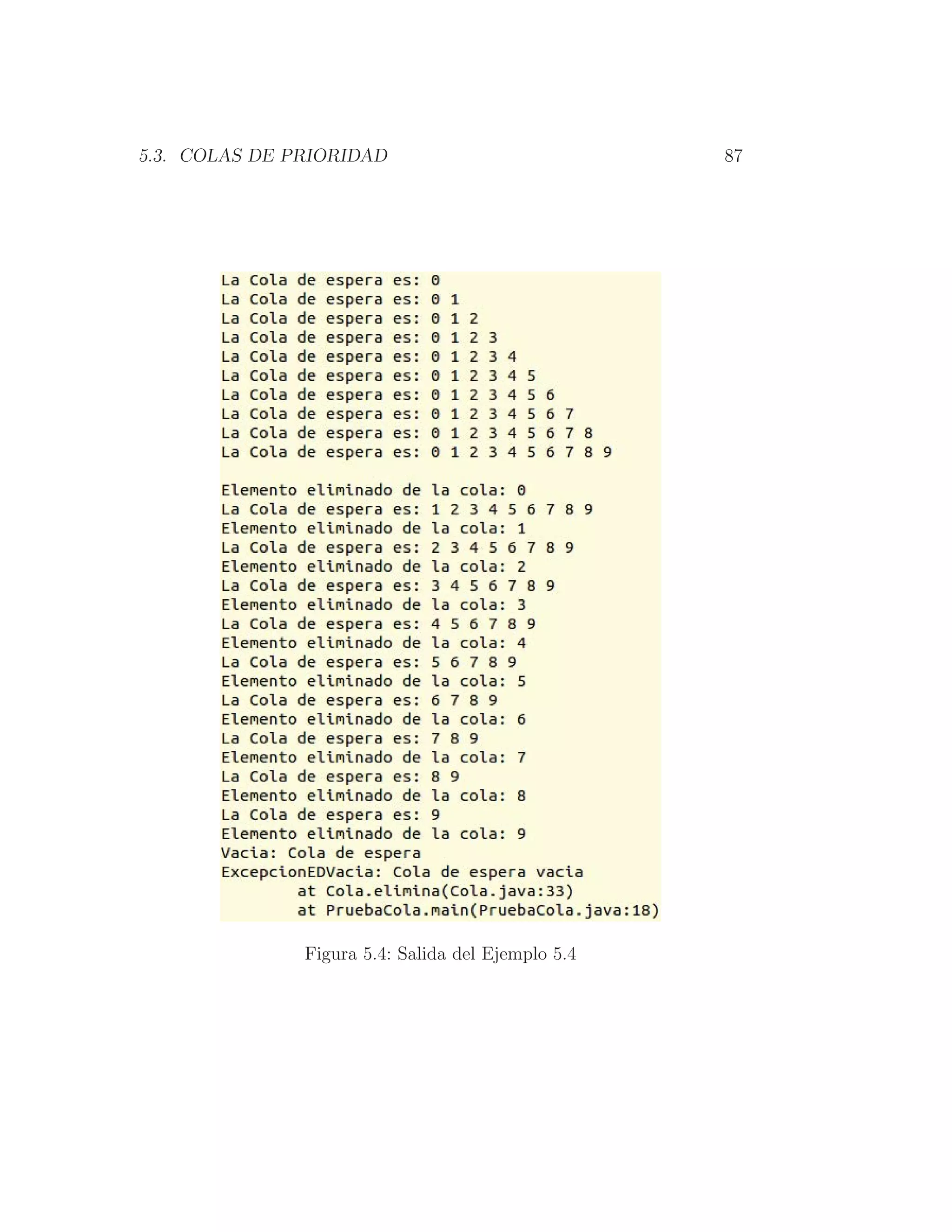
Ejemplo 5.4: Clase de prueba para la cola de espera
La salida del Ejemplo 5.4, se muestra en la Figura 5.4. Asegúrese de
comprender, antes de continuar, por qué se generan cada uno de los elementos
(renglones) que componen dicha salida.
5.3. Colas de prioridad
La cola de prioridad es una estructura de datos en la que el ordena-
miento intrı́nseco de los elementos, determina el resultado de la aplicación
de sus operaciones básicas o primitivas.
En éste sentido, existen dos tipos de colas de prioridad:
1. Cola de prioridad ascendente.
2. Cola de prioridad descendente.
Ambas estructuras de datos redefinen la forma de operación convencio-
nal respecto de una cola de espera, por lo que serán estudiadas de manera
separada.

110. 5.3. COLAS DE PRIORIDAD 87
Figura 5.4: Salida del Ejemplo 5.4

111. 88 CAPÍTULO 5. COLAS DE ESPERA
Figura 5.5: Diagrama de clases en UML para una cola de prioridad ascendente
con la redefinición del método elimina
5.3.1. Cola de prioridad ascendente
La cola de prioridad ascendente en un tipo de estructura de datos, en el
que la inserción de los elementos se realiza de manera convencional, pero la
eliminación se realiza en base al menor de los elementos almacenados en ella.
Para que ésto sea posible, los elementos que almacena la estructura de datos
deben tener una relación de orden, es decir, deben poseer algún mecanismo
que permita compararlos entre sı́.
La Figura 5.5 muestra la relación de clases en UML para una cola de
prioridad ascendente con la redefinición del método elimina. Observe cómo
se ha instrumentado la redefinición de dicho método por medio del mecanis-
mo de la herencia, y que las relaciones previamente existentes se conservan
(compare con la Figura 5.3).
Otro tipo de representación para la cola de prioridad ascendente, con-
siste en mantener ordenados los elementos de manera ascendente durante la
inserción, y conservar la operación de eliminación de la forma convencional.
Dicha representación se expresa en UML como en la Figura 5.6.
En resumen, en una cola de prioridad ascendente, los elementos se recu-
peran (eliminan) en orden ascendente respecto de la relación de orden que
guarden entre sı́. Ahora bien, para objetos con una relación de orden inheren-
te a ellos, como un objeto de la clase Integer o de la clase Float por ejemplo,
la comparación es posible, pero ¿Qué ocurre con objetos de la clase String del
API de Java, o con las clases Persona y Cientifico definidas en el Capı́tulo

112. 5.3. COLAS DE PRIORIDAD 89
Figura 5.6: Diagrama de clases en UML para una cola de prioridad ascendente
con la redefinición del método inserta
2, por mencionar sólo algunas?
Implementación
En la orientación a objetos, existe un concepto relacionado con la heren-
cia la herencia múltiple, que básicamente es la capacidad de una clase de
heredar los atributos y métodos de más de una clase padre; sin embargo,
el lenguaje de programación Java no incluye en su gramática dicha capaci-
dad, aunque por otro lado, incorpora un mecanismo que permite que una
clase se comprometa, a través de una especie de contrato, a implementar en
métodos, las operaciones definidas por medio de una interfaz (interface). La
interfaz Comparable del API de Java, obliga a las clases que la implementan,
a establecer una relación de orden entre los objetos que se deriven de ella.
Dicha relación de orden es arbitraria y está en función únicamente de las
necesidades especı́ficas de la clase en cuestión.
Para ilustrar lo anterior, considere el Ejemplo 5.5, el cual implementa una
cola de prioridad ascendente sobre escribiendo el método inserta y haciendo
uso de la interfaz Comparable, tal y como se propone en el diagrama de
clases UML de la Figura 5.6. Observe con detenimiento la lı́nea 5, la cual, en
el contexto de lo anterior, podrı́a interpretarse de la siguiente manera:
La clase ColaAscendente es una clase derivada o hija de la clase
Cola, y gestiona objetos genéricos T que definan una relación

113. 90 CAPÍTULO 5. COLAS DE ESPERA
de orden, a través de la implementación del método compareTo
definido en la interfaz Comparable.
1 /∗ Clase que implementa una cola de prioridad ascedente de o b j e t o s
2 genericos . Se r e a l i z a la sobre e s c r i t u r a del metodo i n s e r t a .
3 @autor Ricardo Ruiz Rodriguez
4 ∗/
5 public class ColaAscendenteT extends Comparable T extends ColaT{
6 public ColaAscendente ( ) {
7 this ( ”Cola de Prioridad Ascendente ” ) ;
8 }
9
10 public ColaAscendente ( String s ) {
11 super ( s ) ;
12 }
13
14 public void i n s e r t a (T elemento ) {
15 NodoGT nodoAnterior , nodoActual , nodoNuevo = new NodoGT(elemento ) ;
16
17 nodoAnterior = null ;
18 nodoActual = i n i c i o ;
19
20 while ( nodoActual != null
21 ( elemento . compareTo ( nodoActual . obtenDato ( ) ) ) 0) {
22 nodoAnterior = nodoActual ;
23 nodoActual = nodoActual . obtenSiguiente () ;
24 }
25
26 i f ( nodoAnterior == null ) { // Se i n s e r t a a l p r i n c i p i o de l a cola
27 nodoNuevo . e s t a b l e c e S i g u i e n t e ( i n i c i o ) ;
28 i n i c i o = nodoNuevo ;
29 } else { // Se i n s e r t a en medio o a l f i n a l de l a cola
30 nodoAnterior . e s t a b l e c e S i g u i e n t e ( nodoNuevo ) ;
31 nodoNuevo . e s t a b l e c e S i g u i e n t e ( nodoActual ) ;
32 i f ( nodoActual == null ) // se i n s e r t o a l f i n a l
33 f i n = nodoNuevo ;
34 }
35 }
36 }
Ejemplo 5.5: Clase que define una cola de prioridad ascendente sobre
escribiendo el método inserta
Observe que el mensaje o la invocación del método compareTo ocurre en
la lı́nea 21 del Ejemplo 5.5, y que la idea general del método inserta (lı́neas
14-35) consiste en recorrer la secuencia de nodos (lı́neas 20-24), mientras
haya nodos por procesar (lı́nea 20), y no se haya encontrado el lugar corres-
pondiente para el elemento a insertar (lı́nea 21). En éste sentido, el método
compareTo compara el objeto que recibe el mensaje con el objeto recibido
como argumento, y regresa uno de tres posibles valores4
:
4
Consulte en el API de Java la interfaz Comparable para ampliar y complementar la

114. 5.3. COLAS DE PRIORIDAD 91
1. Un entero negativo ( 0) si el objeto que recibe el mensaje, es menor
que el objeto que recibe como argumento.
2. Cero (0) si el objeto que recibe el mensaje, es igual al objeto que recibe
como argumento.
3. Un entero positivo ( 0) si el objeto que recibe el mensaje, es mayor
que el objeto que recibe como argumento.
Es importante que el lector comprenda que el método compareTo es defi-
nido en la clase que quiera establecer una relación de orden para sus objetos,
es decir, los objetos de la clase genérica T, deberán tener la definición (código)
de dicho método.
Continuando con la explicación del método inserta del Ejemplo 5.5, note
que el método ha definido objetos auxiliares (lı́neas 17 y 18), para poder rea-
lizar el ajuste de las referencias correspondientes en las lı́neas 26-33. Aquı́ ca-
be mencionar, que aunque dichos objetos pudieron haber sido definidos como
atributos de la clase ColaAscendente, en realidad no representan una carac-
terı́stica o cualidad inherente a los objetos que se deriven de dicha clase, sino
que más bien son entidades útiles para la manipulación de la estructura de
datos dentro del método, por lo que de ser atributos, aunque la implemen-
tación trabajarı́a de la misma manera, el enfoque serı́a inapropiado, esto es,
serı́a un mal diseño. El análisis y los detalles del ajuste de las referencias
de las lı́neas 22-23 y 26-33, se dejan como ejercicio para el lector, y lo ins-
to amablemente a comprender completamente su funcionamiento, antes de
continuar.
Por último, la clase de prueba para la cola de prioridad ascendente del
Ejemplo 5.5 se muestra en el Ejemplo 5.6.
Tómese el lector el tiempo que considere necesario para comparar el Ejem-
plo 5.6 con el Ejemplo 5.4, y advierta que son, esencialmente iguales.
Note que los objetos a almacenar en la cola de prioridad ascendente son
objetos de la clase Integer (lı́nea 6), por lo que, para que no haya ningún
problema en la compilación, dicha clase deberá tener la implementación
(implements) de la interfaz Comparable, y en consecuencia, la definición
del método compareTo5
.
información al respecto.
5
Se invita al lector para que realice dicha comprobación en el API de Java, antes de
compilar y ejecutar el Ejemplo 5.6.

115. 92 CAPÍTULO 5. COLAS DE ESPERA
En base a lo anterior, todos los objetos que se deseen almacenar en la co-
la de prioridad ascendente definida en el Ejemplo 5.5, deberán implementar
dicha interfaz, y definir el comportamiento requerido por el método compa-
reTo6
.
1 /∗ Clase de prueba de l a c l a s e ColaAscendenteT.
2 @autor Ricardo Ruiz Rodriguez
3 ∗/
4 public class PruebaColaAscendente {
5 public static void main ( String [ ] args ) {
6 ColaAscendenteInteger colaAscendente = new
ColaAscendenteInteger () ;
7
8 colaAscendente . i n s e r t a (1) ; colaAscendente . imprime () ;
9 colaAscendente . i n s e r t a (8) ; colaAscendente . imprime () ;
10 colaAscendente . i n s e r t a (3) ; colaAscendente . imprime () ;
11 colaAscendente . i n s e r t a (6) ; colaAscendente . imprime () ;
12 colaAscendente . i n s e r t a (5) ; colaAscendente . imprime () ;
13 colaAscendente . i n s e r t a (4) ; colaAscendente . imprime () ;
14 colaAscendente . i n s e r t a (7) ; colaAscendente . imprime () ;
15 colaAscendente . i n s e r t a (2) ; colaAscendente . imprime () ;
16 colaAscendente . i n s e r t a (9) ; colaAscendente . imprime () ;
17
18 try{
19 for ( int i = 0; i 9; i++){
20 Integer elemento = colaAscendente . elimina () ;
21 System . out . p r i n t l n ( ”Elemento eliminado de l a cola ascendente : ”
+ elemento ) ;
22 colaAscendente . imprime () ;
23 }
24 }catch ( ExcepcionEDVacia e ) {
25 e . printStackTrace () ;
26 }
27 }
28 }
Ejemplo 5.6: Clase de prueba para la cola de prioridad ascendente
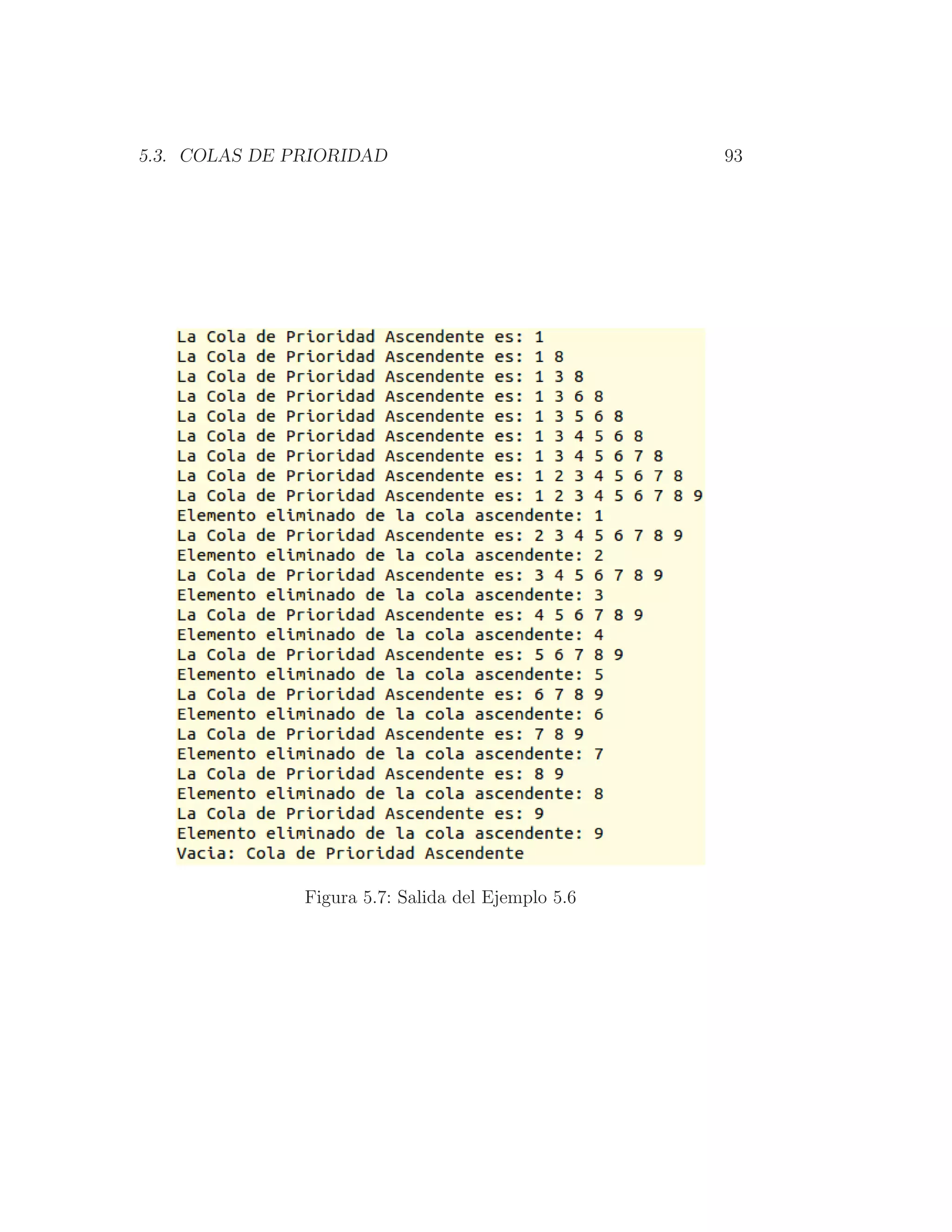
Por último, observe que a diferencia del Ejemplo 5.4, el Ejemplo 5.6 in-
serta intencionalmente nueve números de manera desordenada, ya que la
implementación de cola de prioridad propuesta (Ejemplo 5.5) los mantie-
ne ordenados dentro de la estructura de datos, mientras que la eliminación
(lı́neas 18-26) se realiza de manera convencional. La salida del Ejemplo 5.6
se muestra en la Figura 5.7.
6
No olvide ésto el lector, ya que será de suma importancia para la realización de algunos
de los ejercicios del capı́tulo.

116. 5.3. COLAS DE PRIORIDAD 93
Figura 5.7: Salida del Ejemplo 5.6

117. 94 CAPÍTULO 5. COLAS DE ESPERA
Figura 5.8: Diagrama de clases en UML para una cola de prioridad ascendente
con la redefinición del método elimina
5.3.2. Cola de prioridad descendente
La cola de prioridad descendente, es análoga en lo general a la cola de
prioridad ascendente.
La cola de prioridad descendente es un tipo de estructura de datos en
el que la inserción de los elementos se realiza también de la manera con-
vencional, pero la eliminación se realiza en base al mayor de los elementos
almacenados en ella. Al igual que para su contra parte, para que ésto último
sea posible, es necesario que los elementos que almacena la estructura de
datos tengan una relación de orden, es decir, es preciso que incorporen algún
mecanismo que les permita compararlos entre sı́.
La Figura 5.8 muestra la relación de clases en UML para una cola de
prioridad descendente con la redefinición del método elimina. Una vez más,
note cómo se ha instrumentado la redefinición de dicho método por medio
del mecanismo de la herencia, y que las relaciones (compare con la Figura
5.3) previamente existentes se conservan.
Al igual que para la cola de prioridad ascendente, otro tipo de represen-
tación para la cola de prioridad descendente consiste en mantener ordenados
los elementos de manera descendente durante la inserción, y conservar la
operación de eliminación de la forma convencional, tal y como se muestra en
la representación del diagrama de clases UML de la Figura 5.9.
Por último, recuerde que en una cola de prioridad descendente los ele-
mentos se recuperan (eliminan) en orden descendente, respecto de la relación

118. 5.4. CONSIDERACIONES FINALES 95
Figura 5.9: Diagrama de clases en UML para una cola de prioridad ascendente
con la redefinición del método inserta
de orden que guardan entre sı́. Los detalles de la implementación, se dejan
como ejercicio para el lector.
5.4. Consideraciones finales
Las colas de espera, y las colas de prioridad ascendentes y descendentes,
tienen amplias y muy variadas aplicaciones, que van desde la simulación y
modelado de situaciones relacionadas con las lı́neas de espera que hacemos
todos los dı́as (bancos, boletos, casetas de cobro, etc.), hasta aspectos de
bajo nivel relacionado con el funcionamiento de los sistemas operativos por
ejemplo.
Las colas de prioridad son un ejemplo sumamente claro en el que la defini-
ción de la estructura de datos o ADT, es independiente de la implementación.
En este capı́tulo, se propusieron y presentaron dos posibles implementaciones
para cada uno de los dos tipos de colas de prioridad, y se realizó la imple-
mentación completa de una de ellas, las implementaciones restantes se dejan
como ejercicio para el lector.
Finalmente, la introducción hacia las relaciones de orden en los objetos
por medio de la interfaz Comparable, resultará fundamental para los capı́tu-
los siguientes, por lo que se invita al lector a estudiar detenidamente estos
conceptos, y complementarlos con información adicional como ejercicio y la-
bor de investigación. Ası́ mismo, resulta sumamente importante que el lector

119. 96 CAPÍTULO 5. COLAS DE ESPERA
realice la selección de ejercicios propuestos al final del capı́tulo, los cuales
tienen, como todos los ejercicios del libro, la finalidad de reforzar, ampliar, y
poner en práctica sus conocimientos. Le auguro éxito.

120. 5.5. EJERCICIOS 97
5.5. Ejercicios
1. En el Ejemplo 5.3, el método inserta tiene la lı́nea 24 como comentario
¿Qué sucede si sustituye la lı́nea 25 por la lı́nea 24? ¿Compilará? Si
sı́ ¿por qué?, y si no ¿Por qué? Si compila ¿Cuál será el resultado de la
ejecución?
Determine sus respuestas, y después corrobore las mismas con la expe-
rimentación.
2. En el Ejemplo 5.4 se creó una cola de espera utilizando un constructor
sin argumentos. Modifique dicho ejemplo para asignar un nuevo nombre
a la cola por medio del constructor correspondiente, ası́gnele el nombre
de “Mi primera cola de espera”, recompile, y pruebe su funcionamiento.
3. Modifique el Ejemplo 5.3 para que:
a) Agregue el método peek a la implementación. Dicha operación
funciona de la siguiente manera: hecha un vistazo al elemento que
se encuentra en el inicio de la cola de espera y lo regresa, pero no
lo elimina.
b) Incorpore un atributo privado numérico (n), que lleve el control del
número de elementos insertados en la cola de espera. Al respecto
no olvide:
1) Inicializar explı́citamente dicho atributo a cero en el construc-
tor.
2) Proporcionar únicamente el método de tipo get para el atri-
buto n: obtenN().
4. Tomando como referencia el Ejemplo 5.4, modifı́quelo para que la cola
de espera del Ejemplo 5.3 almacene otro tipo de objetos además de los
de la clase Integer. Pruebe con al menos las siguientes clases:
Float.
String.
Persona (del Ejemplo 2.11 del Capı́tulo 2).
Cientifico (del Ejemplo 2.12 del Capı́tulo 2).

121. 98 CAPÍTULO 5. COLAS DE ESPERA
(a) Estado inicial
(b) Estado siguiente
Figura 5.10: Abstracción y representación de Round robin
5. Utilizando una cola de espera como la del Ejemplo 5.3, implemente el
algoritmo de Round robin.
Round robin es un método para seleccionar todos los elementos en un
grupo de manera equitativa y en orden, se comienza con el primer
elemento de la cola de espera y se procesa, y se continua de manera
progresiva hasta llegar al último elemento de la cola, para empezar
nuevamente desde el primer elemento. El principio general subyacente
detrás del método, consiste en que cada persona toma una parte de un
elemento compartido en cantidades iguales.
Considere la Figura 5.10 (a), la cual representa el estado inicial de una
cola de espera de números enteros que representan las cantidades a
considerar (quantum). El estado siguiente (Figura 5.10 (b)) consiste en
atender (restarle uno al quantum) al nodo que se encuentra al inicio de
la cola, y volverlo a formar al final de la misma para atender de manera
análoga a los siguientes nodos. Tome en consideración que, una vez que
el número llega a cero, el nodo correspondientes es eliminado.
El proceso anteriormente descrito continúa hasta atender o despachar
a todos los nodos formados en la cola. Para ello:
a) Genere un número aleatorio entre 10 y 50, el cual representará el
número de nodos que contendrá la cola de espera.

122. 5.5. EJERCICIOS 99
b) Por cada nodo, genere nuevamente un número aleatorio entre 1 y
500, mismo que representará el quantum asignado a cada nodo.
No olvide construir también una clase de prueba para su implementa-
ción. La salida de su programa puede ser en la salida estándar o en un
archivo de texto. Es importante que compruebe el adecuado funciona-
miento de su implementación, ya que se reutilizará en otros ejercicios
del libro.
6. Modifique el Ejemplo 5.6 para que la cola de prioridad ascendente del
Ejemplo 5.5, almacene otro tipo de objetos además de los de la clase
Integer. Pruebe con al menos las siguientes clases:
Float.
String.
Persona (del Ejemplo 2.11 del Capı́tulo 2).
Cientifico (del Ejemplo 2.12 del Capı́tulo 2).
Tome en cuenta que las clases Float y String del API de Java imple-
mentan la interfaz Comparable, pero que las clases Persona y Cientifico
no, por lo que como primer paso, deberá hacer que dichas clases imple-
menten la interfaz Comparable, y definan el método compareTo. Para
ello:
a) Realice el ordenamiento en base al atributo que representa la edad
de la persona para las instancias de la clase Persona.
b) Realice el ordenamiento en base al atributo que representa la es-
pecialidad del cientı́fico para las instancias de la clase Cientifico.
Como guı́a adicional para el lector, la clase PersonaComparable del
Ejemplo 5.7 realiza la implementación de la interfaz Comparable.
Observe cómo dicho ejemplo es esencialmente igual al Ejemplo 2.11
del Capı́tulo 2. Compare ambos ejemplos, estúdielos, ponga especial
atención en las lı́neas 5 y 57-63 del Ejemplo 5.7, y termine de resolver
lo que se planteó en este ejercicio.
1 /∗ La c l a s e PersonaComparable implementa l a i n t e r f a z Comparable
2 y define e l metodo compareTo .
3 @autor Ricardo Ruiz Rodriguez
4 ∗/

123. 100 CAPÍTULO 5. COLAS DE ESPERA
5 public class PersonaComparable implements
ComparablePersonaComparable{
6 private String nombre ;
7 private int edad ;
8 private String nacionalidad ;
9
10 PersonaComparable ( String n) {
11 nombre = n ;
12 }
13
14 PersonaComparable ( String n , int e ) {
15 nombre = n ;
16 edad = e ;
17 }
18
19 PersonaComparable ( String n , int e , String nac ) {
20 nombre = n ;
21 edad = e ;
22 nacionalidad = nac ;
23 }
24
25 public void estableceNombre ( String n) {
26 nombre = n ;
27 }
28
29 public String obtenNombre () {
30 return nombre ;
31 }
32
33 public void estableceEdad ( int e ) {
34 edad = e ;
35 }
36
37 public int obtenEdad () {
38 return edad ;
39 }
40
41 public void estableceNacionalidad ( String n) {
42 nacionalidad = n ;
43 }
44
45 public String obtenNacionalidad ( ) {
46 return nacionalidad ;
47 }
48
49 public void mensaje ( ) {
50 System . out . p r i n t l n ( ”Puedo hablar , mi nombre es ” +
obtenNombre () ) ;
51 }
52
53 public void comer ( ) {
54 System . out . p r i n t l n ( ”M
m
m
m
m
m uno de l o s p l a c e r e s de la vida . . . ” ) ;
55 }
56
57 public int compareTo ( PersonaComparable p) {
58 i f ( edad p . obtenEdad () )
59 return −1;

124. 5.5. EJERCICIOS 101
60 else i f ( edad p . obtenEdad () )
61 return 1 ;
62 return 0 ;
63 }
64 }
Ejemplo 5.7: Clase que implementa la interfaz Comparable
7. En base a las consideraciones hechas en el texto respecto de la cola de
prioridad ascendente, y al diseño propuesto por el diagrama de clases
UML de la Figura 5.5, realice la implementación de la cola de prioridad
ascendente correspondiente, y pruébela con las clases y las considera-
ciones hechas en el Ejercicio 6.
8. Realice la implementación de una cola de prioridad descendente de
manera análoga a la de su contraparte del Ejemplo 5.5. Para lo anterior,
tome en cuenta las consideraciones hechas en el texto, y lo expuesto en
el diseño representado por el diagrama de clases UML de la Figura 5.9.
No olvide definir también la clase de prueba correspondiente para su
propuesta. Puede basarse en la del Ejemplo 5.6.
Para sus pruebas, tome en cuenta al menos, las clases y consideraciones
propuestas en el Ejercicio 6.
9. En base a las consideraciones hechas en el texto respecto de la cola
de prioridad descendente, y al diseño propuesto por el diagrama de
clases UML de la Figura 5.8, realice la implementación de la cola de
prioridad descendente correspondiente, y pruébela con las clases y las
consideraciones hechas en el Ejercicio 6.
10. Considere la abstracción de la estructura de datos compuesta mostrada
en la Figura 5.11.
La estructura de datos de la Figura 5.11, está compuesta por una cola
de espera y varias pilas, una por cada nodo formado en la cola. Note
que cada nodo de la cola de espera, conserva una referencia a objetos
como él, y una referencia a objetos de tipo pila.
Este ejercicio consiste en hacer una representación de una fila de su-
permercado, en donde cada nodo formado en la cola de espera, simula
un carrito de supermercado con diferentes productos almacenados en

125. 102 CAPÍTULO 5. COLAS DE ESPERA
Figura 5.11: Abstracción de una estructura de datos compuesta
él en forma de pila7
. Cada nodo de la pila representa un producto, por
lo que se requiere que la información que almacena la pila sean cade-
nas que representan la descripción del producto: leche, jamón, huevos,
cacahuates, etc.
Escriba un programa que modele e implemente la estructura de datos
planteada por el diagrama de la Figura 5.11. Serı́a sumamente con-
veniente y recomendable para el lector que, como parte de su diseño,
realizara el diagrama de clases UML de su propuesta de solución.
7
En la vida real no necesariamente es ası́, pero para el caso del ejercicio propuesto,
considérela de esa manera.

126. Capı́tulo 6
Listas enlazadas
I’m very much into making lists and breaking things apart into
categories.
David Byrne
Lists have always implied social order.
David Viscott
6.1. Definición
Una lista es, en general, una colección lineal de elementos, mientras que
una lista enlazada es, en el contexto que nos compete, una colección lineal
de objetos (nodos) auto referidos.
Se tiene acceso a una lista enlazada por medio de una referencia al primer
nodo de la lista. Aunque resulta más conveniente, por las caracterı́sticas
inherentes a la estructura de datos, que existan dos referencias a la misma:
una que refiera el inicio de la lista, y otra que refiera el fin de la lista. El
acceso a los nodos intermedios subsecuentes, se realiza a través del enlace o
referencia que contiene cada uno de ellos.
Una lista enlazada es más conveniente que un arreglo estático por ejemplo,
cuando no es posible determinar con anticipación el número de elementos a
almacenar en la estructura de datos.
Las listas enlazadas son dinámicas, por lo que se puede aumentar o dismi-
nuir a discreción el número de elementos de una lista. Un aspecto importante
a considerar respecto a las listas enlazadas, es que pueden, por conveniencia,
103

127. 104 CAPÍTULO 6. LISTAS ENLAZADAS
mantenerse en orden1
insertando cada nuevo elemento en el punto apropiado
dentro de la lista enlazada.
Normalmente, los nodos de las listas enlazadas no están almacenados en
forma contigua en la memoria; sin embargo, lógicamente los nodos aparecen
como contiguos. Ésto obedece a su representación fı́sica y lógica respectiva-
mente.
6.1.1. Operaciones primitivas
Se definen cinco operaciones primitivas sobre una lista enlazada:
1. La operación insertaAlInicio, agrega un elemento al inicio de la lista
enlazada.
2. La operación insertaAlFinal, agrega un elemento al final de la lista
enlazada.
3. La operación eliminaDelInicio elimina un elemento del inicio de la
lista enlazada.
4. La operación eliminaDelFinal elimina un elemento del final de la lista
enlazada.
5. La operación estaVacia regresa verdadero o falso, dependiendo de si
la lista enlazada contiene o no elementos respectivamente.
Tome en cuenta que los elementos de una lista enlazada podrı́an ser inser-
tados en cualquier parte, y que en función de ellos, podrı́an ser definidas más
operaciones sobre una lista enlazada, por lo que el mecanismo de inserción es-
tará en función directa de las necesidades especı́ficas para la implementación
de la estructura de datos.
En éste sentido, si se desea mantener una lista enlazada ordenada por
ejemplo, se deberá ir recorriendo la lista enlazada de manera secuencial, hasta
encontrar el lugar apropiado para la inserción de cada uno de los elementos
que la conforman.
Por otro lado, la eliminación de un elemento particular, podrı́a consistir en
primer lugar, en la localización de dicho elemento dentro de la lista enlazada.
1
Puede resultar sumamente conveniente, pero en definitiva, no es una caracterı́stica
inherente a la estructura de datos.

128. 6.1. DEFINICIÓN 105
Figura 6.1: Abstracción de una lista enlazada como una secuencia de nodos
Si existe, se procede a su eliminación; en caso contrario, se deberı́a indicar que
el elemento que se está intentando eliminar, no existe dentro de la estructura
de datos.
6.1.2. Representación
Como se mencionó en el apartado anterior, el acceso a una lista enlazada
se realiza por al menos una referencia al primer nodo de dicha lista enlazada.
Aunque por otro lado, resulta más conveniente, por las caracterı́sticas inhe-
rentes a la estructura de datos, que existan dos referencias hacia la misma:
una que refiera el inicio de la lista enlazada, y otra que refiera el fin de la
lista enlazada.
El acceso a los nodos intermedios subsecuentes, se realiza a través del
enlace o referencia que contiene cada uno de ellos. Por regla convencional,
para marcar el fin de la lista enlazada, el enlace al siguiente nodo, en el último
nodo de la lista enlazada, se establece a null.
La representación mostrada en la Figura 6.1, es una abstracción de la
implementación que se realizará en la siguiente sección, y coincide con la
representación lógica de una lista enlazada.
Observe cómo la Figura 6.1 luce muy similar a la Figura 5.2 del Capı́tulo
5, ya que hace uso también de dos referencias: inicio y fin, las cuales denotan
respectivamente, el primero y el último de los elementos almacenados en la
lista enlazada. Note también que, para el caso de un solo elemento, dichas
referencias harán referencia, valga la redundancia, al mismo nodo.
Por otro lado, el diagrama de clases UML presentado en la Figura 6.2,
muestra el diseño de clases de la lista enlazada que se desea implementar.
Dicho diseño complementa, en conjunción con la definición hecha con ante-
rioridad, el concepto de lista enlazada.
A su vez, el diagrama de clases UML de la Figura 6.2, muestra también
la relación que existe entre las clases más importantes que se involucrarán

129. 106 CAPÍTULO 6. LISTAS ENLAZADAS
Figura 6.2: Diagrama de clases UML para la lista enlazada
durante la implementación de la lista enlazada. Tome el lector el tiempo que
considere necesario para revisar, analizar y comprender el diagrama de clases
de la Figura 6.2, antes de avanzar a la siguiente sección.
6.2. Implementación
La implementación de una lista enlazada se muestra en el Ejemplo 6.1.
Note que en base a lo descrito en el diagrama de clases UML de la Figura 6.2,
y a lo definido en el código fuente de dicho ejemplo, se hace uso de las clases
NodoG y ExcepcionEDVacia, mismas que han sido explicadas y analizadas
en capı́tulos anteriores, por lo que ya no se presentan ni se discuten aquı́2
.
Adicionalmente a lo anterior, el Ejemplo 6.1 muestra la definición de
los métodos estaVacia e imprime, los cuales también han sido presentados
en ejemplos anteriores; de hecho, se han reutilizado con toda la intención, ya
que el comportamiento representado por ellos, cumple con los requerimientos
necesarios para una lista enlazada. En base a lo anterior, únicamente se
describirán los siguientes métodos:
insertaAlInicio (lı́neas 18-23), como su nombre lo indica, el método inserta
elementos en la parte referida por inicio.
Si la estructura de datos está vacı́a (lı́nea 19), se crea el nodo (objeto)
con el elemento correspondiente, el cual será referido tanto por ini-
cio como por fin (lı́nea 20). En caso contrario, se inserta el elemento
siguiendo la misma idea que se utilizó para la pila (lı́nea 22).
2
Si el lector quiere mayor referencia de dichas clases, refiérase a los Capı́tulos 4 y 5.

130. 6.2. IMPLEMENTACIÓN 107
insertaAlFinal (lı́neas 25-32), como su nombre lo indica, el método inserta
elementos en la parte referida por fin.
Si la estructura de datos está vacı́a (lı́nea 26), se crea el nodo (objeto)
con el elemento correspondiente, el cual será referido tanto por ini-
cio como por fin (lı́nea 27)3
. En caso contrario, se inserta el elemento
siguiendo la misma idea que se utilizó para la cola de espera (lı́neas
29-30).
1 /∗ Clase que implementa una l i s t a enlazada de o b j e t o s genericos de l a
c l a s e NodoGT.
2 @autor Ricardo Ruiz Rodriguez
3 ∗/
4 public class Lista T{
5 private NodoGT i n i c i o ;
6 private NodoGT f i n ;
7 private String nombre ;
8
9 public Lista () {
10 this ( ” Lista ” ) ;
11 }
12
13 public Lista ( String n) {
14 nombre = n ;
15 i n i c i o = f i n = null ;
16 }
17
18 public void i n s e r t a A l I n i c i o (T elemento ) {
19 i f ( estaVacia () )
20 i n i c i o = f i n = new NodoGT(elemento ) ;
21 else
22 i n i c i o = new NodoGT(elemento , i n i c i o ) ;
23 }
24
25 public void i n s e r t a A l F i n a l (T elemento ) {
26 i f ( estaVacia () )
27 i n i c i o = f i n = new NodoGT(elemento ) ;
28 else {
29 f i n . e s t a b l e c e S i g u i e n t e (new NodoGT(elemento ) ) ;
30 f i n = f i n . obtenSiguiente () ;
31 }
32 }
33
34 public T e l i m i n a D e l I n i c i o () throws ExcepcionEDVacia{
35 i f ( estaVacia () )
36 throw new ExcepcionEDVacia ( nombre ) ;
37
38 T elemento = i n i c i o . obtenDato () ;
39
40 // a c t u a l i z a r e f e r e n c i a s
41 i f ( i n i c i o == f i n )
3
Observe que hasta aquı́, se hace exactamente lo mismo que para el método anterior:
insertaAlInicio.

131. 108 CAPÍTULO 6. LISTAS ENLAZADAS
42 i n i c i o = f i n = null ;
43 else
44 i n i c i o = i n i c i o . obtenSiguiente () ;
45
46 return elemento ;
47 }
48
49 public T eliminaDelFinal ( ) throws ExcepcionEDVacia{
50 i f ( estaVacia () )
51 throw new ExcepcionEDVacia ( nombre ) ;
52
53 T elemento = f i n . obtenDato () ;
54
55 // a c t u a l i z a r e f e r e n c i a s
56 i f ( i n i c i o == f i n )
57 i n i c i o = f i n = null ;
58 else { // determina quien sera e l nuevo f i n (Por que ?)
59 NodoGT actual = i n i c i o ;
60 while ( actual . obtenSiguiente () != f i n )
61 actual = actual . obtenSiguiente ( ) ;
62
63 f i n = actual ; // nodo actual es e l nuevo f i n
64 actual . e s t a b l e c e S i g u i e n t e ( null ) ;
65 }
66
67 return elemento ;
68 }
69
70 public boolean estaVacia () {
71 return i n i c i o == null ;
72 }
73
74 public void imprime ( ) {
75 i f ( estaVacia () )
76 System . out . p r i n t l n ( ”Vacia : ” + nombre ) ;
77 else {
78 System . out . print ( ”La ” + nombre + ” es : ” ) ;
79 NodoGT actual = i n i c i o ;
80
81 while ( actual != null ) {
82 System . out . print ( actual . obtenDato () + ” ” ) ;
83 actual = actual . obtenSiguiente ( ) ;
84 }
85 System . out . p r i n t l n ( ) ;
86 }
87 }
88 }
Ejemplo 6.1: Definición de la clase Lista que permite almacenar objetos
genéricos
eliminaDelInicio (lı́neas 34-47), como su nombre lo indica, este método
elimina elementos en la parte referida por inicio.
Si la estructura de datos está vacı́a (lı́nea 35), se lanza la excepción

132. 6.2. IMPLEMENTACIÓN 109
ExcepcionEDVacia (lı́nea 36). En caso contrario, se procede a la elimi-
nación del elemento de manera análoga a como se hizo para la cola de
espera (lı́neas 38-46).
eliminaDelFinal (lı́neas 49-68), como su nombre lo indica, elimina elemen-
tos en la parte referida por fin.
Si la estructura de datos está vacı́a (lı́nea 50), se lanza la excepción
ExcepcionEDVacia (lı́nea 51). En caso contrario, se procede a la elimi-
nación del elemento correspondiente, para ello:
1. Si sólo existe un elemento (lı́nea 56), se actualizan las referencias
(lı́nea 57). En caso contrario (lı́nea 58):
2. Se realiza un recorrido (lı́neas 59-61) por la estructura de datos
desde el inicio (lı́nea 59), para determinar el elemento anterior al
referido por fin (¿Por qué?).
3. Se actualizan las referencias correspondientes (lı́neas 63-64).
La clase de prueba para el Ejemplo 6.1 se muestra en el Ejemplo 6.2. Note
que se insertan diez números enteros, y que para los números pares se utiliza
el método insertaAlInicio, mientras que para los números impares se utiliza
el método insertaAlFinal. Observe también cómo para la eliminación ocurre,
de manera análoga, lo correspondiente.
1 /∗ Clase de prueba para l a c l a s e Lista .
2 @autor Ricardo Ruiz Rodriguez
3 ∗/
4 public class PruebaLista {
5 public static void main ( String [ ] args ) {
6 Lista Integer l i s t a = new Lista Integer () ;
7
8 for ( int i = 0; i 10; i++){
9 i f ( i % 2 == 0)
10 l i s t a . i n s e r t a A l I n i c i o ( i ) ; // par
11 else
12 l i s t a . i n s e r t a A l F i n a l ( i ) ; // impar
13 l i s t a . imprime ( ) ;
14 }
15 System . out . p r i n t l n ( ) ;
16
17 try{
18 for ( int i = 0; i 10; i++){
19 Integer elemento ;
20 i f ( i % 2 == 0)
21 elemento = l i s t a . e l i m i n a D e l I n i c i o ( ) ; // impar
22 else
23 elemento = l i s t a . eliminaDelFinal () ; // par

133. 110 CAPÍTULO 6. LISTAS ENLAZADAS
24 System . out . p r i n t l n ( ”Elemento eliminado de l a l i s t a : ” +
elemento ) ;
25 l i s t a . imprime () ;
26 }
27 }catch ( ExcepcionEDVacia e ) {
28 e . printStackTrace () ;
29 }
30 }
31 }
Ejemplo 6.2: Clase de prueba para la clase Lista
Finalmente, la Figura 6.3 muestra la salida del Ejemplo 6.2.
6.3. Herencia vs. composición
Uno de los aspectos más importantes de la programación orientada a
objetos, es la conveniencia de la reutilización de código por medio de la
abstracción. En éste sentido, dos de los esquemas más comunes al respecto
son: la herencia y la composición.
Esta sección presenta por medio de un ejemplo ya conocido y presenta-
do previamente al lector, la implementación de una pila utilizando una lista
enlazada. Dicha implementación se realiza empleando los dos enfoques men-
cionados con anterioridad. Ası́ mismo, se analizan las ventajas y desventajas
de cada uno de ellos.
6.3.1. Implementación de una pila utilizando herencia
La implementación de una pila, por medio de una lista con un enfoque
basado en la herencia, es en realidad bastante simple, tal y como lo muestra
el código del Ejemplo 6.3.
Observe que la clase del Ejemplo 6.3 no define atributos, y que únicamente
define dos constructores y los métodos push y pop; lo cual también ha sido
representado en el diagrama de clases UML de la Figura 6.4.
Insto nueva y amablemente al lector a que compare, contraste, y analice
con detenimiento, antes de continuar, a la Figura 6.4 con el Ejemplo 6.3.
Note que los métodos push (lı́neas 14-16), y pop (lı́neas 18-20) del Ejemplo
6.3, no hacen otra cosa más que encapsular el comportamiento de los métodos
insertaAlInicio y eliminaDelInicio respectivamente, los cuales son servicios
definidos en la clase Lista del Ejemplo 6.1, y es posible accederlos, debido a
que la clase PilaH hereda de la clase Lista (lı́nea 5).

134. 6.3. HERENCIA VS. COMPOSICIÓN 111
Figura 6.3: Salida del Ejemplo 5.4

135. 112 CAPÍTULO 6. LISTAS ENLAZADAS
Figura 6.4: Diagrama de clases UML para la implementación de una pila
utilizando herencia y una lista lista enlazada
Observe que como parte del mecanismo de la herencia, tampoco es nece-
sario definir el comportamiento de los métodos estaVacia e imprime dentro
de la clase PilaH, ya que se encuentran definidos en la clase Lista.
1 /∗ Clase que implementa una p i l a de o b j e t o s nodo de l a c l a s e NodoGT,
2 u t i l i z a n d o herencia y una l i s t a enlazada .
3 @autor Ricardo Ruiz Rodriguez
4 ∗/
5 public class PilaHT extends Lista T{
6 public PilaH ( ) {
7 this ( ” Pila generica ” ) ;
8 }
9
10 public PilaH ( String n) {
11 super (n) ;
12 }
13
14 public void push (T elemento ) {
15 i n s e r t a A l I n i c i o ( elemento ) ;
16 }
17
18 public T pop () throws ExcepcionEDVacia{
19 return e l i m i n a D e l I n i c i o ( ) ;
20 }
21 }
Ejemplo 6.3: Definición de la clase PilaH que implementa una pila de objetos
genéricos utilizando herencia y una lista enlazada
El primero de dichos comportamientos forma parte de la definición de las

136. 6.3. HERENCIA VS. COMPOSICIÓN 113
primitivas de la estructura de datos pila, mientras que el segundo es utilizado
en la clase PruebaPilaH del Ejemplo 6.4 (lı́neas 11 y 20), la cual es la clase
de prueba del Ejemplo 6.3.
1 /∗ Clase de prueba para PilaH .
2 @autor Ricardo Ruiz Rodriguez
3 ∗/
4 public class PruebaPilaH{
5 public static void main ( String [ ] args ) {
6 PilaHInteger p i l a = new PilaHInteger () ;
7
8 // Se insertan diez enteros
9 for ( int i = 0; i 10; i++){
10 p i l a . push ( i ) ;
11 p i l a . imprime () ;
12 }
13 System . out . p r i n t l n ( ) ;
14
15 try{
16 // Se intenta eliminar once enteros
17 for ( int i = 0; i 10; i++){
18 Integer elemento = p i l a . pop () ;
19 System . out . p r i n t l n ( ”Elemento eliminado de l a p i l a : ” +
elemento ) ;
20 p i l a . imprime ( ) ;
21 }
22 }catch ( ExcepcionEDVacia e ) {
23 e . printStackTrace () ;
24 }
25 }
26 }
Ejemplo 6.4: Clase de prueba para PilaH
La salida del Ejemplo 6.4 se muestra en la Figura 6.5.
Consideraciones
Al menos en apariencia, el mecanismo de la herencia resulta sumamente
conveniente en base a lo expuesto con anterioridad; sin embargo, presenta
algunos inconvenientes que vale la pena considerar.
Las instancias de la clase PilaH, al heredar las caracterı́sticas y el compor-
tamiento inherentes a una lista enlazada, pueden hacer uso de los métodos de
inserción y de eliminación correspondientes a una lista enlazada, por lo que
desde esta perspectiva, un objeto de dicha clase podrı́a permitir inserciones
y eliminaciones, no únicamente del tope de la pila (representado por inicio),
sino también de la base de la pila (“representada”por fin) a la que se supone,
por definición, no se debe tener acceso.

137. 114 CAPÍTULO 6. LISTAS ENLAZADAS
Figura 6.5: Salida del Ejemplo 6.4

138. 6.3. HERENCIA VS. COMPOSICIÓN 115
Figura 6.6: Diagrama de clases UML para la implementación de una pila
utilizando composición y una lista lista enlazada
Tome en consideración que todavı́a se podrı́a transgredir más la defini-
ción de una pila, ya que potencialmente es posible insertar en, o eliminar de
cualquier parte de la estructura de datos con las modificaciones correspon-
dientes, lo cual queda completamente fuera tanto de la definición que se hizo
de la pila, como de las operaciones primitivas que le fueron definidas.
6.3.2. Implementación de una pila utilizando compo-
sición
La implementación de una pila utilizando el enfoque de composición, se
basa en la idea de que una lista enlazada, contiene ya definidas las operaciones
que necesita una pila, pero que también, como ya se discutió con anterioridad,
contiene otras operaciones que no deberı́an ser utilizadas por la misma.
En función de lo anterior y de manera conveniente, lo que se hace es
encapsular las operaciones de la lista enlazada dentro de las de la pila, con
la finalidad de proporcionar una interfaz o un conjunto de servicios ad hoc
con la definición de la estructura de datos en cuestión: la pila.
La Figura 6.6 muestra el diseño en diagrama de clases UML de la de-
finición de una pila que utiliza una lista enlazada para su implementación.

139. 116 CAPÍTULO 6. LISTAS ENLAZADAS
Observe y compare con detenimiento dicho diagrama con el de la Figura 6.4,
y note que el cambio principal está en la clase PilaC y en la relación entre
ésta y la clase Lista.
Por otro lado, la definición de la clase PilaC se muestra en el Ejemplo
6.5. Insto una vez más al lector a que ponga atención en dos aspectos:
1. La relación entre el diagrama de clases de la Figura 6.6 y el Ejemplo
6.5.
2. Los métodos push (lı́neas 16-18), pop (lı́neas 20-22) e imprime (lı́neas
24-26) no hacen otra cosa más que encapsular, de manera conveniente,
los mensajes enviados al objeto tope (lı́nea 6), mismos que son llevados
a cabo por los métodos correspondientes definidos en la clase Lista.
1 /∗ Clase que implementa una p i l a de o b j e t o s nodo de l a c l a s e NodoGT,
2 u t i l i z a n d o composicion y una l i s t a enlazada .
3 @autor Ricardo Ruiz Rodriguez
4 ∗/
5 public class PilaCT{
6 private Lista T tope ;
7
8 public PilaC () {
9 this ( ” Pila generica ” ) ;
10 }
11
12 public PilaC ( String n) {
13 tope = new Lista T(n) ;
14 }
15
16 public void push (T elemento ) {
17 tope . i n s e r t a A l I n i c i o ( elemento ) ;
18 }
19
20 public T pop () throws ExcepcionEDVacia{
21 return tope . e l i m i n a D e l I n i c i o ( ) ;
22 }
23
24 public void imprime ( ) {
25 tope . imprime ( ) ;
26 }
27 }
Ejemplo 6.5: Definición de la clase PilaC que implementa una pila de objetos
genéricos utilizando composición y una lista enlazada
En base a lo anterior, los objetos instanciados de la clase PilaC, sólo
podrán acceder a los servicios definidos explı́citamente en dicha clase y a
ningún otro más, lo cuál hace que, desde el punto de vista de la abstracción

140. 6.4. LISTAS CIRCULARES 117
y la representación de la estructura de datos, el enfoque de la composición
sea mucho más conveniente que el de la herencia.
La clase de prueba del Ejemplo 6.5 se muestra en el Ejemplo 6.6, y sigue
el mismo mecanismo de inserción de los ejemplos de prueba anteriores.
1 /∗ Clase de prueba para PilaC .
2 @autor Ricardo Ruiz Rodriguez
3 ∗/
4 public class PruebaPilaC{
5 public static void main ( String [ ] args ) {
6 PilaCInteger p i l a = new PilaCInteger () ;
7
8 // Se insertan diez enteros
9 for ( int i = 0; i 10; i++){
10 p i l a . push ( i ) ;
11 p i l a . imprime () ;
12 }
13 System . out . p r i n t l n ( ) ;
14
15 try{
16 // Se intenta eliminar once enteros
17 for ( int i = 0; i 10; i++){
18 Integer elemento = p i l a . pop () ;
19 System . out . p r i n t l n ( ”Elemento eliminado de l a p i l a : ” +
elemento ) ;
20 p i l a . imprime ( ) ;
21 }
22 }catch ( ExcepcionEDVacia e ) {
23 e . printStackTrace () ;
24 }
25 }
26 }
Ejemplo 6.6: Clase de prueba para PilaC
Finalmente, compruebe que la salida del Ejemplo 6.6 coincide exacta-
mente con la mostrada en la Figura 6.5, la cual se presentó también como la
salida correspondiente para el Ejemplo 6.4.
6.4. Listas circulares
Las listas enlazadas, también denominadas listas simplemente enlazadas,
son sumamente útiles y convenientes para diferentes usos y aplicaciones, al-
gunas de las cuales se expusieron en la secciones anteriores; sin embargo,
como casi todo en la vida, presentan ciertos inconvenientes.
Algunos de los inconvenientes que se tienen con una lista simplemente
enlazada son:

141. 118 CAPÍTULO 6. LISTAS ENLAZADAS
Figura 6.7: Abstracción de una lista enlazada circular como una secuencia de
nodos
Dada una única referencia a un nodo determinado de la lista enlazada,
y suponiendo que éste no sea el primero, no se puede llegar a ninguno
de los nodos que lo preceden.
Si por una determinada razón se recorre la lista enlazada, siempre debe
conservarse una referencia externa4
al inicio de dicha lista enlazada,
con la finalidad de poder volver a recorrer la lista nuevamente, en caso
de ser necesario.
En base a lo anterior, considere la siguiente modificación respecto a la
estructura de una lista simplemente enlazada:
El elemento siguiente en el último nodo, hará referencia al primer
nodo y no a null; a diferencia de lo que se define para una lista
simplemente enlazada convencional.
Al tipo de lista enlazada que adopta dicha modificación se le denomina
lista enlazada circular, y su representación se muestra en la Figura 6.7.
Es importante hacer notar que en una lista enlazada circular, es posible
llegar a cualquier otro nodo de la estructura de datos, partiendo de un no-
do distinto cualquiera, lo cual subsana los dos inconvenientes enunciados al
principio, para una lista simplemente enlazada.
Observe también que una lista enlazada circular no tiene un “primer” o
“último” nodo natural, por lo que se debe establecer un primer y último nodo
por convención5
.
Finalmente, tome en cuenta que una referencia a null, representa una lista
circular vacı́a. En la sección de ejercicios tendrá oportunidad de experimentar
con la implementación de dicha estructura de datos.
4
Además de la que se utilizó para el recorrido.
5
Lo cual es más una conveniencia, que una caracterı́stica inherente a la estructura de
datos.

142. 6.5. LISTAS DOBLEMENTE ENLAZADAS 119
6.4.1. El problema de Josephus
El siguiente es problema clásico, y su solución utilizando listas enlazadas
circulares, es una aplicación clave:
Un grupo de soldados se encuentra rodeado por una abruma-
dora fuerza enemiga. No hay esperanza de victoria sin refuerzos.
Lamentablemente, sólo hay un caballo disponible para ir en su
busca (o escapar).
Los soldados realizan un pacto de sangre para determinar cuál
de ellos tomará el caballo y, en el mejor de los casos, pedirá ayu-
da. Para ello, forman un cı́rculo y van eligiendo un número de
un sombrero (n). También se elige uno de los nombres de los
soldados, de otro sombrero.
Iniciando con el soldado cuyo nombre se eligió, se empieza
a contar en el sentido de las manecillas del reloj alrededor del
cı́rculo. Cuando la cuenta llega a n, el soldado correspondiente
se retira del cı́rculo y la cuenta vuelve a empezar con el soldado
siguiente.
El proceso continúa de manera análoga hasta que sólo queda
un soldado, el cuál será el que va a tomar el caballo y pedirá ayuda
(o escapará trágica e irremediablemente).
En resumen el problema de Josephus es: dado un número n, el ordena-
miento de los soldados en el cı́rculo, y el soldado a partir del que comienza
la cuenta, determinar:
El orden en el cual se eliminan los soldados del cı́rculo.
Cuál soldado escapa.
La solución al problema de Josephus, se deja como ejercicio para el lector.
6.5. Listas doblemente enlazadas
Aunque una lista enlazada circular tiene ventajas sobre una lista simple-
mente enlazada6
, tiene también algunas desventajas:
6
Dichas ventajas se comentaron en la sección anterior.

143. 120 CAPÍTULO 6. LISTAS ENLAZADAS
No es posible recorrer la lista enlazada circular hacia atrás (o hacia la
izquierda), es decir, sólo puede recorrerse en un sentido.
Dada una referencia a un nodo determinado de la lista enlazada cir-
cular, no es posible eliminar dicho nodo utilizando únicamente dicha
referencia (¿Por qué?).
Una estructura de datos conveniente para subsanar dichas desventajas,
es precisamente, la lista doblemente enlazada.
6.5.1. Definición, primitivas y representación
Una lista doblemente enlazada es una colección lineal de nodos auto
referidos, en donde cada nodo tiene dos referencias:
1. Una referencia al sucesor del nodo actual (siguiente).
2. Una referencia al antecesor del nodo actual (anterior).
La representación de una lista doblemente enlazada se muestra en la Fi-
gura 6.8 (a). Observe cómo al igual que en una lista enlazada, una lista
doblemente enlazada puede ser también doblemente enlazada circular (Fi-
gura 6.8 (b)). Esta última, sigue también las mismas consideraciones que se
hicieron en su momento para una lista enlazada.
Adicionalmente, las operaciones primitivas para una lista doblemente en-
lazada son exactamente las mismas que para una lista enlazada.
El diagrama de clases UML para una lista doblemente enlazada se pre-
senta en la Figura 6.9, el cual complementa la definición a través del corres-
pondiente diseño de clases.
Por ultimo, note que dicho diagrama presentado en la Figura 6.9 es sus-
tancialmente distinto de los que en general se han utilizado para el diseño
de las anteriores estructuras de datos, y que con excepción de la clase Ex-
cepcionEDVacia, tanto la clase ListaDoble como la clase NodoDobleG, han
sufrido cambios significativos. Consulte el ejercicio 8 para una ampliación al
respecto.

144. 6.5. LISTAS DOBLEMENTE ENLAZADAS 121
(a) Simple
(b) Circular
Figura 6.8: Abstracción de una lista doblemente enlazada
Figura 6.9: Diagrama de clases UML para una lista doblemente enlazada

145. 122 CAPÍTULO 6. LISTAS ENLAZADAS
6.6. Consideraciones finales
Una de las aplicaciones más útiles de las colas, las colas de prioridad y
de las listas vinculadas es la simulación.
Un programa de simulación modela una situación del mundo real para
aprender algo de ella. Cada objeto y acción del mundo tiene su representación
en el programa.
Si la simulación es precisa, el resultado del programa reflejará el resultado
de las acciones que se simulan, por lo que será posible comprender lo que ocu-
rre en una situación del mundo real sin necesidad de observar su ocurrencia
en el mundo real.
Algunos de los contextos en los que es posible aplicar técnicas de simula-
ción utilizando las estructuras de datos anteriormente mencionadas son:
Bancos.
Lı́neas aéreas.
Casetas de cobro de autopistas.
Terminal de autobuses.
Un largo etcétera.
Las listas enlazadas completan el espectro de estructuras de datos lineales
que se inició con las pilas, y es de notarse que se ha ido avanzando de lo
particular, hacia lo general, ya que como pudo apreciarse, las listas enlazadas
son las estructuras de datos que menos restricciones tienen en su definición
y operaciones.
Tanto los usos como las aplicaciones de las pilas, las colas de espera y
las listas enlazadas son prácticamente infinitas, limitadas únicamente, por la
imaginación del programador.

146. 6.7. EJERCICIOS 123
6.7. Ejercicios
1. Considerando la definición de una lista enlazada, modifique el Ejemplo
6.1 para que:
a) Incorpore un atributo privado numérico (n), que lleve el control del
número de elementos insertados en la lista enlazada. Al respecto
no olvide:
1) Inicializar explı́citamente dicho atributo a cero en el construc-
tor.
2) Proporcionar únicamente el método de tipo get para el atri-
buto n: obtenN().
b) Considere otras operaciones de inserción para la lista enlazada,
como por ejemplo:
insertaDespuesDe(e1, e2) inserta al elemento e1 después del
elemento e2.
Si e1 pudo ser insertado, se debe regresar un valor entero
distinto de cero para notificar éxito. En caso contrario7
, se
deberá regresar cero.
insertaAntesDe(e1, e2) inserta al elemento e1 antes del ele-
mento e2.
Si e1 pudo ser insertado, se debe regresar un valor entero
distinto de cero para notificar éxito. En caso contrario8
, se
deberá regresar cero.
insertaOrdenado(elemento) inserta al elemento en orden as-
cendente dentro de la lista.
De preferencia genere, como parte de su diseño, el diagrama de clases
UML para la nueva definición de la lista enlazada. Puede apoyarse de
los diagramas de clases de la Figura 6.2, y el de la Figura 6.9.
2. Modifique el Ejemplo 6.2, para que almacene otro tipo de objetos
además de los de la clase Integer. Pruebe con al menos las siguientes
clases:
7
Quizá el elemento e2 ni siquiera exista dentro de la lista enlazada.
8
Ídem.

147. 124 CAPÍTULO 6. LISTAS ENLAZADAS
Float.
String.
Persona (del Ejemplo 2.11 del Capı́tulo 2).
Cientifico (del Ejemplo 2.12 del Capı́tulo 2).
3. En el texto se hace mención de los inconvenientes de la implementación
de una pila por medio de la herencia de una lista enlazada. Compruebe
con al menos un ejemplo, la posibilidad de realizar una operación no
válida para una pila. Puede basarse en el Ejemplo 6.4.
4. En base a lo descrito en el texto, realice la implementación de una
cola de espera utilizando una lista enlazada. Para lo anterior, siga los
enfoques de:
a) Herencia (apóyese del Ejemplo 6.3).
b) Composición (apóyese del Ejemplo 6.5).
Determine sus propias conclusiones respecto al mecanismo de herencia
vs. composición para ambos tipos de implementación.
5. Modifique el Ejemplo 6.4 y el Ejemplo 6.6 para realizar las clases de
pruebas respectivas del Ejercicio 4.
Posteriormente, asegúrese de que es posible almacenar otro tipo de
objetos además de los de la clase Integer. Pruebe con al menos las
siguientes clases:
Float.
String.
Persona (del Ejemplo 2.11 del Capı́tulo 2).
Cientifico (del Ejemplo 2.12 del Capı́tulo 2).
6. En base a la descripción hecha en el texto ¿Cuáles son las consideracio-
nes necesarias para la implementación de una lista enlazada circular?
¿Cómo deben hacerse las inserciones? ¿Cómo deben hacerse las elimina-
ciones? ¿Cuáles serı́an las operaciones primitivas respecto de una lista
simplemente enlazada? ¿Qué otras operaciones, además de las presen-
tadas en el texto se podrı́an definir?

148. 6.7. EJERCICIOS 125
Implemente una lista enlazada circular y pruébela, ya que será necesaria
para la solución del siguiente ejercicio.
7. Utilice la implementación de la lista enlazada circular del ejercicio an-
terior para resolver el problema de Josephus descrito en el texto. Para
ello:
a) Considere que existen N soldados. Para cada uno de los cuales,
deberá solicitar su nombre, por lo que se recomienda que la lista
enlazada circular almacene objetos de la clase String.
b) En cada iteración (determinación de la eliminación de un soldado),
genere un número aleatorio n, donde n ∈ [1 . . . N].
c) De manera paralela al almacenamiento de los soldados en la lista
enlazada circular, almacene el nombre de los soldados en un arre-
glo9
y genere un número aleatorio m, (distinto a n), de tal forma
que m sea el ı́ndice correspondiente al arreglo de nombres de los
soldados, y servirá para elegir al soldado inicial. Tome en cuenta
que m ∈ [0 . . . N − 1].
8. En base a la descripción y la definición de una lista doblemente enlazada
que se realizó en la sección correspondiente, y considerando lo descrito
en el diagrama de clases UML de la Figura 6.9, implemente una lista
doblemente enlazada.
Para realizar lo anterior, considere la siguiente descripción para los
métodos correspondientes:
insertaAlInicio(elemento) agrega a elemento al inicio de la lista
doblemente enlazada.
insertaAlFinal(elemento) agrega a elemento al fin de la lista doble-
mente enlazada.
eliminaDelInicio() elimina un elemento del inicio de la lista doble-
mente enlazada.
eliminaDelFinal() elimina un elemento del fin de la lista doblemente
enlazada.
9
Puede consultar el Apéndice A para consultar el manejo de arreglos.

149. 126 CAPÍTULO 6. LISTAS ENLAZADAS
estaVacia() regresa verdadero o falso, dependiendo de si la lista do-
blemente enlazada contiene o no elementos respectivamente.
imprime() imprime en la salida estándar (pantalla) los elementos de
la lista doblemente enlazada.
obtenN() regresa el número de elementos actualmente almacenados
en la lista doblemente enlazada.
insertaDespuesDe(e1, e2) inserta al elemento e1 después del ele-
mento e2. Si e1 pudo ser insertado, se debe regresar un valor
entero distinto de cero para notificar éxito. En caso contrario10
, se
deberá regresar cero.
insertaAntesDe(e1, e2) inserta al elemento e1 antes del elemento
e2. Si e1 pudo ser insertado, se debe regresar un valor entero
distinto de cero para notificar éxito. En caso contrario11
, se de-
berá regresar cero.
insertaOrdenado(elemento) inserta al elemento en orden ascenden-
te dentro de la lista doblemente enlazada.
9. En base a la implementación de la lista doblemente enlazada del Ejerci-
cio 8 ¿Qué cambios habrı́a que realizar para la implementación de una
lista doblemente enlazada circular?
10. Considere las siguientes fórmulas:
Promedio
xprom =
n
i=1 xi
n
(6.1)
Desviación estándar
σ =
n
i=1(xi − xprom)2
n − 1
(6.2)
donde n es el número de elementos en el conjunto de datos y x es
un dato del conjunto.
10
Quizá el elemento e2 ni siquiera exista dentro de la lista doblemente enlazada.
11
Ídem.

150. 6.7. EJERCICIOS 127
Regresión lineal
β1 =
(
n
i=1 xiyi) − (nxpromyprom)
(
n
i=1 x2
i ) − (nx2
prom)
(6.3)
β0 = yavg − β1xavg (6.4)
Para dos conjuntos de datos A y B, donde n es el número de
elementos en ambos conjuntos, i.e. xi ∈ A y yi ∈ B.
Coeficiente de correlación
r =
n(
n
i=1 xiyi) − (
n
i=1 xi)(
n
i=1 yi)
[n(
n
i=1 x2
i ) − (
n
i=1 xi)2][n(
n
i=1 y2
i ) − (
n
i=1 yi)2]
(6.5)
Utilizando la implementación de la lista doblemente enlazada del Ejer-
cicio 8, escriba un programa que realice el cálculo de cada una de las
expresiones anteriores.
Sugerencia: formule cada una de las expresiones como un método.
11. Considere el Ejercicio 5 del Capı́tulo 5 y la Figura 6.10, en donde se
tiene una lista enlazada (vertical) con tres nodos, y en cada uno de
ellos, una referencia a una cola de espera representada en dicha figura
por inicio. Utilizando cada una de las colas de espera referidas por la
lista enlazada, implemente el algoritmo de Round robin.
La Figura 6.10 representa un estado determinado de tres colas de es-
pera con números enteros que representan las cantidades a considerar
(quantum).
La atención de los elementos formados en la cola de espera, consiste
en restarle uno al quantum del nodo que se encuentra al inicio de la
cola, y volverlo a formar al final de la misma para atender de manera
análoga a los siguientes nodos. Tome en consideración que, una vez que
el número llega a cero, el nodo correspondientes es eliminado.
La atención se realiza en base a la prioridad de los elementos de la
cola de espera, la cual está representada por los números 1, 2 y 3 de
la lista enlazada, donde 3 y 1 son la prioridad más alta y más baja
respectivamente. No es posible atender a los elementos formados en
un cola de espera cuya prioridad sea menor, si existen elementos que
necesitan ser atendidos en alguna cola de espera de mayor prioridad.

151. 128 CAPÍTULO 6. LISTAS ENLAZADAS
Figura 6.10: Representación de Round robin por niveles de prioridad
El proceso anteriormente descrito continúa, hasta atender o despachar
a todos los nodos formados en las tres colas de espera. Para lo anterior,
considere:
a) Genere un número aleatorio entre 1 y 3, mismo que representará la
prioridad para seleccionar la cola de espera correspondiente.
b) Para cada cola de espera, genere un número aleatorio entre 10 y
50, el cual representará el número de nodos que contendrá la cola
de espera en cuestión.
c) Por cada nodo, genere nuevamente un número aleatorio entre 1 y
500, mismo que representará el quantum asignado a cada nodo.
No olvide construir también una clase de prueba para su implementa-
ción. La salida de su programa puede ser en la salida estándar o en un
archivo de texto.

152. Capı́tulo 7
Árboles binarios
Concision in style, precision in thought, decision in life.
Victor Hugo
7.1. Definición
Un árbol binario es un conjunto finito de elementos, el cual está vacı́o,
o dividido en tres subconjuntos disjuntos:
1. El primer subconjunto contiene un elemento único llamado raı́z del
árbol.
2. El segundo subconjunto es en sı́ mismo un árbol binario y se le conoce
como subárbol izquierdo del árbol original.
3. El tercer subconjunto es también un árbol binario y se le conoce como
subárbol derecho del árbol original.
Tome en consideración que en un árbol binario, el subárbol izquierdo o
el subárbol derecho podrı́an estar vacı́os.
7.1.1. Representación y conceptos
Respecto a su representación, es común denominar a cada elemento de
un árbol binario como nodo del árbol. La Figura 7.1 muestra una posible
representación para un árbol binario.
129

153. 130 CAPÍTULO 7. ÁRBOLES BINARIOS
Figura 7.1: Abstracción de un árbol binario como una estructura de nodos
Ahora bien, la representación de la Figura 7.1 resultará sumamente útil
para desarrollar e ilustrar los siguientes conceptos:
Si B es la raı́z de un árbol binario, y D es la raı́z del subárbol iz-
quierdo/derecho1
, se dice que B es el padre de D y que D es el hijo
izquierdo/derecho de B.
A un nodo que no tiene hijos, como los nodos A o C de la Figura 7.1,
se le conoce como nodo hoja.
Se dice que un nodo n1 es un ancestro de un nodo n2 (y que n2 es
un descendiente de n1) si n1 es el padre de n2 o el padre de algún
ancestro de n2.
Recorrer un árbol de la raı́z hacia las hojas se denomina descender
el árbol, y al sentido opuesto, ascender el árbol.
El nivel de un nodo en un árbol binario se define del modo siguiente:
1. La raı́z del árbol tiene el nivel 0.
2. El nivel de cualquier otro nodo en el árbol es uno más que el nivel
de su nodo padre.
1
Todos los conceptos que sigan esta notación, tienen una naturaleza simétrica debido
a la caracterı́stica inherente a los árboles, y por lo tanto, aplica tanto para el subárbol
izquierdo como para el subárbol derecho.

154. 7.1. DEFINICIÓN 131
La profundidad o altura de un árbol binario, es el máximo nivel de
cualquier hoja en el árbol.
Por otro lado, se dice que un árbol estrictamente binario es aquel en
el que cada nodo que no es hoja, tiene sus subárboles izquierdo y derecho no
vacı́os. En términos coloquiales, un árbol estrictamente binario es un árbol
binario en el que cada nodo, tiene dos hijos o simplemente no tiene, es decir,
no se vale tener un solo hijo: dos o nada.
De lo anterior, observe que un árbol estrictamente binario con n hojas,
siempre contiene 2n-1 nodos (¿Por qué?).
Otro tipo de árboles binarios son los árboles binarios completos. Un árbol
binario completo de profundidad p, es un árbol estrictamente binario que
tiene todas sus hojas en el nivel p.
7.1.2. Operaciones primitivas
Respecto a las operaciones primitivas para un árbol binario, considere lo
siguiente. Sea p una referencia a un nodo cualquiera (nd) de un árbol binario.
Se definen las siguientes operaciones primitivas sobre dicho árbol:
obtenDato regresa el contenido (datos) de nd cuando se le envı́a el mensaje
correspondiente al objeto p, es decir:
p.obtenDato()
obtenNodoIzquierdo regresa una referencia al hijo izquierdo de nd cuando
se le envı́a el mensaje correspondiente al objeto p, es decir:
p.obtenNodoIzquierdo()
obtenNodoDerecho regresa una referencia al hijo derecho de nd cuando
se le envı́a el mensaje correspondiente al objeto p, es decir:
p.obtenNodoDerecho()
estableceDato asigna un valor especı́fico representado por d a nd, cuando
se le envı́a el mensaje correspondiente al objeto p, es decir:
p.estableceDato(d)
estableceNodoIzquierdo asigna un nodo representado por n, como hijo
izquierdo de nd cuando se le envı́a el mensaje respectivo al objeto p,
es decir:
p.estableceNodoIzquierdo(n)

155. 132 CAPÍTULO 7. ÁRBOLES BINARIOS
estableceNodoDerecho asigna un nodo representado por n, como hijo de-
recho de nd cuando se le envı́a el mensaje respectivo al objeto p, es
decir:
p.estableceNodoDerecho(n)
Por otro lado y siguiendo las consideraciones planteadas con anterioridad,
algunas otras operaciones que podrı́an ser útiles en la implementación de un
árbol binario, son las siguientes:
1. La operación padre regresa una referencia al padre de nd.
2. La operación hermano regresa una referencia al hermano de nd.
3. La operación esIzquierdo regresa true si nd es un hijo izquierdo de
algún otro nodo en el árbol binario, y false en caso contrario.
4. La operación esDerecho regresa true si nd es un hijo derecho de algún
otro nodo en el árbol binario, y false en caso contrario.
Dichas operaciones no son las únicas posibles; sin embargo, son deseables
como los servicios adicionales que podrı́a proporcionar un árbol binario.
Recorridos
Una operación muy común en un árbol binario, es la de recorrer todo el
árbol en un orden especı́fico pero ¿Cuál serı́a el orden natural de recorrido
de un árbol binario? Piense por un momento en ello.
A la operación de recorrer un árbol binario de una forma especı́fica y de
numerar o visitar sus nodos, se le conoce como visitar el árbol, es decir,
procesar el valor o dato de cada uno de los nodos, para realizar algo con él.
En general, se definen tres métodos de recorrido sobre un árbol binario,
y para ello, se deberán tomar en cuenta las siguientes consideraciones:
1. No se necesita hacer nada para un árbol binario vacı́o.
2. Todos los métodos se definen recursivamente.
3. Siempre se recorren la raı́z y los subárboles izquierdo y derecho, la
diferencia radica en el orden en que se visitan.

156. 7.1. DEFINICIÓN 133
Para recorrer un árbol binario no vacı́o en orden previo (orden de pri-
mera profundidad), se ejecutan tres operaciones:
1. Visitar la raı́z.
2. Recorrer el subárbol izquierdo en orden previo.
3. Recorrer el subárbol derecho en orden previo.
Ahora bien, para recorrer un árbol binario no vacı́o en orden (orden
simétrico), se ejecutan tres operaciones:
1. Recorrer el subárbol izquierdo en orden.
2. Visitar la raı́z.
3. Recorrer el subárbol derecho en orden.
Finalmente, para recorrer un árbol binario no vacı́o en orden posterior,
se ejecutan tres operaciones:
1. Recorrer el subárbol izquierdo en orden posterior.
2. Recorrer el subárbol derecho en orden posterior.
3. Visitar la raı́z.
Tome en consideración que los tres recorridos anteriormente descritos,
son únicamente tres posibilidades de las seis posibles, sin embargo, son los
recorridos más comunes.
Los otros tres recorridos posibles se describen a continuación, y a falta de
un mejor nombre, se les denominará recorridos inversos.
Para recorrer un árbol binario no vacı́o en orden previo inverso, se
ejecutan tres operaciones:
1. Visitar la raı́z.
2. Recorrer el subárbol derecho en orden previo inverso.
3. Recorrer el subárbol izquierdo en orden previo inverso.

157. 134 CAPÍTULO 7. ÁRBOLES BINARIOS
Por otro lado, para recorrer un árbol binario no vacı́o en orden inverso,
se ejecutan tres operaciones:
1. Recorrer el subárbol derecho en orden inverso.
2. Visitar la raı́z.
3. Recorrer el subárbol izquierdo en orden inverso.
Finalmente, para recorrer un árbol binario no vacı́o en orden posterior
inverso, se ejecutan tres operaciones:
1. Recorrer el subárbol derecho en orden posterior inverso.
2. Recorrer el subárbol izquierdo en orden posterior inverso.
3. Visitar la raı́z.
7.2. Árbol binario de búsqueda (ABB)
Un árbol binario es una estructura de datos sumamente útil en muchos
aspectos, en particular, cuando deben tomarse decisiones en dos sentidos, en
cada punto de un proceso determinado.
En base a lo anterior, suponga que por alguna razón se desea encontrar
todos los duplicados de una secuencia de números. Para ello, considere lo
siguiente:
1. El primer número de la secuencia, se coloca en un nodo que se ha
establecido como la raı́z de un árbol binario, cuyos subárboles izquierdo
y derecho están inicialmente vacı́os.
2. Cada número sucesivo en la secuencia se compara con el número que
se encuentra en la raı́z del árbol binario. En este momento, se tienen
tres casos a considerar:
a) Si coincide, se tiene un duplicado.
b) Si es menor, se examina el subárbol izquierdo.
c) Si es mayor, se examina el subárbol derecho.

158. 7.2. ÁRBOL BINARIO DE BÚSQUEDA (ABB) 135
3. Si alguno de los subárboles esta vacı́o, el número no es un duplicado y
se coloca en un nodo nuevo en dicha posición del árbol binario.
4. Si el subárbol correspondiente no está vacı́o, se compara el número con
la raı́z del subárbol en cuestión, y se repite todo el proceso nuevamente
con dicho subárbol.
Un árbol binario de búsqueda (ABB) es un árbol binario que no tiene
valores duplicados en los nodos, y además, tiene las siguientes caracterı́sticas:
1. Los valores en cualquier subárbol izquierdo son menores que el valor
en su nodo padre.
2. Los valores en cualquier subárbol derecho son mayores que el valor en
su nodo padre.
Tome en cuenta que un ABB es un árbol binario, pero un árbol binario
no es necesariamente un ABB. En este sentido, todo lo que se ha dicho y
definido para árboles binarios, es aplicable también a los árboles binarios de
búsqueda.
7.2.1. Operaciones primitivas
Respecto a las operaciones primitivas, se definen cuatro operaciones pri-
mitivas para un ABB:
inserta inserta un nuevo nodo al árbol binario de búsqueda. La inserción
se realiza de manera ordenada respecto del elemento a insertar, por lo
que debe existir una relación de orden para dicho elemento.
En resumen, la operación inserta de manera ordenada a elemento en el
ABB cuando el objeto abb recibe el mensaje correspondiente, es decir:
abb.inserta(elemento)
recorre en preorden recorre el ABB no vacı́o en orden previo, de tal
forma que cuando el objeto abb recibe el mensaje:
abb.recorrePreorden()
se imprime en la salida estándar el recorrido en orden previo de abb.

159. 136 CAPÍTULO 7. ÁRBOLES BINARIOS
recorrido en orden recorre el árbol binario de búsqueda no vacı́o en or-
den, de tal forma que cuando el objeto abb recibe el mensaje:
abb.recorreEnorden()
se imprime en la salida estándar el recorrido en orden de abb.
Note cómo un recorrido en orden, como su nombre lo indica, imprime
en la salida estándar los elementos almacenados en el árbol de manera
ascendente.
recorrido en postorden recorre el ABB no vacı́o en orden posterior, de
tal forma que cuando el objeto abb recibe el mensaje:
abb.recorrePostorden()
se imprime en la salida estándar el recorrido en orden posterior de abb.
Para el caso de un árbol binario de búsqueda, también serı́an deseables
otras operaciones, como aquellas que se definieron para los árboles binarios:
primitivas, adicionales y recorridos inversos por ejemplo.
En éste sentido, es importante resaltar que siempre que una operación
no viole la relación de orden intrı́nseca a los ABB, es factible de ser imple-
mentada, aunque la decisión respecto a su implementación, estará en función
directa de su correspondiente aplicación.
7.2.2. Representación
La representación de un árbol binario que se presentó en la Figura 7.1, es
en realidad un árbol binario de búsqueda.
Para complementar dicha abstracción, el diagrama de clases UML de la
Figura 7.2 muestra otro tipo de representación para un ABB desde el punto
de vista del diseño.
Observe cómo ha cambiado por completo la representación del nodo utili-
zado para un árbol binario de búsqueda (NodoABB), en comparación con el
nodo que se habı́a estado utilizando (NodoG) para las anteriores estructuras
de datos presentadas en el libro.
La clase NodoABB de la Figura 7.2 define los atributos correspondientes
para los subárboles izquierdo y derecho2
, y el dato a almacenar (dato). Adi-
cionalmente, la clase define los servicios que deberá implementar la clase, los
cuales corresponden a los métodos de tipo set y get.
2
Representados por los atributos nodoIzquierdo y nodoDerecho respectivamente.

160. 7.2. ÁRBOL BINARIO DE BÚSQUEDA (ABB) 137
Figura 7.2: Diagrama de clases UML para un árbol binario de búsqueda
Por otro lado, la clase ABB describe la abstracción correspondiente para
la implementación del árbol binario de búsqueda, y define como servicios, las
operaciones primitivas definidas con anterioridad para un ABB.
Tanto la definición en un diagrama de clases UML, como la implementa-
ción correspondiente de los recorridos inversos, se dejan como ejercicio para
el lector.
7.2.3. Implementación
Esta sección presenta la implementación de un ABB en base a dos enfo-
ques respecto a la inserción de elementos:
1. Enfoque recursivo.
2. Enfoque iterativo.
Para ambas implementaciones, se utiliza la clase NodoABB definida en
el Ejemplo 7.1, por lo que será la primera que se describa.
La clase NodoABB define un nodo capaz de almacenar objetos genéricos.
Cada nodo definido por la clase, tiene la forma de cada uno de los nodos de la
Figura 7.1. Observe además que cada objeto instanciado tendrá dos referen-
cias a objetos como él, las cuales representarán referencias hacia el subárbol
izquierdo (nodoIzquierdo) y hacia el subárbol derecho (nodoDerecho).
Los detalles restantes deberı́an resultarle familiares al lector, ya que en
esencia se refieren a un constructor y a los métodos de tipo set y get para
cada uno de los atributos.

161. 138 CAPÍTULO 7. ÁRBOLES BINARIOS
1 /∗ Clase que implementa o b j e t o s nodo genericos para un ABB.
2 @autor Ricardo Ruiz Rodriguez
3 ∗/
4 class NodoABBT extends ComparableT{
5 private NodoABBT nodoIzquierdo ;
6 private T dato ;
7 private NodoABBT nodoDerecho ;
8
9 public NodoABB(T d) {
10 dato = d ;
11 nodoIzquierdo = nodoDerecho = null ;
12 }
13
14 public void estableceDato (T d) {
15 dato = d ;
16 }
17
18 public T obtenDato () {
19 return dato ;
20 }
21
22 public void estableceNodoIzquierdo (NodoABBT n) {
23 nodoIzquierdo = n ;
24 }
25
26 NodoABBT obtenNodoIzquierdo () {
27 return nodoIzquierdo ;
28 }
29
30 public void estableceNodoDerecho (NodoABBT n) {
31 nodoDerecho = n ;
32 }
33
34 NodoABBT obtenNodoDerecho () {
35 return nodoDerecho ;
36 }
37 }
Ejemplo 7.1: Definición de la clase NodoABB que permite representar objetos
(nodos) genéricos para un árbol binario de búsqueda
Asegúrese de comprender el Ejemplo 7.1 en su totalidad antes de conti-
nuar.
Enfoque recursivo
Probablemente el enfoque más común para la implementación de un ABB
debido a la naturaleza inherente a la definición de dicha estructura de datos,
sea el enfoque basado en la recursividad.
El Ejemplo 7.2 muestra la definición de la clase ABBr, la cual es en
esencia la implementación de la representación definida en el diagrama de

162. 7.2. ÁRBOL BINARIO DE BÚSQUEDA (ABB) 139
clases UML de la Figura 7.2.
El estudio y la comprensión de la implementación de los métodos de
recorrido para un árbol binario de búsqueda (lı́neas 34-68), se dejan como
ejercicio para el lector.
El método inserta (lı́neas 13-18), crea la raı́z del árbol (lı́nea 15) si el
ABB está vacı́o (lı́nea 14), i.e. no existe. En caso contrario, delega la res-
ponsabilidad de la inserción de elemento dentro de arbol, al método privado
recursivo insertaR (lı́nea 17).
1 /∗ Clase que implementa un ABB con o b j e t o s NodoABB.
2 Implementa l o s recorridos en orden , preorden y postorden .
3 @autor Ricardo Ruiz Rodriguez
4 ∗/
5 public class ABBrT extends ComparableT{
6 private NodoABBT arbol ;
7
8 public ABBr() {
9 arbol = null ;
10 }
11
12 // i n s e r t a un nuevo nodo en e l ABB
13 public void i n s e r t a (T elemento ) {
14 i f ( arbol == null )
15 arbol = new NodoABBT(elemento ) ;
16 else
17 insertaR ( arbol , elemento ) ;
18 }
19
20 // i n s e r t a e l elemento de manera recursiva en e l ABB
21 private void insertaR (NodoABBT abb , T elemento ) {
22 i f ( elemento . compareTo ( abb . obtenDato ( ) ) 0) // subarbol i z q u i e r d o
23 i f ( abb . obtenNodoIzquierdo ( ) == null )
24 abb . estableceNodoIzquierdo (new NodoABBT(elemento ) ) ;
25 else // recorre e l arbol i z q u i e r d o de manera recursiva
26 insertaR ( abb . obtenNodoIzquierdo () , elemento ) ;
27 else i f ( elemento . compareTo ( abb . obtenDato ( ) ) 0 ) // subarbol derecho
28 i f ( abb . obtenNodoDerecho () == null )
29 abb . estableceNodoDerecho (new NodoABBT(elemento ) ) ;
30 else // recorre e l arbol derecho de manera recursiva
31 insertaR ( abb . obtenNodoDerecho ( ) , elemento ) ;
32 }
33
34 public void recorrePreorden () {
35 preorden ( arbol ) ;
36 }
37
38 private void preorden (NodoABBT nodo ) {
39 i f ( nodo == null )
40 return ;
41 System . out . print ( nodo . obtenDato () + ” ” ) ; // v i s i t a e l nodo
42 preorden ( nodo . obtenNodoIzquierdo () ) ; // recorre e l subarbol i z q u i e r d o
43 preorden ( nodo . obtenNodoDerecho ( ) ) ; // recorre e l subarbol derecho
44 }
45

163. 140 CAPÍTULO 7. ÁRBOLES BINARIOS
46 public void recorreEnorden () {
47 enorden ( arbol ) ;
48 }
49
50 private void enorden (NodoABBT nodo ) {
51 i f ( nodo == null )
52 return ;
53 enorden ( nodo . obtenNodoIzquierdo ( ) ) ; // recorre e l subarbol i z q u i e r d o
54 System . out . print ( nodo . obtenDato () + ” ” ) ; // v i s i t a e l nodo
55 enorden ( nodo . obtenNodoDerecho () ) ; // recorre e l subarbol derecho
56 }
57
58 public void recorrePostorden ( ) {
59 postorden ( arbol ) ;
60 }
61
62 private void postorden (NodoABBT nodo ) {
63 i f ( nodo == null )
64 return ;
65 postorden ( nodo . obtenNodoIzquierdo () ) ; // recorre e l subarbol i z q u i e r d o
66 postorden ( nodo . obtenNodoDerecho () ) ; // recorre e l subarbol derecho
67 System . out . print ( nodo . obtenDato () + ” ” ) ; // v i s i t a e l nodo
68 }
69 }
Ejemplo 7.2: Definición de la clase ABBr que permite almacenar nodos
(NodoABB) en un árbol binario de búsqueda
Por su parte, la idea del método insertaR (lı́neas 21-32) es verificar la
relación de orden de elemento respecto del dato almacenado en el nodo actual,
y entonces:
Si elemento es menor (lı́nea 22), debe ser insertado en el subárbol iz-
quierdo.
Si el subárbol izquierdo está vacı́o o disponible (lı́nea 23), se crea un
nuevo nodo con elemento como dato y se asigna como hijo izquierdo
(lı́nea 24). Si no está vacı́o (lı́nea 25), se recorre el subárbol izquierdo de
manera recursiva (lı́nea 26) para encontrar la posición apropiada para
elemento dentro del árbol.
Si elemento es mayor (lı́nea 27), debe ser insertado en el subárbol de-
recho.
Si el subárbol derecho está vacı́o o disponible (lı́nea 28), se crea un
nuevo nodo con elemento como dato y se asigna como hijo derecho
(lı́nea 29). Si no está vacı́o (lı́nea 30), se recorre el subárbol derecho de

164. 7.2. ÁRBOL BINARIO DE BÚSQUEDA (ABB) 141
manera recursiva (lı́nea 31) para encontrar la posición apropiada para
elemento dentro del ABB.
La clase de prueba para la clase ABBr del Ejemplo 7.2, se muestra en el
Ejemplo 7.3.
1 /∗ Clase de prueba para un ABB implementando con r ec u r s iv id a d .
2 @autor Ricardo Ruiz Rodriguez
3 ∗/
4 import java . u t i l . Random ;
5
6 public class PruebaArbol{
7 public static void main ( String [ ] args ) {
8 ABBrInteger abb = new ABBrInteger () ;
9 Random numeroAleatorio = new Random() ;
10
11 System . out . p r i n t l n ( ”Numeros a i n s e r t a r (0−50) : ” ) ;
12 for ( int i = 1; i 11; i++){
13 // Numero a l e a t o r i o entre 0 y 50
14 int valor = numeroAleatorio . nextInt (51) ;
15 System . out . print ( valor + ” ” ) ;
16 abb . i n s e r t a ( valor ) ;
17 }
18
19 System . out . p r i n t l n ( ”n nRecorrido en pre orden : ” ) ;
20 abb . recorrePreorden ( ) ;
21
22 System . out . p r i n t l n ( ”n nRecorrido en orden : ” ) ;
23 abb . recorreEnorden () ;
24
25 System . out . p r i n t l n ( ”n nRecorrido en post orden : ” ) ;
26 abb . recorrePostorden () ;
27 System . out . p r i n t l n ( ) ;
28 }
29 }
Ejemplo 7.3: Clase de prueba para el árbol binario de búsqueda (recursivo)
La clase PruebaArbol del Ejemplo 7.3, utiliza la clase Random del API
para generar un número aleatorio (lı́nea 14) dentro de un rango especı́fico,
el cual, además de presentarse en la salida estándar (lı́nea 15), representa el
valor a ser insertado dentro del árbol binario de búsqueda (lı́nea 16).
Finalmente, el Ejemplo 7.3 realiza los tres recorridos más convencionales
definidos para un ABB (lı́neas 19-27). Es ampliamente recomendable que el
lector realice varias ejecuciones de la clase PruebaArbol, y corrobore la salida
con inserciones y recorridos realizados a papel y lápiz.
Una posible salida para el Ejemplo 7.3 se muestra en la Figura 7.3.

165. 142 CAPÍTULO 7. ÁRBOLES BINARIOS
Figura 7.3: Una posible salida para el Ejemplo 7.3 y el Ejemplo 7.5
Enfoque iterativo
Un enfoque alternativo para la implementación de la operación de in-
serción en un árbol binario de búsqueda, es utilizar un ciclo en lugar de
recursividad.
El enfoque propuesto es casi tan compacto como el recursivo, pero mucho
más eficiente. La implementación sin recursividad del ABB representado en
la Figura 7.2, se presenta en el Ejemplo 7.4.
Al igual que antes, el estudio y la comprensión de la implementación de
los métodos de recorrido (lı́neas 34-68), se dejan como ejercicio para el lector.
El método inserta (lı́neas 13-32), crea la raı́z del árbol (lı́nea 15) si el
ABB está vacı́o (lı́nea 14), i.e. no existe. En caso contrario, se genera una
referencia alterna (lı́nea 17) para recorrer el árbol (lı́nea 18).
Al igual que antes, la idea es verificar la relación de orden de elemento
respecto del dato almacenado en el nodo actual, y entonces:
Si elemento es menor (lı́nea 19), debe ser insertado en el subárbol iz-
quierdo.
Si el subárbol izquierdo está vacı́o o disponible (lı́nea 20), se crea un
nuevo nodo con elemento como dato y se asigna como hijo izquier-
do (lı́nea 21). Si no está vacı́o (lı́nea 22), se cambia la referencia del
subárbol en cuestión (abb), y se recorre el subárbol izquierdo (lı́nea 23)
para encontrar la posición apropiada para elemento dentro del árbol.

166. 7.2. ÁRBOL BINARIO DE BÚSQUEDA (ABB) 143
Si elemento es mayor (lı́nea 24), debe ser insertado en el subárbol de-
recho.
1 /∗ Clase que implementa un ABB con o b j e t o s NodoABB.
2 Implementa l o s recorridos en orden , preorden y postroden .
3 @autor Ricardo Ruiz Rodriguez
4 ∗/
5 public class ABB
T extends ComparableT{
6 private NodoABBT arbol ;
7
8 public ABB() {
9 arbol = null ;
10 }
11
12 // i n s e r t a un nuevo nodo en e l ABB
13 public void i n s e r t a (T elemento ) {
14 i f ( arbol == null )
15 arbol = new NodoABBT(elemento ) ;
16 else {
17 NodoABBT abb = arbol ;
18 while ( abb != null )
19 i f ( elemento . compareTo ( abb . obtenDato ( ) ) 0)
20 i f ( abb . obtenNodoIzquierdo ( ) == null )
21 abb . estableceNodoIzquierdo (new
NodoABBT(elemento ) ) ;
22 else
23 abb = abb . obtenNodoIzquierdo ( ) ;
24 else i f ( elemento . compareTo ( abb . obtenDato ( ) ) 0 )
25 i f ( abb . obtenNodoDerecho () == null )
26 abb . estableceNodoDerecho (new NodoABBT(elemento ) ) ;
27 else
28 abb = abb . obtenNodoDerecho ( ) ;
29 else
30 return ;
31 }
32 }
33
34 public void recorrePreorden () {
35 preorden ( arbol ) ;
36 }
37
38 private void preorden (NodoABBT nodo ) {
39 i f ( nodo == null )
40 return ;
41 System . out . print ( nodo . obtenDato () + ” ” ) ; // v i s i t a e l nodo
42 preorden ( nodo . obtenNodoIzquierdo () ) ; // recorre e l subarbol
i z q u i e r d o
43 preorden ( nodo . obtenNodoDerecho ( ) ) ; // recorre e l subarbol
derecho
44 }
45
46 public void recorreEnorden () {
47 enorden ( arbol ) ;
48 }
49
50 private void enorden (NodoABBT nodo ) {
51 i f ( nodo == null )

167. 144 CAPÍTULO 7. ÁRBOLES BINARIOS
52 return ;
53 enorden ( nodo . obtenNodoIzquierdo ( ) ) ; // recorre e l subarbol
i z q u i e r d o
54 System . out . print ( nodo . obtenDato () + ” ” ) ; // v i s i t a e l nodo
55 enorden ( nodo . obtenNodoDerecho () ) ; // recorre e l subarbol derecho
56 }
57
58 public void recorrePostorden ( ) {
59 postorden ( arbol ) ;
60 }
61
62 private void postorden (NodoABBT nodo ) {
63 i f ( nodo == null )
64 return ;
65 postorden ( nodo . obtenNodoIzquierdo () ) ; // recorre e l subarbol
i z q u i e r d o
66 postorden ( nodo . obtenNodoDerecho () ) ; // recorre e l subarbol
derecho
67 System . out . print ( nodo . obtenDato () + ” ” ) ; // v i s i t a e l nodo
68 }
69 }
Ejemplo 7.4: Definición de la clase ABB que permite almacenar nodos
(NodoABB) en un árbol binario de búsqueda
Si el subárbol derecho está vacı́o o disponible (lı́nea 25), se crea un nue-
vo nodo con elemento como dato y se asigna como hijo derecho (lı́nea
26). Si no está vacı́o (lı́nea 27), se cambia la referencia del subárbol en
cuestión (abb), y se recorre el subárbol derecho (lı́nea 28) para encon-
trar la posición apropiada para elemento dentro del ABB.
Finalmente, si el elemento no fue menor ni mayor, entonces es igual por
tricotomı́a, y no hay nada por hacer mas que terminar (lı́neas 29 y 30).
La clase de prueba para la clase ABB del Ejemplo 7.4, se muestra en el
Ejemplo 7.5.
Al igual que antes, la clase PruebaABB del Ejemplo 7.5 utiliza la clase
Random del API para generar un número aleatorio (lı́nea 14) dentro de un
rango especı́fico, el cual además de presentarse en la salida estándar (lı́nea
15), representa el valor que será insertado dentro del árbol binario de búsque-
da (lı́nea 16).
Finalmente, el Ejemplo 7.5 también realiza los tres recorridos más conven-
cionales definidos para un ABB (lı́neas 19-27). Una vez más, se recomienda
ampliamente que el lector realice varias ejecuciones de la clase PruebaABB,
y corrobore la salida con inserciones y recorridos realizados a papel y lápiz
(ver Figura 7.3).

168. 7.2. ÁRBOL BINARIO DE BÚSQUEDA (ABB) 145
1 /∗ Clase de prueba para un ABB implementando con r ec u r s iv id a d .
2 @autor Ricardo Ruiz Rodriguez
3 ∗/
4 import java . u t i l . Random ;
5
6 public class PruebaABB{
7 public static void main ( String [ ] args ) {
8 ABB
Integer abb = new ABB
Integer () ;
9 Random numeroAleatorio = new Random() ;
10
11 System . out . p r i n t l n ( ”Numeros a i n s e r t a r (0−50) : ” ) ;
12 for ( int i = 1; i 11; i++){
13 // Numero a l e a t o r i o entre 0 y 50
14 int valor = numeroAleatorio . nextInt (51) ;
15 System . out . print ( valor + ” ” ) ;
16 abb . i n s e r t a ( valor ) ;
17 }
18
19 System . out . p r i n t l n ( ”n nRecorrido en pre orden : ” ) ;
20 abb . recorrePreorden ( ) ;
21
22 System . out . p r i n t l n ( ”n nRecorrido en orden : ” ) ;
23 abb . recorreEnorden () ;
24
25 System . out . p r i n t l n ( ”n nRecorrido en post orden : ” ) ;
26 abb . recorrePostorden () ;
27 System . out . p r i n t l n ( ) ;
28 }
29 }
Ejemplo 7.5: Clase de prueba para el árbol binario de búsqueda
7.2.4. Eliminación
La eliminación de un elemento de un árbol binario de búsqueda, consiste
básicamente en, dado un elemento a eliminar:
Identificar si dicho elemento se encuentra en el ABB3
, si no existe, se
podrı́a regresar un valor que indique dicha situación y dejar el ABB sin
cambios.
Si el elemento existe en el ABB, existen tres posibilidades:
1. Si el elemento está almacenado en un nodo hoja, la eliminación es
directa.
3
Identificación de duplicados.

169. 146 CAPÍTULO 7. ÁRBOLES BINARIOS
2. Si el elemento está almacenado en un nodo con un solo hijo, el
hijo sustituye al padre y se elimina el nodo correspondiente.
3. Si el elemento está almacenado en un nodo con dos hijos, la regla
que se adoptará será la de sustituirlo por el hijo más a la derecha
del subárbol izquierdo4
.
Observe también que con el proceso de eliminación descrito con anterio-
ridad:
1. Se conserva la relación de orden que debe mantener un ABB.
2. Se podrı́a incurrir en un intento de eliminación de un ABB vacı́o5
. Por
lo que serı́a conveniente tener una forma de verificar dicha situación.
En función de lo anterior, el diagrama de clases UML de la Figura 7.4
complementa el de la Figura 7.2. Observe que se han realizado las siguientes
modificaciones en la clase ABB:
1. La incorporación de un atributo privado numérico (n), con la finalidad
de llevar el control del número de elementos insertados en el ABB.
Respecto a la implementación de éste, se debe considerar:
a) Inicializar explı́citamente dicho atributo a cero en el constructor.
b) Proporcionar únicamente el método de tipo get para dicho atri-
buto: obtenN().
2. Adición del método elimina, el cual realiza la eliminación de elemento
si éste existe en el ABB devolviendo true como caso de éxito; en caso
contrario, regresa false. Respecto a la implementación de este método,
se debe considerar:
a) Seguir las reglas de eliminación descritas con anterioridad.
b) Lanzar la excepción ExcepcionEDVacia ante un intento de elimi-
nación de un ABB vacı́o, tal y como lo describe la relación que se
muestra en el diagrama de clases de la Figura 7.4.
3. Incorporación del método estaVacio, el cual regresa true si el ABB
está vacı́o, y false en caso contrario.

170. 7.3. ÁRBOLES BINARIOS BALANCEADOS (AVL) 147
Figura 7.4: Diagrama de clases UML para un árbol binario de búsqueda con
eliminación
La implementación de las clases descritas en la Figura 7.4, ası́ como su
correspondiente clase de prueba, se dejan como ejercicio para el lector.
7.3. Árboles binarios balanceados (AVL)
Existen diferentes tipos y variaciones de árboles binarios, y una de las
más importantes es la de los árboles binarios balanceados, árboles binarios
de búsqueda balanceados, o simplemente, árboles AVL.
7.3.1. Definición y conceptos
Un árbol binario balanceado6
es un ABB en el que las alturas de los
dos subárboles de cada nodo difieren a lo más en 1.
El balance de un nodo en un árbol binario en general, y de un árbol
AVL en particular, se define como la altura de su subárbol izquierdo menos
la altura de su subárbol derecho7
(vea la Expresión 7.1). Por convención, la
altura de un árbol AVL nulo o vacı́o se define como -1.
4
También existe la regla simétrica del hijo más a la izquierda del subárbol derecho,
pero no se utilizará en el texto.
5
Lo cual, desde el punto de vista de la implementación, generarı́a una excepción.
6
También conocidos simplemente como árboles AVL en honor a sus creadores Adelson-
V elski y Landis.
7
También existe la correspondiente definición simétrica: la altura de su subárbol derecho
menos la altura de su subárbol izquierdo; pero en este texto se adoptará la primera.

171. 148 CAPÍTULO 7. ÁRBOLES BINARIOS
|altura(arbolIzquierdo) − altura(arbolDerecho)| 2 (7.1)
Durante el proceso de inserción o eliminación puede ocurrir un desbalance,
es decir, que el valor absoluto de la altura de alguno de los nodos del árbol
AVL sea mayor que 1.
En caso de existir desbalance en alguno de los nodos, es decir, una
condición que incumpla lo establecido por la Expresión 7.1, se tiene que
rebalancear el árbol para que éste siga siendo un árbol AVL válido.
En éste sentido, existen cuatro casos que corrigen el balanceo de un árbol
AVL:
Caso 1 : rotación simple derecha.
Caso 2 : rotación simple izquierda.
Caso 3 : rotación doble izquierda derecha.
Caso 4 : rotación doble derecha izquierda.
A continuación se describen dos de estos cuatro casos, debido a que los
otros dos son simétricos, y pueden derivarse fácilmente a partir de los que se
presentan.
7.3.2. Rotación simple
El primer caso de rebalanceo, la rotación derecha también conocida como
rotación simple, se ilustra en la Figura 7.5.
La Figura 7.5 (a) muestra, hasta antes de la inserción del elemento repre-
sentado por el cuadrado rojo (cuadrado más obscuro), un árbol AVL balan-
ceado. El balance puede determinarse gráficamente por los niveles representa-
dos por lı́neas horizontales punteadas8
. Al insertar el elemento representado
por el cuadrado rojo (cuadrado más obscuro), se presenta un desbalance sobre
el nodo B9
.
Por otro lado, la Figura 7.5 (b) muestra la solución al desbalanceo descrito
en el párrafo anterior. Para visualizarlo mejor, imagine que en la Figura 7.5
(a), en el nodo representado por B existe una polea fija, de tal forma que al
“jalar”z hacia abajo, el subárbol izquierdo de B representado por A sube,
8
El balance para los nodos A y B es 0 y 1 respectivamente.
9
Ahora el balance para los nodos A y B es 1 y 2 respectivamente.

172. 7.3. ÁRBOLES BINARIOS BALANCEADOS (AVL) 149
Figura 7.5: Caso 1: Rotación derecha [Wirth]
mientras que B baja convirtiéndose en el subárbol derecho de A. Note cómo
y pasa de ser subárbol derecho de A, a ser subárbol izquierdo de B.
Para el caso de la rotación izquierda, el proceso es análogo pero de manera
simétrica, al de la rotación derecha.
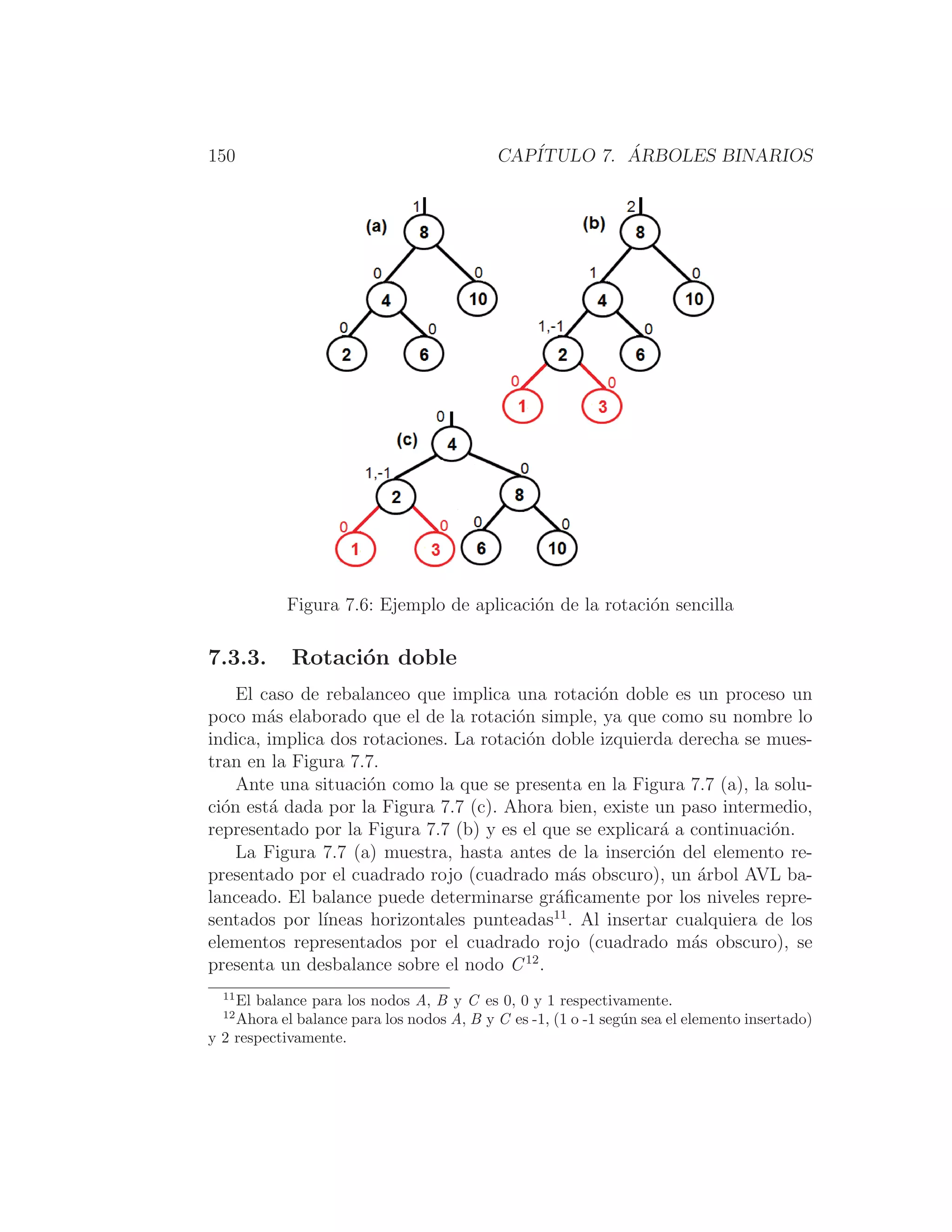
Ejemplo
Considere el árbol AVL que aparece en la Figura 7.6 (a)10
.
La rotación simple derecha se presenta al insertar los elementos 1 o 3, los
cuales se resaltan y presentan en la Figura 7.6 (b).
El nodo desbalanceado es el que contiene al elemento 8 (¿Por qué?). La
aplicación del Caso 1 de rotación, dará como resultado el árbol AVL que
aparece en la Figura 7.6 (c), dependiendo del elemento (1 o 3) que se haya
insertado, de tal forma que la rotación derecha se realiza sobre el nodo que
contiene al elemento 8 de la Figura 7.6 (b).
Observe cómo la aplicación de la rotación simple corrige el balance general
del árbol, de tal forma que el balance obtenido es casi perfecto.
Antes de continuar, asegúrese de comprender el proceso de rebalanceo
aplicado a la Figura 7.6 y de determinar, por su propia cuenta, el balance de
cada uno de los nodos para los tres incisos.
10
Asegúrese de que en efecto sea un árbol AVL, y determine que el balance de cada uno
de los nodos, coincide con el que se presenta fuera de cada nodo.

173. 150 CAPÍTULO 7. ÁRBOLES BINARIOS
Figura 7.6: Ejemplo de aplicación de la rotación sencilla
7.3.3. Rotación doble
El caso de rebalanceo que implica una rotación doble es un proceso un
poco más elaborado que el de la rotación simple, ya que como su nombre lo
indica, implica dos rotaciones. La rotación doble izquierda derecha se mues-
tran en la Figura 7.7.
Ante una situación como la que se presenta en la Figura 7.7 (a), la solu-
ción está dada por la Figura 7.7 (c). Ahora bien, existe un paso intermedio,
representado por la Figura 7.7 (b) y es el que se explicará a continuación.
La Figura 7.7 (a) muestra, hasta antes de la inserción del elemento re-
presentado por el cuadrado rojo (cuadrado más obscuro), un árbol AVL ba-
lanceado. El balance puede determinarse gráficamente por los niveles repre-
sentados por lı́neas horizontales punteadas11
. Al insertar cualquiera de los
elementos representados por el cuadrado rojo (cuadrado más obscuro), se
presenta un desbalance sobre el nodo C12
.
11
El balance para los nodos A, B y C es 0, 0 y 1 respectivamente.
12
Ahora el balance para los nodos A, B y C es -1, (1 o -1 según sea el elemento insertado)
y 2 respectivamente.

174. 7.3. ÁRBOLES BINARIOS BALANCEADOS (AVL) 151
Figura 7.7: Caso 3: Rotación doble izquierda derecha (adaptada de [Wirth])

175. 152 CAPÍTULO 7. ÁRBOLES BINARIOS
Figura 7.8: Ejemplo de aplicación de la rotación doble
Aunque C es el nodo desbalanceado, observe que el balance no se corrige si
se realiza una rotación derecha sobre C (asegúrese de comprobarlo). Por otro
lado, note los signos de los balances generados por la inserción del elemento
que provoca el desbalance.
En base a lo anterior, la Figura 7.7 (b) muestra, aunque A no está des-
balanceado, una rotación izquierda sobre A. Note que el balance no se ha
corregido, ya que el balance de A es 0 o 1, el de B es 2 o 1, y el de C 2.
Ahora bien, partiendo de la Figura 7.7 (b), una nueva rotación derecha
sobre C generará el árbol de la Figura 7.7 (c), mejorando significativamente
el balance general de la mayorı́a de los nodos. Asegúrese de comprender la
doble rotación izquierda derecha explicada hasta aquı́ antes de continuar.
El caso de la rotación doble derecha izquierda es simétricamente análogo.
Ejemplo
Para ilustrar la rotación doble, considere el árbol AVL que aparece en la
Figura 7.8 (a). Una vez más, compruebe que dicho árbol es un árbol AVL y
que los balances propuestos son correctos.

176. 7.4. CONSIDERACIONES FINALES 153
La rotación doble se presenta al insertar cualquiera de los elementos 5 o
7 (Figura 7.8 (b)).
La aplicación de la rotación doble dará como resultado el árbol AVL que
aparece en la Figura 7.8 (c) dependiendo del nodo que se haya insertado. Se
deja como ejercicio para el lector generar el paso intermedio y comparar13
.
Una vez más observe los signos de los balances en la rotación simple y en la
doble; y asegúrese de comprender los procesos de balanceo aplicados en los
ejemplos.
7.4. Consideraciones finales
Los árboles binarios tienen muchas y muy variadas aplicaciones. En este
texto sólo se ha presentado una introducción tanto a los conceptos, como a
algunos de los árboles binarios más comunes, pero es importante que el lector
esté consciente, de que los árboles binarios estudiados en este capı́tulo, no
son los únicos tipos de árboles binarios.
Otro tipos de árboles binarios son, por ejemplo:
Árbol perfectamente balanceado.
Árbol rojo negro.
Árbol AA.
Árbol biselado (splay).
Se recomienda ampliamente al lector buscar información relacionada con
al menos, éste tipo de árboles binarios, con la finalidad de complementar y
ampliar de mejor manera tanto sus conocimientos, como su visión de esta
poderosa y útil estructura de datos.
13
El paso intermedio consiste en hacer una rotación izquierda sobre 4 en la Figura 7.8
(b), y posteriormente una rotación derecha sobre 8. Estas dos rotaciones deberán generar
la Figura 7.8 (c).

177. 154 CAPÍTULO 7. ÁRBOLES BINARIOS
Figura 7.9: Representación de un ABB
7.5. Ejercicios
1. Siguiendo las consideraciones descritas en el texto respecto a un ABB,
realice manualmente, es decir, en papel y lápiz, la inserción de la si-
guiente secuencia de elementos:
14, 15, 4, 9, 7, 18, 3, 5, 16, 4, 20, 17
2. Realice lo mismo que en el ejercicio anterior pero con la secuencia de
números invertida, i.e.:
17, 20, 4, 16, 5, 3, 18, 7, 9, 4, 15, 14
3. Basándose en el Ejemplo 7.1, el Ejemplo 7.2, y el Ejemplo 7.4, realice
las modificaciones correspondientes en ambos tipos de implementación
para que, a través de métodos, proporcione solución a lo siguiente:
a) Dadas dos referencias a dos nodos cualesquiera de un árbol binario,
determine si r1 es padre de r2 (vea la Figura 7.9).
b) Dadas dos referencias a dos nodos cualesquiera de un árbol binario,
determine si r2 es hijo de r1 (vea la Figura 7.9).
c) Dada una referencia a un nodo cualquiera de un árbol binario,
determine si dicho nodo es o no un nodo hoja.
d) Dadas dos referencias a dos nodos cualesquiera de un árbol binario,
determine si r1 es ancestro de r2.

178. 7.5. EJERCICIOS 155
e) Dadas dos referencias a dos nodos cualesquiera de un árbol binario,
determine si r2 es descendiente de r1.
f ) Dada una referencia a un nodo cualquiera de un árbol binario,
determine su nivel.
g) Determinar la altura o profundidad de un árbol binario.
h) Determinar si un árbol binario es o no un árbol estrictamente
binario.
i) Determinar si un árbol binario es o no un árbol binario com-
pleto de profundidad p.
j) La implementación de las operaciones complementarias:
padre: regresa una referencia al padre de nd.
hermano: regresa una referencia al hermano de nd.
esIzquierdo: regresa true si nd es un hijo izquierdo de algún
otro nodo en el árbol binario, y false en caso contrario.
esDerecho: regresa true si nd es un hijo derecho de algún
otro nodo en el árbol binario, y false en caso contrario.
Donde nd es una referencia a un nodo cualquiera de un árbol
binario.
k) Determinar el número de nodos de un árbol binario.
l) La suma14
de todos los nodos del árbol binario.
4. Modifique el Ejemplo 7.3 para que almacene otro tipo de objetos además
de los de la clase Integer. Pruebe con al menos las siguientes clases:
Float.
String.
Persona (del Ejemplo 2.11 del Capı́tulo 2).
Cientifico (del Ejemplo 2.12 del Capı́tulo 2).
5. Realice lo mismo que se pide en el ejercicio anterior, pero para el Ejem-
plo 7.5.
6. Modifique el Ejemplo 7.3 y el Ejemplo 7.5 para que:
14
Se asume que el árbol binario almacena números.

179. 156 CAPÍTULO 7. ÁRBOLES BINARIOS
a) En lugar de insertar números aleatorios en el árbol binario de
búsqueda, solicite al usuario un número de datos n, y después lea
de la entrada estándar cada uno de los n datos, los cuales serán
insertados en el ABB correspondiente.
b) Realice las comprobaciones de los recorridos y árboles generados
manualmente15
.
c) Implemente los recorridos inversos descritos en el texto.
Nota: respecto a los recorridos inversos, resultarı́a sumamente conve-
niente que, previo a la implementación, realizara el diagrama de clases
UML correspondiente, basándose en el de la Figura 7.2.
7. En base a las consideraciones planteadas en el texto respecto a la elimi-
nación de un ABB y al diagrama de clases UML de la Figura 7.4, imple-
mente la eliminación de elementos para un árbol binario de búsqueda,
ası́ como las modificaciones correspondientes mostradas en dicho dia-
grama.
8. Dada la siguiente secuencia de números: 4, 5, 7, 2, 1, 3, 6, genere en
papel y lápiz su correspondiente ABB. Se deberá ilustrar paso a paso
el proceso de inserción, y realizar la comprobación de cada árbol con
el programa generado en el Ejercicio 6.
9. Realice lo mismo que en el ejercicio anterior pero con la secuencia de
números invertida, i.e.: 6, 3, 1, 2, 7, 5, 4.
10. Dada la siguiente secuencia de números: 4, 5, 7, 2, 1, 3, 6, genere en
papel y lápiz su correspondiente árbol AVL. Se deberá ilustrar paso a
paso el proceso de inserción y rebalanceo.
11. Realice lo mismo que en el ejercicio anterior pero con la secuencia de
números invertida, i.e.: 6, 3, 1, 2, 7, 5, 4.
12. Dada la siguiente secuencia de números: 8, 9, 11, 15, 19, 20, 21, 7, 3,
2, 1, 5, 6, 4, 13, 14, 10, 12, 17, 16, 18, generar:
a) El correspondiente ABB.
15
Un recorrido en preorden o postorden, le hará saber si el árbol generado es correcto.
Un recorrido en orden no le arrojará información útil al respecto.

180. 7.5. EJERCICIOS 157
b) El correspondiente árbol AVL.
c) El correspondiente ABB pero con la secuencia de números inver-
tida.
d) El correspondiente árbol AVL pero con la secuencia de números
invertida.
Se deberá ilustrar paso a paso en cada uno de los árboles generados, el
proceso de inserción.
13. Respecto a los cinco ejercicios anteriores:
¿Qué conjeturas puede obtener?
¿En qué tipo de árbol se genera el árbol de altura mı́nima?
¿Cuáles serı́an las ventajas y desventajas de uno y otro esquema
de representación de árbol y por qué?
14. Considere la Figura 7.10 (a), la cual representa un árbol AVL. Utili-
zando papel y lápiz, elimine la siguiente secuencia de elementos:
4, 8, 6, 5, 2, 1, 7
Deberá ilustrar paso a paso:
a) Los balances de cada unos de los nodos.
b) La identificación del nodo a eliminar y el proceso de rebalanceo a
aplicar en caso de ser necesario.
c) El correspondiente árbol AVL.
La solución final al ejercicio se presenta en la Figura 7.10 (b).
15. Genere el diagrama de clases UML que represente el diseño de un árbol
AVL en base a lo expuesto en el texto. Puede basarse en el diagrama
de la Figura 7.4.
La idea de este ejercicio, es que su diseño derive en una implementación.
16. Realice la implementación de un árbol AVL. Tome en consideración
que, además de mantener los elementos ordenados como en un ABB,
en cada inserción deberá verificar el balance de los nodos, y que en caso
de ser necesario, deberá aplicar los mecanismos de rebalanceo descritos
en el texto para asegurar que el árbol generado es siempre, un árbol
AVL.

181. 158 CAPÍTULO 7. ÁRBOLES BINARIOS
(a) AVL (b) Solución
Figura 7.10: Eliminación en un árbol AVL (adaptada de [Wirth])
17. En el texto se discuten los aspectos de los árboles AVL relacionados
con el rebalanceo después de la inserción. Sin embargo, ¿qué pasa con
la eliminación de elementos?
Apoyándose en el texto y en el ejercicio anterior, analice y resuelva
los aspectos implicados en la eliminación de nodos en un árbol AVL,
e implemente una operación que permita realizar la eliminación de un
elemento. Asegúrese de mantener siempre un árbol AVL.

182. Apéndice A
Java
Java and C++ make you think that the new ideas are like the
old ones. Java is the most distressing thing to hit computing
since MS-DOS.
Alan Curtis Kay
El lenguaje de programación Java1
es amado por muchos y odiado por
otros y no participaré en un debate infructuoso. Sólo diré que, como casi
todo en la vida, Java tiene sus ventajas y desventajas, pero lo que es in-
negable, es que es un lenguaje de programación ampliamente difundido y
utilizado, y en ese sentido, resulta importante conocerlo y familiarizarse con
él, independientemente de las posturas ideológicas y preferencias personales.
El presente apartado, no es un tratado del lenguaje, es más, ni siquiera
se acerca a un resumen, es más bien un compendio de referencia a la mano
para el lector familiarizado con algún lenguaje de programación, pero debe
quedar claro que su objetivo no es el de enseñar el lenguaje de programación
Java.
La referencia obligada para este apéndice y para todo el libro en general
es el API (Application Programming Interface) que, al momento de escribir
este libro corresponde a la versión 72
.
1
Java es una marca registrada de Oracle Corporation.
2
http://docs.oracle.com/javase/7/docs/api/
159

183. 160 APÉNDICE A. JAVA
A.1. Orı́genes y caracterı́sticas
Java es un lenguaje de programación originalmente desarrollado por Ja-
mes Gosling cuando trabajaba en la desaparecida empresa Sun Microsystems,
la cual fue adquirida por Oracle Corporation en el año 2009.
El lenguaje fue publicado oficialmente en 1995 y deriva su sintaxis de C y
C++, pero cuenta con menos facilidades de bajo nivel que cualquiera de ellos.
Sin embargo, las aplicaciones o programas de Java son generalmente compi-
ladas a bytecodes, los cuales pueden procesarse en cualquier máquina virtual
Java (JVM) sin importar la arquitectura de la computadora, permitiendo
ası́ una mayor portabilidad del software.
Java es un lenguaje de programación de propósito general, concurrente,
basado en clases, y orientado a objetos, diseñado especı́ficamente para tener
tan pocas dependencias de implementación como fuera posible. Su intención
es permitir que los desarrolladores de aplicaciones escriban el programa una
vez, y lo ejecuten en cualquier dispositivo (WORA, Write Once, Run Anyw-
here).
A.2. Estructura general de una clase
La estructura general de la definición de una clase en Java es como la que
se muestra en el Ejemplo A.1.
Las lı́neas 1-5 muestran el uso de comentarios, se recomienda ampliamente
iniciar la definición de cada clase con un comentario que describa el propósito
de la clase. También es posible definir comentarios de la forma que se muestra
en las lı́neas 10, 13, 17, y 18.
La lı́nea 6 muestra la definición de paquetes. Un paquete es un conjunto de
clases relacionadas, y la palabra reservada package, especifica a qué paquete
pertenecen todas las clases definidas en el archivo fuente.
En Java es posible definir más de una clase por archivo, pero sólo una de
ellas puede ser pública, y su nombre (identificador) debe corresponder con el
nombre del archivo que la contiene. Para el caso del Ejemplo A.1, el nombre
de la clase es EstructuraJava y el del archivo es EstructuraJava.java.
La lı́nea 7 muestra la importación de clases. Las clases se encuentran
ubicadas en paquetes dentro del API, y cuando una clase utiliza alguna clase
definida en algún otro paquete, ésto se especifica con la palabra reservada
import.

184. A.2. ESTRUCTURA GENERAL DE UNA CLASE 161
1 /∗ Estructura general de una c l a s e en Java .
2 Es recomendable i n i c i a r l a d e f i n i c i o n de cada c l a s e con
3 un comentario que describa e l proposito de l a c l a s e .
4 @autor Ricardo Ruiz Rodriguez
5 ∗/
6 package paquete ;
7 import paquete . Clase ;
8
9 public class EstructuraJava {
10 // Definicion del ( l o s ) a t r i b u t o ( s )
11 NombreClase objeto ;
12
13 // Definicion del ( l o s ) constructor ( es )
14 EstructuraJava ( ) {
15 }
16
17 // Definicion del ( l o s ) metodo ( s ) , l o s cuales puede
18 // ser publicos , protegidos o privados
19 public ClaseR metodo ( ) {
20 }
21 }
Ejemplo A.1: Estructura general de una clase en Java
Las clases se definen por medio de la cláusula class y un identificador.
En general, Java define tres niveles de acceso:
1. public (público) hace que una clase, método o atributo sea accesible
por cualquier otra clase.
2. protected (protegido) hace a un método o atributo accesible única-
mente por las clases del mismo paquete, o por subclases de la clase.
3. private (privado) hace a un método o atributo accesible únicamente
desde su propia clase.
La lı́nea 11 muestra la definición de atributos, los cuales están compuestos
por un identificador para el objeto (objeto), y el nombre de la clase de la que
se derivará. La definición de todos los atributos necesarios para la clase,
siguen la misma estructura.
Las lı́neas 14-15 muestran la definición de constructores. En la instancia-
ción, los objetos se construyen, por lo que no es posible crear un nuevo objeto
sin un constructor. Un constructor es el código que se procesa cuando se
crea un objeto a través de la cláusula new. La construcción de un objeto
es un mecanismo mucho más elaborado del que aquı́ se describe, pero la
explicación a detalle queda fuera de los alcances de este apéndice.

185. 162 APÉNDICE A. JAVA
Finalmente, las lı́neas 19-20, muestran la definición de métodos. Los méto-
dos siguen los niveles de acceso descritos con anterioridad, pueden o no regre-
sar un objeto de alguna clase (ClaseR) o un tipo de dato primitivo, y puede
haber tantos, como servicios quiera proporcionar la clase que los define.
En las secciones siguientes se describirán algunos elementos adicionales
del lenguaje.
A.3. Bienvenid@ a Java
El Ejemplo A.2 muestra el primer programa en Java que se discutirá, y
el más simple que es posible hacer.
1 /∗ Ejemplo de Bienvenido a Java ( version 1.0) .
2 @autor Ricardo Ruiz Rodriguez
3 ∗/
4 public class Bienvenido1 {
5 public static void main ( String [ ] args ) {
6 System . out . p r i n t l n ( ”Bienvenid@ a Java ! ” ) ;
7 }
8 }
Ejemplo A.2: Primer programa en Java (versión 1.0)
La lı́nea 5 del Ejemplo A.2, muestra el punto de entrada de cualquier
programa en Java: el método main. Éste método siempre tendrá la forma
que se muestra, la cual se conoce en general como la firma del método. La
explicación y los detalles de args se realizarán en la Sección A.5.4.
En Java sólo es posible enviar mensajes a objetos que definan métodos
públicos; sin embargo, la clase Bienvenido1 del Ejemplo A.2 establece que su
método main es static, lo cual quiere decir que puede ser invocado (llamado)
sin una instancia especı́fica que lo reciba3
.
Finalmente, la forma más común de imprimir mensajes en la salida estándar
(pantalla), es la que aparece en la lı́nea 6 del Ejemplo A.2. System es una cla-
se de servicios que tiene Java, y entre dichos servicios está el método println
del objeto out, el cual recibe como argumento un objeto que representa una
cadena (String), y lo envı́a a la salida estándar imprimiendo un salto de lı́nea
al final4
. La salida del Ejemplo A.2 se muestra en la Figura A.1.
3
De hecho ésto es un mecanismo que utiliza Java para poder generar clases de utilerı́as
o servicios, sin embargo su uso deberı́a ser minimizado, ya que se incurre en el estilo de la
programación estructurada al utilizar dichas clases como bibliotecas de funciones.
4
Para más detalles consulte por favor el API de Java.

186. A.3. BIENVENID@ A JAVA 163
Figura A.1: Salida del Ejemplo A.2
Figura A.2: Salida del Ejemplo A.4
1 /∗ Ejemplo de Bienvenido a Java ( version 1.1) .
2 @autor Ricardo Ruiz Rodriguez
3 ∗/
4 public class Bienvenido2 {
5 public static void main ( String [ ] args ) {
6 System . out . print ( ”Bienvenid@ ” ) ;
7 System . out . p r i n t l n ( ”a Java ! ” ) ;
8 }
9 }
Ejemplo A.3: Primer programa en Java (versión 1.1)
Una versión ligeramente modificada del Ejemplo A.2 se muestra en el
Ejemplo A.3.
Observe que ahora en la lı́nea 6 se ha cambiado el método println por
el método print. Éste último hace lo mismo que el método println, con la
diferencia de que el método print no imprime un salto de lı́nea al final, de
ahı́ que se haya dejado un espacio al final de la cadena Bienvenid@. La salida
del Ejemplo A.3 es idéntica a la que se muestra en la Figura A.1.
1 /∗ Ejemplo de Bienvenido a Java ( version 1.2) .
2 @autor Ricardo Ruiz Rodriguez
3 ∗/
4 public class Bienvenido3 {
5 public static void main ( String [ ] args ) {
6 System . out . p r i n t l n ( ”Bienvenid@nanJava ! ” ) ;
7 }
8 }
Ejemplo A.4: Primer programa en Java (versión 1.2)
Un tercera variación del Ejemplo A.2 se muestra en el Ejemplo A.4, el
cual muestra el uso de la secuencia de escape n para introducir un salto de
lı́nea en cualquier parte de la cadena que se desea imprimir. La salida del
Ejemplo A.4 se muestra en la Figura A.2.

187. 164 APÉNDICE A. JAVA
Finalmente se presenta el Ejemplo A.5, el cual hace uso de la función
printf para imprimir un mensaje en la pantalla. Aquellos lectores que es-
ten familiarizados con el lenguaje de programación C se sentirán cómodos
utilizando dicha función.
1 /∗ Ejemplo de Bienvenido a Java ( version 1.3) .
2 @autor Ricardo Ruiz Rodriguez
3 ∗/
4 public class Bienvenido4 {
5 public static void main ( String [ ] args ) {
6 System . out . p r i n t f ( ” % s n % s n % s n” , ”Bienvenid@” , ”a” , ”Java ! ” ) ;
7 }
8 }
Ejemplo A.5: Primer programa en Java (versión 1.3)
Sin entrar mucho en detalles, sólo se indicará que %s es un especificador
de formato que le indica a la función printf imprima una cadena, misma que
tomará después de la primera coma (,). Es importante señalar que por cada
especificador de formato (tres en el ejemplo) debe existir su correspondiente
cadena. La salida del Ejemplo A.5 es idéntica a la que se muestra en la Figura
A.2.
A.4. Compilación
Existen diferentes entornos de programación o (IDE) que pueden ser utili-
zados para desarrollar programas en Java, como JavaBeans, JCreator, Eclip-
se, etc., se recomienda al lector buscar y familiarizarse con alguno de ellos, o
con algún otro IDE que sea de su preferencia.
Esta sección describe muy brevemente los pasos para la compilación desde
la lı́nea de comandos, ya que los programas de ejemplo de todo el libro,
pueden ser visualizados y editados en cualquier editor de texto, y compilados
con el compilador de Java (javac) sin necesidad de un IDE. Es importante
aclarar que se asume que se tiene instalado el jdk. Si tiene dudas al respecto,
consulte los detalles de instalación del jdk en la página oficial de Java.
Para saber la versión de Java que tiene instalada, puede escribir desde la
lı́nea de comandos:
$ javac -version
Lo que deberá aparecer en su pantalla es la versión correspondiente del
compilador; si aparece un mensaje distinto, es probable que no tenga insta-
lado el jdk o que las rutas de acceso no sean las correctas.

188. A.5. EJEMPLOS SELECTOS 165
Para compilar el programa del Ejemplo A.2, tiene que escribir:
$ javac Bienvenido1.java
Cuando un programa se compila siguiendo la idea planteada, se buscarán
todas las clases requeridas dentro del directorio de trabajo actual, mismo que
corresponde al directorio en donde se haya ejecutado el compilador de Java.
Si alguna clase tuviera algún problema, se reportará dicha situación antes de
volver a visualizar el sı́mbolo del sistema ($); en otro caso, se visualiza de
manera casi inmediata el sı́mbolo del sistema, y observará que se han creado
nuevos archivos, los cuales corresponden a los nombres de las clases pero
con extensión class, mismos que representan los bytecodes que interpreta la
máquina virtual de Java.
La máquina virtual de Java o JVM (Java Virtual Machine) es la encarga-
da de interpretar y procesar los bytecodes que representan las instrucciones
del programa compilado. La JVM está representada por el programa java,
por lo que, para ejecutar un programa en Java, se debe proporcionar a la
JVM la clase principal, la cual es la que contiene el método main:
$ java Bienvenido1
La salida del comando anterior, deberı́a ser el mensaje presentado en la
Figura A.1.
A.5. Ejemplos selectos
Es imposible presentar, ya no digamos en un capı́tulo, sino en un libro
completo un conjunto de ejemplos representativos para cualquier lenguaje
de programación; sin embargo, en esta sección se han seleccionado algunos
ejemplos que pudieran ser de utilidad para la familiarización con el lenguaje
de programación Java, y para comprender los ejemplos desarrollados en el
libro.
A.5.1. Lectura de datos
Una de las tareas más comunes para cualquier programa, es la lectura
de datos desde la entrada estándar (teclado). Para los programas del libro
que utilizan entrada de datos, se sugiere el enfoque que se presenta en el

189. 166 APÉNDICE A. JAVA
Ejemplo A.6, el cual no hace uso de una interfaz gráfica de usuario (GUI) para
mantener la atención en los aspectos relevantes, y también para mantener
más cortos los programas.
El Ejemplo A.6 muestra en la lı́nea 4 la importación de la clase Scanner
del paquete java.util, el cual es un paquete con diversas utilerı́as5
.
Las instancias de la clase Scanner (como entrada) proporcionan diferen-
tes servicios, entre ellos el método nextInt, el cual se encarga de obtener el
siguiente número entero de la entrada estándar (lı́neas 17 y 19).
1 /∗ Ejemplo de l e c t u r a de datos .
2 @autor Ricardo Ruiz Rodriguez
3 ∗/
4 import java . u t i l . Scanner ;
5
6 public class Lectura {
7 public static void main ( String [ ] args ) {
8 // Se crea un o b j e t o ( instancia ) de l a c l a s e Scanner (API)
9 // para obtener ( l e e r ) datos de l a entrada estandar
10 Scanner entrada = new Scanner ( System . in ) ;
11
12 Integer numero1 ;
13 Integer numero2 ;
14 Integer suma ;
15
16 System . out . print ( ”Primer entero ? : ” ) ; // prompt
17 numero1 = entrada . nextInt () ; // l e e un numero entero
18 System . out . print ( ”Segundo entero ? : ” ) ; // prompt
19 numero2 = entrada . nextInt () ; // l e e otro numero entero
20
21 suma = numero1 + numero2 ; // Realiza l a suma
22 // Presenta e l r e s u l t a d o
23 System . out . p r i n t f ( ” % d + % d = % dn” , numero1 , numero2 , suma) ;
24 }
25 }
Ejemplo A.6: Lectura de datos desde la entrada estándar
Observe que el objeto entrada ha sido creado (lı́nea 10) utilizando el
objeto in de la clase System que, por decirlo de una manera simple, es la parte
complementaria de System.out. Éste es el mecanismo usual para la entrada
de datos. También note que han sido declarados tres objetos pertenecientes
a la clase Integer (lı́neas 12-14).
Java también maneja lo que se conoce como tipos de datos primitivos
al estilo de C, la clase Integer es en realidad una envoltura (wrapper) para
el tipo de dato int. Una posible salida para el Ejemplo A.6 se muestra en la
Figura A.3.
5
Se recomienda en este momento echar un vistazo en el API de Java para tener una

190. A.5. EJEMPLOS SELECTOS 167
Figura A.3: Salida del Ejemplo A.6
A.5.2. Estructuras de control
Java incorpora las estructuras de control tradicionales, las cuales se asu-
men conocidas por el lector. Esta sección presenta un resumen incompleto
de las estructuras de control de selección y de repetición, únicamente para
tenerlas como una referencia inmediata.
Estructuras de selección
El Ejemplo A.7 muestra el uso de la estructuras de selección if y los
operadores relacionales (lı́neas 20-31), ası́ como el uso de la estructura de
selección if-else (lı́neas 33-38).
Los lectores familiarizados con el lenguaje de programación C notarán
que tanto las estructuras de selección, como los operadores relacionales son
idénticos en Java, pero a diferencia de C, sı́ existe el tipo booleano, por lo que
en Java es válido decir que una expresión se evalúa como verdadera o falsa
según sea el caso.
Note que las lı́neas 34 y 36 han hecho uso de una expresión de concate-
nación de cadenas de la forma:
objeto + cadena + objeto
lo cual es bastante común en Java, y lo que hace es precisamente conca-
tenar las cadenas por medio del operador +. Note que aunque los objetos,
como en el caso del ejemplo no son cadenas, Java incorpora en la mayorı́a de
sus clases el método toString, el cual se encarga de regresar una representa-
ción de cadena del objeto correspondiente.
De hecho se recomienda que, en la medida de lo posible, las clases definidas
por el usuario definan el método toString con la intención de mantener una
compatibilidad con este tipo de situaciones. Tome en cuenta que aunque el
método toString es heredado de la clase Object (la clase base en Java), es
recomendable definir un comportamiento particular para una clase especı́fica.
Note también que no existe un llamado explı́cito del método, sino un llamado
mejor idea de las clases que contiene el paquete java.util.

191. 168 APÉNDICE A. JAVA
implı́cito, el cual se realiza a través del operador de concatenación de cadenas
+.
1 /∗ Ejemplo de l a estructura de s e l e c c i o n i f y
2 l o s operadores r e l a c i o n a l e s .
3 @autor Ricardo Ruiz Rodriguez
4 ∗/
5 import java . u t i l . Scanner ;
6
7 public class I f {
8 public static void main ( String [ ] args ) {
9 Scanner entrada = new Scanner ( System . in ) ;
10
11 Integer numero1 , numero2 ;
12
13 System . out . print ( ”Primer entero ? : ” ) ;
14 numero1 = entrada . nextInt () ;
15 System . out . print ( ”Segundo entero ? : ” ) ;
16 numero2 = entrada . nextInt () ;
17
18 // Si alguna expresion es verdadera , se procesa l a sentencia
19 // System correspondiente
20 i f ( numero1 == numero2 )
21 System . out . p r i n t f ( ” % d == % dn” , numero1 , numero2 ) ;
22 i f ( numero1 != numero2 )
23 System . out . p r i n t f ( ” % d != % dn” , numero1 , numero2 ) ;
24 i f ( numero1 numero2 )
25 System . out . p r i n t f ( ” % d % dn” , numero1 , numero2 ) ;
26 i f ( numero1 numero2 )
27 System . out . p r i n t f ( ” % d % dn” , numero1 , numero2 ) ;
28 i f ( numero1 = numero2 )
29 System . out . p r i n t f ( ” % d = % dn” , numero1 , numero2 ) ;
30 i f ( numero1 = numero2 )
31 System . out . p r i n t f ( ” % d = % dn” , numero1 , numero2 ) ;
32
33 i f ( numero1 % numero2 == 0)
34 System . out . p r i n t l n ( numero1 + ” es d i v i s i b l e por ” + numero2 ) ;
35 else i f ( numero2 % numero1 == 0)
36 System . out . p r i n t l n ( numero2 + ” es d i v i s i b l e por ” + numero1 ) ;
37 else
38 System . out . p r i n t l n ( ”Los numeros no son d i v i s i b l e s entre s i ” ) ;
39 }
40 }
Ejemplo A.7: Uso de la estructura de selección if y de los operadores
relacionales
Una posible salida para el Ejemplo A.7, se muestra en la Figura A.4. Por
otro lado, la Tabla A.1 muestra la lista de operadores relacionales utilizados
en Java.

192. A.5. EJEMPLOS SELECTOS 169
Figura A.4: Salida del Ejemplo A.7
Operador Descripción
== Igual que
! = Distinto de
Menor estricto que
Mayor estricto que
= Menor igual que
= Mayor igual que
Tabla A.1: Operadores relacionales en Java
Estructuras de repetición
Las estructuras de repetición while, do-while y for se muestran, respec-
tivamente en los Ejemplos A.8, A.9 y A.10.
1 /∗ Ejemplo del c i c l o while .
2 @autor Ricardo Ruiz Rodriguez
3 ∗/
4 public class While{
5 public static void main ( String [ ] args ) {
6 int contador = 1;
7 while ( contador = 10) {
8 System . out . p r i n t f ( ” % d ” , contador ) ;
9 contador++;
10 }
11 System . out . p r i n t l n ( ) ;
12 }
13 }
Ejemplo A.8: Estructura de repetición while
Los Ejemplos A.8, A.9 y A.10 se explican por sı́ mismos. Note que en los
tres ejemplos se ha utilizado el tipo de dato primitivo int para la variable de
control contador.
La salida de los tres ejemplos es la misma, y se muestra en la Figura A.5.

193. 170 APÉNDICE A. JAVA
Figura A.5: Salida de los Ejemplos A.8, A.9 y A.10
1 /∗ Ejemplo del c i c l o do−while .
2 @autor Ricardo Ruiz Rodriguez
3 ∗/
4 public class DoWhile{
5 public static void main ( String [ ] args ) {
6 int contador = 1;
7
8 do{
9 System . out . p r i n t f ( ” % d ” , contador ) ;
10 contador++;
11 }while ( contador = 10) ;
12
13 System . out . p r i n t l n ( ) ;
14 }
15 }
Ejemplo A.9: Estructura de repetición do-while
1 /∗ Ejemplo del c i c l o for .
2 @autor Ricardo Ruiz Rodriguez
3 ∗/
4 public class For{
5 public static void main ( String [ ] args ) {
6 for ( int contador = 1; contador = 10; contador++)
7 System . out . p r i n t f ( ” % d ” , contador ) ;
8 System . out . p r i n t l n ( ) ;
9 }
10 }
Ejemplo A.10: Estructura de repetición for
A.5.3. Arreglos
El Ejemplo A.11 muestra la creación, recorrido e impresión de un arreglo
de enteros (int).
La lı́nea 7 define al objeto arreglo como un arreglo de enteros. Observe
que el objeto es creado (new), con un tamaño especı́fico (diez).
Adicionalmente se definen también un par de variables:
1. Un valor inicial: valor (lı́nea 8).
2. Un incremento: incremento (lı́nea 9)

194. A.5. EJEMPLOS SELECTOS 171
Figura A.6: Salida del Ejemplo A.11
Los arreglos en Java, al ser creados y definidos como objetos, tienen de-
finido el atributo público length, el cual almacena la longitud del arreglo.
Dicha propiedad es la que se utiliza como expresión condicional en los ciclos
for de las lı́neas 12 y 17 respectivamente.
1 /∗ Ejemplo de a r r e g l o s .
2 @autor Ricardo Ruiz Rodriguez
3 ∗/
4 public class Arreglo {
5 public static void main ( String [ ] args ) {
6 // Se define un arreglo de diez enteros
7 int [ ] a r r e g l o = new int [ 1 0 ] ;
8 int valor = 1974;
9 int incremento = 22;
10
11 // Se i n i c i a l i z a e l a rr e g lo
12 for ( int i = 0; i a r r e g l o . length ; i++)
13 a r r e g l o [ i ] = valor + incremento ∗ i ;
14
15 // Se imprime e l a rr e g lo
16 System . out . p r i n t l n ( ” Valores generados y almacenados en e l a r r e g l o : ” ) ;
17 for ( int i = 0; i a r r e g l o . length ; i++)
18 System . out . print ( a r r e g l o [ i ] + ” ” ) ;
19 System . out . p r i n t l n ( ) ;
20 }
21 }
Ejemplo A.11: Arreglo de enteros (int)
El primer ciclo recorre el arreglo para inicializar y asignar los valores al
arreglo en función de valor, incremento y la variable de control i.
Por otro lado, el segundo ciclo realiza un recorrido tradicional para im-
presión en la salida estándar. La salida del Ejemplo A.11 se muestra en la
Figura A.6.
A.5.4. Argumentos en la lı́nea de comandos
El Ejemplo A.12 muestra la forma de procesar los argumentos en la invo-
cación de un programa, lo cual resultará útil y necesario en diversas ocasiones,
y para algunos de los ejercicios planteados en el libro.
El objeto args es un arreglo de cadenas (lı́nea 6), por lo que en la lı́nea 7
se verifica si se han proporcionado o no argumentos en la lı́nea de comandos;

195. 172 APÉNDICE A. JAVA
Figura A.7: Salida del Ejemplo A.12 sin argumentos
Figura A.8: Salida del Ejemplo A.12 con argumentos
en caso de que no, se reporta en la lı́nea 8 (Figura A.7), en caso de que sı́,
se procesa la lista de argumentos con un ciclo (lı́nea 10), y se imprime en
la salida estándar, la lista de argumentos proporcionados, mismos que están
almacenados en el arreglo de cadenas args (Figura A.8).
1 /∗ Ejemplo de uso de procesamiento de argumentos en l a l i n e a
2 de comandos a traves del o b j e t o args .
3 @autor Ricardo Ruiz Rodriguez
4 ∗/
5 public class MainArgs{
6 public static void main ( String [ ] args ) {
7 i f ( args . length 1)
8 System . out . p r i n t l n ( ”No hay argumentos para procesar ” ) ;
9 else
10 for ( int i = 0; i args . length ; i++)
11 System . out . p r i n t f ( ”Argumento[ % d ] = % s n” , i , args [ i ] ) ;
12 }
13 }
Ejemplo A.12: Procesamiento de argumentos en la lı́nea de comandos
A.5.5. Excepciones
Las excepciones permiten una abstracción sobre el mecanismo de manejo
de errores ligeros o condiciones que un programa pudiera estar interesado en
atrapar y procesar.

196. A.5. EJEMPLOS SELECTOS 173
Figura A.9: Relación UML de la jerarquı́a de la clases Exception en Java
La idea subyacente en las excepciones es separar el manejo de éste tipo de
condiciones o errores, de la lógica de funcionamiento subyacente al programa.
Una excepción es una situación anormal en la lógica de ejecución esperada
por un programa, como el intentar clonar un objeto que no tiene implemen-
tado el mecanismo de clonación por ejemplo, manejar un formato de datos
inadecuado para algún especificador, intentar realizar una operación de E/S
en un canal cerrado, intentar acceder a elementos de una estructura de datos
que no contiene elementos, entre muchı́simas otras más.
En la práctica, es posible definir en Java clases que gestionen excepciones
o errores de una aplicación en particular. De hecho, una de las intenciones
de las excepciones es la de, ante una problemática determinada, tratar de
solucionarla en la medida de lo posible para continuar con el programa o
aplicación activos, y no la de terminar con la primera dificultad que se pre-
sente.
Un manejo completo y robusto de excepciones es una labor que, si bien
su dominio no requiere de lustros, no es una tarea trivial y queda fuera de
los alcances de este texto.
Para los ejemplos desarrollados en el libro, se hará uso de la excepción
definida por la clase RuntimeException del API, la cual maneja el conjunto

197. 174 APÉNDICE A. JAVA
de excepciones generadas durante la ejecución.
La clase Throwable es la clase base de todas las excepciones que pueden ser
lanzadas en Java, por lo que la revisión de esta jerarquı́a de clases del API, es
un punto inicial fundamental tanto para la comprensión de las excepciones,
como para su referencia permanente. La relación de la jerarquı́a de clases en
la que se encuentra la clase Exception en el contexto de Java, se expresa en
un diagrama de clases de UML (Unified Modeling Language) de la Figura
A.9.
Por otro lado, el Ejemplo A.13 muestra la definición de una excepción
bastante sencilla pero útil, de hecho, la clase mostrada en dicho ejemplo, es
la que se utiliza para las estructuras de datos desarrolladas en el libro.
1 /∗ Ejemplo de d e f i n i c i o n de excepcion .
2 La excepcion sera lanzada cuando se haga un intento de eliminacion
3 de una estructura de datos que e s t e vacia .
4 La c l a s e RuntimeException es l a super c l a s e de l a s excepciones
5 que pueden ser lanzadas durante l a operacion normal de l a JVM.
6 @autor Ricardo Ruiz Rodriguez
7 ∗/
8 public class ExcepcionEDVacia extends RuntimeException{
9 public ExcepcionEDVacia () {
10 this ( ” Estructura de datos ” ) ;
11 }
12
13 public ExcepcionEDVacia ( String s ) {
14 super ( s + ” vacia ” ) ;
15 }
16 }
Ejemplo A.13: Definición de una excepción
Note que la excepción ExcepcionEDVaciaAP es una subclase de la cla-
se RuntimeException. La clase RuntimeException es la super clase de las
excepciones que pueden ser lanzadas durante la ejecución de la JVM.
A.5.6. Genéricos
La definición de jdk 5.0 introdujo nuevas modificaciones y extensiones a
Java, y una de ellas fue el aspecto relacionado con los genéricos (generics).
Los genéricos son en sı́ mismos todo un tema de estudio, pero dado que
se utilizan en la mayorı́a de los ejemplos del libro respecto a la definición de
las estructuras de datos, aquı́ se presenta una exageradamente breve intro-
ducción.
Los genéricos permiten una abstracción sobre los tipos de datos o los
objetos que se procesan, y dentro de sus objetivos se encuentran el eliminar

198. A.5. EJEMPLOS SELECTOS 175
la ambigüedad latente que existı́a en la conversión forzada de tipos (cast) y
la molestia de su realización, ya que usualmente un programador sabe cual
es el tipo de dato que está procesando cuando utiliza una colección de datos
por ejemplo.
El siguiente fragmento de código, se utilizaba antes de los genéricos:
List lista = new LinkedList();
lista.add(Genericos en Java);
String cadena = (String) lista.get(0);
Con los genéricos el programador pone una marca (clase o tipo de da-
tos en particular), por decirlo de alguna manera, para restringir los datos a
almacenar y recuperar:
ListString lista = new LinkedListString();
lista.add(Genericos en Java);
String cadena = lista.get(0);
El cambio es aparentemente simple pero significativo, ya que evita los
errores intencionales o accidentales en tiempo de ejecución, además de que
permite al compilador hacer una verificación sobre los tipos de datos que
se gestionan. Note que en el segundo fragmento de código, el cast ha sido
eliminado.
El Ejemplo A.14 del Ejercicio 10 muestra el uso de genéricos en el contexto
de colecciones (ArrayList). Es ampliamente recomendable para el lector pro-
fundizar más sobre el tema de genéricos, ya que es una de las caracterı́sticas
de Java más ampliamente difundidas.

199. 176 APÉNDICE A. JAVA
Operador Descripción
/ División (cociente)
% Módulo (residuo)
* Multiplicación
+ Adición
- Sustracción
Tabla A.2: Operadores aritméticos en Java
A.6. Ejercicios
1. Investigue más acerca del concepto de máquina virtual y de los byteco-
des. ¿Fue Java el primer lenguaje de programación en incorporar dichos
conceptos?
2. Para el programa del Ejemplo A.3, pruebe lo que sucede si elimina el
espacio que aparece al final de la cadena Bienvenid@. No olvide volver
a compilar.
3. Considere el Ejemplo A.4 e investigue qué otras secuencias de escape
existen, también infórmese si dichas secuencias coinciden o no con las
que se utilizan en el lenguaje de programación C.
4. En base a lo expuesto para el Ejemplo A.5, investigue qué otros especifi-
cadores de formato existen. Infórmese también si dichos especificadores
coinciden o no con los que se utilizan en el lenguaje de programación
C.
5. Utilice el Ejemplo A.6, y cambie la clase Integer por el tipo primitivo
int. Compruebe si es necesario o no hacer algún otro tipo de cambio
para que el programa funcione.
6. En base a lo descrito en el Ejemplo A.6, modifique dicho ejemplo para
agregar las cuatro operaciones aritméticas: suma, resta multiplicación
y división. Los operadores aritméticos se muestran en la Tabla A.2.
Realice también lo anterior para números enteros representados como
objetos (Integer), y como tipos de datos primitivos.

200. A.6. EJERCICIOS 177
7. Modifique el Ejemplo A.6 para procesar ahora números Float y Double.
Tome en cuenta que deberá consultar el API para cambiar el método
nextInt por el método apropiado. Investigue también si existen los tipos
de datos primitivos correspondientes (float y double).
8. Modifique el Ejemplo A.11 para que, utilizando el procesamiento de
argumentos en la lı́nea de comandos como el que se hizo en el Ejemplo
A.12, acepte tres argumentos:
a) Tamaño del arreglo (n).
b) Valor inicial (valor).
c) Incremento (incremento).
Su programa deberá generar un arreglo de n enteros, con un valor
inicial para el primer elemento y un incremento para los demás.
Observe que los elementos de args son cadenas, por lo que tendrá que
consultar el API para utilizar métodos de conversión de cadenas a
números enteros.
Sugerencia: consulte el método parseInt de la clase Integer.
9. Consulte bibliografı́a y la internet para documentarse más acerca del
uso y definición de excepciones en Java.
10. Considere el Ejemplo A.14. Investigue en el API las colecciones, par-
ticularmente la colección ArrayList, y determine el funcionamiento del
programa antes de compilarlo y ejecutarlo en la máquina virtual de
Java.
1 /∗ Ejemplo de una coleccion ArrayList de cadenas .
2 @autor Ricardo Ruiz Rodriguez
3 ∗/
4 import java . u t i l . ArrayList ;
5
6 public class Coleccion {
7 public static void main ( String [ ] args ) {
8 // Con cuantos elementos se crea originalmente e l o b j e t o
cadenas?
9 ArrayListString cadenas = new ArrayListString () ;
10
11 cadenas . add ( ”Java” ) ;
12 cadenas . add (0 , ”C++” ) ;
13
14 System . out . p r i n t l n ( ”Contenido del ArrayList cadenas : ” ) ;
15 imprime ( cadenas ) ;

201. 178 APÉNDICE A. JAVA
16
17 cadenas . add ( ” Smalltalk ” ) ;
18 cadenas . add ( ”Java” ) ;
19 cadenas . add ( ” ObjectiveC ” ) ;
20 System . out . p r i n t l n ( ”Contenido del ArrayList cadenas : ” ) ;
21 imprime ( cadenas ) ;
22
23 cadenas . remove ( ”Java” ) ;
24 System . out . p r i n t l n ( ”Contenido del ArrayList cadenas : ” ) ;
25 imprime ( cadenas ) ;
26
27 cadenas . remove (1) ;
28 System . out . p r i n t l n ( ”Contenido del ArrayList cadenas : ” ) ;
29 imprime ( cadenas ) ;
30
31 System . out . p r i n t f ( ””Java” % s e s t a en e l ArrayList n” ,
cadenas . contains ( ”Java” ) ? ”” : ”no ” ) ;
32 System . out . p r i n t l n ( ”Hay ” + cadenas . s i z e ( ) + ” elementos en e l
ArrayList cadenas ” ) ;
33 }
34
35 // Presenta l o s elementos del ArrayList cadenas en la s a l i d a
estandar
36 public static void imprime ( ArrayListString cadenas ) {
37 for ( String elemento : cadenas )
38 System . out . print ( elemento + ” ” ) ;
39 System . out . p r i n t l n ( ) ;
40 }
41 }
Ejemplo A.14: Uso de una colección ArrayList
Compruebe la deducción del funcionamiento con la salida real del pro-
grama.

202. Bibliografı́a
[Budd] Budd, Timothy A., “An Introduction to Object-Oriented Program-
ming”, Third Edition, Addison Wesley.
[Bracha] Bracha, Gilad, “Generics”, Oracle Corporation,
http://docs.oracle.com/javase/tutorial/extra/generics/ (Julio 2013).
[Deitel] Deitel, H. M. y Deitel, P. J., “Cómo Programar en Java”, Prentice
Hall.
[Kuhn] Kuhn, Thomas Samuel., “The Structure of Scientific Revolutions”,
University of Chicago Press.
[Langsam] Langsam, Yedidyah, Augenstein, M. J. and Tenenbaum, A. M.,
“Estructuras de Datos con C y C++”, Segunda Edición, Prentice Hall
Hispanoamericana.
[Mark] Mark Allen Weiss, “Estructuras de Datos en Java”, Addison Wesley.
[McConnell] McConnell, Steve, “Code Complete”, Second Edition, Micro-
soft.
[Ruiz] Ruiz-Rodrı́guez, Ricardo, “Una Introducción a la Programación Es-
tructurada en C”, El Cid Editor.
[Shalloway] Shalloway, Alan and Trott James R., “Design Patterns Explained
A New Perspective on Object Oriented Design”, Addison Wesley.
[Sierra] Sierra, Kathy and Bates, Bert, “Sun Certified Programmer Deve-
loper for Java 2”, Mc Graw Hill/Osborne.
[Wirth] Wirth, Niklaus, “Algoritmos y Estructuras de Datos”, Prentice Hall.
179

203. 180 BIBLIOGRAFÍA

204. Índice Analı́tico
árbol binario, 129
altura, 131
ancestro, 130
balanceado (AVL), 147
completo, 131
de búsqueda, 135
descendiente, 130
estrictamente binario, 131
hijo, 130
nivel, 130
nodo, 129
nodo hoja, 130
operaciones primitivas, 131
padre, 130
profundidad, 131
raı́z, 129
recorridos, 130, 132
en orden, 133, 136
en orden inverso, 134
inversos, 133, 156
orden posterior, 133, 136
orden posterior inverso, 134
orden previo, 133, 135
orden previo inverso, 133
subárbol derecho, 129
subárbol izquierdo, 129
visitar, 132
Abstract Data Type, 41
Application Programming Interface, 159
Java Virtual Machine, 165
RuntimeException, 44, 174
Throwable, 174
Unified Modeling Language, 25, 174
Write Once Run Anywhere, 160
bytecodes, 160, 165, 176
cast, 175
information hiding, 11
overload, 21, 23
override, 7, 27, 31
wrapper, 166
abstracción, 2, 4, 6, 8, 10, 33, 42
ADT, 50
de datos, 41
excepciones, 172
genéricos, 174
acoplamiento, 9
ADT, 41, 95
complejo, 54
definición del operador, 42
definición del valor, 42
racional, 44
agentes, 4
Alan Kay, 9, 13
algoritmo, 4
API, 73, 74, 159, 160, 174
ArrayList, 175, 177
Comparable, 89
Double, 177
Float, 177
181

205. 182 ÍNDICE ANALÍTICO
Integer, 166, 176, 177
Object, 46
Random, 141, 144
RuntimeException, 73, 173
Scanner, 166
String, 18
System, 162, 166
args, 162, 171
argumentos, 18
arreglo
args, 172
atributos, 5, 7, 19
autorreferencia, 48
C, 41, 160, 164, 166, 176
C++, 13, 41, 160
C#, 41
cadenas
concatenación, 167
cláusula
class, 161
extends, 29
implements, 91
import, 160
interface, 89
new, 17, 21, 161, 170
super, 29, 60
this, 45, 46
throws, 59
throw, 44
try-catch-finally, 62, 74, 85
package, 160
clase, 6, 10
Object, 46, 167
abstracta, 7
atributos, 19
autorreferida, 48
base, 8, 174
de prueba, 16
definición, 10, 161
derivada, 6
hija, 6
importación, 160
jerarquı́a, 7, 10
padre, 6, 89
principal, 165
subclase, 6, 174
super clase, 8, 174
cohesión, 9, 34
cola de espera, 79
peek, 97
de prioridad, 86
fin, 79
inicio, 79
operaciones primitivas, 80
representación, 81
colección, 175, 177
comportamiento, 10, 17
constructor, 21, 44, 161
base, 45
sobrecarga, 46
conversión forzada, 175
do-while, 169
Eiffel, 13
encapsulamiento, 11, 34
enfoque estructurado, 2, 4, 5, 8
entidades, 4, 5
envoltura, 166
especificador de formato, 164, 176
excepción, 173
RuntimeException, 174
ExcepcionEDVacia, 59, 60, 62, 85,
146
lanzar una (throw), 44

206. ÍNDICE ANALÍTICO 183
FIFO, 79
for, 169
funciones, 4
genéricos (generics), 63, 174
GUI, 13, 166
herencia, 8, 10, 11, 25, 89
extends, 29
abstracción, 25, 110
múltiple, 89
IDE, 164
identificador, 160
if, 167
if-else, 167
instancia, 6, 7, 10, 16, 17
interfaz, 5, 19
gráfica, 166
Java, 15, 21, 33, 41, 160
recolector de basura, 60
java, 165
javac, 164
jdk, 164, 174
jerarquı́a, 11
Exception, 174
de clases, 7
JVM, 160, 165, 174
java, 165
recolector de basura, 60
Kuhn Thomas, 3
LIFO, 55
lista, 103
circular, 118
doblemente enlazada, 120
primitivas, 120
enlazada, 103
ordenada, 104
operaciones primitivas, 104
representación, 105
simplemente enlazadas, 117
máquina virtual, 165, 176
métodos, 4, 7, 16
get, 20, 33, 36
nextInt, 166, 177
parseInt, 177
printf, 164
println, 162
print, 163
set, 19, 31, 33, 36
toString, 46, 167
argumentos, 18
definición, 162
firma de, 162
lanzar excepciones (throws), 59
llamado explı́cito, 167
llamado implı́cito, 168
privado, 75, 77
sobre escritura (override), 31
módulo, 8, 9
main, 17, 162, 165
mensajes, 4, 5, 16
modularidad, 8, 10
número racional, 43
niveles de acceso, 26, 33, 161
público (public), 19, 161
privado (private), 19, 161
protegido (protected), 83, 161
nodo, 48
notación
interfija, 69
postfija, 69
prefija, 69

207. 184 ÍNDICE ANALÍTICO
null, 21, 36, 49
objetos, 4, 5, 33
acciones, 10
clase, 4, 10
comportamiento, 10, 17
construcción, 17, 21, 161
creación, 17, 21, 161
definición, 17
identificador, 5
instancia, 10
interfaz, 19
memoria, 10
mensajes, 4, 10
personalidad, 33
protocolo, 6
responsabilidades, 4, 17
rol, 4
servicio, 4
solicitud, 10
ocultación
principio de, 11, 19, 33
OO, 1, 5, 6, 12
operadores
aritméticos, 176
punto, 35, 46
relacionales, 168
Oracle, 160
orientado a objetos, 1, 33, 42
paradigma, 2, 4, 12, 33
programación, 1, 42
público, 19, 161
paquete, 160
paradigma, 2–4
de programación, 3
definición, 2, 3
orientado a objetos, 4
pila, 55, 110
peek, 56, 74
pop, 56, 110
push, 56, 110
primitiva, 57
primitivas, 56
tope, 55
polimorfismo, 11, 21, 23, 31
POO, 1, 9, 42
caracterı́sticas fundamentales, 9
privado, 19, 161
procedimientos, 4
programación
entorno de, 164
estructurada, 5, 8, 162
orientada a objetos, 9, 13, 42
nociones, 50
protegido, 161
referencia, 40, 48, 49, 64
relación
de asociación, 73
de composición, 73, 110
de orden, 88
es un (is-a), 8, 27
tiene (has-a), 8
responsabilidades, 4, 17
rotación
derecha, 148
derecha izquierda, 152
doble, 150
izquierda, 149
izquierda derecha, 150
simple, 148
servicios, 4
clases de, 162
Simula, 1

208. ÍNDICE ANALÍTICO 185
Smalltalk, 1, 13
sobre escribe, 7, 27, 31
sobrecarga, 21, 23
operadores, 33
software
crisis, 1
portabilidad, 160
subclase, 6, 174
Sun Microsystems, 160
super clase, 8, 174
Thomas Kuhn, 3
tipo de dato, 40, 41, 166
double, 52, 177
float, 52, 177
int, 52, 166, 169, 170
abstracto, 41
booleano, 167
genéricos, 175
primitivo, 166, 169, 176, 177
UML, 25, 73, 81, 105, 174
while, 169
WORA, 160
Xerox, 1, 13

209. 186 ÍNDICE ANALÍTICO

210. Agradecimientos
Antes y primero que nada y nadie, quiero agradecer a mis hijos Ricardo
y Bruno, quienes al momento de escribir esto cuentan con seis y cinco años
respectivamente, ya que con sus ocurrencias, sus acciones, su inocencia y su
motivación implı́cita, hacen que la vida y mi esfuerzo valgan la pena.
Quiero renovar también el agradecimiento a mis padres Marı́a Luisa
Rodrı́guez y Rodolfo Ruiz por su educación y formación. Especialmente quie-
ro agradecer a mi madre por apoyarme siempre e incondicionalmente cuando
más lo he necesitado, sobre todo en un trance especial de mi vida; siempre
ha sido, es, y será, la mujer que más ame y añore...
Aprovecho también para agradecer especialmente a Thelma su invaluable
ayuda para la realización de imágenes, el diseño de portada, la revisión del
texto, trámites, y mil cosas más; pero sobre todo por estar conmigo en los
momentos cruciales que ella conoce.
Agradezco el apoyo y la confianza de mi hermano Rodolfo, quien jugó un
papel fundamental para que yo pudiera realizar mis estudios de posgrado.
No sólo tienes mi agradecimiento, reconocimiento y admiración, sino también
una profunda estimación y aprecio.
Para mis amigos Tomás Balderas Contreras y Ricardo Pérez-Aguila, mi
reconocimiento profesional y mi agradecimiento por sus comentarios y suge-
rencias.
Finalmente, agradezco también a todos los estudiantes que me ayudaron
implı́citamente con sus comentarios, preguntas, dudas y observaciones. Este
libro es, sin duda alguna, resultado también de sus aportaciones.
187

211. 188 AGRADECIMIENTOS

212. Acerca del Autor
Ricardo Ruiz Rodrı́guez nació en la
ciudad de Puebla, Pue., México. Ac-
tualmente y desde el año 2002, es pro-
fesor investigador adscrito al Instituto
de Computación en la Universidad Tec-
nológica de la Mixteca (UTM), en Hua-
juapan de León, Oaxaca, México, y cuen-
ta con más de 15 años de experiencia co-
mo docente.
El maestro Ricardo además de la do-
cencia, se ha desempeñado también co-
mo desarrollador de software en la indus-
tria, y se certificó como PSP Developer
en 2013, mismo año en el que publicó su
primer libro ”Una Introducción a la Pro-
gramación Estructurada en C”.
Entre sus intereses actuales se encuentran los métodos de enseñanza de
las ciencias de la computación, la música, y la música por computadora, pero
se ha desarrollado académicamente en áreas como la Ingenierı́a de Software,
la Interacción Humano-Computadora, y el Paradigma Orientado a Objetos.
El autor tiene la Licenciatura en Ciencias de la Computación por la Be-
nemérita Universidad Autónoma de Puebla (BUAP) y la Maestrı́a en Cien-
cias con especialidad en Ingenierı́a en Sistemas Computacionales, por la Uni-
versidad de las Américas-Puebla (UDLA-P).
Información adicional del autor, ası́ como el material relacionado con este
libro y el anterior, se pueden consultar en su página personal:
http://sites.google.com/site/ricardoruizrodriguez/
189