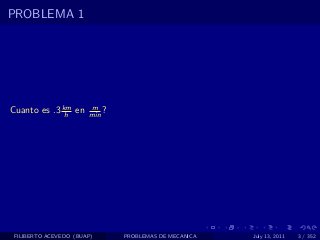
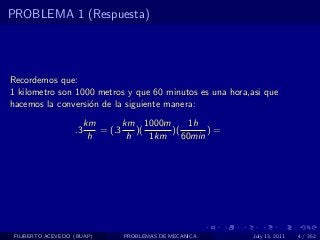
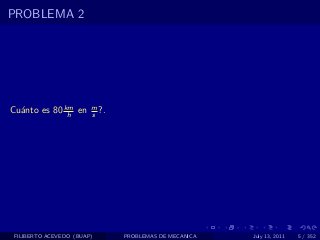
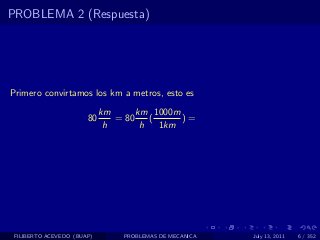
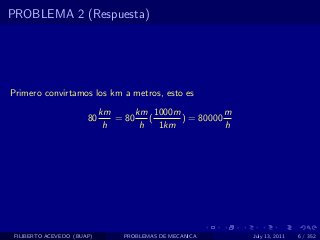
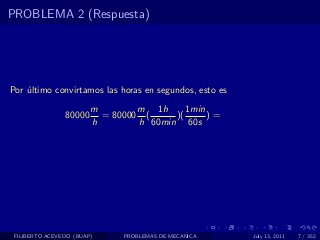
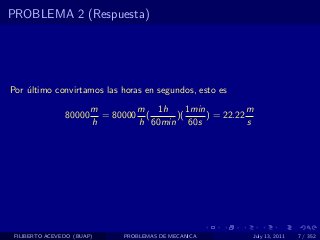
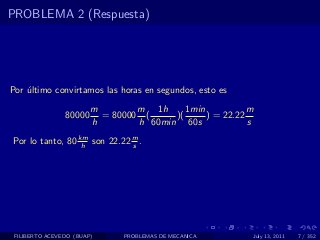
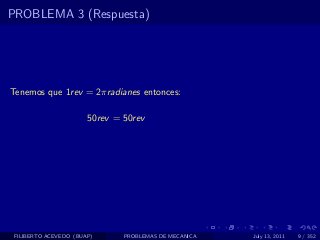
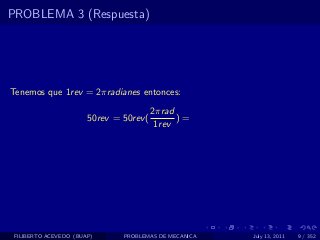
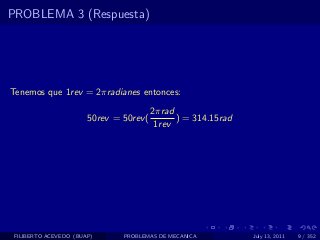
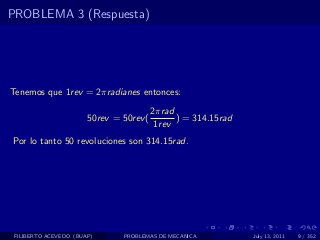
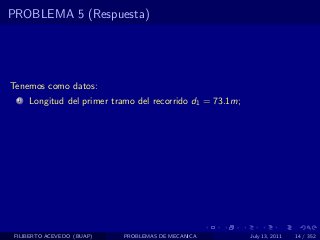
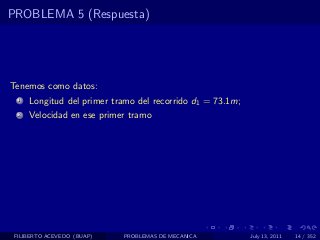
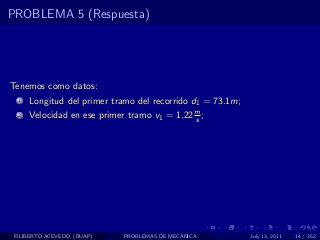
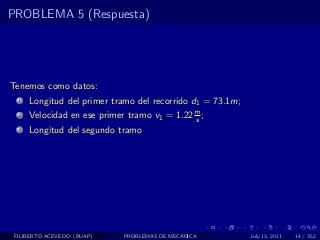
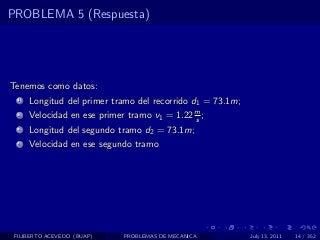
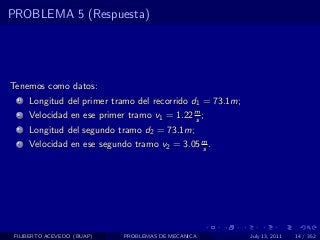
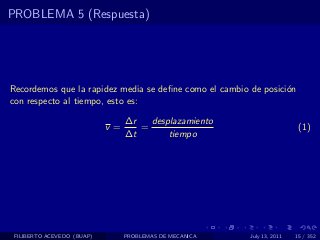
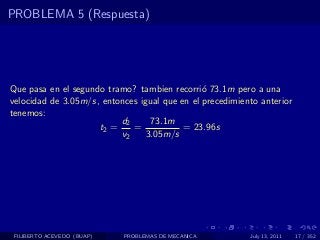
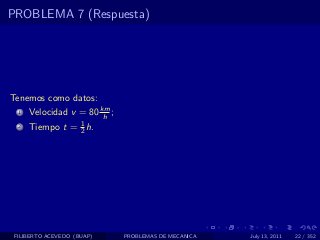
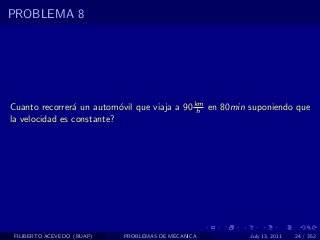
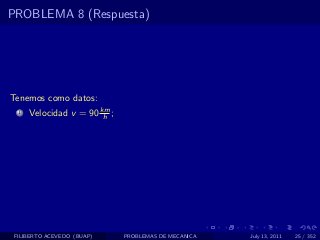
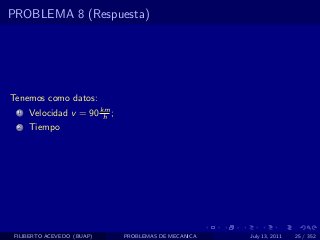
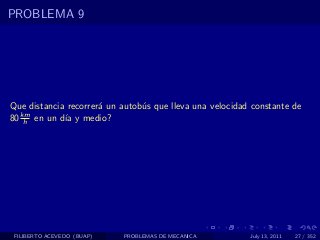
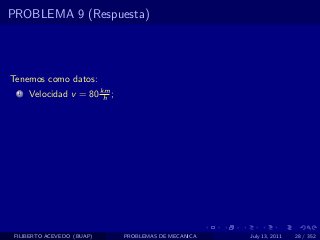
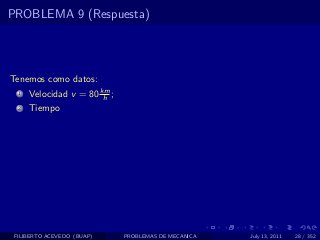
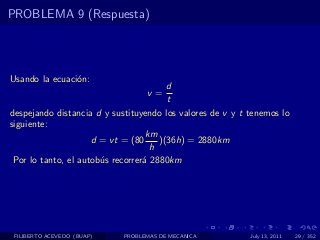
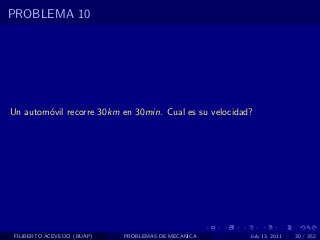
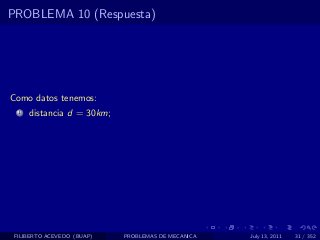
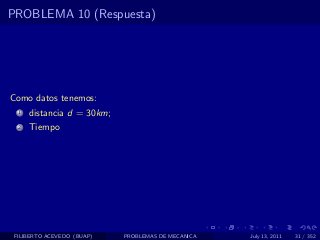
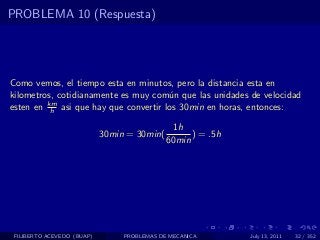
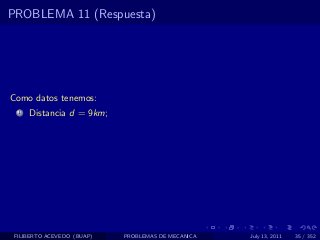
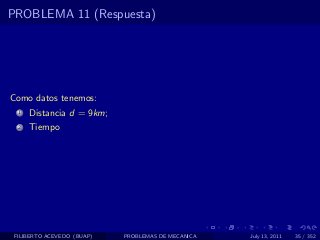
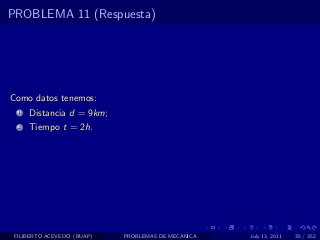
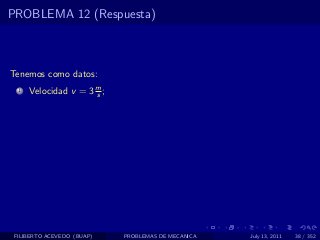
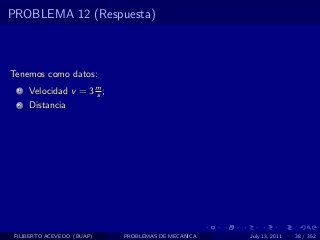
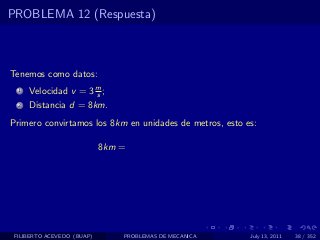
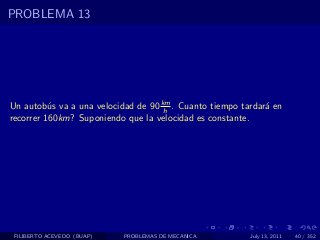
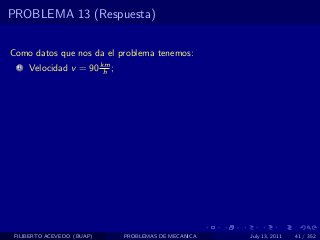
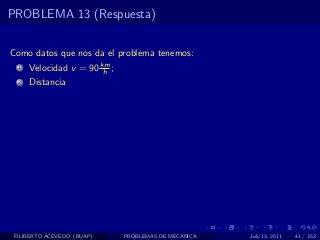
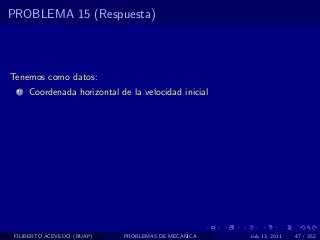
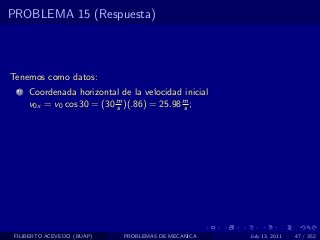
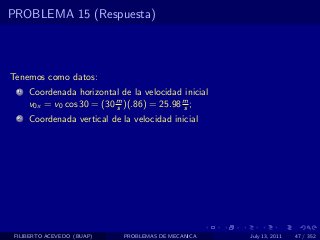
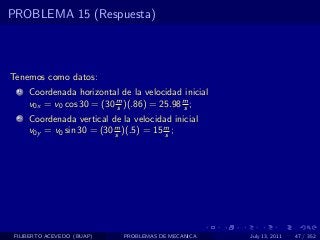
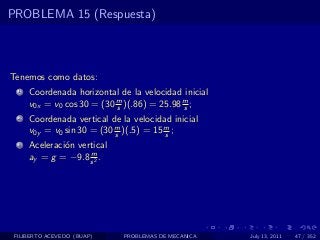
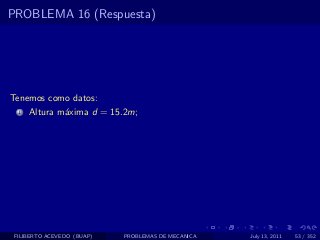
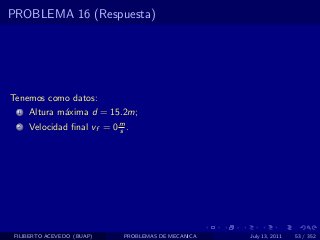
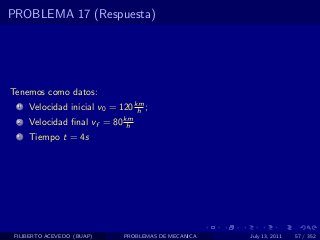
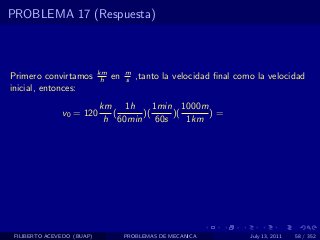
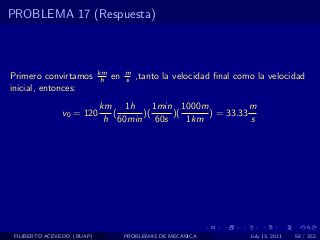
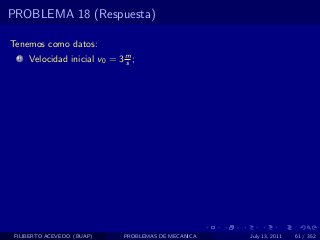
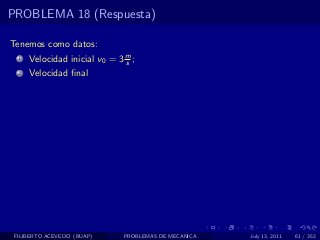
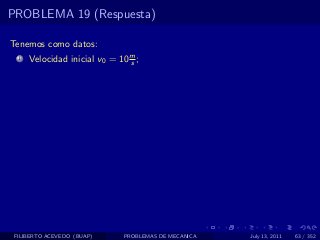
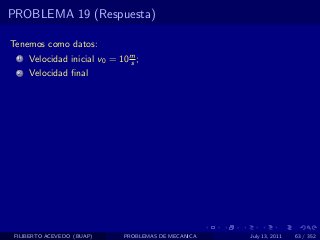
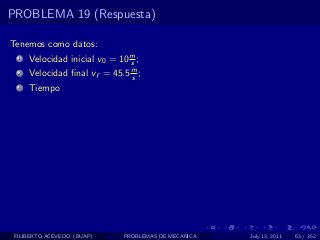
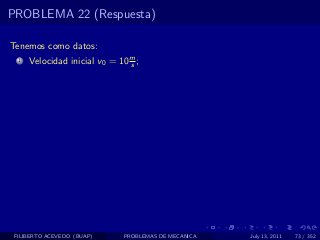
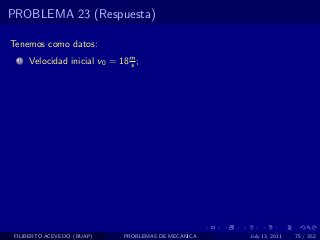
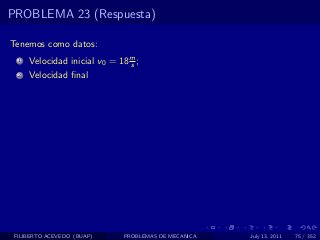
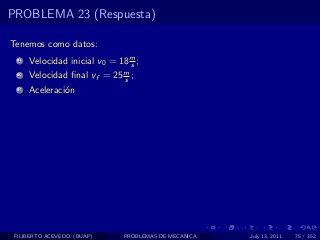
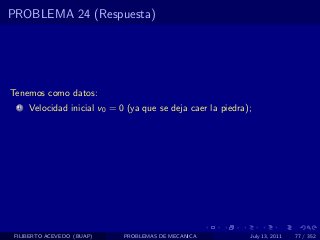
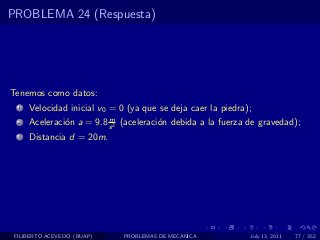
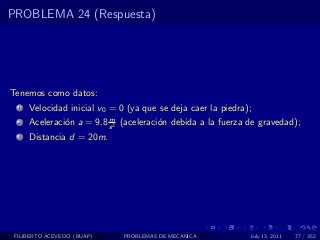
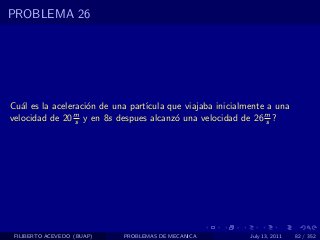
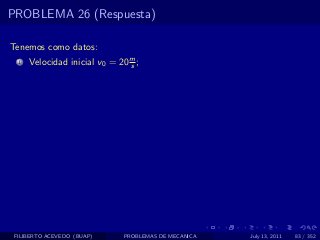
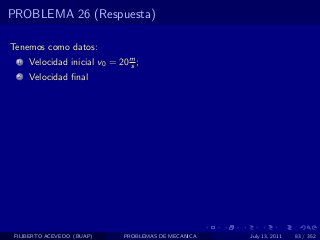
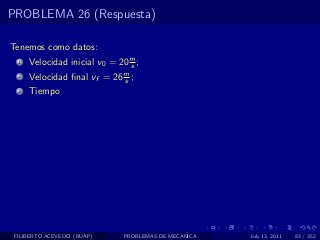
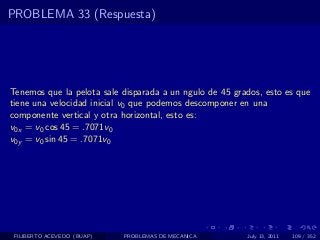
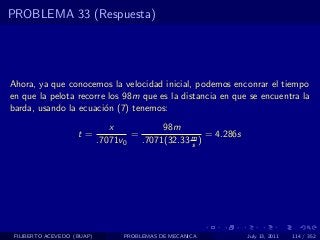
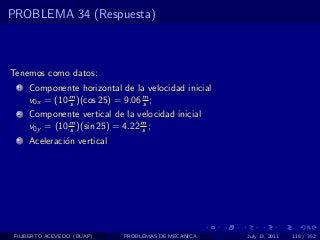
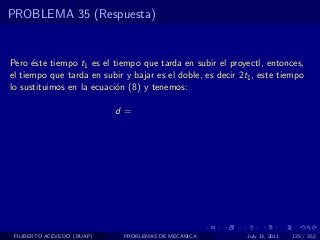
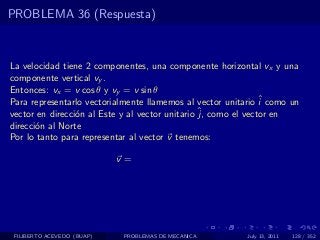
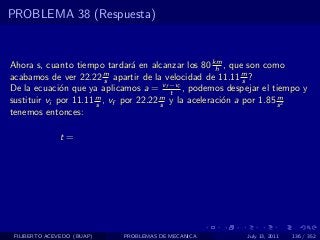
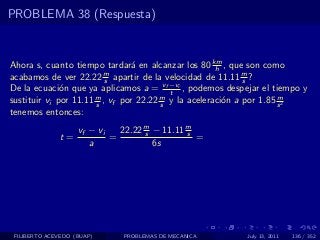
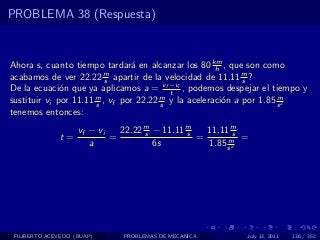
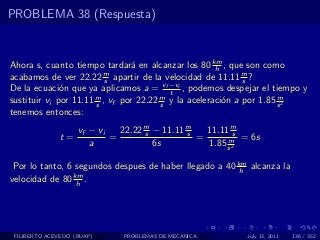
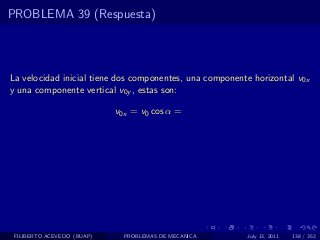
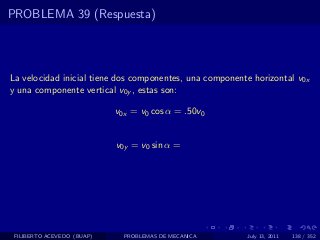
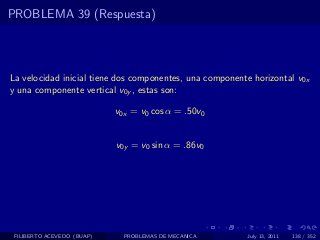
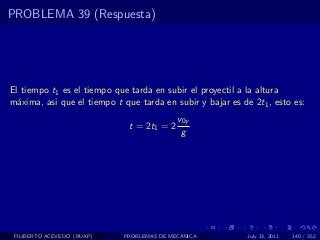
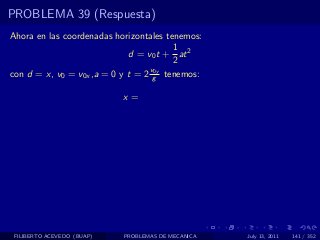
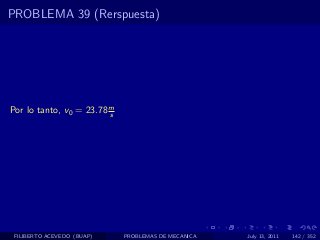
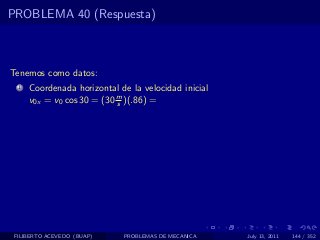
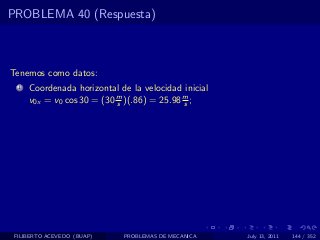
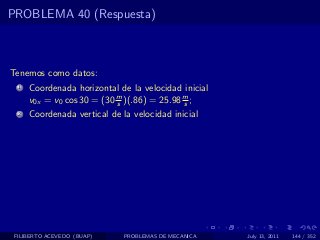
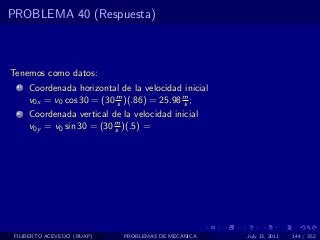
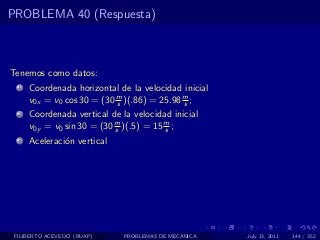
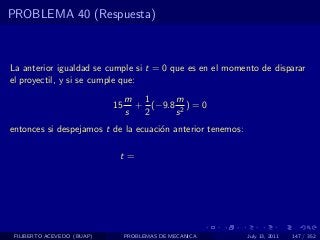
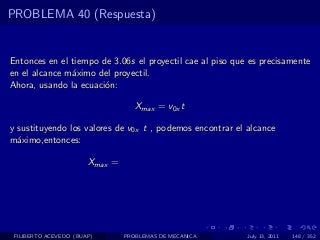
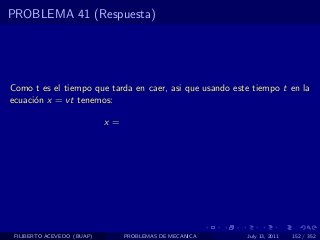
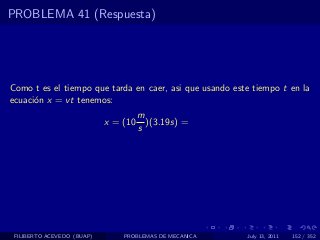
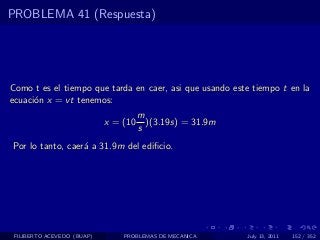
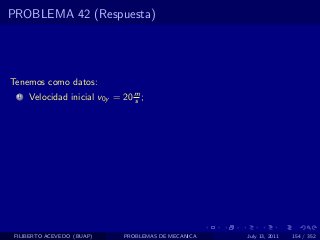
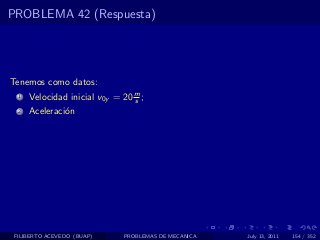
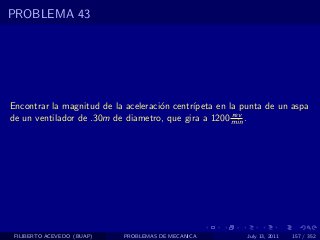
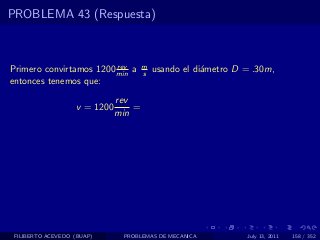
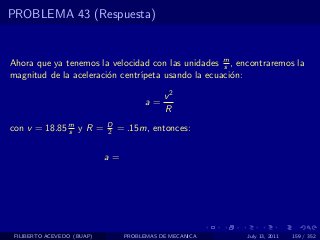
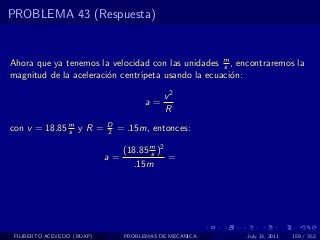
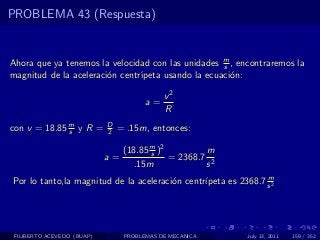
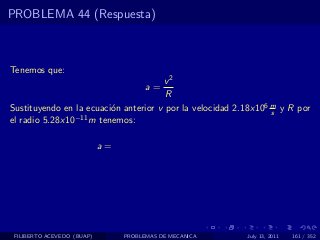
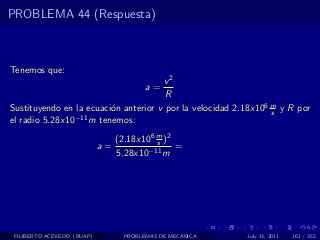
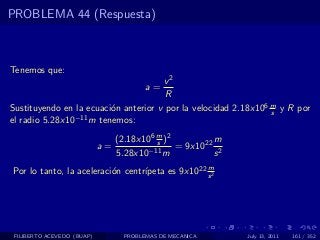
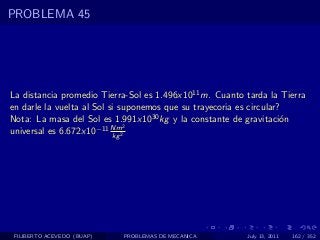
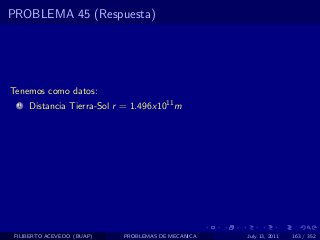
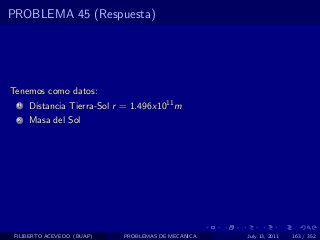
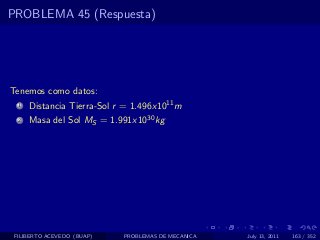
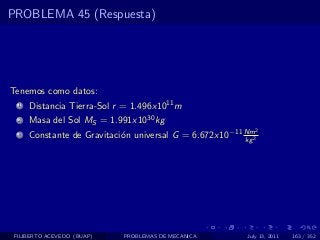
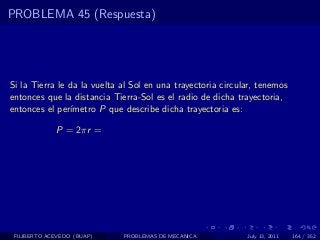
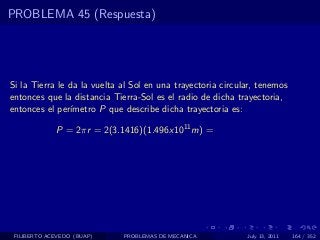
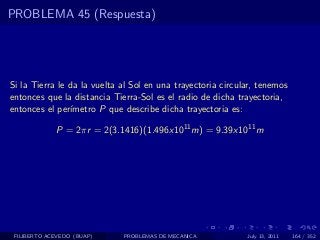
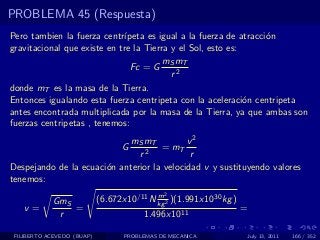
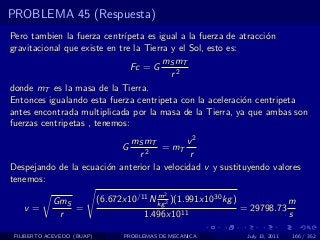
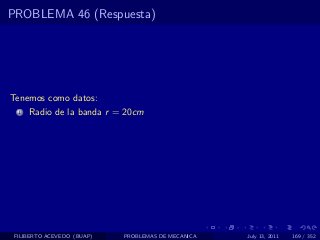
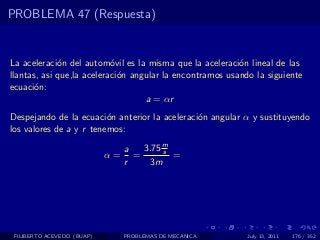
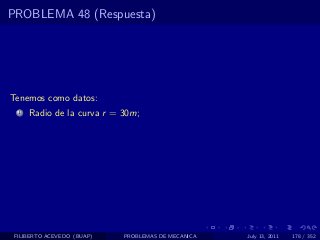
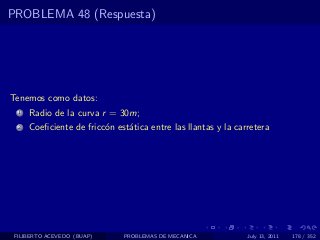
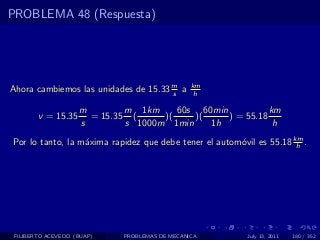
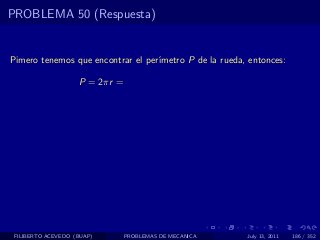
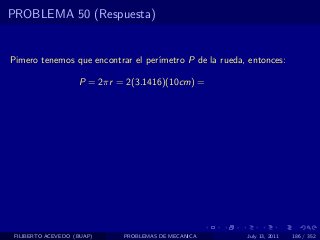
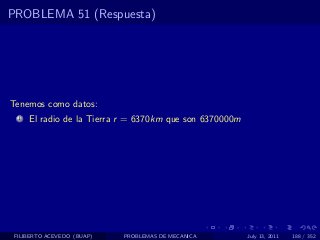
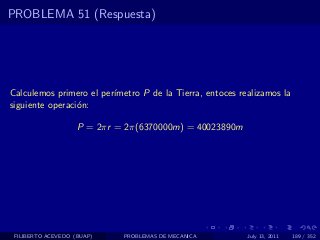
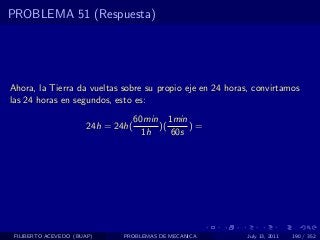
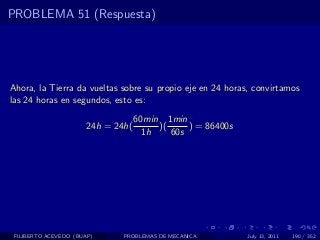
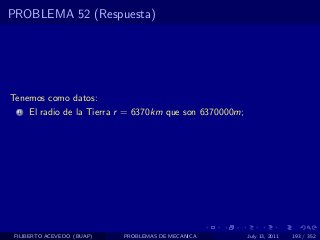
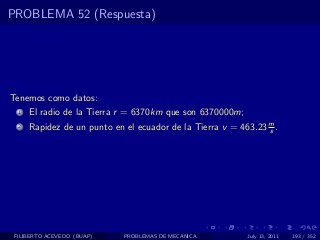
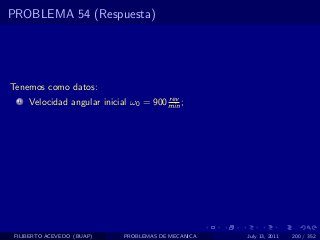
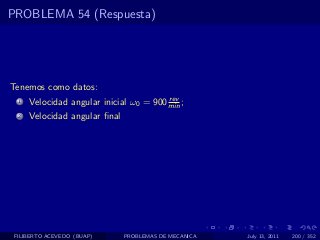
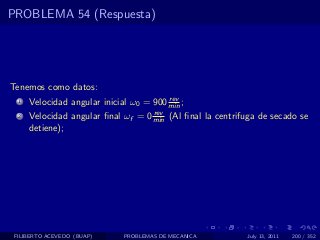
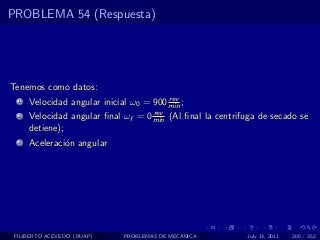
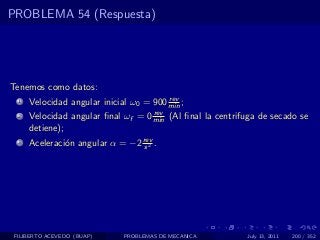
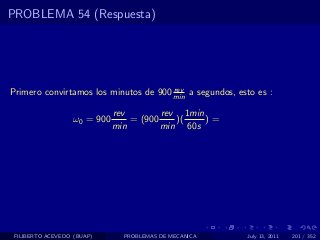
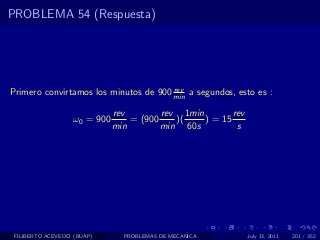
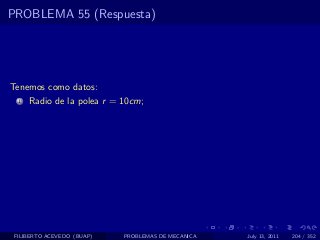
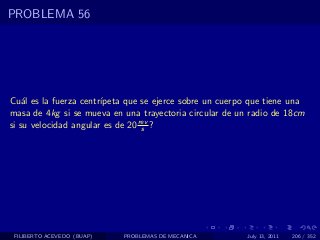
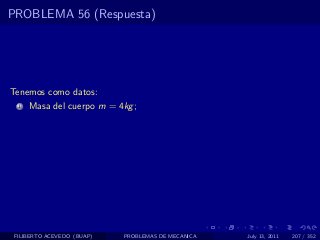
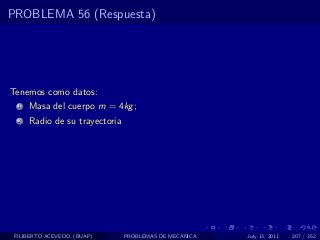
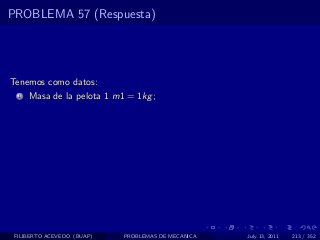
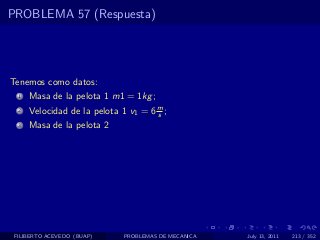
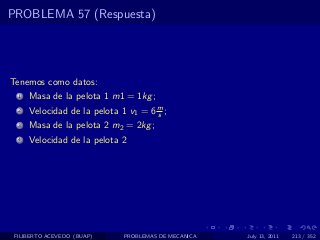
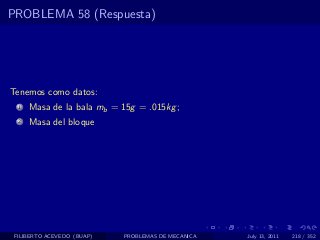
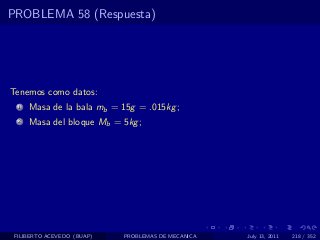
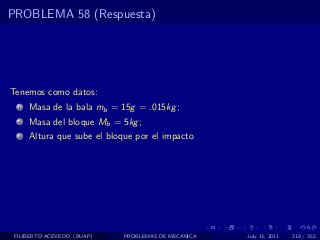
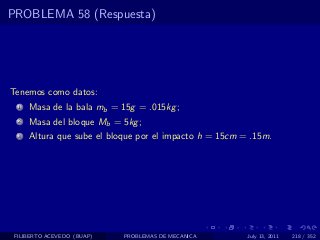
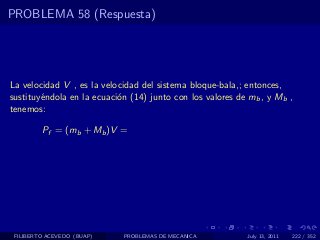
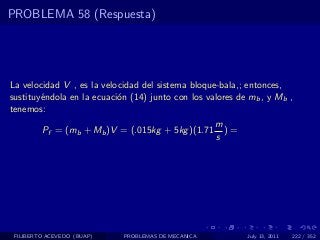
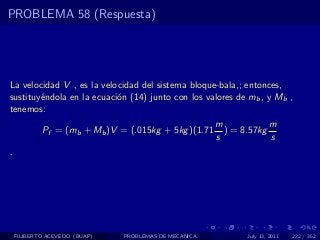
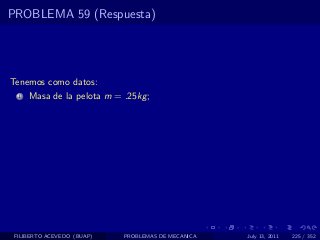
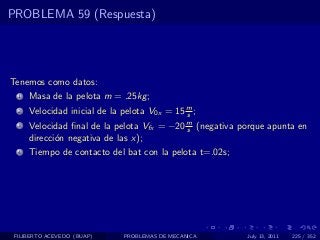
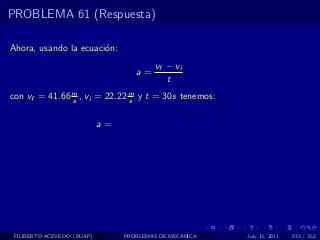
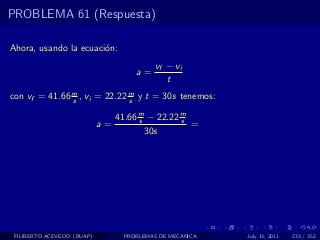
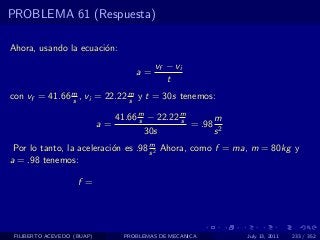
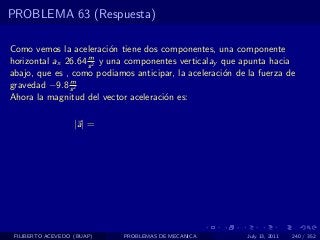
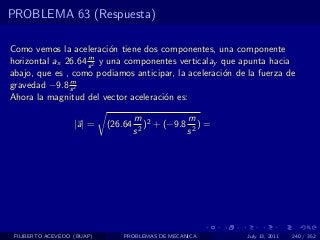
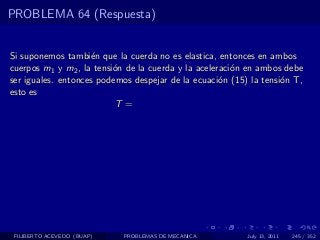
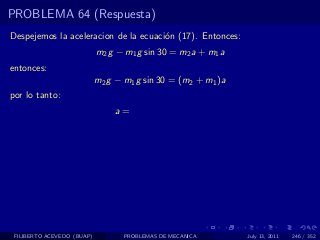
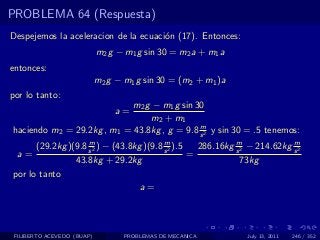
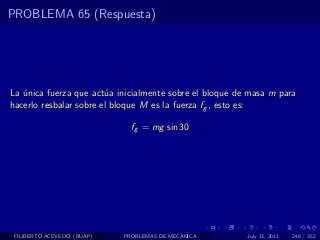
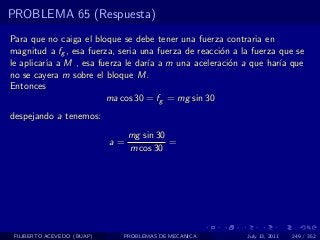
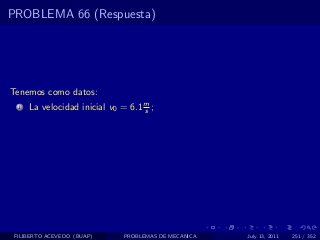
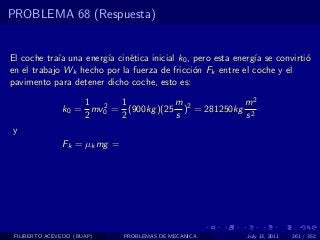
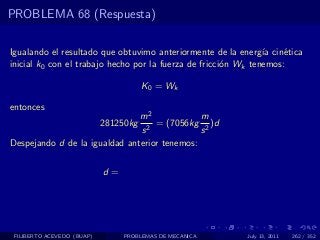
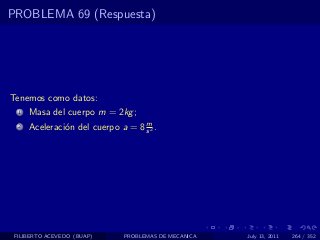
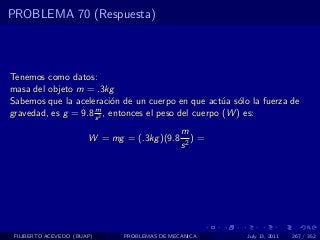
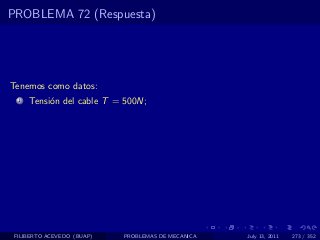
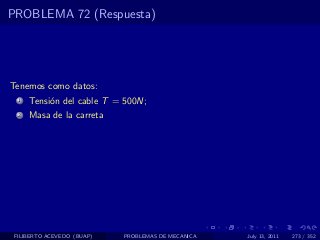
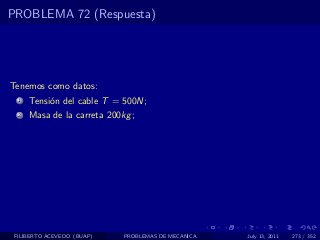
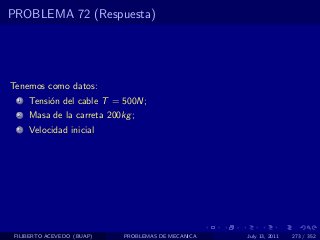
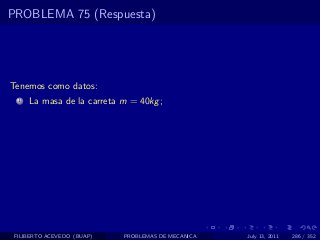
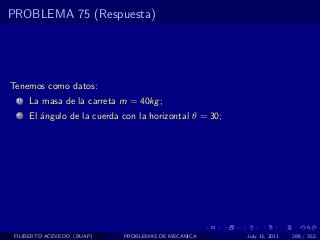
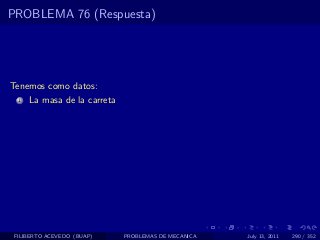
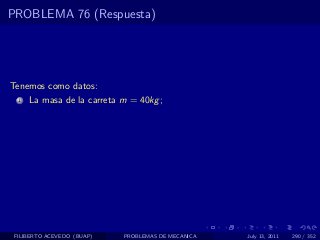
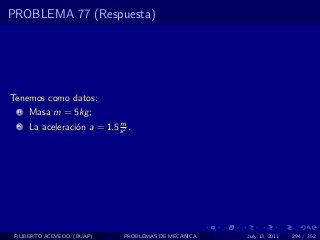
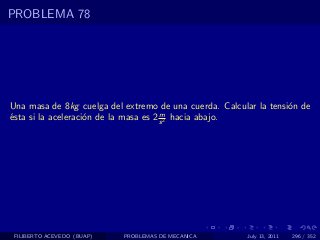
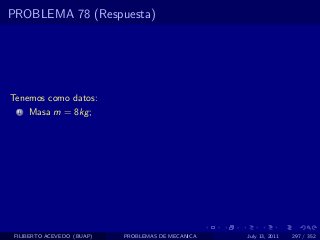
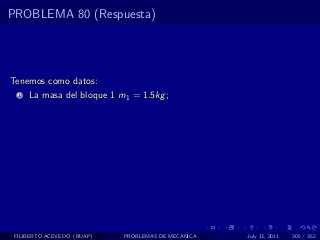
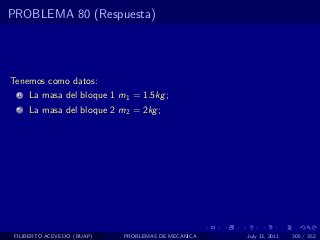
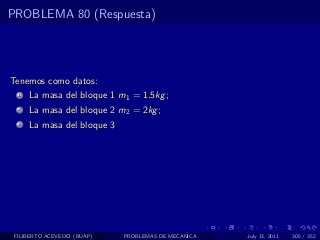
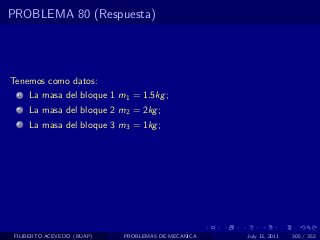
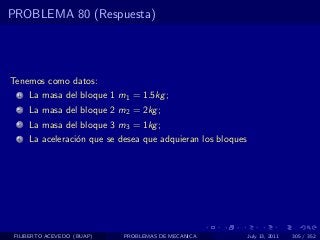
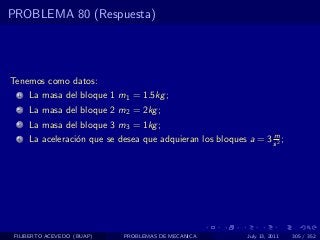
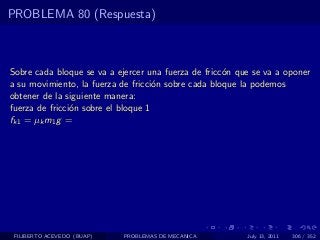
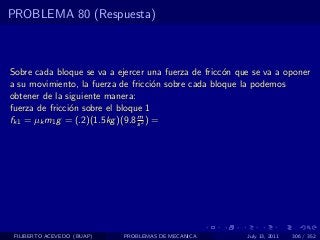
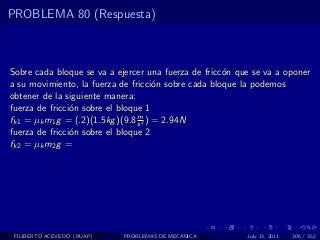
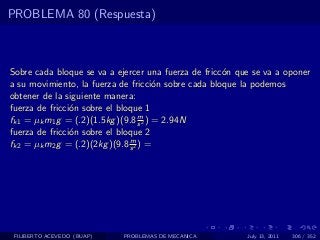
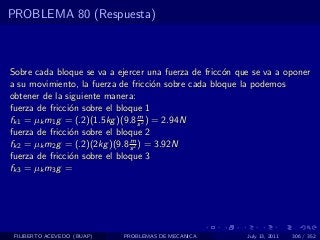
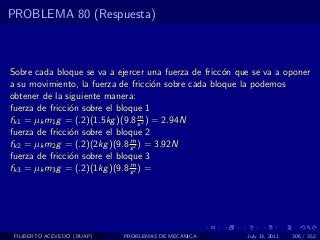
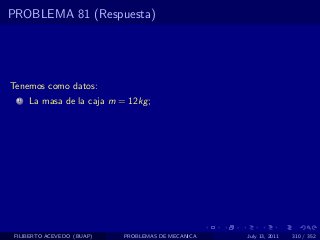
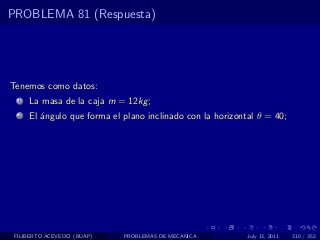
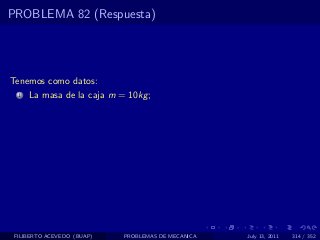
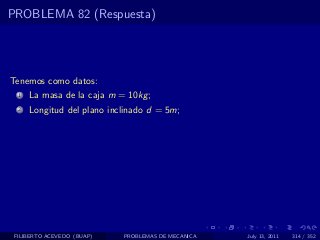
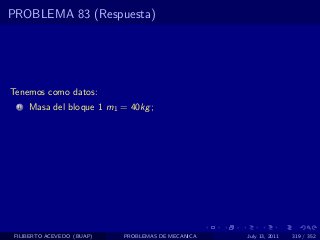
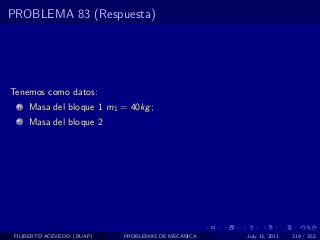
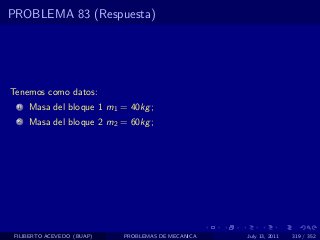
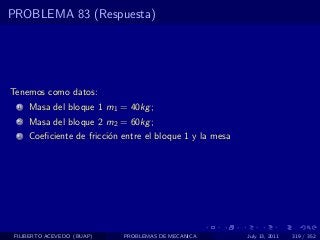
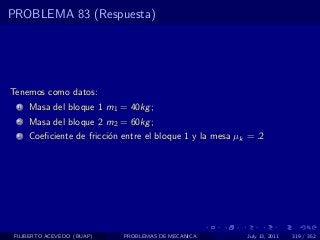
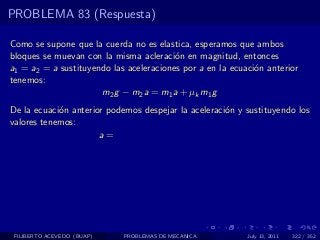
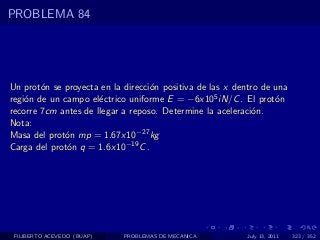
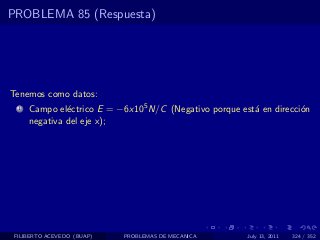
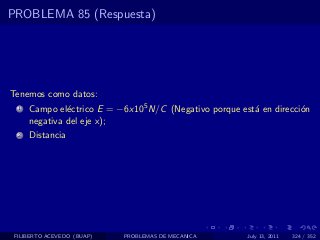
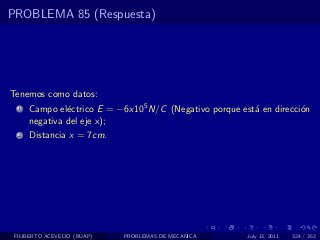
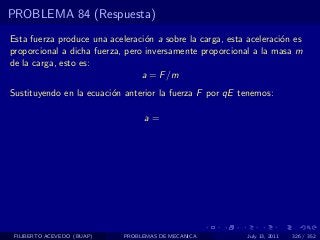
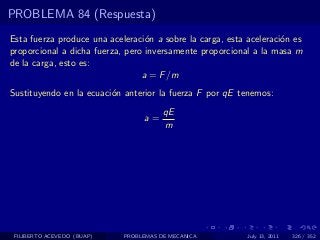
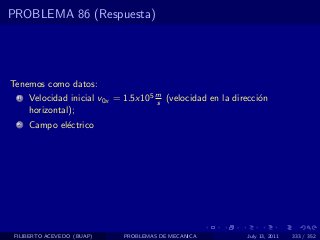
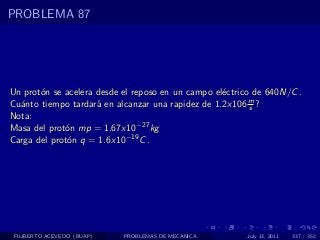
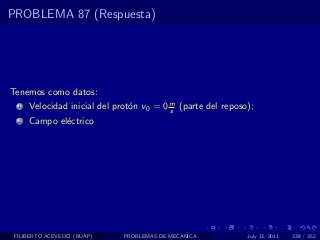
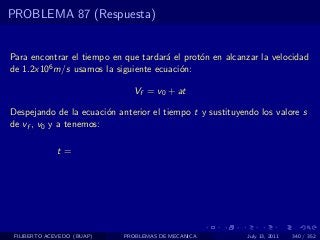
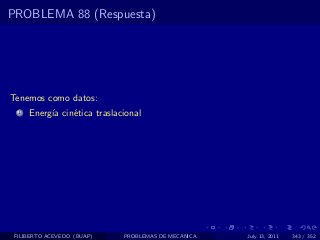
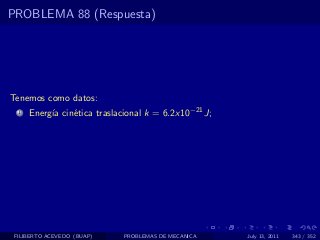
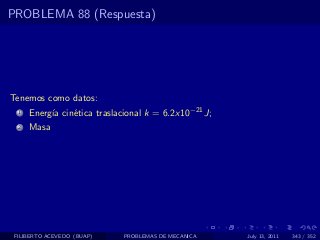
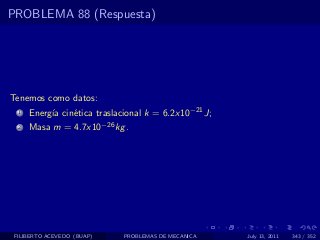
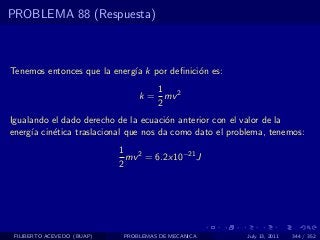
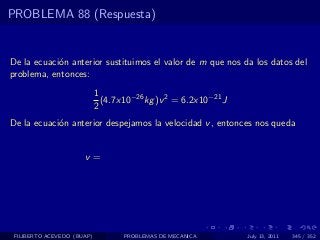
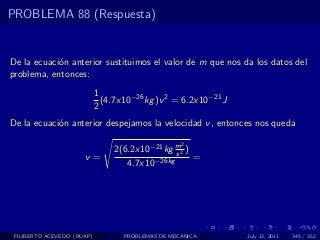
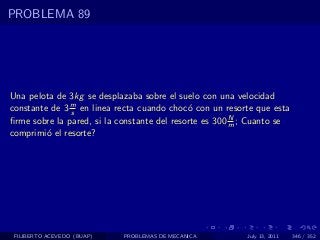
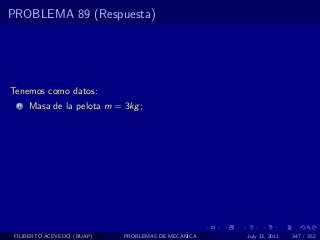
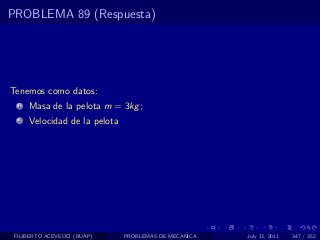
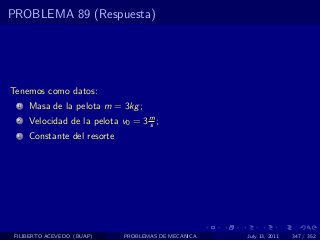
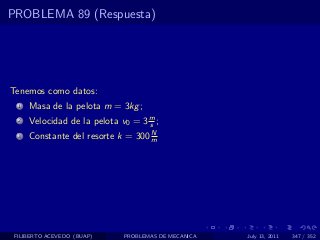
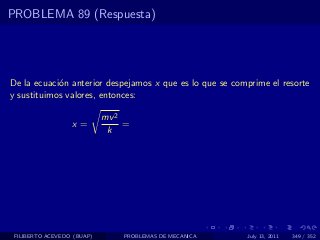
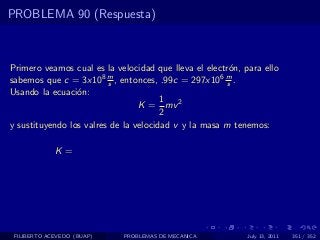
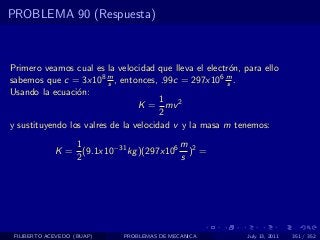
El documento presenta 4 problemas de conversiones de unidades y velocidad que involucran kilómetros, metros, minutos, segundos, grados y revoluciones. Resuelve un quinto problema sobre la velocidad media de un objeto que recorrió dos tramos a velocidades diferentes.