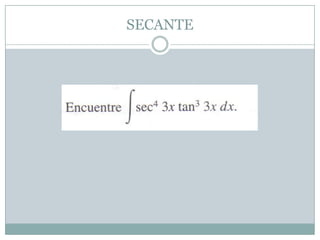
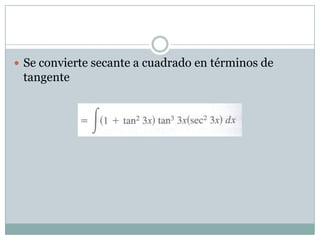
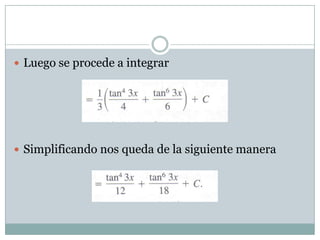
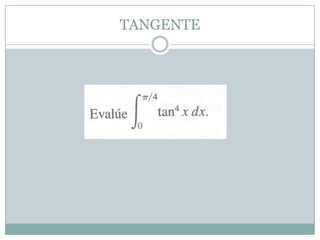
El documento describe dos métodos para resolver integrales con secante y tangente: 1) para secante, se reescribe la integral siguiendo las reglas de secante y se convierte secante al cuadrado en términos de tangente, resultando en una integral que se puede resolver; 2) para tangente, se reescribe la integral, se pasa un tangente en términos de secante y se separa en dos integrales, convirtiendo el segundo tangente cuadrado a términos de secante y resolviendo ambas integrales con métodos básicos.

1. RESOLUCIÓN DE INTEGRALES CON SECANTE
Y TANGENTE

2. SECANTE

3.  Se reescribe la integral siguiendo los lineamientos de
la secante

4.  Se convierte secante a cuadrado en términos de
tangente

5.  Se recuerda trabajar la regla de la cadena y da como
resultado este

6.  Luego se procede a integrar
 Simplificando nos queda de la siguiente manera

7. TANGENTE

8.  Primeramente se reescribe la integral de la siguiente
forma
 Se procede a pasar un tangente en terminos de
secante

9.  Separamos en dos integrales
 Convertimos el segundo tangente cuadrado a
términos de secante

10.  La primer integral se resuelve con forme el
lineamiento y la segunda se separa en otras dos y se
trabaja conforme a las integrales básicas