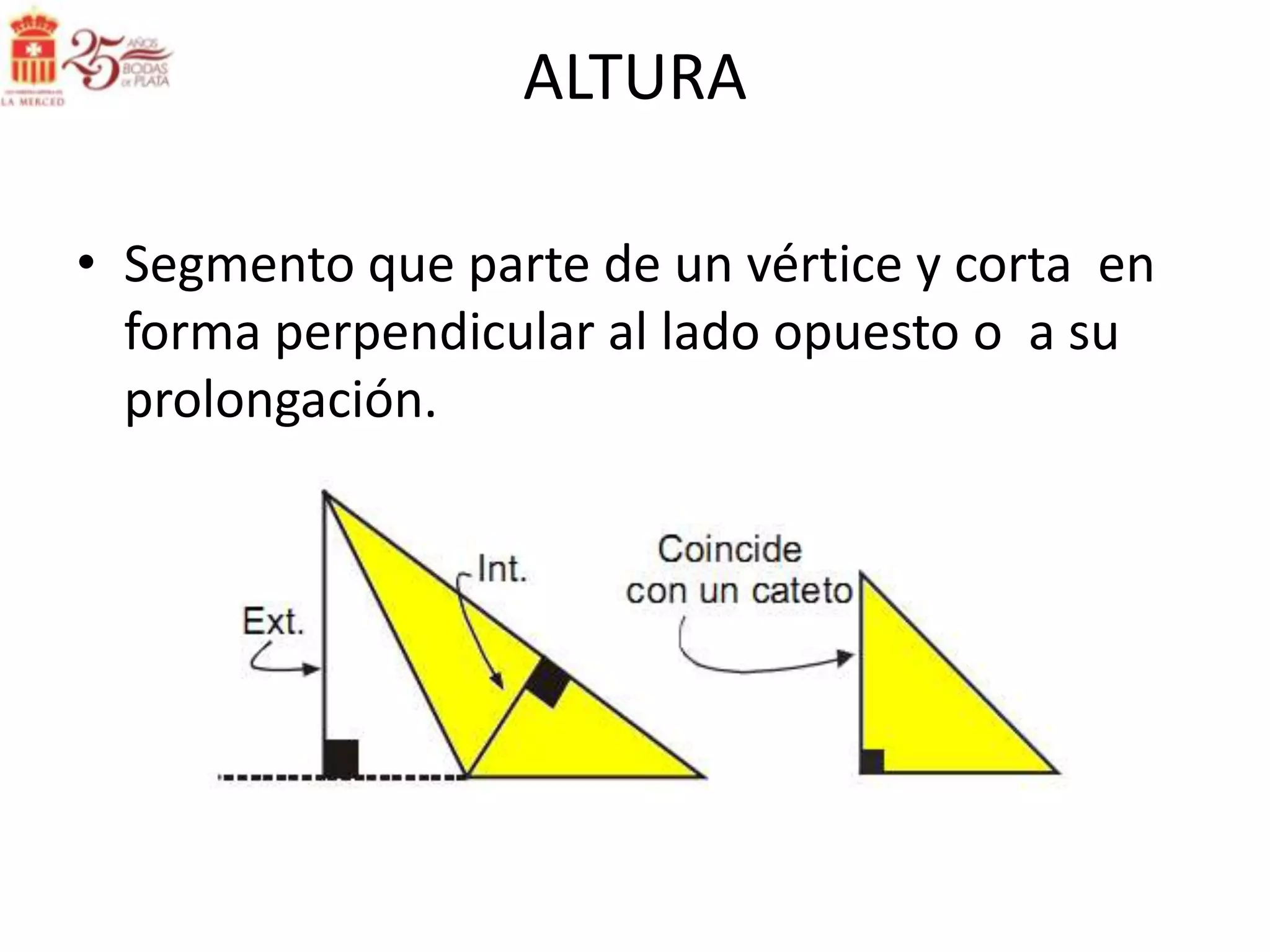
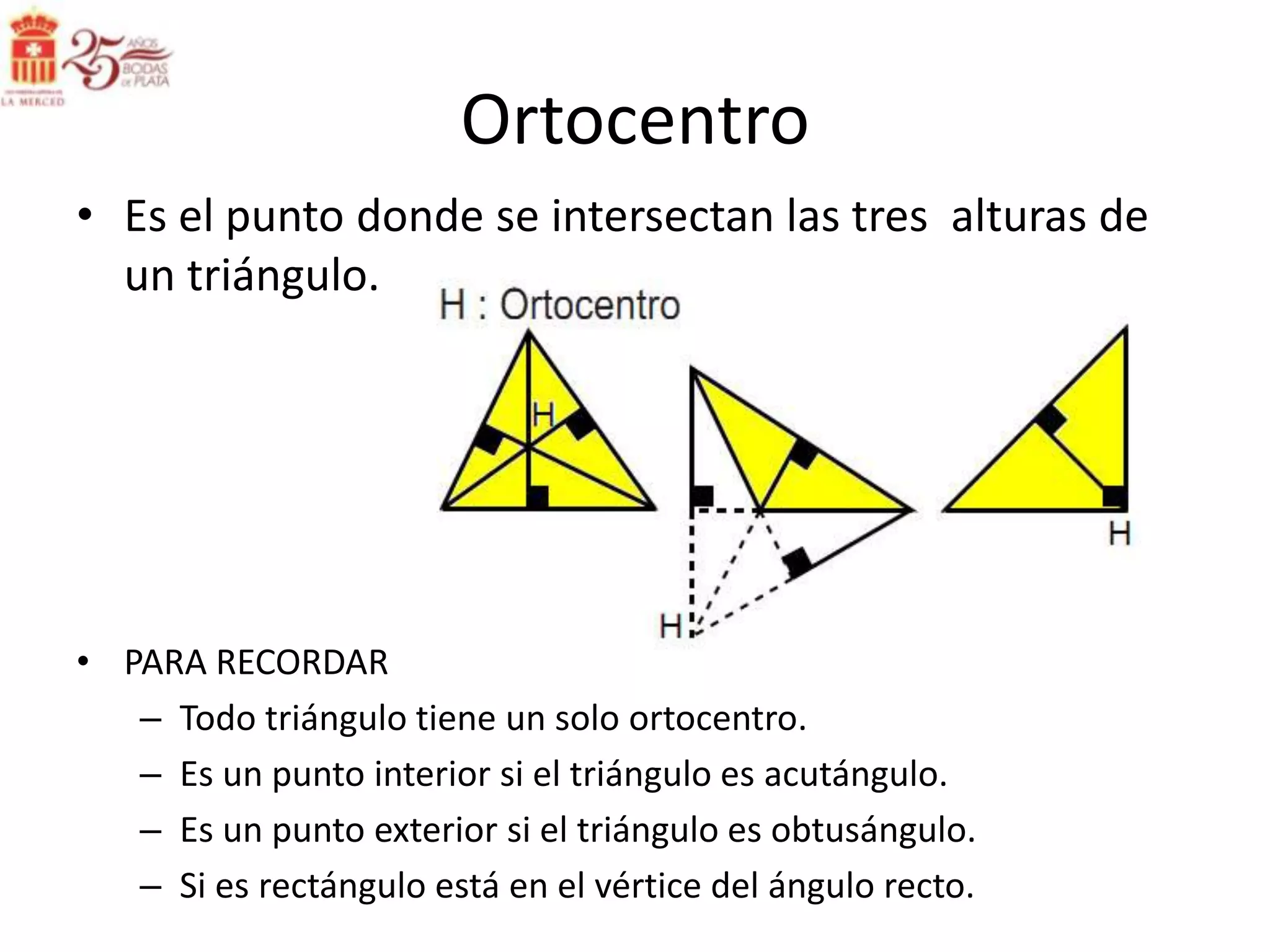
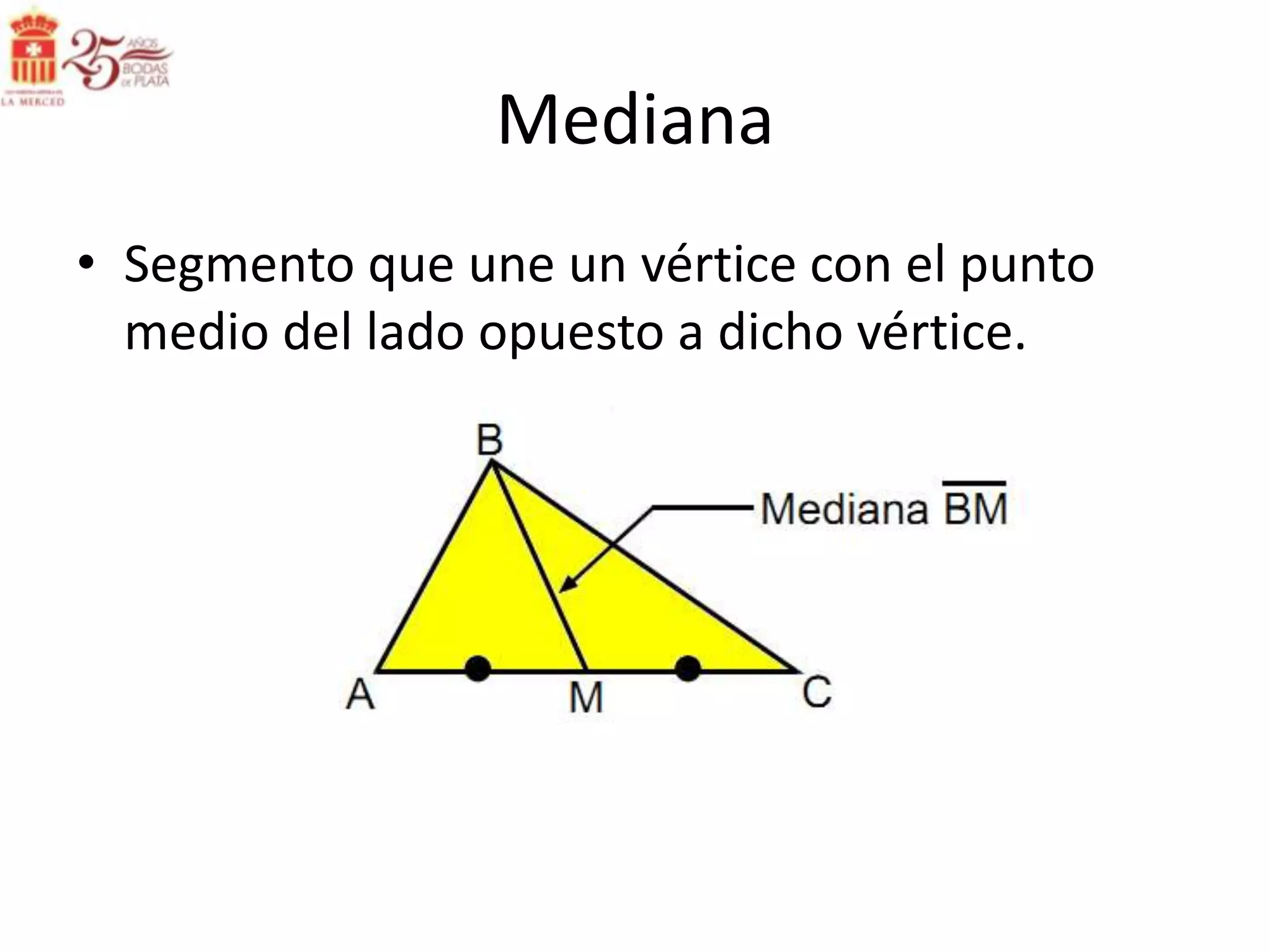
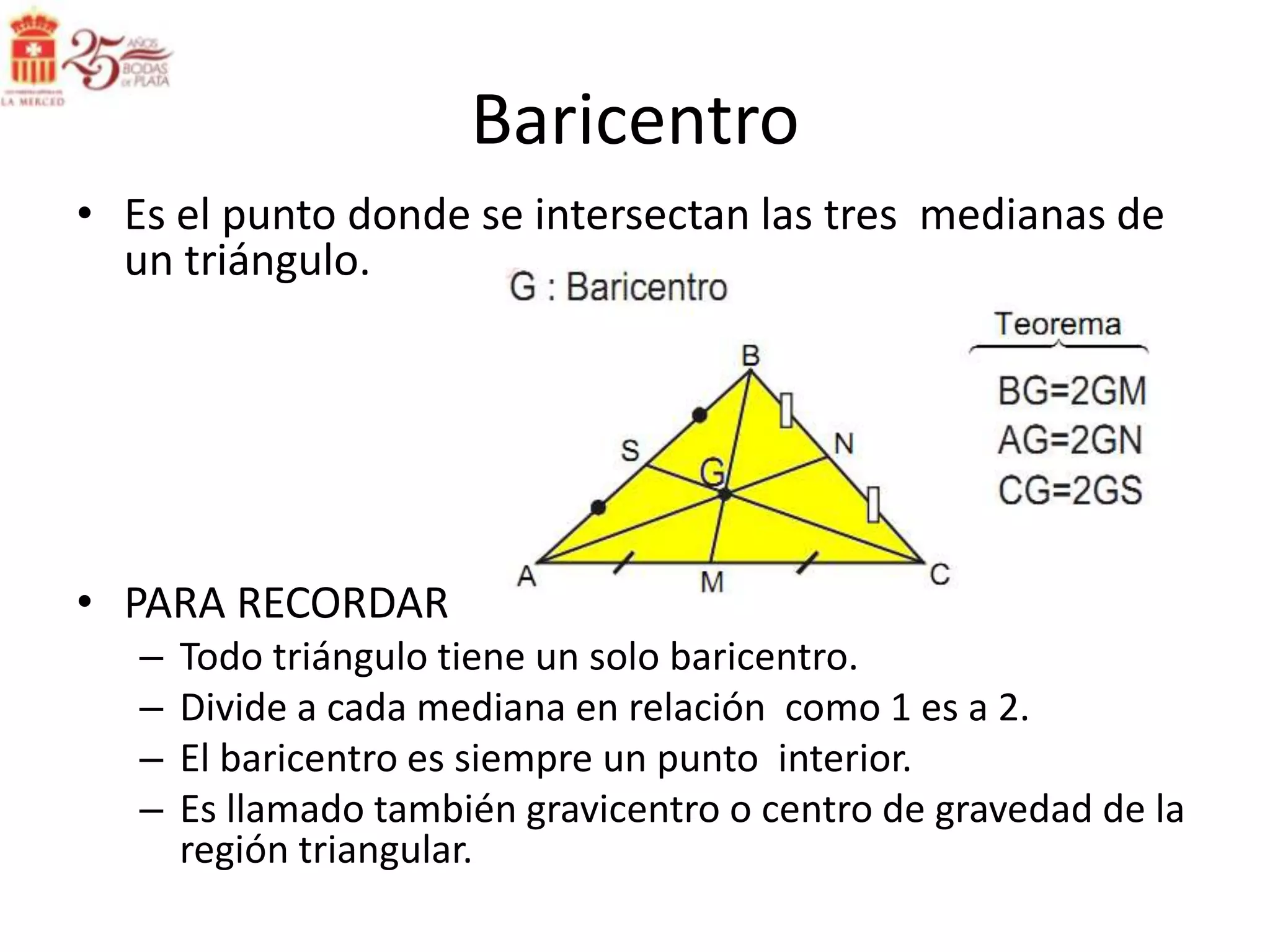
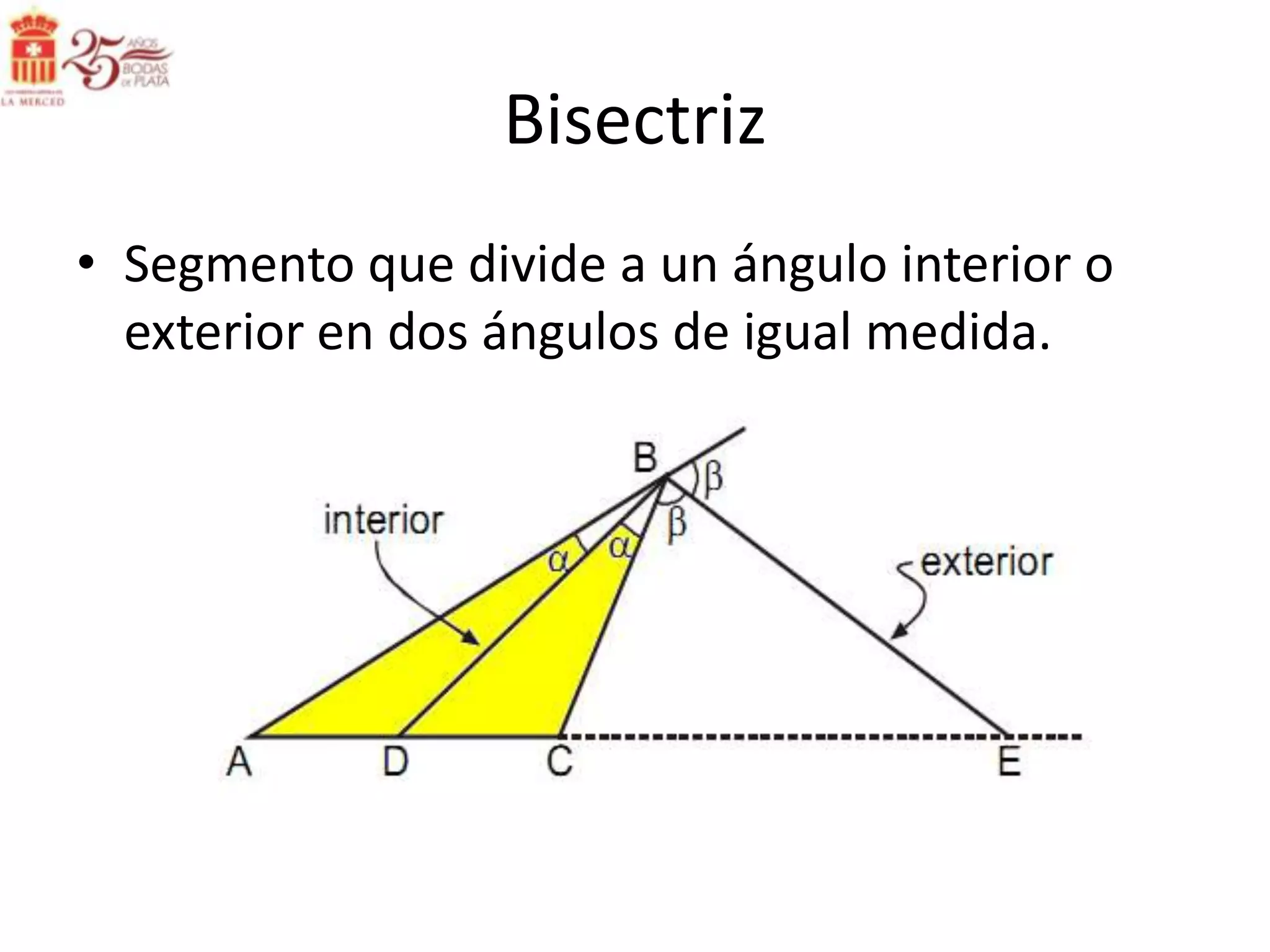
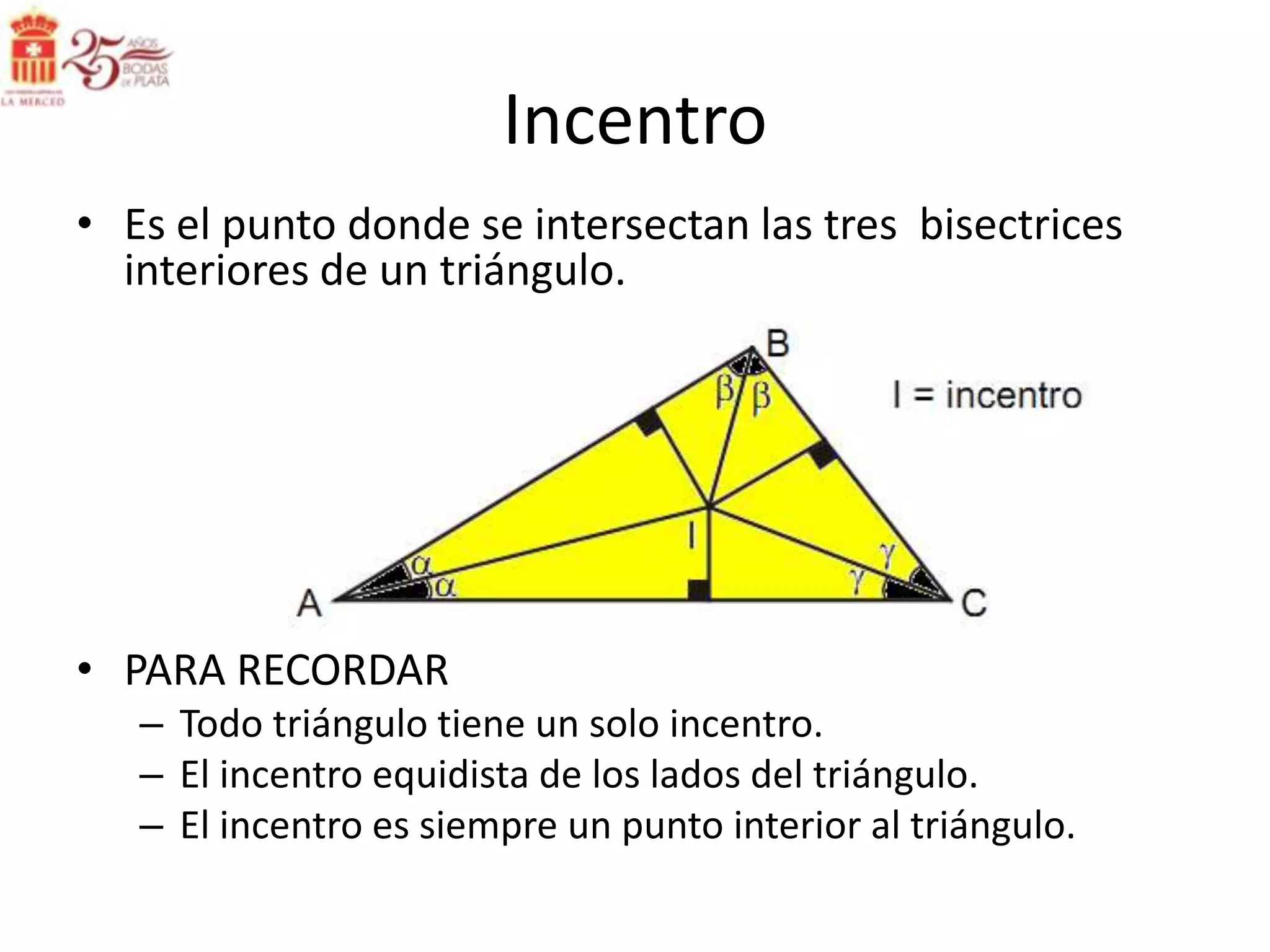
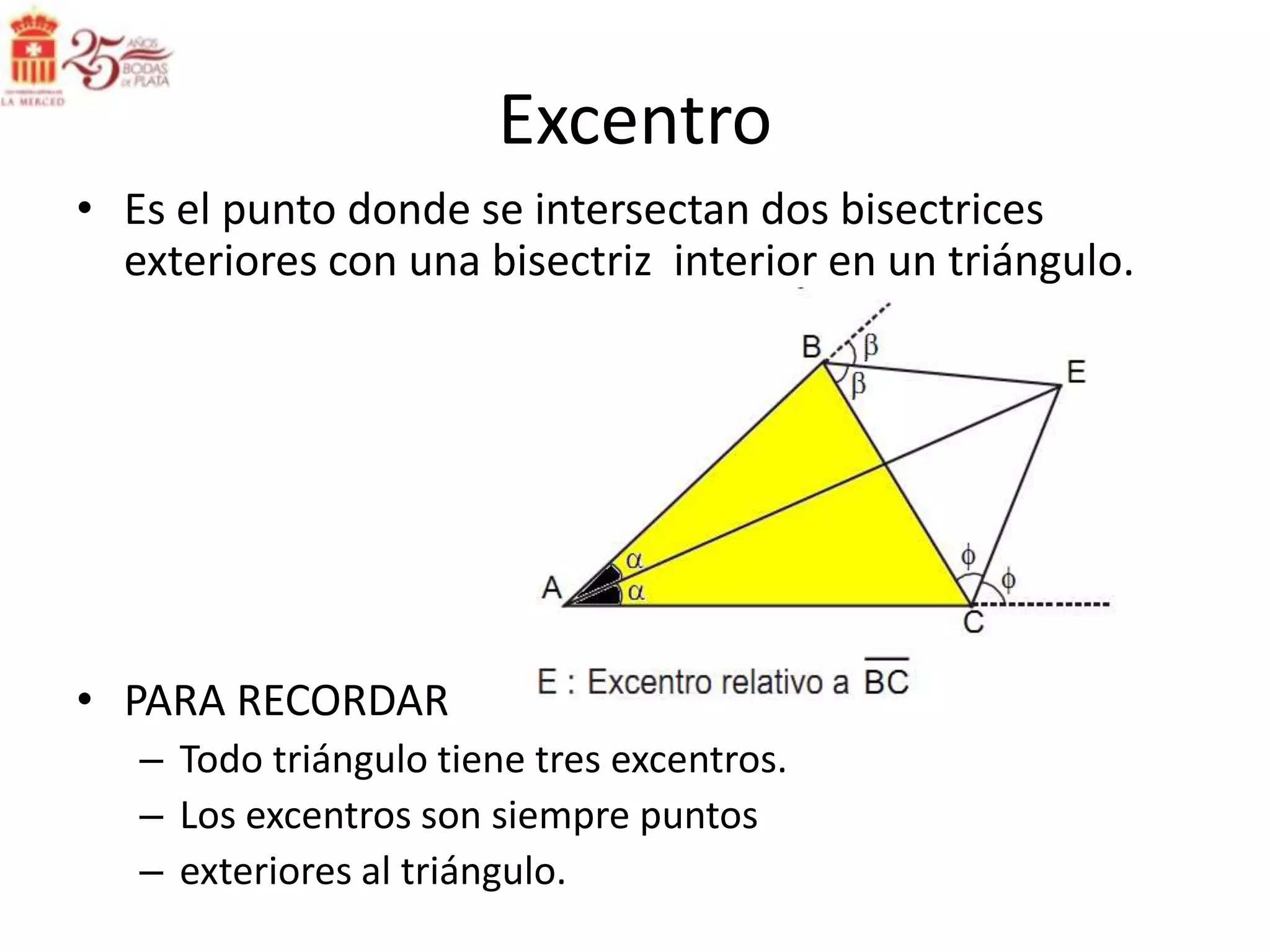
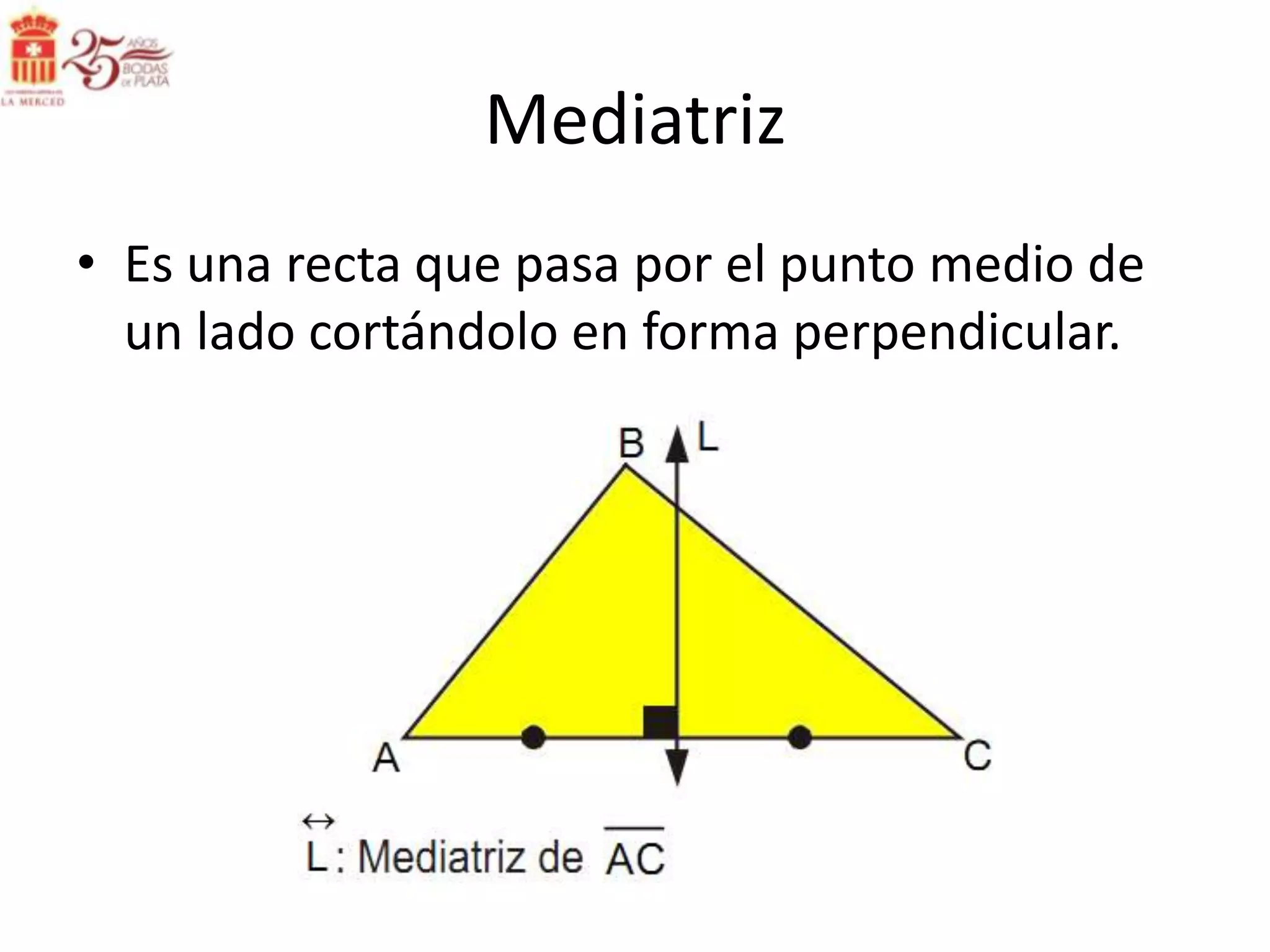
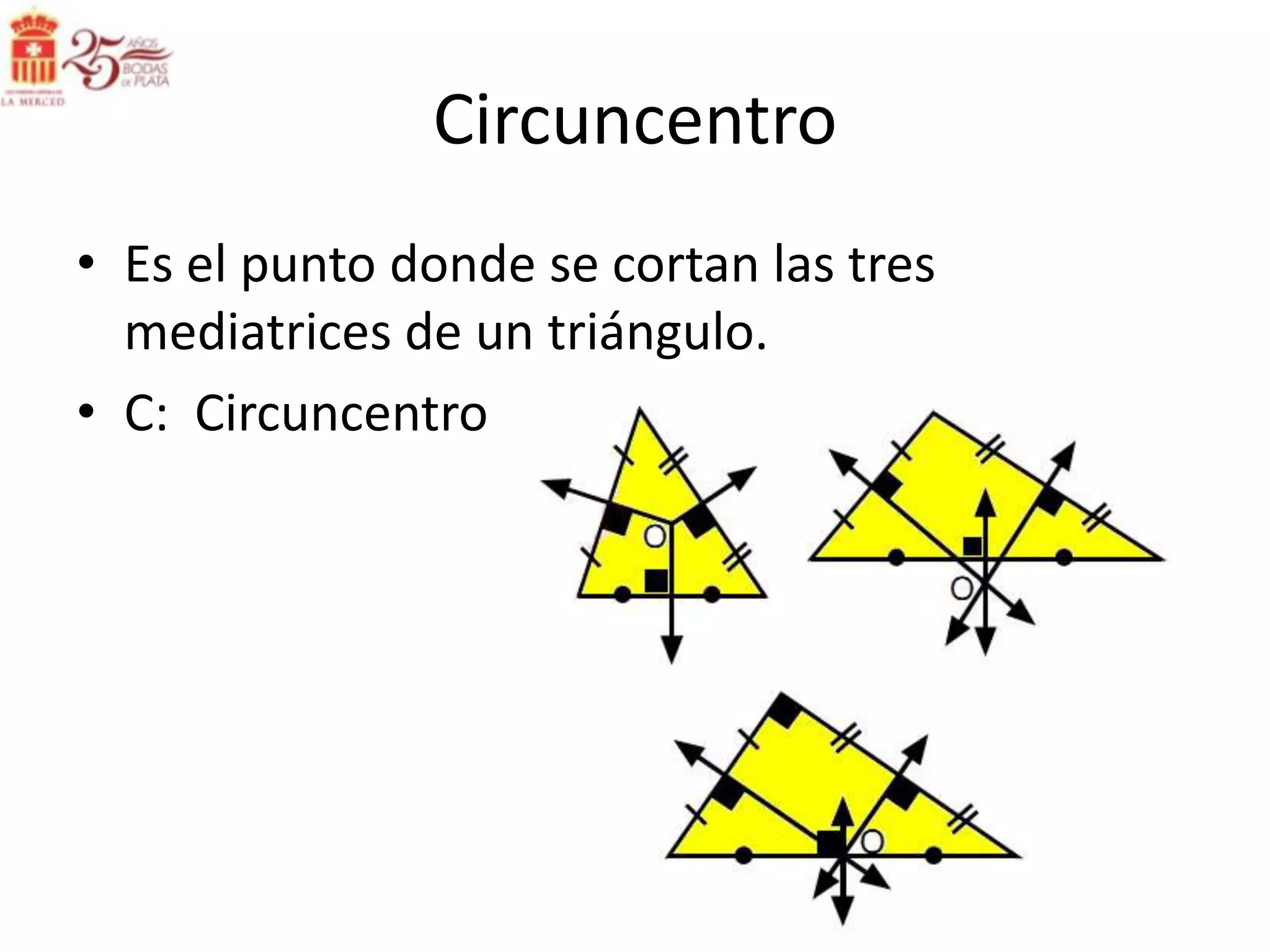
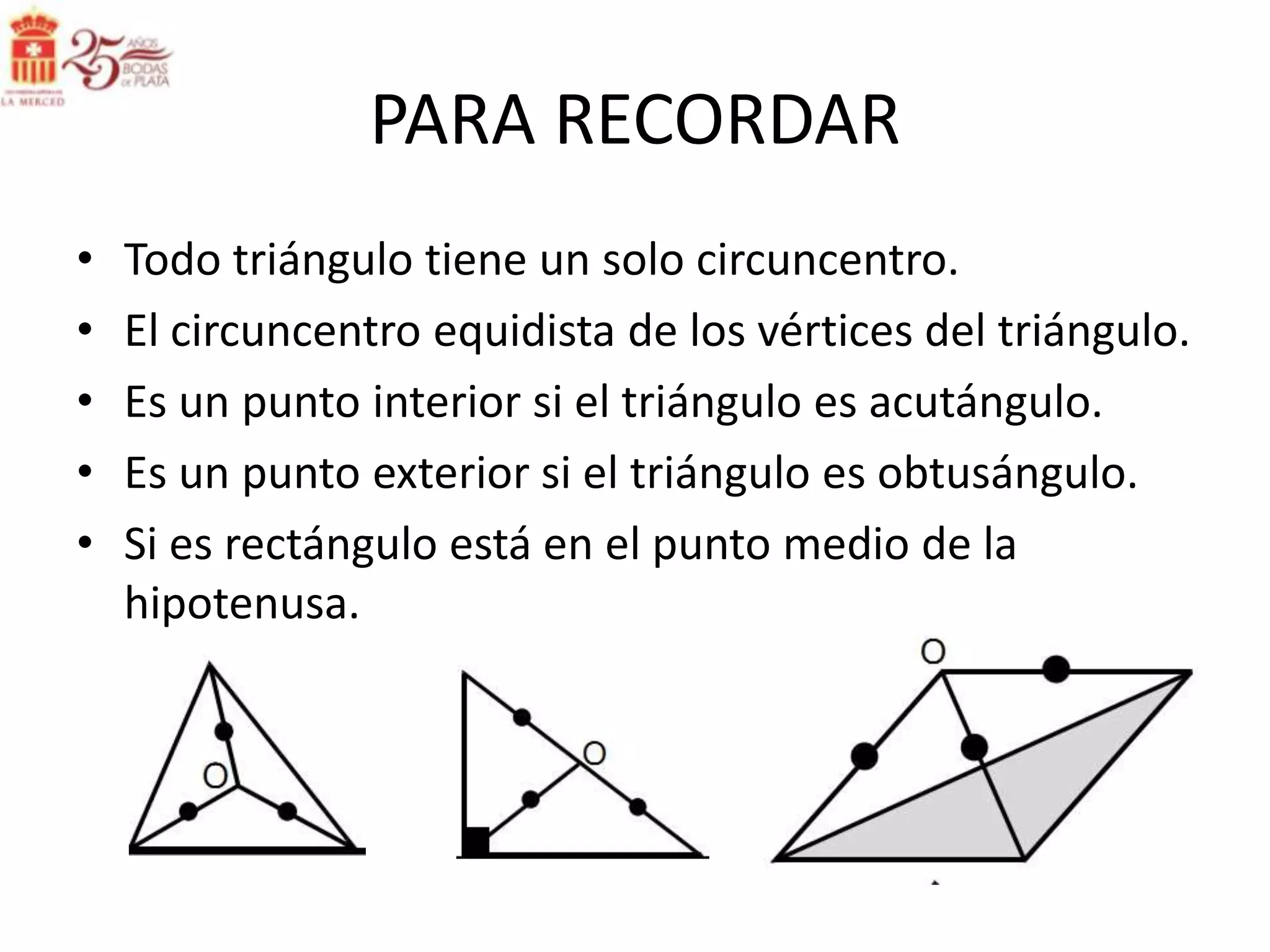
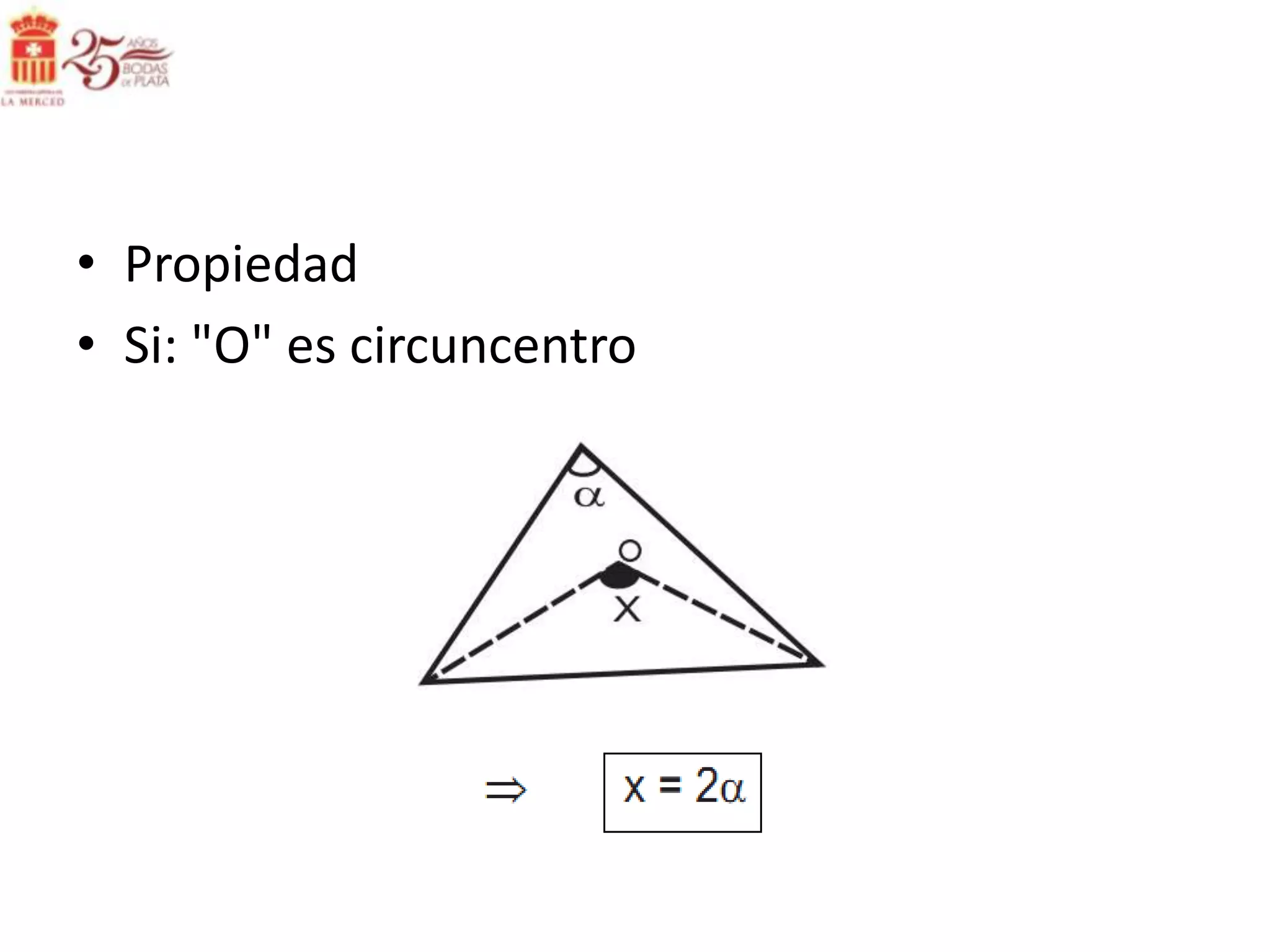
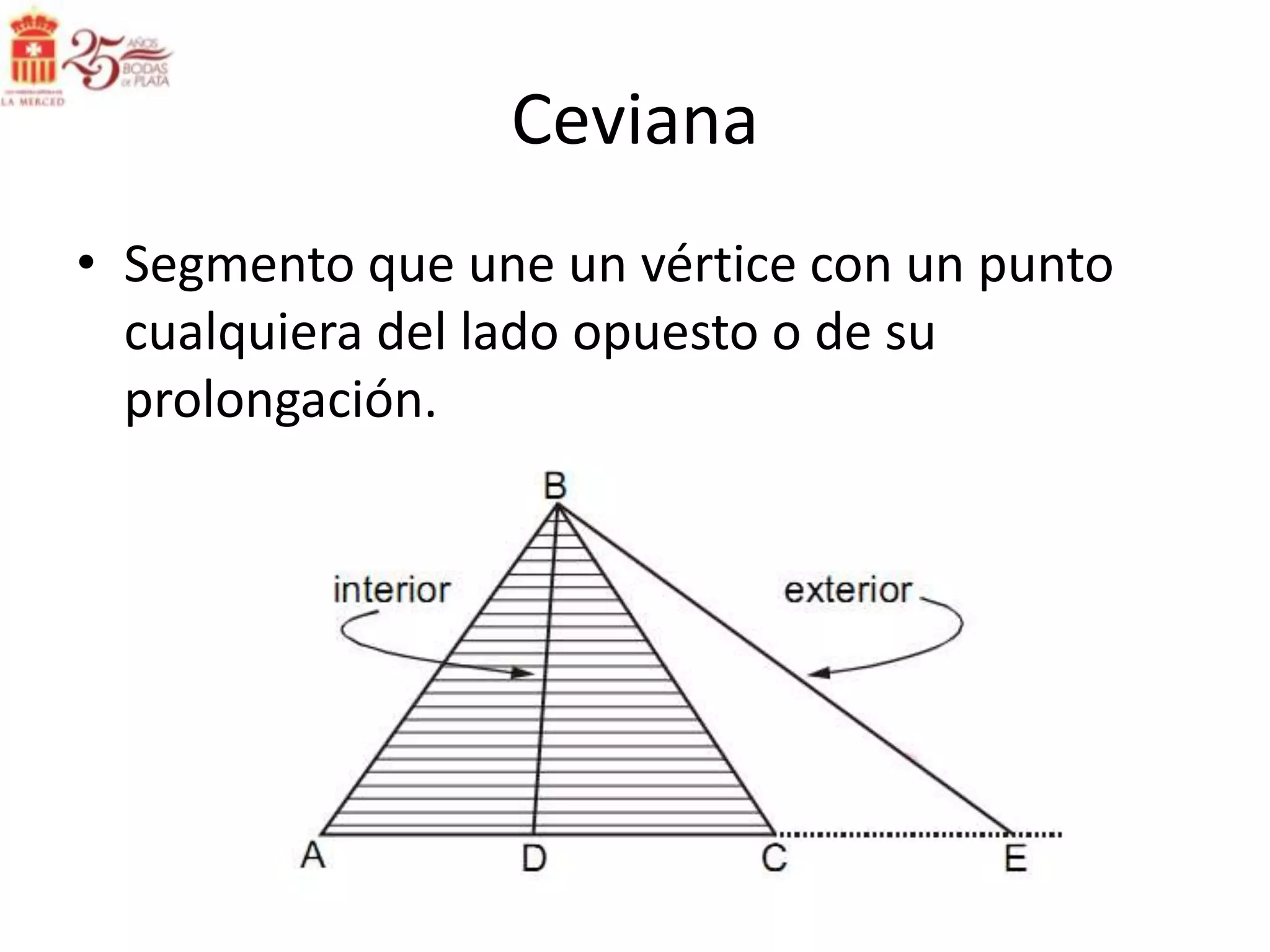
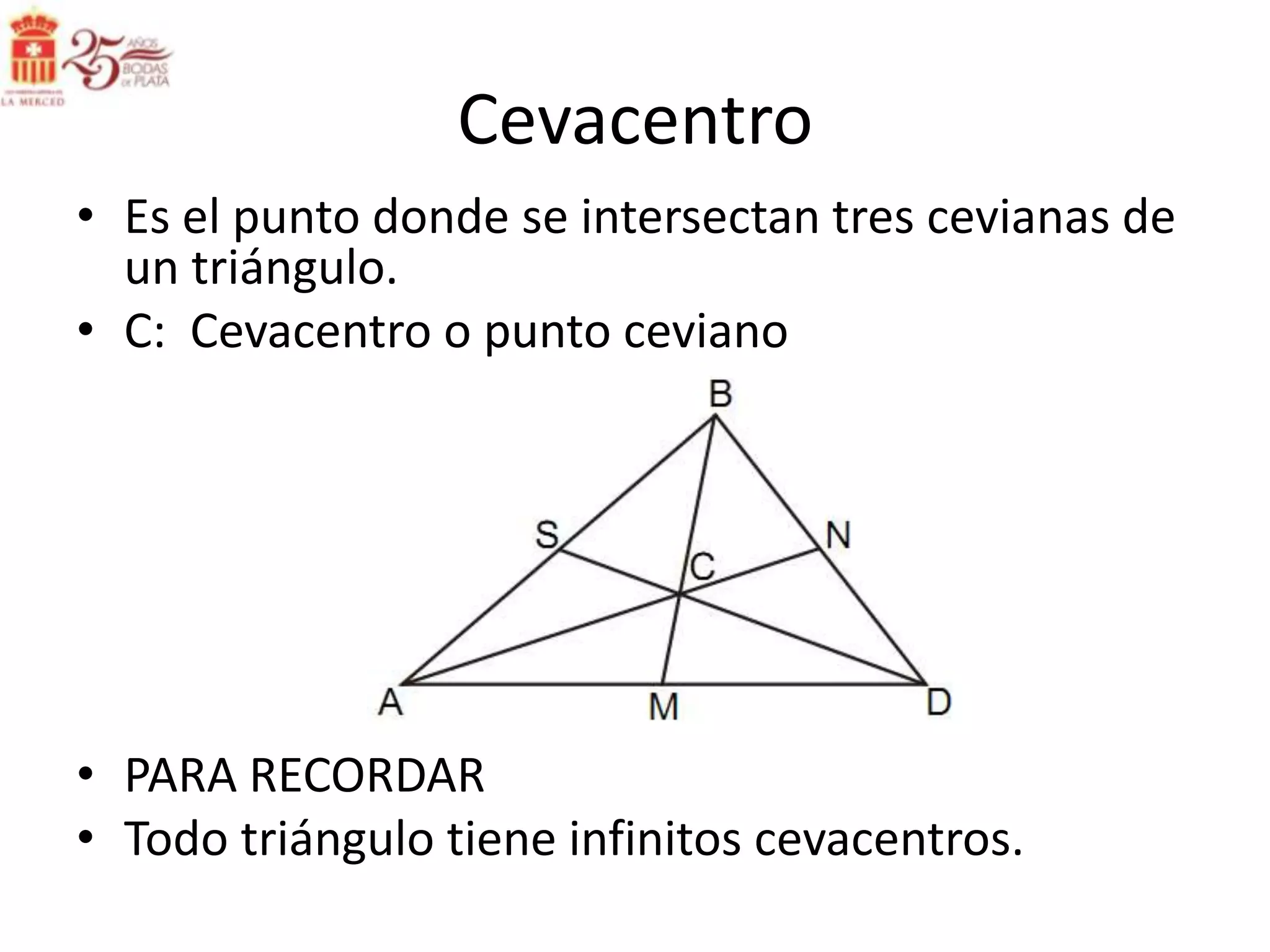
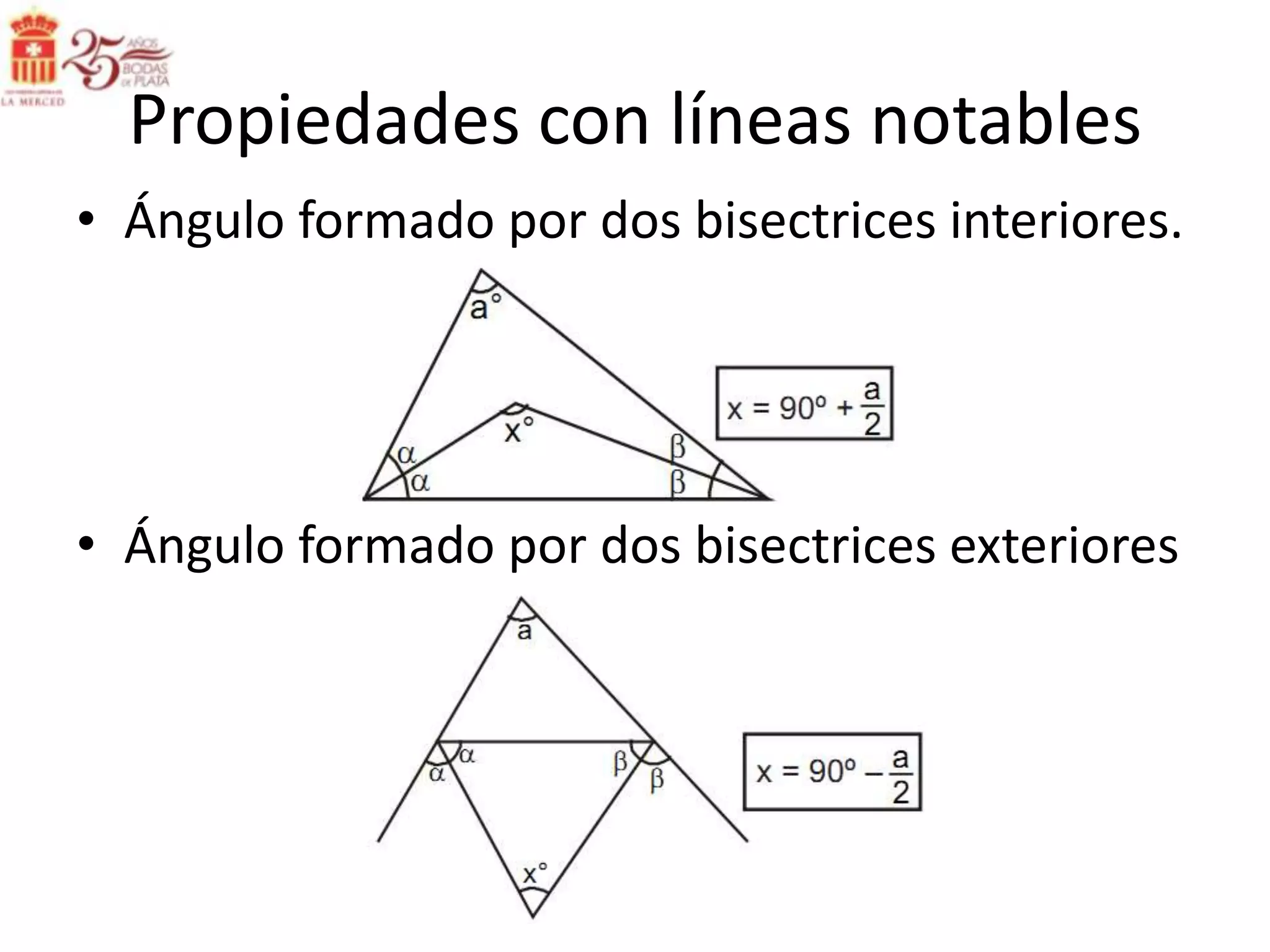
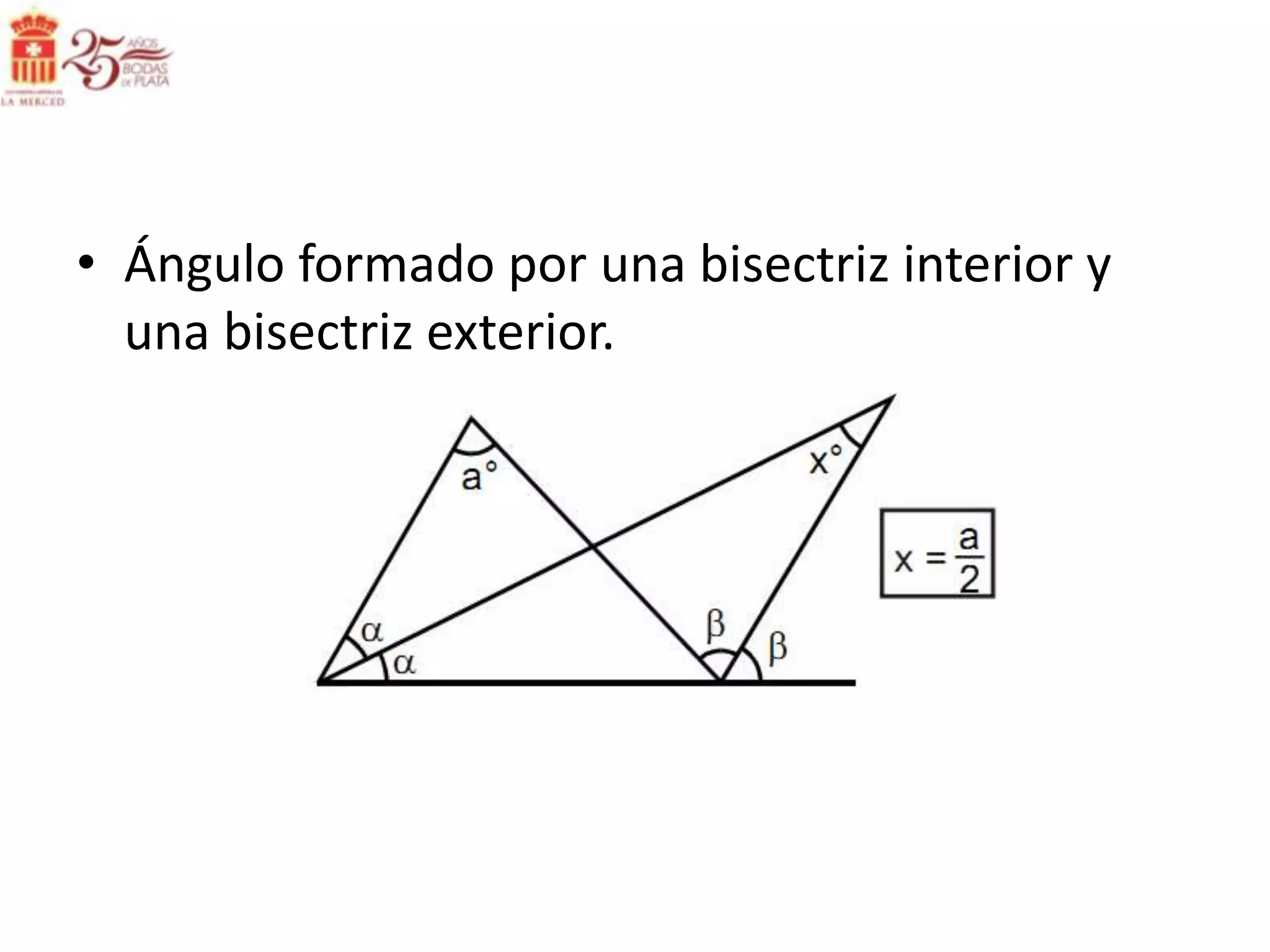
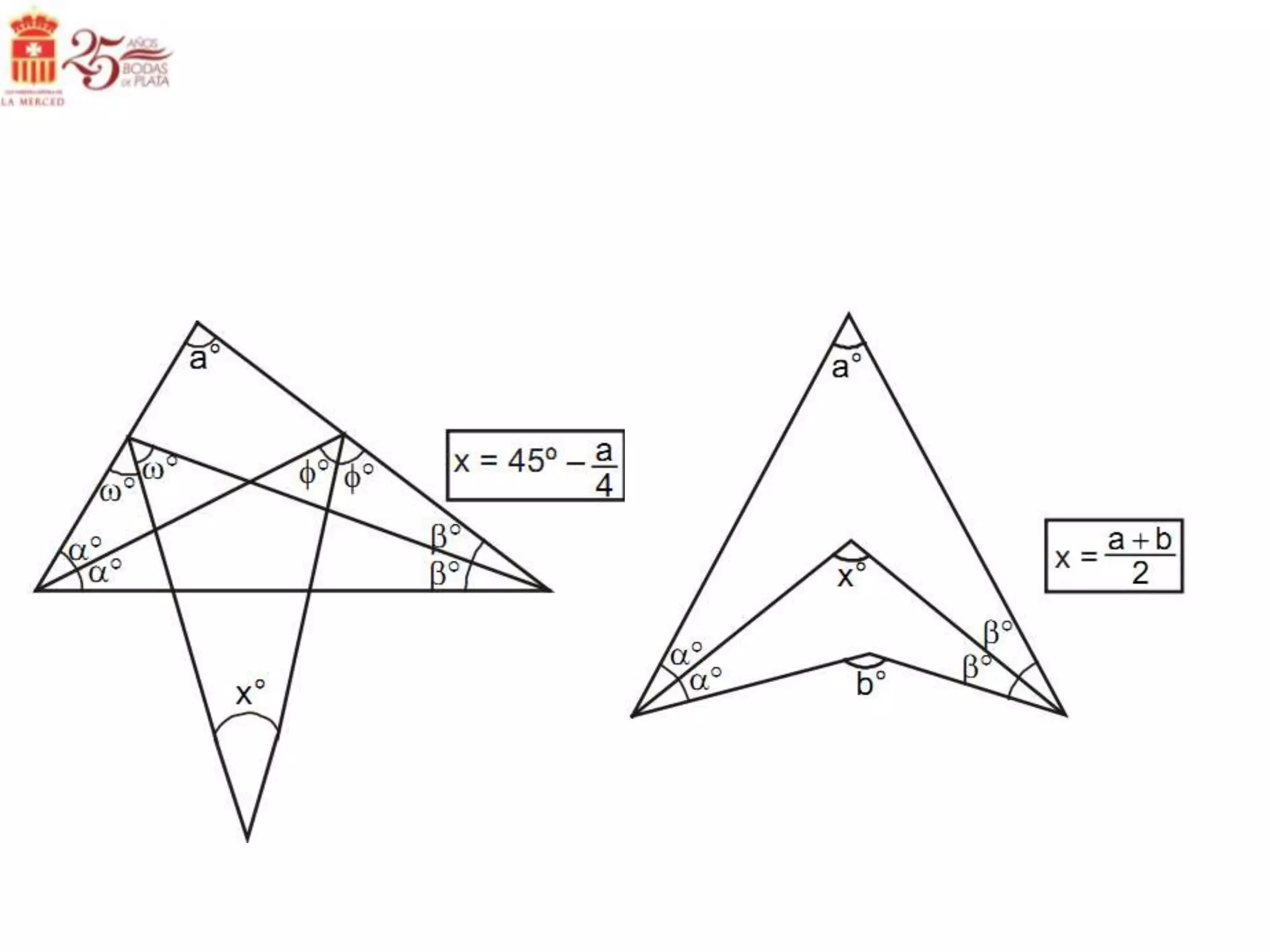
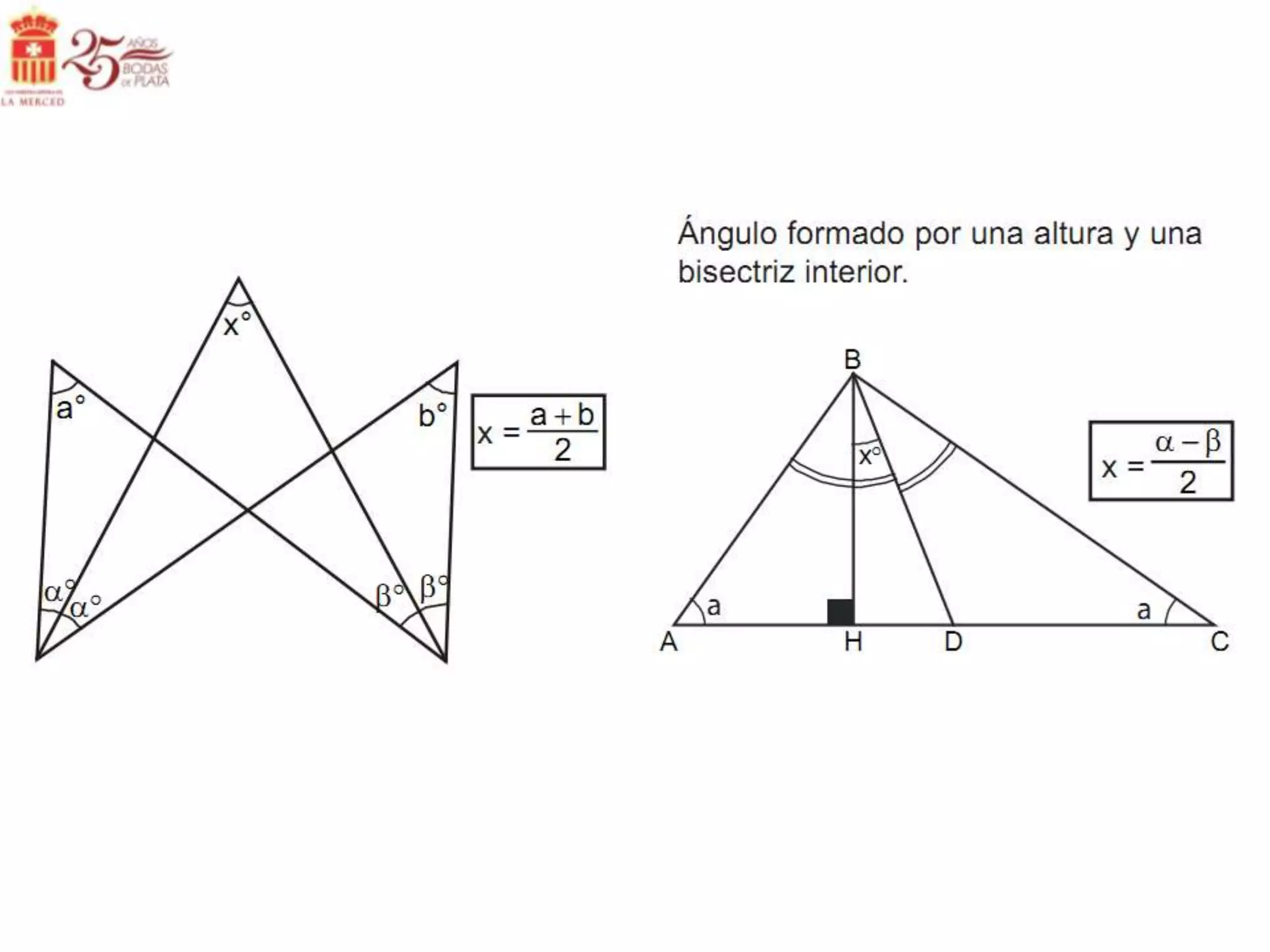
Este documento describe las líneas notables en los triángulos, incluyendo la altura, ortocentro, mediana, baricentro, bisectriz, incentro, excentro, mediatriz y circuncentro. Explica dónde se intersectan estas líneas y proporciona propiedades clave para recordar sobre cada una.

1. TRIÁNGULOS: Líneas Notables
Villa El Salvador, marzo 2013

2. ALTURA
• Segmento que parte de un vértice y corta en
forma perpendicular al lado opuesto o a su
prolongación.

3. Ortocentro
• Es el punto donde se intersectan las tres alturas de
un triángulo.
• PARA RECORDAR
– Todo triángulo tiene un solo ortocentro.
– Es un punto interior si el triángulo es acutángulo.
– Es un punto exterior si el triángulo es obtusángulo.
– Si es rectángulo está en el vértice del ángulo recto.

4. Mediana
• Segmento que une un vértice con el punto
medio del lado opuesto a dicho vértice.

5. Baricentro
• Es el punto donde se intersectan las tres medianas de
un triángulo.
• PARA RECORDAR
– Todo triángulo tiene un solo baricentro.
– Divide a cada mediana en relación como 1 es a 2.
– El baricentro es siempre un punto interior.
– Es llamado también gravicentro o centro de gravedad de la
región triangular.

6. Bisectriz
• Segmento que divide a un ángulo interior o
exterior en dos ángulos de igual medida.

7. Incentro
• Es el punto donde se intersectan las tres bisectrices
interiores de un triángulo.
• PARA RECORDAR
– Todo triángulo tiene un solo incentro.
– El incentro equidista de los lados del triángulo.
– El incentro es siempre un punto interior al triángulo.

8. Excentro
• Es el punto donde se intersectan dos bisectrices
exteriores con una bisectriz interior en un triángulo.
• PARA RECORDAR
– Todo triángulo tiene tres excentros.
– Los excentros son siempre puntos
– exteriores al triángulo.

9. Mediatriz
• Es una recta que pasa por el punto medio de
un lado cortándolo en forma perpendicular.

10. Circuncentro
• Es el punto donde se cortan las tres
mediatrices de un triángulo.
• C: Circuncentro

11. PARA RECORDAR
• Todo triángulo tiene un solo circuncentro.
• El circuncentro equidista de los vértices del triángulo.
• Es un punto interior si el triángulo es acutángulo.
• Es un punto exterior si el triángulo es obtusángulo.
• Si es rectángulo está en el punto medio de la
hipotenusa.

12. • Propiedad
• Si: "O" es circuncentro

13. Ceviana
• Segmento que une un vértice con un punto
cualquiera del lado opuesto o de su
prolongación.

14. Cevacentro
• Es el punto donde se intersectan tres cevianas de
un triángulo.
• C: Cevacentro o punto ceviano
• PARA RECORDAR
• Todo triángulo tiene infinitos cevacentros.

15. Observaciones
• Para ubicar un punto notable sólo es necesario trazar
dos líneas notables de la misma especie.
• En todos los triángulos isósceles, si se traza una de las
cuatro primeras líneas notables hacia la base, dicha
línea cumple las mismas funciones que las otras.
• En todo triángulo equilátero el ortocentro, baricentro,
incentro y circuncentro coinciden.
• En todo triángulo isósceles, el ortocentro, baricentro,
incentro y el excentro relativo a la base, se encuentran
alineados en la mediatriz de la base.

16. Propiedades con líneas notables
• Ángulo formado por dos bisectrices interiores.
• Ángulo formado por dos bisectrices exteriores

17. • Ángulo formado por una bisectriz interior y
una bisectriz exterior.