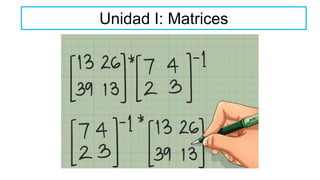
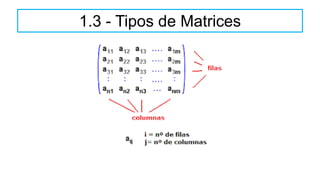
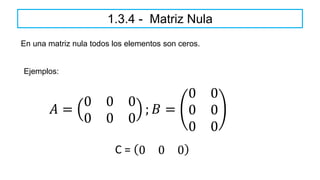
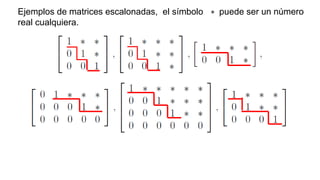
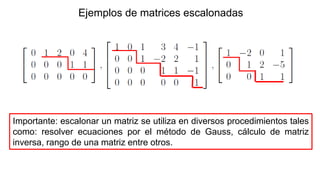
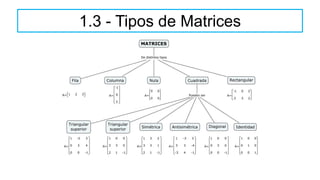
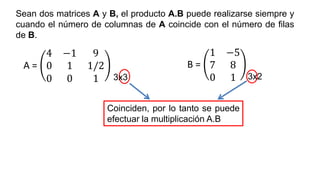
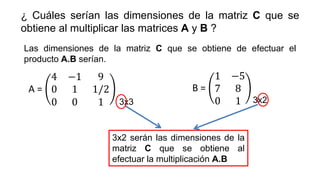
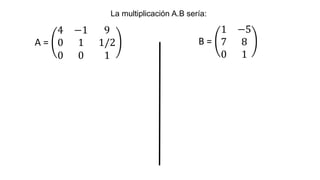
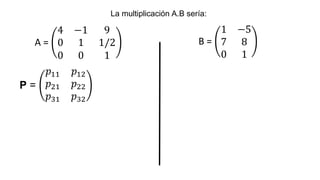
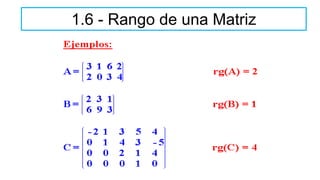
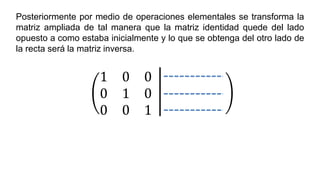
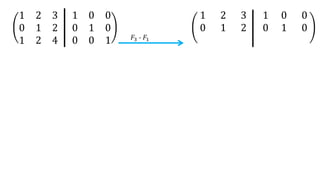
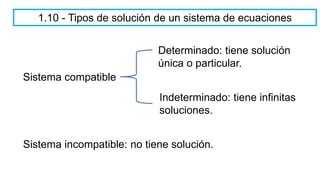
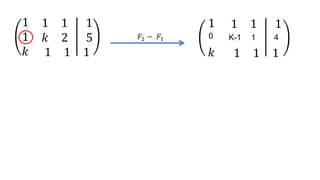
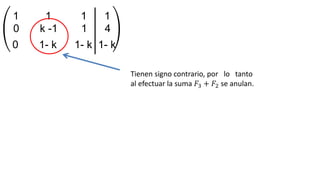
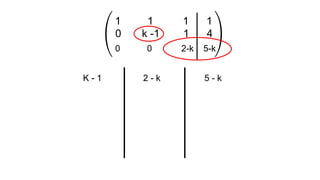
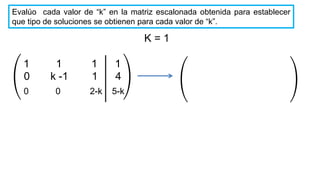
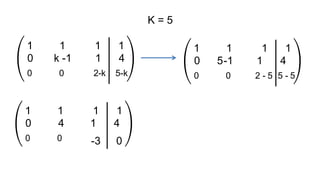
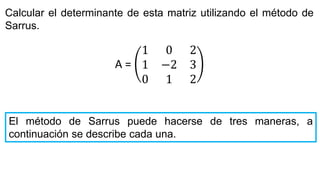
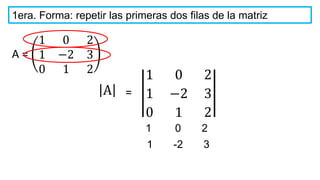
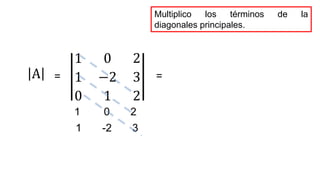
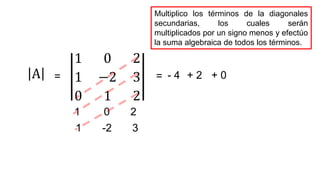
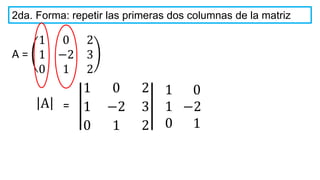
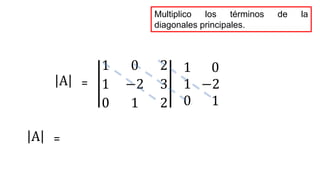
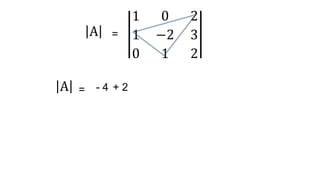
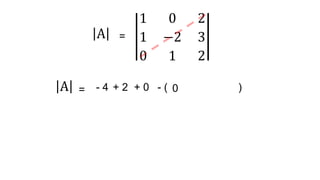
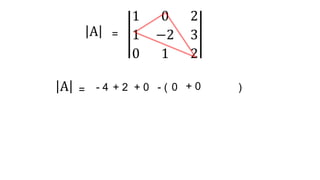
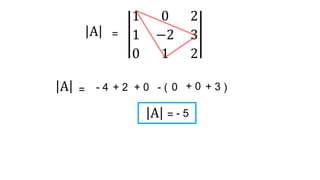
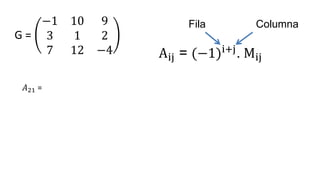
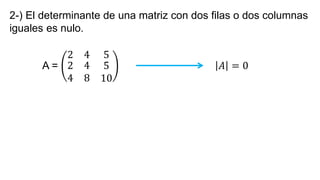
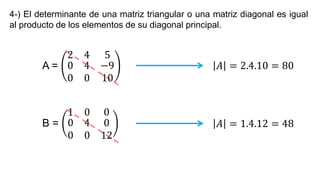
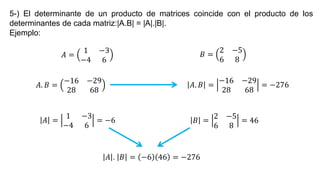
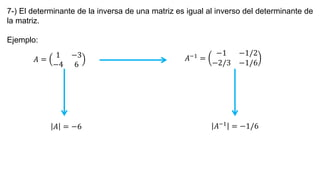
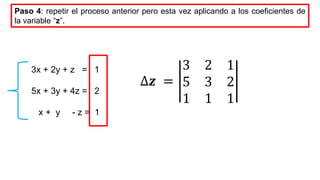
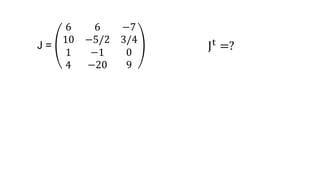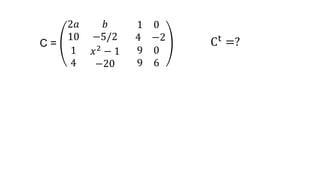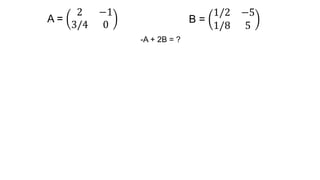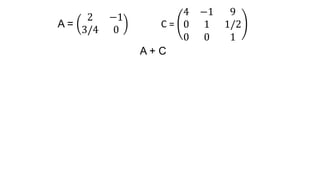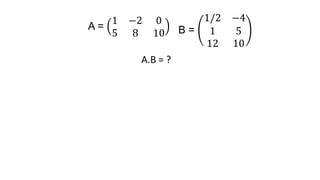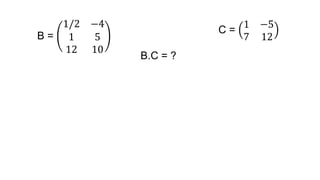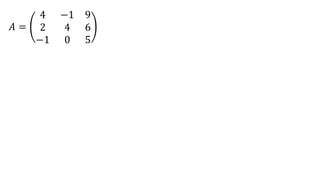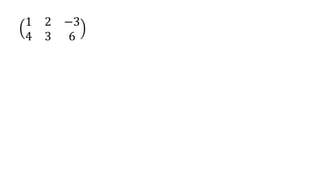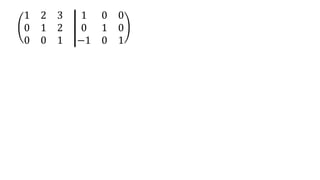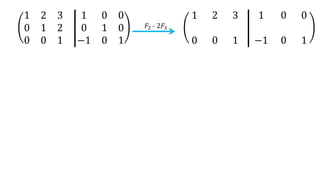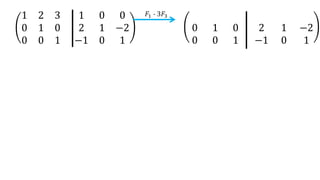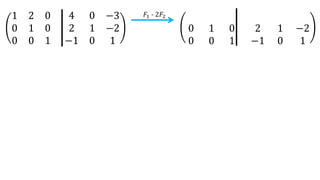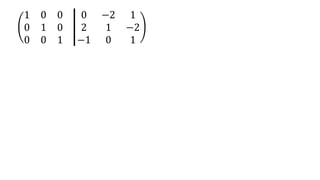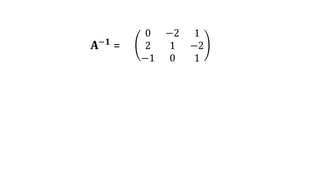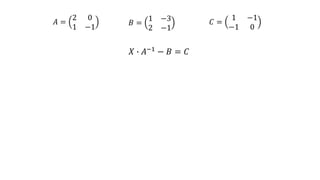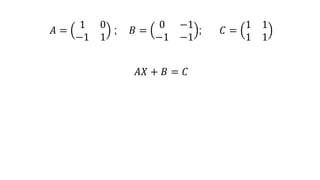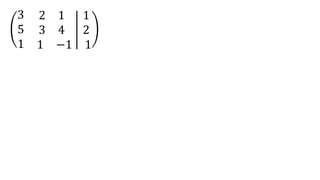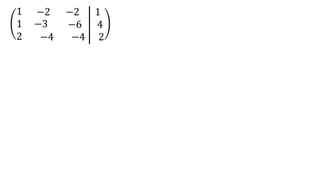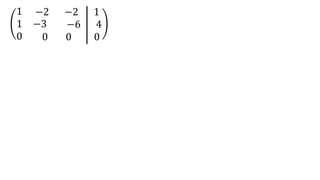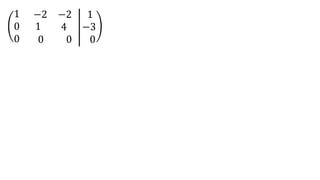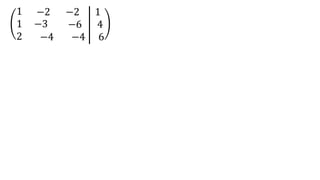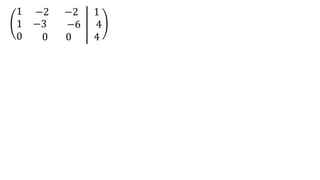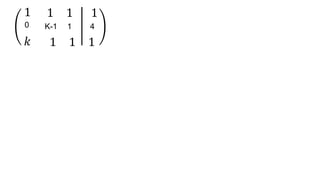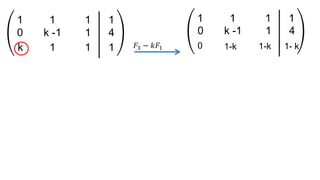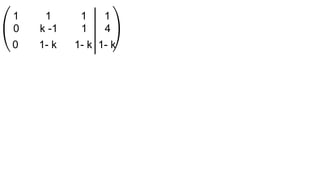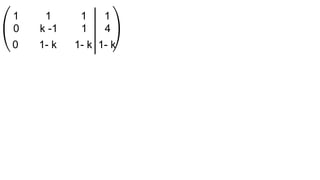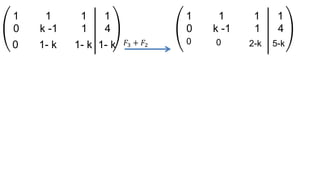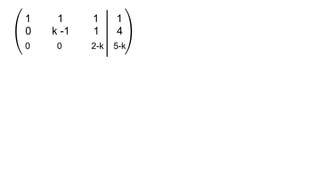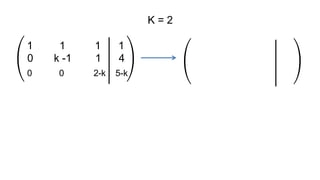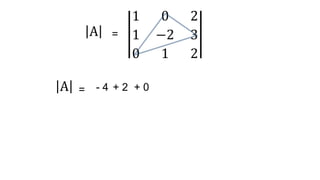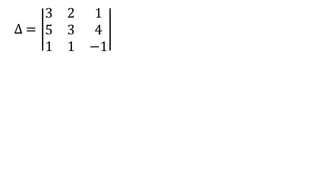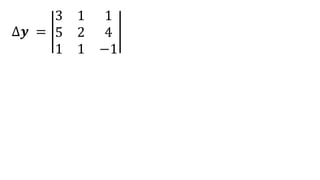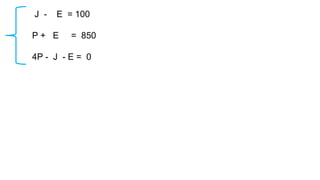El documento aborda el concepto de matrices, explicando su definición, orden, tipos y operaciones básicas como suma y multiplicación. Se detallan diferentes tipos de matrices, incluyendo matrices nulas, diagonales, identidad, simétricas, antisimétricas y escalonadas. También se introduce el método de Gauss para escalar matrices y calcular su rango.