1) Se define una matriz como un conjunto rectangular de elementos dispuestos en filas y columnas.
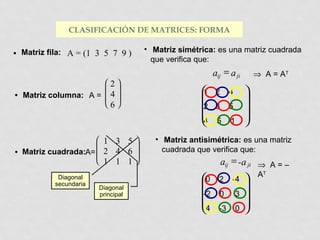
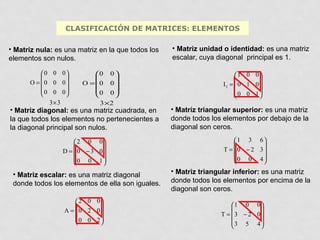
2) Se describen diferentes tipos de matrices como matrices cuadradas, simétricas, triangulares, etc. según la disposición de sus elementos.
3) Se explican diversas operaciones con matrices como suma, multiplicación por un escalar, producto y trasposición, así como algunas de sus propiedades.