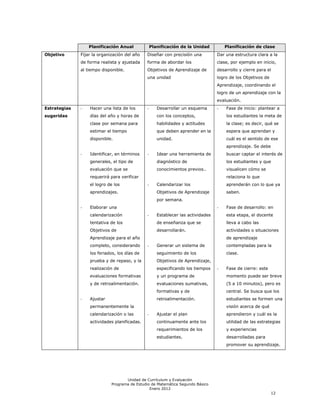
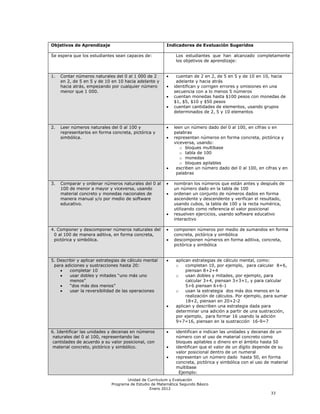
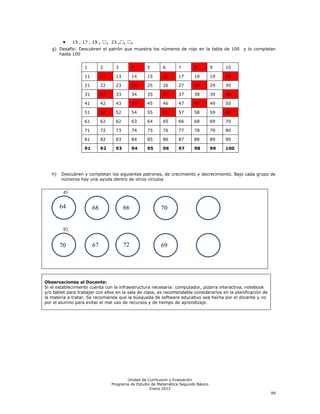
Este documento presenta el programa de estudio de matemáticas para segundo básico. Incluye una introducción sobre los objetivos de aprendizaje y nociones básicas del currículum. Luego, entrega orientaciones para la implementación del programa, con énfasis en el desarrollo del lenguaje. Finalmente, describe el contenido del programa dividido en unidades para cada semestre.