Fisica general para leer

F¶³sica General
Ignacio Mart¶³n Bragado
imartin@ele.uva.es
2 de febrero de 2004

2 (C) Ignacio Mart¶³n Bragado. imartin@ele.uva.es

¶Indice general
1. Distribuci¶on de este documento 11
2. Introducci¶on 13
2.1. Signos empleados . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 13
3. Esquema 15
4. Introducci¶on al c¶alculo vectorial 17
4.1. Magnitudes escalares y vectoriales . . . . . . . . . . . . . . . . . . . 17
4.1.1. Representaci¶on matem¶atica . . . . . . . . . . . . . . . . . . . 17
4.2. Operaciones vectoriales unarias . . . . . . . . . . . . . . . . . . . . . 17
4.2.1. Operaciones unarias diferenciales . . . . . . . . . . . . . . . . 18
4.3. Operaciones vectoriales binarias . . . . . . . . . . . . . . . . . . . . . 18
4.3.1. Equivalencia . . . . . . . . . . . . . . . . . . . . . . . . . . . 18
4.3.2. Suma y resta . . . . . . . . . . . . . . . . . . . . . . . . . . . 18
4.3.3. Producto escalar . . . . . . . . . . . . . . . . . . . . . . . . . 19
4.3.4. Producto vectorial . . . . . . . . . . . . . . . . . . . . . . . . 19
4.3.5. Producto mixto . . . . . . . . . . . . . . . . . . . . . . . . . . 21
5. Cinem¶atica 23
5.1. Introducci¶on . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 23
5.2. Velocidad . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 23
5.3. Aceleraci¶on . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 24
5.4. Componentes intr¶³nsecas de la aceleraci¶on . . . . . . . . . . . . . . . 24
5.5. Clasi¯caci¶on de movimientos . . . . . . . . . . . . . . . . . . . . . . 25
5.6. Composici¶on de movimientos . . . . . . . . . . . . . . . . . . . . . . 25
5.6.1. Translaci¶on pura . . . . . . . . . . . . . . . . . . . . . . . . . 25
5.6.2. Rotaci¶on pura . . . . . . . . . . . . . . . . . . . . . . . . . . 26
5.7. Resoluci¶on de problemas . . . . . . . . . . . . . . . . . . . . . . . . . 27
5.7.1. Tiro parab¶olico . . . . . . . . . . . . . . . . . . . . . . . . . . 27
5.7.2. Componentes intr¶³nsecas . . . . . . . . . . . . . . . . . . . . . 27
5.7.3. C¶alculo de trayectorias . . . . . . . . . . . . . . . . . . . . . . 28
6. Din¶amica 29
6.1. Introducci¶on . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 29
6.2. Leyes de Newton . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 29
6.2.1. Ley de la inercia . . . . . . . . . . . . . . . . . . . . . . . . . 29
6.2.2. Segunda ley de Newton . . . . . . . . . . . . . . . . . . . . . 29
6.2.3. Tercera ley de Newton . . . . . . . . . . . . . . . . . . . . . . 30
6.3. Fuerzas especiales que aparecen en problemas . . . . . . . . . . . . . 30
6.3.1. Normal . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 30
6.3.2. Rozamiento . . . . . . . . . . . . . . . . . . . . . . . . . . . . 31
3

¶INDICE GENERAL
6.4. El momento lineal . . . . . . . . . . . . . . . . . . . . . . . . . . . . 32
6.4.1. Conservaci¶on del momento lineal . . . . . . . . . . . . . . . . 32
6.5. Conservaci¶on de la energ¶³a . . . . . . . . . . . . . . . . . . . . . . . . 33
6.6. Resoluci¶on de problemas . . . . . . . . . . . . . . . . . . . . . . . . . 33
6.6.1. Planos inclinados . . . . . . . . . . . . . . . . . . . . . . . . . 33
6.6.2. Curvas . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 35
6.6.3. Casos l¶³mite . . . . . . . . . . . . . . . . . . . . . . . . . . . . 36
7. Consideraciones energ¶eticas 39
7.1. Introducci¶on . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 39
7.2. Trabajo . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 39
7.2.1. Trabajo conservativo . . . . . . . . . . . . . . . . . . . . . . . 40
7.3. Potencia . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 40
7.4. Energ¶³a . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 41
7.5. Conceptos previos . . . . . . . . . . . . . . . . . . . . . . . . . . . . 41
7.5.1. Energ¶³a cin¶etica . . . . . . . . . . . . . . . . . . . . . . . . . 41
7.5.2. Potencial . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 43
7.6. Conservaci¶on de la energ¶³a . . . . . . . . . . . . . . . . . . . . . . . . 45
7.6.1. Rozamiento . . . . . . . . . . . . . . . . . . . . . . . . . . . . 45
7.7. Impulso . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 47
7.8. Gradiente . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 47
8. Din¶amica de un sistema de part¶³culas 49
8.1. Conceptos y de¯niciones primarias . . . . . . . . . . . . . . . . . . . 49
8.2. Centro de masas . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 49
8.2.1. Teorema de Pappus . . . . . . . . . . . . . . . . . . . . . . . 49
8.3. Din¶amica del centro de masas . . . . . . . . . . . . . . . . . . . . . . 50
8.3.1. Velocidad . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 50
8.3.2. Aceleraci¶on . . . . . . . . . . . . . . . . . . . . . . . . . . . . 50
8.3.3. Momento lineal . . . . . . . . . . . . . . . . . . . . . . . . . . 50
8.3.4. Energ¶³a . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 50
8.4. Aplicaciones . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 51
8.4.1. Sistema de referencia del centro de masas . . . . . . . . . . . 51
8.4.2. Problemas de dos cuerpos . . . . . . . . . . . . . . . . . . . . 52
8.4.3. Colisiones . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 52
9. Din¶amica de la rotaci¶on 53
9.1. Introducci¶on . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 53
9.1.1. S¶olido r¶³gido . . . . . . . . . . . . . . . . . . . . . . . . . . . 53
9.1.2. Analog¶³as . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 53
9.2. Momento de una fuerza . . . . . . . . . . . . . . . . . . . . . . . . . 53
9.3. Momento angular . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 54
9.4. Momento de inercia . . . . . . . . . . . . . . . . . . . . . . . . . . . 55
9.4.1. Teorema de Steiner o de los ejes paralelos . . . . . . . . . . . 55
9.4.2. Teorema de las ¯guras planas o de los ejes perpendiculares. . 56
9.4.3. Relaci¶on del momento de inercia respecto a un punto con los
tres ejes . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 56
9.5. Ecuaci¶on de la din¶amica de rotaci¶on . . . . . . . . . . . . . . . . . . 56
9.5.1. Conservaci¶on del momento angular . . . . . . . . . . . . . . . 57
9.6. Energ¶³a de rotaci¶on . . . . . . . . . . . . . . . . . . . . . . . . . . . . 57
9.7. Algunos problemas t¶³picos de rotaci¶on . . . . . . . . . . . . . . . . . 57
9.7.1. Cuerpos rodantes . . . . . . . . . . . . . . . . . . . . . . . . . 58
9.7.2. Poleas . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 58
9.7.3. Est¶atica y equilibrios . . . . . . . . . . . . . . . . . . . . . . . 58

¶INDICE GENERAL
9.7.4. C¶alculo de la aceleraci¶on angular de un cuerpo . . . . . . . . 59
9.7.5. C¶alculo de momentos de inercia . . . . . . . . . . . . . . . . . 59
9.7.6. Variaci¶on de la forma del cuerpo que gira . . . . . . . . . . . 59
9.7.7. Conservaci¶on de la energ¶³a para cuerpos rodantes . . . . . . . 60
10.Conceptos generales de campos 61
10.1. Introducci¶on . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 61
10.2. De¯nici¶on . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 61
10.3. Formalismo matem¶atico . . . . . . . . . . . . . . . . . . . . . . . . . 61
10.4. Flujo de un campo vectorial . . . . . . . . . . . . . . . . . . . . . . . 62
10.5. Gradiente de un campo . . . . . . . . . . . . . . . . . . . . . . . . . 62
10.6. Ley de Gauss . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 62
10.7. Circulaci¶on . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 63
10.8. Representaci¶on gr¶a¯ca de los campos . . . . . . . . . . . . . . . . . . 63
10.8.1. Campo escalar . . . . . . . . . . . . . . . . . . . . . . . . . . 63
10.8.2. Campo vectorial . . . . . . . . . . . . . . . . . . . . . . . . . 64
11.Gravitaci¶on y campo gravitatorio 65
11.1. Introducci¶on . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 65
11.2. Ley de la gravitaci¶on universal . . . . . . . . . . . . . . . . . . . . . 65
11.2.1. Enunciado . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 65
11.2.2. Las leyes de Kepler . . . . . . . . . . . . . . . . . . . . . . . . 66
11.2.3. Principio de superposici¶on . . . . . . . . . . . . . . . . . . . . 66
11.3. Campo gravitatorio . . . . . . . . . . . . . . . . . . . . . . . . . . . . 66
11.3.1. Concepto . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 66
11.3.2. Entidad matem¶atica . . . . . . . . . . . . . . . . . . . . . . . 67
11.4. Energ¶³a potencial gravitatoria . . . . . . . . . . . . . . . . . . . . . . 67
11.5. Problemas concretos . . . . . . . . . . . . . . . . . . . . . . . . . . . 69
11.5.1. C¶alculo de la fuerza gravitatoria ejercida por un sistema de
part¶³culas . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 69
11.5.2. C¶alculo de la fuerza gravitatoria ejercida por un cuerpo continuo 69
11.5.3. Problemas de sat¶elites . . . . . . . . . . . . . . . . . . . . . . 69
11.5.4. Velocidad de escape . . . . . . . . . . . . . . . . . . . . . . . 69
11.5.5. Medida de la gravedad en la super¯cie de un planeta . . . . . 70
11.5.6. C¶alculo de la atracci¶on gravitatoria de algunos s¶olidos simples 70
12.Campo y potencial el¶ectrico 73
12.1. Preliminar . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 73
12.2. Ley de Coulomb . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 73
12.2.1. Principio de superposici¶on . . . . . . . . . . . . . . . . . . . . 73
12.3. Campo el¶ectrico . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 73
12.4. Ley de Gauss . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 74
12.5. Potencial y energ¶³a el¶ectrica . . . . . . . . . . . . . . . . . . . . . . . 74
12.5.1. Algunos casos particulares de potencial el¶ectrico . . . . . . . 75
12.6. Condensadores . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 75
12.6.1. Asociaci¶on de condensadores . . . . . . . . . . . . . . . . . . 75
13.Movimiento arm¶onico simple 77
13.1. Introducci¶on . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 77
13.2. Din¶amica del sistema . . . . . . . . . . . . . . . . . . . . . . . . . . . 77
13.2.1. Ecuaci¶on del movimiento . . . . . . . . . . . . . . . . . . . . 77
13.2.2. Periodicidad de la ecuaci¶on . . . . . . . . . . . . . . . . . . . 78
13.2.3. Velocidad . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 78
13.2.4. Aceleraci¶on . . . . . . . . . . . . . . . . . . . . . . . . . . . . 79
F¶³sica General. http://www.ele.uva.es/~imartin/libro/index.html 5

¶INDICE GENERAL
13.3. Energ¶³a . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 79
13.3.1. Energ¶³a cin¶etica . . . . . . . . . . . . . . . . . . . . . . . . . 79
13.3.2. Energ¶³a potencial . . . . . . . . . . . . . . . . . . . . . . . . . 79
13.3.3. Energ¶³a mec¶anica . . . . . . . . . . . . . . . . . . . . . . . . . 80
13.4. El p¶endulo simple . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 80
14.Ondas 83
14.1. Introducci¶on . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 83
14.1.1. Tipos de ondas . . . . . . . . . . . . . . . . . . . . . . . . . . 83
14.2. Ecuaci¶on general de una onda . . . . . . . . . . . . . . . . . . . . . . 84
14.3. Ecuaci¶on de una onda arm¶onica . . . . . . . . . . . . . . . . . . . . . 84
14.3.1. Periodo y frecuencia . . . . . . . . . . . . . . . . . . . . . . . 85
14.3.2. Longitud de onda y n¶umero de ondas . . . . . . . . . . . . . 85
14.4. Consideraciones energ¶eticas de las ondas . . . . . . . . . . . . . . . . 87
14.4.1. Energ¶³a . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 87
14.4.2. Potencia . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 88
14.4.3. Intensidad . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 88
15.Fen¶omenos ondulatorios 89
15.1. Introducci¶on . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 89
15.2. Principio de Huygens . . . . . . . . . . . . . . . . . . . . . . . . . . . 89
15.3. Interferencia entre ondas . . . . . . . . . . . . . . . . . . . . . . . . . 89
15.3.1. Ondas coherentes: Interferencias constructivas y destructivas 90
15.3.2. Ondas estacionarias: Propagaci¶on en direcciones opuestas . . 93
15.4. Otras propiedades de las ondas . . . . . . . . . . . . . . . . . . . . . 95
15.4.1. Difracci¶on . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 95
15.4.2. Polarizaci¶on . . . . . . . . . . . . . . . . . . . . . . . . . . . . 95
15.4.3. Otras propiedades . . . . . . . . . . . . . . . . . . . . . . . . 96
15.5. Re°exi¶on y refracci¶on de la luz . . . . . . . . . . . . . . . . . . . . . 96
15.5.1. Re°exi¶on . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 96
15.5.2. Refracci¶on . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 97
15.5.3. Principio de Fermat . . . . . . . . . . . . . . . . . . . . . . . 99
16.Electromagnetismo 101
16.1. Introducci¶on . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 101
16.2. Fuerza de Lorentz . . . . . . . . . . . . . . . . . . . . . . . . . . . . 101
16.2.1. Fuerza sobre una corriente el¶ectrica . . . . . . . . . . . . . . 102
16.3. Campo magn¶etico debido a una carga en movimiento . . . . . . . . . 102
16.3.1. Campo magn¶etico producido por una corriente el¶ectrica . . . 103
16.4. Ley de Ampµere . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 103
16.5. Resoluci¶on de problemas t¶³picos . . . . . . . . . . . . . . . . . . . . . 104
16.5.1. Part¶³cula sometida a un campo magn¶etico constante y uniforme104
16.5.2. Fuerza magn¶etica experimentada por un conductor recto y
perpendicular al campo magn¶etico . . . . . . . . . . . . . . . 104
16.5.3. Campo magn¶etico creado por un conductor recto e in¯nito . 104
16.5.4. Campo producido por una espira en su eje . . . . . . . . . . . 105
16.5.5. Campo magn¶etico en el interior de un solenoide in¯nito . . . 106
16.5.6. Fuerzas entre corrientes paralelas . . . . . . . . . . . . . . . . 107
17.Inducci¶on electromagn¶etica 109
17.1. Introducci¶on . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 109
17.2. Ley de Faraday-Henry . . . . . . . . . . . . . . . . . . . . . . . . . . 109
17.2.1. Ley de Lenz . . . . . . . . . . . . . . . . . . . . . . . . . . . . 110
17.3. Fuerza electromotriz . . . . . . . . . . . . . . . . . . . . . . . . . . . 110

¶INDICE GENERAL
17.4. Autoinducci¶on . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 110
17.4.1. Inducci¶on mutua . . . . . . . . . . . . . . . . . . . . . . . . . 111
17.5. Energ¶³a magn¶etica . . . . . . . . . . . . . . . . . . . . . . . . . . . . 111
17.6. Problemas y aplicaciones de inducci¶on electromagn¶etica . . . . . . . 112
17.6.1. Generadores . . . . . . . . . . . . . . . . . . . . . . . . . . . . 112
17.6.2. Transformadores . . . . . . . . . . . . . . . . . . . . . . . . . 113
17.6.3. Autoinducci¶on de un solenoide . . . . . . . . . . . . . . . . . 114
18.La naturaleza de la luz. Dualidad onda corp¶usculo de la materia 115
18.1. Introducci¶on hist¶orica . . . . . . . . . . . . . . . . . . . . . . . . . . 115
18.2. El cuerpo negro . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 116
18.3. El efecto fotoel¶ectrico . . . . . . . . . . . . . . . . . . . . . . . . . . 117
18.3.1. Descripci¶on del problema . . . . . . . . . . . . . . . . . . . . 117
18.3.2. Soluci¶on . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 118
18.4. Efecto Compton . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 119
18.5. Naturaleza ondulatoria de la materia . . . . . . . . . . . . . . . . . . 119
18.6. Resumen: Dualidad onda-corp¶usculo de la luz y la materia . . . . . . 120
19.Fundamentos de F¶³sica Nuclear 123
19.1. Introducci¶on . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 123
19.2. El n¶ucleo at¶omico . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 123
19.2.1. Algunas de¯niciones . . . . . . . . . . . . . . . . . . . . . . . 123
19.2.2. Caracter¶³sticas . . . . . . . . . . . . . . . . . . . . . . . . . . 124
19.3. Radiactividad . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 124
19.3.1. Radiactividad ® . . . . . . . . . . . . . . . . . . . . . . . . . 125
19.3.2. Radiactividad ¯ . . . . . . . . . . . . . . . . . . . . . . . . . 125
19.3.3. Radiactividad ° . . . . . . . . . . . . . . . . . . . . . . . . . 125
19.4. Caracter¶³sticas de los procesos radiactivos . . . . . . . . . . . . . . . 126
19.4.1. Cin¶etica de las reacciones nucleares: Ley de desintegraci¶on . . 126
19.4.2. Las series radiactivas . . . . . . . . . . . . . . . . . . . . . . . 126
19.5. Reacciones nucleares . . . . . . . . . . . . . . . . . . . . . . . . . . . 128
19.5.1. Fisi¶on nuclear . . . . . . . . . . . . . . . . . . . . . . . . . . . 128
19.5.2. Fusi¶on nuclear . . . . . . . . . . . . . . . . . . . . . . . . . . 129
A. Esquemas y formulario 131
A.1. C¶alculo vectorial . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 131
A.2. Cinem¶atica . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 131
A.2.1. Movimiento circular . . . . . . . . . . . . . . . . . . . . . . . 132
A.3. Din¶amica . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 132
A.3.1. Translaci¶on . . . . . . . . . . . . . . . . . . . . . . . . . . . . 132
A.3.2. Rotaci¶on . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 132
A.4. Trabajo y Energ¶³a . . . . . . . . . . . . . . . . . . . . . . . . . . . . 133
A.5. Movimiento arm¶onico simple . . . . . . . . . . . . . . . . . . . . . . 133
A.6. Campo y potencial el¶ectrico y gravitatorio . . . . . . . . . . . . . . . 134
A.7. Circuitos de corriente continua . . . . . . . . . . . . . . . . . . . . . 135
A.8. Electromagnetismo . . . . . . . . . . . . . . . . . . . . . . . . . . . . 135
B. Movimiento de un cuerpo en el campo gravitatorio bajo el roza-miento
con el aire 137
B.1. Introducci¶on . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 137
B.2. Planteamiento de la ley de Newton . . . . . . . . . . . . . . . . . . . 137
B.3. Interpretaci¶on de la ecuaci¶on de Newton . . . . . . . . . . . . . . . . 137
B.4. Conclusi¶on . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 138

¶INDICE GENERAL
C. Tablas y f¶ormulas ¶utiles 139
C.1. Introducci¶on . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 139
C.2. C¶alculo complejo . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 139
C.3. C¶alculo vectorial . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 139
C.4. Funciones elementales . . . . . . . . . . . . . . . . . . . . . . . . . . 139
C.4.1. Trigonom¶etricas . . . . . . . . . . . . . . . . . . . . . . . . . 139
C.4.2. Logar¶³tmicas y exponenciales . . . . . . . . . . . . . . . . . . 140
C.5. Derivaci¶on . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 140
C.5.1. Propiedades generales . . . . . . . . . . . . . . . . . . . . . . 140
C.5.2. Tabla de derivadas . . . . . . . . . . . . . . . . . . . . . . . . 140
C.6. Integraci¶on . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 140
C.6.1. De¯nici¶on y propiedades . . . . . . . . . . . . . . . . . . . . . 140
C.6.2. Tabla de integrales . . . . . . . . . . . . . . . . . . . . . . . . 141
D. Agradecimientos 143
Bibliograf¶³a 144

¶Indice de ¯guras
4.1. El ¶angulo entre dos vectores y sus proyecciones. . . . . . . . . . . . . 21
5.1. Relaci¶on vectorial entre unos y otros sistemas. El conductor ver¶a la
piedra que cae como ~rcp = ~rc ¡~rp. . . . . . . . . . . . . . . . . . . . 26
6.1. Descomposici¶on de las fuerzas en un plano inclinado. . . . . . . . . . 33
6.2. >Cu¶al ser¶a la aceleraci¶on de este sistema? . . . . . . . . . . . . . . . 34
6.3. Distintas situaciones ante una curva. . . . . . . . . . . . . . . . . . . 36
6.4. >Desde qu¶e altura podr¶a una masa realizar un bucle?. . . . . . . . . 37
7.1. >A qu¶e velocidad llegar¶a al ¯nal?. . . . . . . . . . . . . . . . . . . . . 46
9.1. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 56
11.1. Campo ~g generado por una varilla delgada. . . . . . . . . . . . . . . 70
12.1. Asociaci¶on de condensadores en serie y en paralelo. . . . . . . . . . . 75
13.1. Descomposici¶on de las fuerzas en un p¶endulo. . . . . . . . . . . . . . 81
14.1. Periodo de una onda arm¶onica. . . . . . . . . . . . . . . . . . . . . . 86
14.2. Longitud de onda de una onda arm¶onica. . . . . . . . . . . . . . . . 87
15.1. Esquema de un fen¶omeno de interferencias. . . . . . . . . . . . . . . 90
15.2. Representaci¶on de una interferencia (casi) constructiva. . . . . . . . 91
15.3. Representaci¶on de una interferencia destructiva. . . . . . . . . . . . . 92
15.4. Experiencia de Young. . . . . . . . . . . . . . . . . . . . . . . . . . . 93
15.5. Re°exi¶on de una onda. . . . . . . . . . . . . . . . . . . . . . . . . . . 97
15.6. Explicaci¶on seg¶un el principio de Huygens de la re°exi¶on. . . . . . . 97
15.7. Refracci¶on de una onda. . . . . . . . . . . . . . . . . . . . . . . . . . 98
15.8. Explicaci¶on seg¶un el principio de Huygens de la refracci¶on. . . . . . 98
16.1. Geometr¶³a para calcular el campo magn¶etico en el eje de una espira. 105
16.2. Trayectoria para un solenoide in¯nito. . . . . . . . . . . . . . . . . . 106
17.1. Circuito con una resistencia y una autoinducci¶on. . . . . . . . . . . . 111
17.2. Corriente alterna. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 113
17.3. Esquema simpli¯cado de un transformador. . . . . . . . . . . . . . . 114
18.1. Dibujo de un cuerpo negro". . . . . . . . . . . . . . . . . . . . . . . 116
18.2. Distribuci¶on espectral de la radiaci¶on emitida por un cuerpo negro a
distintas temperaturas. . . . . . . . . . . . . . . . . . . . . . . . . . . 116
18.3. Dispositivo simpli¯cado para la medici¶on del efecto fotoel¶ectrico. . . 118
9

¶INDICE DE FIGURAS
19.1. Serie radiactiva del uranio. . . . . . . . . . . . . . . . . . . . . . . . 127

Cap¶³tulo 1
Distribuci¶on de este
documento
Este libro ha sido escrito ¶³ntegramente por Ignacio Mart¶³n Bragado y todo su
material es original, incluyendo los gr¶a¯cos que contiene, excepto los iconos de am-pliaci
¶on, recuerda, nota, problema y resoluci¶on que han sido tomados del proyecto
GNOME (distribuido con licencia GPL) y modi¯cados. Ha sido compuesto utilizan-do
LATEXsobre un ordenador AMD K6 utilizando un sistema operativo GNU/Linux.
Se permite la reproducci¶on de los contenidos de este libro siempre y cuando
quede absolutamente expl¶³cita la procedencia de este documento y su autor y se
conserve esta leyenda.
No se permite la modi¯caci¶on de ning¶un t¶opico de este libro. Si desea reali-zar
alguna correcci¶on h¶agalo poni¶endose en contacto con el autor en la direcci¶on
imartin@ele.uva.es
La direcci¶on web original de este material es:
http://www.ele.uva.es/~imartin/libro/index.html
11

CAP¶ITULO 1. DISTRIBUCI¶ON DE ESTE DOCUMENTO

Cap¶³tulo 2
Introducci¶on
Este esquema pretende ser una peque~na gu¶³a para resolver los problemas de
f¶³sica evitando las confusiones m¶as usuales. No obstante no existe un sistema que
resuelva los problemas de f¶³sica, sino que, cada uno, presenta una faceta que hemos
de descubrir haciendo uso de nuestra raz¶on.
Este esquema no pretende ser un chuletario de los distintos tipos de problemas y
como solucionarlos, sino s¶olo una iniciaci¶on b¶asica en el arte de resolver" problemas
de f¶³sica.
El planteamiento de las ecuaciones que intervienen en los procesos f¶³sicos es, a
nivel general, algo complicado, puesto que son muchos los fen¶omenos que pueden
presentarse. En esta gu¶³a iremos desgajando los distintos procesos que pueden darse
y las ecuaciones involucradas.
La creaci¶on de este esquema ha sido un proceso complicado. Inicialmente cons-tituy
¶o unos breves apuntes que se impart¶³an para un curso del (extinto o en v¶³as
de extinci¶on) COU, pero se fueron a~nadiendo cosas y mezclando parte de los con-tenidos
b¶asicos de dicho curso con algunas consideraciones de ¶³ndole m¶as pr¶actica
fruto de la experiencia en el aula.
Actualmente el nivel de este libro hace que pueda ser utilizado para la asigna-tura
de F¶³sica de 1o de las carreras de ciencias. Para 2o de Bachillerato quiz¶as su
nivel exceda un poco en algunos temas y no contenga otros. En cualquier caso la
concepci¶on ¯nal de este libro es como Curso de f¶³sica general" y no como un libro
de texto de ning¶un curso espec¶³¯co de Facultad ni Instituto.
2.1. Signos empleados
¦ Cuando aparezca alg¶un comentario de inter¶es, si bien no sea importante Nota
para el desarrollo del tema, se tratar¶a de esta manera.
± Las partes del desarrollo que excedan un poco los objetivos de este libro,
pero no por ello dejen de ser interesantes o importantes aparecera¶n de esta Ampliacio¶n
manera.
. Aquellos p¶arrafos que sean muy importantes o que sea conveniente
Recuerda
recordar, ya que pueden constituir alg¶un dato esencial o un resumen de
todo lo dicho se indicar¶an de esta forma.
P El enunciado de algunos problemas que sean posteriormente re- Problema
sueltos.
13

CAP¶ITULO 2. INTRODUCCI¶ON
R La resoluci¶on del problema con los c¶alculos y explicaciones perti-nentes.
Resolucio¶n

Cap¶³tulo 3
Esquema
Para plantear un problema de f¶³sica se pueden seguir los siguientes pasos:
Hacer un dibujo explicativo. Esto supone haber le¶³do antes bien el enunciado
comprendiendo exactamente qu¶e datos se ofrecen y qu¶e resultados se piden.
Elegir un sistema de coordenadas adecuado, que ser¶a aquel que nos facilite
la posterior resoluci¶on del problema. Hay que ser coherente con el sistema de
coordenadas que se elija, re¯riendo posteriormente a ¶el todas las cantidades
con sus correspondientes signos.
La elecci¶on de un sistema de coordenadas no siempre es ¶unica, pero en cual-quier
caso hay que hacer una que otorgue sencillez al problema, por coincidir,
generalmente, con alg¶un punto particular que pueda dar posteriormente m¶as
simplicidad al planteamiento o a los c¶alculos.
Comprobar las fuerzas que intervienen en el problema. Suelen ser siempre
menos de las que parecen. Sobre todo no hay que olvidar la fuerza de gravedad,
de rozamiento, posibles tensiones, fuerzas el¶asticas1 as¶³ como sus reacciones.
Considerar las proyecciones sobre los ejes. Una vez comprobadas las fuerzas
que intervienen en el problema habr¶a que proyectarlas sobre los ejes del sis-tema
de coordenadas, para poder as¶³ darlas un tratamiento vectorial. Esta
proyecci¶on es m¶as sencilla de lo que suele parecer. Basta recordar las relacio-nes
sin ® y cos ®.
Plantear las ecuaciones para cada eje. Pueden ser ecuaciones din¶amicas del
tipo
P
F = ma o cinem¶aticas. Hay que ser conscientes de que la ¶unica f¶ormu-la"
que se suele emplear es
P ~F = m~a, pero que, como ¶esta es una ecuaci¶on
vectorial, se descompone en tantas ecuaciones como dimensiones tenga el mo-vimiento,
o lo que es lo mismo, en tantas proyecciones como ejes tenga nuestro
sistema de coordenadas elegido.
Como en pasos anteriores ya hemos considerado las fuerzas que intervienen
y sus proyecciones este paso no debe ser sino un recuento cuidadoso de las
fuerzas que aparecen en un determinado eje o direcci¶on lig¶andolas con la
ecuaci¶on correspondiente.
Este paso es estudiado m¶as ampliamente en los cap¶³tulos siguientes.
Relacionar las ecuaciones planteadas con los datos que tenemos y los que que-remos
saber. Es decir, encontrar el sistema matem¶atico que nos lograr¶a en-contrar
la soluci¶on.
1Cuando hay muelles.
15

CAP¶ITULO 3. ESQUEMA
Resolver los sistemas matem¶aticos involucrados. ¶Este es un mero ejercicio
matem¶atico en el cual buscaremos la soluci¶on al problema.
Interpretar la soluci¶on. La interpretaci¶on de la soluci¶on consiste en mostrarse
cr¶³ticos hacia los resultados logrados, plante¶andose si estos son coherentes con
la intuici¶on, con lo que esper¶abamos que saliera, si responden bien al criterio
de signos y sistema de coordenadas elegido, si tienen un orden de magnitud2
apropiado y est¶an en las unidades oportunas, as¶³ como todo lo que nos parezca
oportuno indagar en nuestra propia soluci¶on.
En caso de que el resultado parezca correcto" lo cual, lamentablemente, no
quiere decir que lo sea, podremos dar por concluido el problema. En caso
contrario es conveniente volver a repasar todo el ejercicio, o la parte de la cual
nos mostremos insegura, para ver si detectamos alguna inconsistencia.
2Es decir, si no son demasiado grandes o peque~nos.

Cap¶³tulo 4
Introducci¶on al c¶alculo
vectorial
4.1. Magnitudes escalares y vectoriales
Llamamos magnitud escalar, o simplemente escalar, a toda magnitud que puede
expresarse simplemente con un ¶unico n¶umero. Por ejemplo, el peso o la altura de
una persona es una magnitud escalar.
Se denomina magnitud vectorial o vector a aquella medida para la cual nece-sitamos
dar algo m¶as que un s¶olo n¶umero". Por ejemplo, para saber la velocidad
del viento adem¶as de su intensidad, es decir, tantos kil¶ometros por hora, se requiere
conocer su direcci¶on y sentido, y as¶³ saber si viene del norte hacia el sur, etc. . . Este
tipo de magnitudes se denominan vectores.
4.1.1. Representaci¶on matem¶atica
Matem¶aticamente un escalar se representa con un ¶unico n¶umero1 y un vector
con una serie de coordenadas, tantas como dimensiones tenga el espacio en el que
se representa.
As¶³ un vector ~v se representa como
~v = (vx; vy; vz) = vx^{ + vy^| + vz^k;
siendo vx, vy y vz las componentes del vector, es decir, sus proyecciones sobre los
ejes x,y y z. A su vez ^{, ^| y ^k son los vectores unitarios en las direcciones de los ejes
x,y y z respectivamente.
4.2. Operaciones vectoriales unarias
Se llama m¶odulo de un vector a lo que ¶este mide". Se calcula como
j~vj = v =
q
v2x
y + v2
z : (4.1)
+ v2
Proyecci¶on de un vector sobre un eje es la sombra" de dicho vector sobre el eje
si la luz que proyecta dicha sombra" cayera justo perpendicularmente. As¶³ las
proyecciones de un vector ~v sobre los ejes x,y y z ser¶an vx, vy y vz respectivamente.
1Que normalmente pertenece al cuerpo de los n¶umeros reales
17

CAP¶ITULO 4. INTRODUCCI¶ON AL C¶ALCULO VECTORIAL
El inverso de un vector es dicho vector con sus proyecciones cambiadas de signo. La
suma de un vector y su inverso da siempre el vector nulo.
¡~v = (¡vx;¡vy;¡vz):
Vector nulo es aquel vector cuyo m¶odulo es cero. Este vector es especial, pues carece
de direcci¶on y sentido.
~0 = (0; 0; 0):
Vector unitario de otro dado ~v es aqu¶el que, teniendo la misma direcci¶on y sentido
que el que se da, presenta un m¶odulo igual a 1, se representa como ^v. As¶³
^v =
~v
j~vj
:
4.2.1. Operaciones unarias diferenciales
Para derivar un vector ~v respecto a un par¶ametro t se deriva componente a
componente.
d
dt
~v = (
d
dt
vx;
d
dt
vy;
d
dt
vz):
Para integrar un vector ~v respecto a un par¶ametro t se integra componente a
componente. Z
~v dt = (
Z
vx dt;
Z
vy dt;
Z
vz dt):
4.3. Operaciones vectoriales binarias
Las operaciones binarias necesitan dos vectores para poder operar sobre ellos.
Las m¶as conocidas son:
4.3.1. Equivalencia
Dos vectores son iguales si sus coordenadas son iguales. Es decir
~a =~b ) ax = bx; ay = by; az = bz:
4.3.2. Suma y resta
La suma de varios vectores tambi¶en se denomina resultante de dichos vectores.
Para sumar un vector ~a a otro ~b se suma componente a componente, es decir
~a +~b = (ax + bx; ay + by; az + bz):
Para restar un vector ~a de otro ~b se suma el inverso del vector ~b, es decir:
~a ¡~b = (ax ¡ bx; ay ¡ by; az ¡ bz):
La resta de dos vectores iguales son es el vector cero.
~a ¡~a = ~0:

4.3.3. Producto escalar
El producto escalar de dos vectores da como resultado un escalar, como indica
su nombre. Para multiplicar as¶³ escalarmente un vector ~a por otro ~b se opera
~a ¢~b = j~ajj~bj cos(µ): (4.2)
Siendo µ el ¶angulo que forman los vectores ~a y ~b entre ellos.
El producto escalar de dos vectores, dadas sus componentes, se puede realizar
tambi¶en sabiendo que
~a ¢~b = axbx + ayby + azbz: (4.3)
Observando las relaciones que marcan (4.2) y (4.3) y teniendo presenta adem¶as
la relaci¶on del m¶odulo de un vector expuesta en (4.1) se pueden deducir las siguientes
propiedades del producto escalar:
Es nulo si alguno de los dos vectores es el vector nulo.
Es nulo si los dos vectores son perpendiculares.
Para proyectar un vector ~a sobre un eje marcado por un vector ~b basta con
realizar la operaci¶on
proy~b(~a) =
~a ¢~b
j~bj
:
Dados dos vectores se puede calcular el ¶angulo que forma entre ellos usando
la relaci¶on
cos(µ) =
~a ¢~b
j~ajj~bj
=
q axbx + ayby + azbz
a2
y + a2z
x + a2
q
b2
y + b2z
x + b2
:
4.3.4. Producto vectorial
Introducci¶on
El producto vectorial, representado como ~a £ ~b o bien como ~a ^ ~b, tiene las
siguientes propiedades:
Es perpendicular tanto a ~a como a ~b. Es decir,
³
~a ^~b
´
?~a y
³
~a ^~b
´
?~b.
Su m¶odulo es ab sin ®, siendo ® el ¶angulo que forman entre ellos. Tambi¶en, ¯¯ ¯~a ^~b
¯¯¯
= ab sin ®.
Su sentido est¶a dado por la regla del sacacorchos, entendiendo que hay que
mover el sacacorchos" desde el primer vector al segundo.
C¶alculo de las componentes de ~a ^~b
Demostraremos en 4.3.4, quiz¶as no muy rigurosamente, pero si ganando a cambio
mucho en simplicidad, como se puede llegar a este resultado. En cualquier caso, para
hallar cuales son las componentes del vector producto vectorial basta con saber que
si ~a = ax^{ + ay^| + az^k y ~b = bx^{ + by^| + bz^k, entonces:
~a ^~b =
¯¯¯¯¯¯
^{ ^| ^k
ax ay az
bx by bz
¯¯¯¯¯¯
= (aybz ¡ azby)^{+
(azbx ¡ axbz)^|+
(axby ¡ aybx)^k
(4.4)

Expresi¶on anal¶³tica del producto vectorial
± Tomando ~a ^~b = ~c Ampliacio¶n henos exigido que tanto ~a?~c como que ~b?~c. Es decir
axcx + aycy + azcz = 0
bxcx + bycy + bzcz = 0
: (4.5)
Adem¶as parece l¶ogico suponer que este nuevo vector deber¶a ser indepen-diente"
del sistema de coordenadas que elijamos, con lo cual vamos a tomar
uno en el que el vector ~a coincida con el eje y y el ~b se encuentre contenido en
el plano xy, formando entre ellos un ¶angulo µ.
Despejando cx en una de las ecuaciones (4.5) tenemos que
cx =
¡aycy ¡ azcz
ax
(4.6)
y, sustituyendo en la otra se consigue que
cy =
¡bzczax + bxaycy + bxazcz
byax
: (4.7)
Operando un poco en la expresi¶on (4.7) de tal forma que podamos expresar
cz en funci¶on de cy tendremos que
cz =
cy (byax ¡ bxay)
bxaz ¡ bzax
(4.8)
y ahora no queda m¶as que ver el signi¯cado de esta expresi¶on para lograr el
resultado ¯nal.
De las relaciones (4.5) tenemos que ~c debe ser perpendicular tanto a ~a
como a ~b y, por tanto, en el caso concreto que hemos elegido, ~c debe estar
en el eje z, es decir, ~c = ¸^k. Ahora bien, precisamente por esta misma raz¶on
cy = 0 y, seg¶un la relaci¶on (4.8) cz deber¶³a ser tambi¶en cero, cosa que no tiene
sentido. Una posible soluci¶on ser¶³a hacer ver que la relaci¶on no es v¶alida porque
estamos dividiendo por cero, y, ya que cy tambi¶en es cero, igualar ambos
t¶erminos. As¶³ tendr¶³amos cy = bxaz ¡ bzax y podr¶³amos simpli¯car cy con el
denominador2. Una vez extra¶³do cy se tendr¶³a tambi¶en que cz = byax ¡ bxay,
y s¶olo quedar¶³a hallar cx usando nuevamente las ecuaciones (4.5). Quedar¶³a,
no en s¶³ demostrado, pero si razonado, el por qu¶e de expresar el producto
vectorial de la manera rese~nada en (4.4).
C¶alculo de ¶areas con el producto vectorial
Antes de nada: >c¶omo es posible qu¶e el producto vectorial, que da como resultado
un vector, sea reutilizable para calcular un ¶area?. Responder a esta pregunta es
sencillo si, para ello, tenemos en cuenta el m¶odulo del producto vectorial, que ser¶a un
escalar.
Sabemos ya que j~a ^ ~bj = ab sin Á donde Á representa el ¶angulo formado por
ambos vectores. Esto puede verse en la ¯gura 4.1. Tambi¶en nos damos cuenta que
b sin Á puede interpretarse como la altura" del tri¶angulo formado por ~a, ~b y la
uni¶on de sus dos extremos. Con lo que resulta que j~a ^~bj resulta ser la base a por
la altura b sin Á, y por tanto
j~a ^~bj
2
= Atria
donde Atria es el ¶area del tri¶angulo anteriormente dicho.
2Teniendo presente que esta simpli¯caci¶on est¶a muy tomada por los pelos... ya que se trata de
0
0 .

a
b
b sin
b cos
f
f
f
Figura 4.1: El ¶angulo entre dos vectores y sus proyecciones.
4.3.5. Producto mixto
A veces se de¯ne el producto mixto entre tres vectores ~a, ~b y ~c como
~a ¢ (~b ^ ~c): (4.9)
Este producto, cuyo resultado puede verse que va a ser un escalar, se puede calcular
tambi¶en como el determinante de la matriz 3 ¤ 3 que se forma con las componentes
de los vectores, es decir
¯¯¯¯¯¯
ax ay az
bx by bz
cx cy cz
¯¯¯¯¯¯
= axbxcx + cxaybz + azbxcy ¡ azbycx ¡ aybxcz ¡ axbzcy:
Una de las utilidades del producto mixto es que da el volumen de un parale-lep
¶³pedo formado con las aristas de los vectores ~a, ~b y ~c, ya que si manejamos un
poco (4.9) tenemos que:
~a ¢ (~b ^ ~c) =
= aj~b ^ ~cj cos Á
= abc sin Ã cos Á:
donde bc sin Ã no es sino el ¶area de la base del paralelogramo (ver secci¶on 4.3.4) y
a cos Á resulta ser la altura de dicho paralelep¶³pedo. El ¶area de la base por la altura
nos da el volumen de este tipo de cuerpos geom¶etricos.
± Ser¶³a un buen ejercicio para el lector intentar demostrar m¶as rigurosa- Ampliaci¶on
mente estas ¶ultimas a¯rmaciones

Cap¶³tulo 5
Cinem¶atica
5.1. Introducci¶on
Cinem¶atica es la parte de la f¶³sica que estudia el movimiento de los cuerpos,
aunque sin interesarse por las causas que originan dicho movimiento. Un estudio de
las causas que lo originan es lo que se conoce como din¶amica.
Las magnitudes que de¯ne la cinem¶atica son principalmente tres, la posici¶on, la
velocidad y la aceleraci¶on.
Posici¶on es el lugar en que se encuentra el m¶ovil en un cierto instante de tiempo t.
Suele representarse con el vector de posici¶on ~r. Dada la dependencia de este
vector con el tiempo, es decir, si nos dan ~r(t), tenemos toda la informaci¶on
necesaria para los c¶alculos cinem¶aticos.
Velocidad es la variaci¶on de la posici¶on con el tiempo. Nos indica si el m¶ovil se
mueve, es decir, si var¶³a su posici¶on a medida que var¶³a el tiempo. La velocidad
en f¶³sica se corresponde al concepto intuitivo y cotidiano de velocidad.
Aceleraci¶on indica cu¶anto var¶³a la velocidad al ir pasando el tiempo. El concepto
de aceleraci¶on no es tan claro como el de velocidad, ya que la intervenci¶on
de un criterio de signos puede hacer que interpretemos err¶oneamente cu¶ando
un cuerpo se acelera (a > 0) o cu¶ando se decelera" (a < 0). Por ejemplo,
cuando lanzamos una piedra al aire y ¶esta cae es f¶acil ver que, seg¶un sube
la piedra, su aceleraci¶on es negativa, pero no es tan sencillo constatar que
cuando cae su aceleraci¶on sigue siendo negativa porque realmente su veloci-dad
est¶a disminuyendo, ya que hemos de considerar tambi¶en el signo de esta
velocidad.
5.2. Velocidad
Se de¯ne velocidad media como
v~m =
¢~r
¢t
tomando los incrementos entre los instantes inicial y ¯nal que se precisen.
No obstante, aunque la velocidad media es una magnitud ¶util, hay que destacar
que en su c¶alculo se deja mucha informaci¶on sin precisar. As¶³, aunque sepamos que
la velocidad media de un m¶ovil desde un instante 1 a otro 2 ha sido tantos" metros
por segundo, no sabremos si los ha hecho de forma constante, o si ha ido muy lento
al principio y r¶apido al ¯nal o si. . . por eso se de¯ne una magnitud que exprese
23

CAP¶ITULO 5. CINEM¶ATICA
la velocidad instant¶anea, es decir, la velocidad en cierto y determinado instante
y que pueda calcularse como una velocidad media donde los intervalos sean tan
peque~nos que pueda decirse exactamente a qu¶e velocidad se desplazaba el m¶ovil en
cada instante. Es f¶acil darse cuenta de que esta de¯nici¶on se logra tomando como
velocidad instant¶anea:
~v = l¶³m
¢t!0
¢~r
¢t
y por tanto, coincide con la de¯nici¶on de derivada respecto al tiempo. As¶³ pues se
de¯ne ¯nalmente
~v =
d
dt
~r:
De esta de¯nici¶on se obtienen algunas consecuencias:
La direcci¶on de ~v va a ser siempre tangente a la trayectoria.
El m¶odulo de ~v puede calcularse, adem¶as de operando sobre el vector ~v, sa-biendo
que
j~vj =
d
dt
s(t)
siendo s(t) la distancia que el m¶ovil ha recorrido sobre la trayectoria1.
5.3. Aceleraci¶on
Aceleraci¶on es la variaci¶on de la velocidad en la unidad de tiempo. Se puede
de¯nir una aceleraci¶on media entre dos instantes, inicial y ¯nal, como
~am =
~vf ¡~vi
tf ¡ ti
y, de manera an¶aloga a la velocidad, puede de¯nirse una aceleraci¶on instant¶anea
llevando estos instantes inicial y ¯nal muy cerca uno del otro, hasta tener as¶³ que
la aceleraci¶on instant¶anea es la derivada de la velocidad respecto al tiempo
~a =
d
dt
~v(t):
5.4. Componentes intr¶³nsecas de la aceleraci¶on
Tomando el vector velocidad como un m¶odulo por un vector unitarios, es decir,
como
~v = j~vj^v
y derivando se tiene que, utilizando la regla del producto para las derivadas (ap¶endi-ce
C),
d
dt j~vj)^v
| {z }
tangencial
~a = (
+j~vj
d
dt
^v
| {z }
normal
:
De estas dos componentes la primera se denomina aceleraci¶on tangencial porque,
como se desprende de su propia de¯nici¶on, su direcci¶on es la del vector unitario ^v y
es por tanto, tangente a la trayectoria. La otra componente es la aceleraci¶on normal.
1Intuitivamente, para un autom¶ovil ~r ser¶³an las coordenadas del coche vistas desde un sistema
de referencia elegido, y s(t) ser¶³a la distancia recorrida por el autom¶ovil que va marcando el
cuentakil¶ometros.

De la aceleraci¶on tangencial diremos que su m¶odulo es
j~atj =
d
dt j~vj (5.1)
y su direcci¶on
^v =
~v
j~vj
:
Esta ~at se encarga de medir" la variaci¶on de la velocidad sin importarle su direcci¶on
ni sentido, sino solo su m¶odulo, es decir, su intensidad".
En cuanto a la aceleraci¶on normal, se puede demostrar que su m¶odulo es
j~anj = j~vj2
R
; (5.2)
siendo R el radio de curvatura de la trayectoria, y que su direcci¶on es siempre
perpendicular a la trayectoria y hacia el interior de la curva".
5.5. Clasi¯caci¶on de movimientos
Los movimientos se pueden clasi¯car seg¶un las componentes intr¶³nsecas de su
aceleraci¶on.
1. at = 0
a) an = 0. Movimiento rectil¶³neo a velocidad constante.
b) an = cte. Movimiento circular uniforme.
c) an6= cte. Movimiento circular acelerado.
2. an = 0
a) at = 0. Movimiento rectil¶³neo a velocidad constante.
b) at = cte. Movimiento rectil¶³neo uniformemente acelerado.
c) at6= cte. Movimiento rectil¶³neo acelerado.
3. an6= 0 y at6= 0. Movimiento curvil¶³neo.
5.6. Composici¶on de movimientos
Los problemas de composici¶on de movimientos tienen la di¯cultad de saber res-pecto
a que sistema estamos resolviendo y por tanto determinar siempre las magni-tudes
respecto al sistema apropiado, bien el especi¯cado por el problema, bien uno
elegido adecuadamente. Es com¶un en este tipo de problemas la presencia de m¶as de
un m¶ovil y hay que ser muy cuidadoso para identi¯car correctamente que m¶oviles
se mueven y respecto a qu¶e.
5.6.1. Translaci¶on pura
Sus relaciones, que pueden deducirse f¶acilmente de la suma vectorial y posterior
derivaci¶on respecto al tiempo, son:
~r = ~r0 +~r0
~v = ~v0 +~v0
~a = ~a0 +~a0
(5.3)

Piedra
que cae.
Coche que
avanza
r
r
r
c
p
cp
Figura 5.1: Relaci¶on vectorial entre unos y otros sistemas. El conductor ver¶a la
piedra que cae como ~rcp = ~rc ¡~rp.
En donde intervienen el sistema quieto" y el que se mueve", que es el pri-mado".
Las magnitudes con el sub¶³ndice 0 son las relativas entre los sistemas de
referencia.
Una estrategia que suele resultar bastante inteligible de plantear es la siguiente:
1. Plantear un sistema ¯jo, respecto al cual conocemos, al menos, c¶omo es el
movimiento de uno de los otros sistemas.
2. Dibujar entonces el vector de posici¶on que buscamos (generalmente el de un
sistema respecto al otro).
3. Relacionar estos vectores entre s¶³ como sumas unos de los otros.
Se ha dibujado esto en la ¯gura 5.1.
Una vez que conocemos el vector de posici¶on se puede extraer el resto de infor-maci
¶on derivando o realizando la operaci¶on matem¶atica necesaria.
5.6.2. Rotaci¶on pura
En este caso suponemos que un sistema gira respecto al otro con una velocidad
angular constante !, pero manteniendo el origen en com¶un.
La f¶ormula interesante es la que relaciona sus velocidades
~v = ~v0 + ~! £~r (5.4)
que presenta una di¯cultad un poco mayor de deducci¶on, y por eso no se expresa
aqu¶³.
Las magnitudes que aparecen en esta f¶ormula son ~v, que es la velocidad que el
m¶ovil presenta respeto al sistema ¯jo". ~v0, la velocidad del m¶ovil vista desde el
sistema que rota, y ! que es la velocidad angular con la cual el sistema m¶ovil rota
respecto al ¯jo", aunque siempre manteniendo en com¶un su origen de coordenadas.
Por ejemplo, si hubiera una mosca posada en el eje de un tocadiscos y girando
con ¶el a una cierta velocidad angular !, que observara a un mosquito avanzar
por el disco con una velocidad ~v0, vista desde el punto de vista de la mosca, que
est¶a rotando, en este caso:
~v Ser¶³a la velocidad del mosquito vista desde el eje del tocadiscos, pero el
observador ¯jo, es decir, sin girar.
~v0 es la velocidad con la cual la mosca, que gira, ve al mosquito desplazarse
por el disco.

! es la velocidad angular del disco.
~r es el vector de posici¶on del mosquito, en el sistema ¯jo.
5.7. Resoluci¶on de problemas
5.7.1. Tiro parab¶olico
Se denomina tiro parab¶olico, en general, a aquellos movimientos que suceden de
forma bidimensional sobre la super¯cie de la tierra.
Para este tipo de m¶oviles el movimiento se descompone en sus componentes2 x
e y. El movimiento en x no sufre aceleraci¶on, y por tanto sus ecuaciones ser¶an
Eje x
½
x = x0 + v0xt
vx = v0x
(5.5)
pero en cambio en el eje y se deja sentir la fuerza de la gravedad, supuesta constante3
y por tanto sus ecuaciones ser¶an
Eje y
½
y = y0 + v0yt ¡ 1
2 gt2
vy = v0y ¡ gt
: (5.6)
Algunas preguntas t¶³picas del tiro parab¶olico son calcular el alcance y altura
m¶axima. Estas preguntas se pueden contestar sabiendo que la altura m¶axima se
alcanzar¶a cuando vy = 0. De esta condici¶on se extrae el tiempo que tarda en alcanzar
la altura m¶axima y sustituyendo en la ecuaci¶on de las y se obtiene la altura m¶axima.
El alcance m¶aximo se puede calcular razonando que, para cuando esto suceda, el
m¶ovil volver¶a estar al nivel del suelo y por tanto y = 0, sustituyendo se obtiene t
y, sustituyendo ¶este en las x el resultado. Otras cantidades se pueden conseguir de
manera similar.
¦ x0 e y0 ser¶an las coordenadas donde el m¶ovil se encuentra en el instante Nota
t = 0, inicio del movimiento, y vx0 y vy0 la velocidad con la que se mueve
en ese instante. Si nos han indicado que el m¶ovil se mov¶³a con una velocidad
v formando un ¶angulo ® con la horizontal se puede ver muy f¶acilmente que,
entonces, vx0 = v cos ® y vy0 = v sin ®.
A su vez el signi¯cado de las variables x e y es el siguiente: ¶estas nos
indican a que distancia horizontal (x) y altura (y) se encuentra el m¶ovil en cada
instante de tiempo t, considerando que estamos tomando como origen para
medir estas distancias horizontales y alturas desde el sistema de coordenadas
respecto al cual estemos tomando todos los dem¶as datos.
± Se podr¶³a hacer un estudio m¶as complejo incluyendo el rozamiento del Ampliaci¶on
aire. Para esto habr¶a que modi¯car las ecuaciones x e y a las nuevas ecuaciones
deducidas en el ap¶endice B.
5.7.2. Componentes intr¶³nsecas
P Sea un m¶ovil cuyo vector de posici¶on es Problema
~r = (7 ¡ 3t)^{ + (5t ¡ 5t2)^| + 8^k (m):
Calcular su velocidad, aceleraci¶on y componentes intr¶³nsecas de ¶esta,
as¶³ como el radio de la trayectoria para t = 0;5s.

R Derivo para encontrar ~v y ~a. Una primera vez Resoluci¶on
~v =
d
dt
~r = ¡3^{ + (5 ¡ 10t)^|
m
s
y una segunda vez
~a =
d
dt
~v = ¡10^|
m
s2 :
Ahora calculo el m¶odulo de la velocidad:
j~vj =
p
9 + (5 ¡ 10t)2 =
p
m
34 ¡ 100t + 100t2s
que, derivado respecto al tiempo nos dar¶a el m¶odulo de ~at.
j~atj =
d
dt
p
34 ¡ 100t + 100t2 =
100t ¡ 50
p34 ¡ 100t + 100t2
m
s2
y multiplicando por el unitario de ~v, que es
^v = ¡3^{ + (5 ¡ 10t)^|
p34 ¡ 100t + 100t2
nos da el vector ~at
~at =
100t ¡ 50
34 ¡ 100t + 100t2 (¡3^{ + (5 ¡ 10t)^|):
m
s2
Por ultimo ¶podemos calcular ~an como ~a ¡ ~at. Haciendo las oportunas
sustituciones tendremos que para t = 0;5s, ~v = ¡3^{m
, ~a = ¡10^|m
s s2 ,
~at = ~0m
s2 con lo cual ~an = ¡3^|m
s2 y de esta forma, podremos despejar el
radio de la trayectoria, que ser¶a
R =
v2
an
= 3m:
5.7.3. C¶alculo de trayectorias
Problema P Dado el vector de posicio¶n de un mo¶vil
~r = 15t^{ + (200 ¡ 5t2)^|;
calcule la ecuaci¶on de su trayectoria.
Resolucio¶n R Este tipo de problemas se resuelve en general despejando t en una
de las ecuaciones de x o de y y sustituyendo en la otra, encontrando
as¶³ x en funci¶on de y o al rev¶es. En este caso tenemos que
x = 15t ) t =
x
15
y sustituyendo en
y = 200 ¡ 5t2
tendremos
y = 200 ¡ 5
³ x
15
´2
) y = 200 ¡
1
45
x2:
2Vectores ^{ y ^|.
3Aproximaci¶on v¶alida siempre que el tiro discurra en la super¯cie terrestre o apreciablemente"
en la super¯cie terrestre.

Cap¶³tulo 6
Din¶amica
6.1. Introducci¶on
As¶³ como la cinem¶atica se encarga de la descripci¶on del movimiento de los cuer-pos,
aunque sin entrar en detalles de la causa que hace mover a ¶estos, la din¶amica
estudia precisamente por qu¶e se mueven los cuerpos, es decir, cu¶ales son las causas
que crean la variaci¶on de su estado de movimiento.
6.2. Leyes de Newton
6.2.1. Ley de la inercia
La ley de la inercia se podr¶³a enunciar como
. Todo cuerpo permanece en su estado actual de movimiento con Recuerda
velocidad uniforme o de reposo a menos que sobre ¶el act¶ue una fuerza
externa neta o no equilibrada.
donde la fuerza neta de la que hablamos antes ser¶³a la suma vectorial de todas las
fuerzas que puedan actuar separadamente sobre el cuerpo.
¦ ¶Esta es la raz¶on por la cual es tan peligroso para los astronautas en Nota
el espacio separarse de la nave sin un cord¶on que los una a ella, ya que si
chocan con algo y salen impulsados, como no act¶ua ninguna fuerza sobre
ellos, seguir¶an desplaz¶andose uniformemente y separ¶andose de la nave sin
posibilidad de volver a ella (a no ser que tengan un peque~no impulsor).
6.2.2. Segunda ley de Newton
Esta ley es la m¶as importante en cuanto nos permite establecer una relaci¶on
num¶erica entre las magnitudes fuerza" y aceleraci¶on". Se podr¶³a enunciar como
. La aceleraci¶on que toma un cuerpo es proporcional a la fuerza neta Recuerda
externa que se le aplica.
La constante de proporcionalidad es la masa del cuerpo, con lo que num¶ericamente
esta expresi¶on se denota como
~F = m~a (6.1)
o, en componentes
Fi = mai; i = 1; 2; 3 (6.2)
29

CAP¶ITULO 6. DIN¶AMICA
donde ~F representa la resultante de todas las fuerzas externas al cuerpo, es decir,
la suma de dichas fuerzas. ~F =
P ~Fj ; j = 1; :::
Esta expresi¶on nos relaciona ~F, m y ~a de una forma un¶³voca. B¶asicamente nos
dice que el resultado que producen una serie de fuerzas sobre un cuerpo es que dicho
cuerpo se acelere en la misma direcci¶on y sentido que la suma de las fuerzas que le
son aplicadas y con una intensidad o m¶odulo que ser¶a la misma que la resultante
de las fuerzas dividida entre la masa del cuerpo.
Nota ¦ As¶³ pues un cuerpo experimenta una aceleracio¶n mientras esta¶ siendo
sometido a una fuerza resultante no nula. Si dicha fuerza cesa el cuerpo ad-quirir
¶³a un movimiento rectil¶³neo uniforme o se quedar¶³a quieto, seg¶un el caso.
6.2.3. Tercera ley de Newton
La tercera ley de Newton expresa una interesante propiedad de las fuerzas: ¶estas
siempre se van a presentar en parejas. Se puede enunciar como
Recuerda . Si un cuerpo A ejerce, por la causa que sea, una fuerza F sobre
otro B, este otro cuerpo B ejercer¶a sobre A una fuerza igual en m¶odulo
y direcci¶on, pero de sentido contrario.
Gracias a esta ley1 se pueden entender fen¶omenos como que, para saltar hacia
arriba <empujamos la Tierra con todas nuestras fuerzas hacia abajo!. Al hacer esto
la Tierra tambi¶en ejerce esta misma fuerza con nosotros, pero con sentido contrario
(es decir, hacia arriba) y como la masa de la Tierra es enorme en comparaci¶on
con la nuestra, el resultado es que nosotros salimos despedidos hacia arriba pero
la Tierra no se mueve apreciablemente. As¶³ tambi¶en si empujamos una super¯cie
puntiaguda con mucha fuerza, podemos clav¶arnosla, porque dicha super¯cie tambi¶en
estar¶a empujando nuestro dedo con la misma fuerza que nosotros a ella, y como la
super¯cie de la aguja es much¶³simo menor la presi¶on que esta hace sobre nuestro
dedo es muy grande.
Nota ¦ Entonces, si a toda fuerza que se ejerce se opone otra de sentido contrario
>no deber¶³an anularse las fuerzas y nada se podr¶³a mover?. No, porque las
fuerzas se ejercen en cuerpos diferentes. As¶³ en el ejemplo del salto, nosotros
empujamos a la Tierra y la Tierra a nosotros, pero estas fuerzas no se anulan
porque, como es evidente, nosotros y la Tierra somos cuerpos distintos.
6.3. Fuerzas especiales que aparecen en problemas
6.3.1. Normal
Por normal se entiende la fuerza con la que una super¯cie se opone a un cuerpo
que se le sit¶ua encima. Si no existiera esta fuerza el cuerpo se hundir¶³a" en la
super¯cie. ¶Esta es, por tanto, la fuerza de reacci¶on que, obediente al tercer principio
de Newton, la super¯cie opone al empuje que el cuerpo, por encontrarse encima,
hace sobre ella.
Esta fuerza es siempre normal a la super¯cie, es decir, perpendicular a ¶esta. Para
calcular su valor hay que ser bastante cuidadoso y hacer un balance de las fuerzas
en los ejes que tomemos, utilizando la normal para compensar las otras fuerzas de
la forma en que sea necesario.
Problema P Calcule la normal que una mesa ejerce sobre un cuerpo de 10kg si
el cuerpo est¶a en reposo.
1Tambi¶en llamada ley de acci¶on y reacci¶on

R Si el cuerpo est¶a en reposo signi¯ca que su aceleraci¶on total es Resoluci¶on
nula. Entonces aplicando la segunda ley de Newton a un eje vertical
tendremos que
0 = N ¡ P
donde hemos supuesto que la mesa est¶a perfectamente horizontal y por
tanto la normal tendr¶a s¶olo una componente en el eje y. As¶³ tendremos
que N = P y por tanto en este caso N = mg.
El c¶alculo de la normal en un caso donde haya un cuerpo desliz¶andose por una
rampa puede encontrarse en la secci¶on 6.6.
6.3.2. Rozamiento
Entre dos super¯cies
El rozamiento entre super¯cies se expresa como
Fr = ¹N;
siendo siempre de sentido opuesto al del movimiento. Este resultado no se puede
demostrar" porque se trata de un resultado emp¶³rico, es decir, fruto de la experi-mentaci
¶on.
El coe¯ciente de rozamiento ¹ es adimensional y expresa as¶³ la relaci¶on entre
la normal que el cuerpo ejerce, es decir, la fuerza con la que el cuerpo empuja la
super¯cie debajo de la cual se encuentra, y el rozamiento que va a sufrir por causa
de este empuje. Puede haber dos tipos de coe¯ciente de rozamiento. Un ¹ est¶atico,
que se aplica cuando el cuerpo est¶a quieto y que as¶³, utilizado en Fr = ¹N nos va a
ofrecer la fuerza m¶axima con la que el rozamiento se va a resistir a que se mueva un
cuerpo que est¶a quieto, y un ¹ din¶amico que, aplicado en la f¶ormula de rozamiento,
nos dice la fuerza que el rozamiento est¶a realizando contra un movimiento.
P Un cuerpo de 4kg est¶a deslizando por una super¯cie lisa con coe¯- Problema
ciente de rozamiento (din¶amico) ¹ = 0;25. Si sobre este cuerpo no act¶uan
m¶as fuerzas que el peso y dicha fuerza de rozamiento >con qu¶e acelera-ci
¶on se mueve el cuerpo?.
R Aplicando la ecuaci¶on de Newton al eje y del movimiento obtene- Resoluci¶on
mos que, en este eje, las fuerzas que aparecen son el peso y la normal y,
por tanto,
N ¡ P = may:
Como ay = 0 (un cuerpo sobre una super¯cie no va botando" sobre
ella, su altura, medida sobre la super¯cie, es siempre 0.) tendremos que
N = mg. Aplicando ahora Fx = max tenemos que la ¶unica fuerza en el
eje x es la de rozamiento, y por tanto
Fx = ¡Fr = ¡¹N = max ) ax = ¡¹g
de donde ax = ¡2;45m
s2 . El signo `-' se debe a que, como estamos su-poniendo
impl¶³citamente que el cuerpo avanza hacia el signo positivo
de las x, el rozamiento se opondr¶a al avance y tendr¶a, por tanto, signo
negativo.

Con un °uido
± Rozamiento con un °uido2 se expresa con Ampliaci¶on
~Fr = ¡K~v
o bien
Fr = ¡Kv2
u otras potencias de v. Una aplicaci¶on algo compleja sobre la forma de utilizar
esta fuerza de rozamiento puede verse en el ap¶endice B. No es sencillo demos-trar
por qu¶e esta contribuci¶on nos aporta el rozamiento contra un °uido y,
en algunos casos, es por medio de la experimentaci¶on como se encuentra una
f¶ormula emp¶³rica m¶as precisa.
Tensi¶on
En problemas que intervienen cuerdas o poleas tensi¶on es la fuerza que liga unos
cuerpos y otros a trav¶es de la cuerda. La tensi¶on en cada extremo de una misma
cuerda es siempre igual pero de sentido contrario. Si esta tensi¶on supera un cierto
valor cr¶³tico la cuerda se romper¶³a.
6.4. El momento lineal
La ley de Newton, expresada como ~F = m~a puede ser utilizada tambi¶en para
demostrar otras relaciones interesantes, siempre que se manipule adecuadamente.
Por ejemplo, si de¯nimos una cantidad ~p a la que llamaremos cantidad de mo-vimiento,
podemos decir que una fuerza es la encargada de variar la cantidad de
movimiento sobre un cuerpo. De esta forma de¯namos ~p tal que
~F =
d
dt
~p:
La pregunta ser¶a ahora >tendr¶a ~p alguna expresi¶on conocida?. Supongamos que un
cuerpo con masa constante va a cierta velocidad ~v. Una fuerza sobre ¶el deber¶a produ-cirle
una aceleraci¶on y, por tanto variar su velocidad y su momento lineal. As¶³ pues
velocidad y momento lineal deben de ir relacionados de alguna forma. Efectiva-mente
tomando ~p = m~v nos damos cuenta de que d
dtm~v cuando m es constate es
m d
~v = m~a = F ~.
dtPor tanto hemos descubierto una nueva magnitud p ~que nos sera ¶de gran utilidad
para desarrollos sucesivos.
Nota ¦ Una forma intuitiva de comprender el momento lineal es como una forma
de medir la di¯cultad de llevar una part¶³cula hasta el reposo. As¶³ es claro
que, cuanto m¶as masivo sea un cuerpo y m¶as velocidad tenga, tanto m¶as nos
costar¶a parar" el movimiento de dicho cuerpo.
6.4.1. Conservaci¶on del momento lineal
Cuando la resultante de las fuerzas externas sobre un sistema es nula, >qu¶e su-cede
con ~p?. Como la fuerza es la derivada del momento lineal respecto al tiempo,
obtenemos que, cuando la fuerza total es cero, esta cantidad que se deriva debe ser
constante y, por tanto, si ~F = ~0 esto supone ~p = cte. Hemos obtenido as¶³ que esta
magnitud tan interesante, el momento lineal, se conserva, es decir, no var¶³a, cuando
no aparecen fuerzas externas sobre un objeto. Por tanto podemos decir que
~pi = ~pf :
2Aire, agua, aceite...

mg sen a
x
y
mg cos a
a
N
mg
a
Figura 6.1: Descomposici¶on de las fuerzas en un plano inclinado.
La importancia de esta igualdad se podr¶a ver mejor cuando hablemos de los
sistemas de part¶³culas, concretamente en la secci¶on 8.3.3.
6.5. Conservaci¶on de la energ¶³a
Cuando en un problema intervienen sobre el sistema ¶unicamente fuerzas con-servativas3
se pude aplicar el teorema de conservaci¶on de la energ¶³a. Esto supone
que
Ei = Ef ;
siendo Ei y Ef las sumas de las energ¶³as potenciales m¶as la energ¶³a cin¶etica en los
momentos i y f4.
La explicaci¶on de esta igualdad tan interesante no se expresa aqu¶³ porque se
ver¶a m¶as concretamente en el cap¶³tulo 7.4.
6.6. Resoluci¶on de problemas
6.6.1. Planos inclinados
Es com¶un en los problemas la presencia de planos inclinados. En estos casos
habr¶a que tener en cuenta que, as¶³ como la gravedad siempre se presenta vertical, la
normal ser¶a perpendicular al plano inclinado, por lo que ning¶un sistema de coorde-nadas
ortogonal tendr¶a exactamente comprendidas las fuerzas en acci¶on en sus ejes.
Esta peque~na di¯cultad se soslaya de una manera simple, se proyectan las fuerzas
sobre los ejes que estemos utilizando.
Una buena elecci¶on suele ser tomar el eje y en la normal al plano inclinado, y el
eje x acorde con su super¯cie de deslizamiento. De esta forma la normal estar¶a to-talmente
comprendida en el eje y, y s¶olo habr¶a que considerar las proyecciones de
g usuales; g cos ® para la normal y g sin ® la componente de la gravedad que hace
desplazarse el veh¶³culo hacia abajo en el plano inclinado. Todo esto se puede ver en
la ¯gura 6.1.
P Un cuerpo desliza por una rampa inclinada 30o y con un coe¯ciente Problema
3B¶asicamente, siempre que no hay rozamiento.
4Llamados as¶³ por inicial y final.

m m
1 2
m
1
a b
2
m
Figura 6.2: >Cu¶al ser¶a la aceleraci¶on de este sistema?
de rozamiento ¹ = 0;2. Calcular la aceleraci¶on con la que desciende
suponiendo que g = 9;8m
s2 .
Resolucio¶n R Tomemos para enfocar este problema el gra¶¯co representado en la
¯gura 6.1. Habremos de aplicar la ecuaci¶on de Newton
~F = m~a
para un sistema adecuado de ejes. Se van a tomar como ejes unos tales
que el eje x presente la misma inclinaci¶on que la rampa. De esta forma
planteando la ecuaci¶on primero para el eje y:
Fy = may
y como las fuerzas en el eje y son la normal (componente positiva) y la
proyecci¶on sobre este eje y del peso (componente negativa) tendremos
que
N ¡ mg cos 30 = ma:
Ahora hay que darse cuenta que, en el eje y el cuerpo no se acelera
porque, como en ning¶un momento se despega de la super¯cie, siempre
su y = y, por tanto, ay = 0. As¶³ que tenemos que N ¡ mg cos 30 = 0 ) N = mg cos 30.
Para el eje x tenemos dos fuerzas, la proyecci¶on sobre nuestro eje x
del peso y la fuerza de rozamiento. As¶³ pues
Fx = max ) mg sin 30 ¡ ¹N = max
y haciendo las oportunas sustituciones podemos despejar ax, que es la
aceleraci¶on del sistema.
ax = g sin 30 ¡ ¹g cos 30 ¼ 3;2
m
s2 :
Cuando aparecen varios cuerpos unidos por cuerdas hay que hacer este mismo
an¶alisis para cada cuerpo, incorporando como fuerza la tensi¶on que ejercen las cuer-das
y d¶andose cuenta de que ax ser¶a la misma para todos los cuerpos, puesto que
si se encuentran unidos por cuerdas su movimiento ser¶a solidario.
Problema P Encontrar la aceleracio¶n del sistema dibujado en la ¯gura 6.2.

R Tomemos primero el cuerpo 1 y analicemos las fuerzas que apare-
Resoluci¶on
cen sobre ¶el. Podemos, aprovechando el an¶alisis del problema anterior,
darnos cuenta de que un estudio de las fuerzas perpendiculares a la su-per
¯cie va a darnos s¶olo como resultado que N1 = m1g cos ®. As¶³ que
las fuerzas horizontales ser¶an, tomando como sentido positivo hacia la
derecha:
1. La tensi¶on, positiva.
2. La componente x del peso, de valor ¡m1g sin ®.
3. El rozamiento, que ser¶a ¡¹1N1 = ¡¹1m1g cos ®.
Para el cuerpo 2 se tendr¶an las fuerzas:
1. Tensi¶on, negativa para este cuerpo. ¡T
2. Componente x del peso: m2g sin ¯.
3. Rozamiento, ¡¹2N2 = ¡¹2m2g cos ¯.
Queda ahora plantear el sistema de ecuaciones que resolver¶a este proble-ma.
Antes hay que darse cuenta que la componente x de la aceleraci¶on
debe ser la misma para ambos cuerpos, ya que van solidarios gracias a
la cuerda. Llamaremos a esta componente de la aceleraci¶on simplemente
a.
T ¡ m1g sin ® ¡ ¹1m1g cos ® = m1a
¡T + m2g sin ¯ ¡ ¹2m2g cos ¯ = m2a
¾
:
Resolviendo este sistema (por ejemplo sumando las ecuaciones miembro
a miembro) se obtiene f¶acilmente que
a =
m2 sin ¯ ¡ ¹2m2 cos ¯ ¡ m1 sin ® ¡ ¹1m1 cos ®
m1 + m2
g:
6.6.2. Curvas
Cuando aparecen problemas de estabilidad en las curvas pueden ser de los tipos
explicados a continuaci¶on y cuya representaci¶on se ha pretendido en la ¯gura 6.3.
Curvas sin peraltar
En estos casos la fuerza de rozamiento es la que nos proporciona toda la com-ponente
normal que servir¶a para tomar la curva. Siempre que tengamos que ¶esta
es mayor que la aceleraci¶on normal el autom¶ovil ser¶a capaz de tomar la curva, es
decir, el caso l¶³mite se alcanza cuando
Fr = man = m
v2
R
.
Curvas peraltadas sin rozamiento
En estos casos se toma la proyecci¶on de la normal sobre la horizontal como
causante de la fuerza centr¶³peta. Este caso se puede ver en la ¯gura 6.3b y se tiene,
simplemente, que:
tan ® =
mv2
R
mg
=
v2
Rg
:

mg
a)
F r
mg
b)
FI - 1313 - J
mg
F n
Ángulo
máximo
c)
N
a
Figura 6.3: Distintas situaciones ante una curva.
Curvas peraltadas con rozamiento
Este es un caso bastante m¶as complejo de analizar. Podr¶³a ser un buen ejercicio
para el lector intentar demostrar que, en este caso, la velocidad l¶³mite para tomar
la curva siendo g la aceleraci¶on de la gravedad, ¹ el coe¯ciente de rozamiento, ® el
¶angulo de inclinaci¶on de la curva y R el radio de la misma, es
v =
r
Rg
¹ + tan ®
1 ¡ ¹ tan ®
:
Vuelcos
En otras situaciones se pide que analicemos si vuelca o no un autom¶ovil. Se
considera que vuelca cuando la fuerza sobre el centro de masas supera el ¶angulo que
forma el centro de masas con alguno de los extremos donde se apoya el veh¶³culo.
Un dibujo puede verse en la ¯gura 6.3. (Este apartado necesita actualizaci¶on).
6.6.3. Casos l¶³mite
Es com¶un la existencia de problemas en los que se nos pregunta por un caso
l¶³mite, relacionado con cuando un m¶ovil se saldr¶a de un determinado recorrido,
o podr¶a dar una vuelta completa en un bucle, o similar. En estos casos hay que
tener en cuenta, simplemente, que un cuerpo permanecer¶a adherido a una super¯cie
mientras exista una cierta reacci¶on de la super¯cie al cuerpo, es decir, mientras la
normal no sea nula. Cuando la normal es nula estamos ante el caso l¶³mite.
Tambi¶en es muy conveniente recordar que, en la mayor¶³a de estos casos, los
cuerpos siguen una trayectoria circular. Pues bien, habr¶a que recordar que este
recorrido circular s¶olo es posible si existe una aceleraci¶on centr¶³peta del m¶odulo
adecuado a la velocidad y radio de la trayectoria, (ver (5.1) y (5.2)) con lo que
habr¶a que realizar la descomposici¶on oportuna de fuerzas para ver qu¶e parte es la
que suministra esta componente y, cuando las fuerzas exteriores no sean capaces de
suministrar esta aceleraci¶on normal, nos hallaremos con el caso l¶³mite y el cuerpo
se saldr¶³a de su trayectoria circular o, en de¯nitiva, dejar¶³a de hacerla.
Problema P Calcular la altura m¶³nima desde la que hay que dejar caer un
objeto para que logre dar la vuelta a un bucle entero, como el dibujado
en la ¯gura 6.4. Se desprecian todos los rozamientos que pudiere haber.

h
R
A
B
Figura 6.4: >Desde qu¶e altura podr¶a una masa realizar un bucle?.
Resolucio¶n R Analizando las fuerzas que se ejercen sobre el cuerpo cuando ¶este
se encuentre en el punto B de la trayectoria, tenemos que, tomando
como sentido positivo hacia arriba, el peso ser¶a ¡mg, la normal en
este caso es hacia abajo porque la fuerza que realiza la super¯cie sobre
el cuerpo es siempre evitando que este atraviese" la super¯cie, y en
este caso atravesar" la super¯cie supondr¶³a empujarla en exceso hacia
arriba, con lo cual, tomando N como el m¶odulo de la normal, la normal
ser¶a ¡N. Por ¶ultimo el efecto de estas dos fuerzas ser¶a producir una
aceleraci¶on pero, como en este caso el objeto est¶a rotando, no ser¶a una
aceleraci¶on cualquiera sino una aceleraci¶on puramente normal y, por
tanto, de m¶odulo
a =
v2
R
y sentido tambi¶en hacia abajo (hacia el centro de la curva). De esta
manera tendremos que el an¶alisis de fuerzas en la parte m¶as alta del
bucle (punto B) es
¡mg ¡ N = ¡m
v2
R
:
>Qu¶e signi¯ca esta f¶ormula?. Lo que signi¯ca es que son el peso y la
normal, los que empujan" al cuerpo hacia abajo oblig¶andole a girar y
realizar una trayectoria circular. Ahora bien, si mentalmente" vamos
disminuyendo v en la f¶ormula, nos damos cuenta de que el t¶ermino de
la aceleraci¶on normal va siendo m¶as peque~no, y por tanto la fuerza
centr¶³peta tambi¶en. >C¶omo se logra esto?. Como el peso es constante
s¶olo se puede lograr disminuyendo la fuerza que ejerce la normal. Cuando
la fuerza centr¶³peta sea igual que el peso del cuerpo tendremos que en
este instante la normal es cero. >Y si es menor la fuerza centr¶³peta que
el peso?. Entonces deber¶³amos tener una normal positiva, es decir, que
empujara" hacia arriba. Pero esto es imposible, porque claramente se ve
que las super¯cies no absorben" los cuerpos, que es lo que supondr¶³a que
la normal tuviera signo contrario. Por lo tanto si mv2
R < mg el cuerpo no
puede rotar correctamente y caer¶³a sali¶endose del bucle. Intuitivamente
sucede que, como la fuerza centr¶³peta no necesita tanto peso, sobra
componente vertical" y, por tanto, el cuerpo cae.
As¶³ pues deducimos que la velocidad l¶³mite con la que debe llegar el
R = mg ) v = pgR.
cuerpo arriba es tal que mv2

Por ¶ultimo, para relacionar esta velocidad con la altura utilizamos el
teorema de conservaci¶on de la energ¶³a, ya que no hay rozamientos. As¶³
EA
EA
c + p = 0 + mgh
EB
p = 1
c + EB
2mv2 + 2mgR
¾
) mgh =
1
2
m
³p
gR
´2
+ 2mgR
y con un simple c¶alculo se obtiene que
h =
5
2
R:
Aunque entender intuitivamente de donde sale este 1
2R m¶as de lo
que parece que se necesita para llegar al punto m¶as alto del bucle no
es sencillo, si puede intentarse pensando que, al llegar a la parte m¶as
alta del bucle se requiere un m¶³nimo de energ¶³a cin¶etica para seguir
desplaz¶andose hacia la derecha, pero la su¯ciente para que el cuerpo
siga girando. Este m¶³nimo lo proporciona esa altura extra.

Cap¶³tulo 7
Consideraciones energ¶eticas
7.1. Introducci¶on
Los conceptos de trabajo y energ¶³a son de gran importancia en f¶³sica, y tambi¶en
son muy utilizados en la vida cotidiana. No obstante el uso habitual de estos con-ceptos
en la vida diaria no siempre coincide con su idea f¶³sica, por lo que habr¶a que
tratar la intuici¶on con cierto cuidado cuando la apliquemos a las situaciones en las
que intervienen el trabajo y la energ¶³a.
7.2. Trabajo
Se de¯ne trabajo como
W =
Z
~F ¢ d~r: (7.1)
La unidad del trabajo es el Julio. Un Julio equivale a un Nm. Si la fuerza
aplicada es constante, entonces se puede decir que
W = ~F ¢ ~r = Fr cos ®; (7.2)
en donde ® es el ¶angulo que existe entre la l¶³nea de aplicaci¶on de la fuerza y el
desplazamiento del cuerpo.
¦ Se tiene as¶³ que una fuerza aplicada perpendicularmente a un despla- Nota
zamiento no produce trabajo. Por ejemplo, avanzar horizontalmente mientras
se sujeta una bolsa no produce trabajo, porque la fuerza aplicada es vertical
y, por tanto, perpendicular al desplazamiento. >C¶omo se puede entender esto
intuitivamente?. Realmente uno asocia la palabra trabajo con cansancio" y,
por tanto, parece que llevar una pesada bolsa deber¶³a producir trabajo f¶³sico,
porque cansa. Para entender esta situaci¶on podemos pensar que realmente no
es necesario sujetar personalmente la bolsa a cierta distancia del suelo, puesto
que esta misma acci¶on puede realizarla un soporte con ruedas, por lo que el
trabajo aut¶entico consiste en desplazar el objeto paralelamente a las fuerzas
que se oponen a ¶el, como podr¶³a ser en este caso el rozamiento del soporte con
el suelo.
P >Cu¶anto es el trabajo que produce la normal sobre un cuerpo que Problema
realiza un desplazamiento sobre una super¯cie cualesquiera?
R Ninguno, porque la fuerza normal siempre es perpendicular al
desplazamiento del cuerpo y por tanto, el trabajo (producido por la Resolucio¶n
normal) ser¶a nulo.
39

CAP¶ITULO 7. CONSIDERACIONES ENERG¶ETICAS
Ahora bien. >C¶omo podemos de¯nir el trabajo si la fuerza es variable, o si la
trayectoria es curva?. En ese caso suponemos v¶alida la de¯nici¶on de trabajo para
una trayectoria muy peque~na (in¯nit¶esima) y sumamos (integramos) a todos los
peque~nos trozos de trayectoria".
Es decir:
W2 ¡W1 =
Z 2
1
~F ¢ d~r (7.3)
Problema P Un nin~o arrastra un trineo durante 100 metros. Para hacerlo tira
de una cuerda con una fuerza de 80 Newton formando un ¶angulo con el
suelo de 30o. >Cu¶al es el trabajo producido?
Resolucio¶n R Utilizando la fo¶rmula (7.2) tenemos simplemente que:
W = 80 ¢ 100 cos 30 = 6928;20J
Recuerda . Las de¯niciones de trabajo son:
W =
Z
~Fd~r
W = ~F ¢ ~r = Fr cos ®
7.2.1. Trabajo conservativo
Trabajo conservativo es aquel producido por las fuerzas conservativas. Una fuer-za
es conservativa si el trabajo que realiza no depende del recorrido sino s¶olo de
los puntos inicial y ¯nal, es decir, independientemente del itinerario seguido. Si un
cuerpo se desplaza desde un punto A hasta otro B bajo la acci¶on de una fuerza con-servativa
el trabajo realizado por dicha fuerza ser¶a el mismo independientemente
del itinerario del cuerpo.
Estas fuerzas son muy importantes porque para ellas se puede de¯nir una mag-nitud
denominada energ¶³a potencial (ver 7.5.2). Ejemplos de fuerzas conservativas
son las fuerzas constantes (aquellas cuyo valor es el mismo para todos los puntos
del espacio) y centrales (las que presentan la forma funcional f(~r) = f(r)^r).
Recuerda . Trabajo conservativo es aqu¶el que so¶lo depende de los puntos inicial
y ¯nal de la trayectoria.
7.3. Potencia
La potencia se de¯ne como el trabajo realizado por unidad de tiempo, es decir
P =
dW
dt
(7.4)
donde, si el trabajo es constante, se puede expresar como
P =
W
t
; (7.5)
y si la fuerza es constante se puede decir que
P = ~F ¢ ~v: (7.6)
La unidad de la potencia es el Watt o Vatio. (W).

Recuerda . Potencia es el trabajo realizado por unidad de tiempo.
¦ La magnitud potencia puede servir para entender algunas situaciones de Nota
la vida cotidiana. Por ejemplo los motores de los coches (suponiendo que la
presi¶on que se ejerce sobre el acelerador es constante) desarrollan una potencia
que podemos considerar constante. Esto supone que, como se deduce de la
f¶ormula (7.6) la fuerza que puede desarrollar el motor multiplicada por la
velocidad es constante. >Qu¶e podemos explicar con esto?. Supongamos que
un autom¶ovil est¶a ascendiendo por un puerto, y por tanto su motor debe de
realizar una fuerza bastante considerable para contrarrestar la componente
del peso que tira de ¶el hacia atr¶as". El conductor se ve obligado a ir en una
marcha corta, lo cual signi¯ca que la relaci¶on entre la fuerza y la velocidad va
a ser de mucha fuerza frente a poca velocidad. El mismo conductor en cambio,
en un llano, puede ir en una marcha muy larga y a gran velocidad, porque
la fuerza que debe desarrollar el motor es poca, ¶unicamente para vencer los
rozamientos.
Si este conductor es adelantado por un coche de gran potencia ver¶a como,
efectivamente, si la potencia es mayor, el coche que le adelante puede desarro-llar
la misma fuerza que se necesita para ascender por el puerto, pero a una
velocidad mayor.
P Calcula la potencia que debe tener una bomba de agua para as- Problema
cender mil litros de agua por minuto a una altura de 10 metros.
R Primero calculemos el trabajo que debe realizar esta bomba para
ascender este agua. Usando la fo¶rmula para fuerzas constantes y notando Resolucio¶n
que la fuerza que debe realizar la bomba es paralela al desplazamiento
y de m¶odulo igual al peso del agua que ha de ascender tendremos que,
W = Fd = 1000 ¢ 9;8 ¢ 10 cos 0 = 9;8 ¢ 104J:
Aplicando ahora la ecuaci¶on de la potencia (7.5) tendremos que
P =
9;8 ¢ 104
60
= 1;6 ¢ 103W:
7.4. Energ¶³a
Se considera t¶acitamente la energ¶³a como la capacidad para hacer un trabajo, o
bien el trabajo acumulado" por un cuerpo.
El concepto de energ¶³a es uno de los m¶as fruct¶³feros de toda la f¶³sica, pero
tambi¶en es bastante abstracto, dada la gran diversidad de formas en las que aparece,
por ello iremos viendo algunas, aunque antes necesitaremos de¯nir unos conceptos
previos.
7.5. Conceptos previos
7.5.1. Energ¶³a cin¶etica
Energ¶³a cin¶etica es la que tiene un cuerpo por desplazarse a determinada velo-cidad.
Realmente resulta un poco sorprendente que un cuerpo, por el mero hecho
de moverse, tenga un tipo de energ¶³a, pero no tenemos m¶as que pensar que efecti-vamente,
en caso de un choque, por ejemplo, este cuerpo es capaz de producir un
trabajo (de deformaci¶on, o del tipo que sea) y por tanto, debe de tener una energ¶³a.

Se puede demostrar la existencia de la energ¶³a cin¶etica de varias formas. Una
manera (que se deja como ejercicio al lector) es suponer que se est¶a aplicando una
fuerza constante sobre un cuerpo y que, por tanto, utilizando la ley de Newton
F = ma, tendremos un cuerpo sometido a una aceleraci¶on constante y, usando las
ecuaciones del movimiento, relacionar la cantidad trabajo, que ser¶a ma¢x con la
velocidad.
Otra forma es calcular el trabajo que desarrolla un cuerpo sometido a una cierta
fuerza paralela (para simpli¯car el c¶alculo) del tipo que sea. Utilizando (7.3) tenemos
que
W =
Z 2
1
F dx =
Z 2
1
madx
=
Z 2
1
m
dv
dt
dx =
Z 2
1
m
dx
dt
dv
=
Z 2
1
mv dv =
1
2
mv2
2 ¡
1
2
mv2
1:
Con lo cual se puede ver que el trabajo se acumula" en forma de energ¶³a cin¶etica
cuya f¶ormula es
Ec =
1
2
mv2 (7.7)
Recuerda . Energ¶³a cin¶etica es la energ¶³a que tiene un cuerpo por desplazarse
con cierta velocidad y su valor es
Ec =
1
2
mv2:
Nota ¦ En algunos libros de f¶³sica se denomina a la energ¶³a cin¶etica como T.
Es m¶as correcto expresarlo como
W2 ¡W1 =
1
2
mv2
2 ¡
1
2
mv2
1; (7.8)
¶este es el llamado teorema de las fuerzas vivas.
Para resolver un problema utilizando este teorema habr¶a que elegir unos instan-tes
1 y 2 y, calculando el trabajo y la energ¶³a en cada uno de estos instantes, el teo-rema
nos permitir¶a relacionar una de estas magnitudes con el resto. Generalmente
se busca una velocidad y se tiene el resto de datos. Hay que elegir convenientemente
los puntos 1 y 2 para obtener lo que deseamos y, adem¶as, intentar que el m¶aximo
n¶umero de estas magnitudes sea nulo, lo cual facilita el c¶alculo.
Problema P Se aplica una fuerza horizontal de 100N a un cuerpo de 2kg que
est¶a inicialmente en reposo. >A qu¶e velocidad se mover¶a al cabo de 20
metros?.
Resolucio¶n R Apliquemos el teorema de las fuerzas vivas (7.8) a este problema
y tendremos que
W = Ef
c ¡ Ei
c
siendo i y f los instantes inicial y ¯nal, respectivamente. Vemos que, en
este caso, Eic
es nula, porque el cuerpo parte del reposo, y que el trabajo
ser¶a, como la fuerza es paralela al desplazamiento, W = Fd = 100 ¢20 =
2000J. Tendremos entonces que
2000J =
1
2
mv2

y por tanto
v =
s
2
2000J
2kg
= 44;72
m
s
:
7.5.2. Potencial
La energ¶³a potencial es aquella relacionada con fuerzas conservativas. Se de¯ne
la energ¶³a potencial en un punto de tal forma que se cumpla
WAB = Ep(A) ¡ Ep(B) (7.9)
.
Igualmente, uni¯cando las de¯niciones (7.3) y (7.9) se puede decir que
W =
Z
~F ¢ d~s = ¡¢Ep (7.10)
es decir, el trabajo realizado por una fuerza conservativa equivale a la disminuci¶on
de la energ¶³a potencial, donde hemos llamado ¢Ep = Ep2 ¡ Ep1.
Es muy importante darse cuenta de la aparici¶on del signo ¡ en la f¶ormula (7.10),
consecuencia de la de¯nici¶on (7.9) anterior. Dicho signo aparece tambi¶en en las
ecuaciones (7.11), (7.12), (7.13), y (7.14).
¦ Otra notaci¶on para la energ¶³a potencial es, en vez de llamarla Ep, deno- Nota
minarla U.
¦ Intuitivamente la energ¶³a potencial es la que tiene un cuerpo por el mero
hecho de ocupar una determinada posicio¶n en el espacio. As¶³ por ejemplo, ve- Nota
remos m¶as adelante, concretamente en 7.5.2, que un cuerpo que se encuentre
a una cierta altura h sobre la super¯cie terrestre presenta, s¶olo por este hecho,
una energ¶³a potencial. Podemos entender esto d¶andonos cuenta de que, efecti-vamente,
un cuerpo, por el mero hecho de estar elevado respecto al suelo, tiene
energ¶³a, puesto que puede caer al suelo y, por tanto, desarrollar un trabajo
durante su ca¶³da.
Gravitatoria en la super¯cie terrestre
Aplicando la de¯nici¶on de potencial indicada en (7.10) tendremos que
Ep = ¡
Z y
0
m(¡g)ds = mgy (7.11)
Se tiene que
Ep = mgy
siendo y la altura sobre el suelo o el nivel 0. En la integral aparece (-g) ya que
el sentido de la fuerza de la gravedad es contrario al sentido en que se toman las
alturas.
. La energ¶³a potencial cuando el valor de g se puede tomar constante Recuerda
es
Ep = mgh:

Gravitatoria general
Como se puede ver m¶as ampliamente en (11.1) todos los cuerpos se atraen entre
s¶³ con una fuerza que se rige por la ley de Newton de la gravitaci¶on universal, es
decir, que el m¶odulo de la fuerza de atracci¶on es
F = ¡G
Mm
r2 ;
en donde el signo ¡" nos informa de que el sentido siempre es de atracci¶on.
As¶³ pues para calcular la energ¶³a potencial que un cuerpo de masa m tiene por
estar a una distancia r de otro de masa M no habr¶a m¶as que calcular
Ep = ¡
Z
F dr = ¡
Z
¡G
Mm
r2 dr = ¡GMm
Z
¡
1
r2 dr = ¡G
Mm
r
: (7.12)
Recuerda . Energ¶³a potencial gravitatoria (en el caso general) es
Ep = ¡G
Mm
r
:
Nota ¦ Tanto en esta fo¶rmula como en la fo¶rmula (7.14) un ana¶lisis del signi¯-
cado estas expresiones y, m¶as concretamente, de la presencia de una r en el
denominador, nos indica que, para estas dos f¶ormulas, el origen de las energ¶³as
se toma en el in¯nito, es decir, que la energ¶³a potencial de un planeta (por
ejemplo) es nula, cuando este planeta est¶a totalmente aislado, es decir, in¯ni-tamente
alejado, del otro.
El¶astica
Para muelles y sistemas de fuerzas centrales que cumplan ~F = ¡k~r se tiene que,
(tomando una ¶unica dimensi¶on)
Ep = ¡
Z
Fdx = ¡
Z
¡kx dx =
1
2
Kx2 (7.13)
Recuerda . La energ¶³a potencial de un sistema que obedece a la ley de Hooke
es
Ep =
1
2
Kx2:
Electrost¶atica
Dadas dos part¶³culas con cargas q y Q, se comenta en el apartado 12.1 como el
m¶odulo de la fuerza de atracci¶on entre ambas cargas es
F = K
Qq
r2 ;
siendo r la distancia que existe entre ambas cargas. De esta forma se puede extraer
f¶acilmente que la energ¶³a potencial electrost¶atica ser¶a
Ep = ¡
Z
Fdr = ¡
Z
K
Qq
r2 dr = KQq
Z
¡dr
r2 = K
Qq
r
(7.14)
Recuerda . Energ¶³a potencial entre dos part¶³culas cargadas es
Ep = K
Qq
r
:

7.6. Conservaci¶on de la energ¶³a
Cuando en un sistema s¶olo aparecen fuerzas conservativas, se tiene entonces que
se cumple el siguiente teorema de conservaci¶on de la energ¶³a
Ep(A) + Ec(A) = Ep(B) + Ec(B) (7.15)
Siendo A y B dos momentos cualesquiera en la evoluci¶on de la part¶³cula, y Ep(A)
y Ep(B) la suma de todas las energ¶³as potenciales que tenga el cuerpo en los puntos
A y B.
Este teorema es muy ¶util para la resoluci¶on de ciertos aspectos de los problemas,
sobre todo los relacionados con la obtenci¶on de la velocidad en determinados instan-tes
en un sistema conservativo. Esto se debe a que, por ejemplo, en un movimiento
sin rozamientos de un cuerpo bajo el campo gravitatorio terrestre en super¯cie,
particularizando (7.15) tenemos
1
2
mv2
1 + mgy1 =
1
2
mv2
2 + mgy2
de donde podremos despejar f¶acilmente la velocidad en uno y otro instante seg¶un
los datos que conozcamos.
. El teorema de conservaci¶on de la energ¶³a dice que la energ¶³a total Recuerda
en todos los instantes es la misma, siendo la energ¶³a total la suma de las
energ¶³as cin¶eticas m¶as las potenciales.
P Un cuerpo desliza sin rozamiento por una pista de hielo. Si parte Problema
del reposo desde una altura de 7 metros sobre el suelo. >A qu¶e velocidad
estar¶a cuando se encuentre tan s¶olo a 1 metro sobre el suelo?
R Llamemos A al instante inicial, en que encuentra parado y a 7 Resoluci¶on
metros, y B al segundo instante, cuando viaja a una velocidad v y se
encuentra a tan s¶olo 1 metro. Tendremos entonces que
EA
p + EA
c = EB
p + EB
c
p = mg7, EB
p = mg1, como parte del reposo EA
c = 1
en donde EA
2mv2 = 0
porque vA = 0 y denominando vB a la velocidad cuando pasa por el
punto B tendremos que EB
c = 1
2mv2B
. Tendremos entonces que
mg7 = mg1 +
1
2
mv2B
) v =
p
2g(7 ¡ 1) ¼ 10;84
m
s
:
7.6.1. Rozamiento
En el caso de que exista rozamiento u otras p¶erdidas de energ¶³a no conserva-tivas
podremos a¶un seguir usando (7.15) siempre que tengamos la precauci¶on de
introducir esta energ¶³a perdida por rozamiento con el signo oportuno. Por ejemplo
si tenemos un problema en el cual aparece la energ¶³a potencial en la super¯cie te-rrestre
mgh y tambi¶en una fuerza de rozamiento podr¶³amos plantear la ecuaci¶on de
conservaci¶on de la energ¶³a entre los instantes 1 y 2 como
1
2
mv2
1 + mgy1 =
1
2
mv2
2 + mgy2 + E¤;
donde se ha representado por E¤ la energ¶³a que se ha perdido entre dichos instantes.


A
B
h
a
m
m
v=0
v=?
g
Figura 7.1: A qu¶e velocidad llegar¶a al ¯nal?.
. Cuando aparezcan trabajos procedentes de fuerzas no conservativas Recuerda
los puedes poner como
c + EA
p = EB
c + EB
p + E¤ (7.16)
EA
Donde E¤ es el trabajo no conservativo.
A su vez el trabajo de rozamiento puede calcularse teniendo presente que W =
Fd cos ® y que ® = 180o porque el rozamiento siempre se opone al desplazamiento.
De esta forma se tendr¶³a que W = ¡¹Ngs pero, como el t¶ermino E¤ se sit¶ua en el
miembro derecho de la ecuaci¶on (7.16) con valor positivo, simplemente
E¤ = ¹Ns;
donde N es la normal y s es el desplazamiento que ha realizado el cuerpo, es decir,
la distancia durante la cual ha experimentado el rozamiento.
Problema P Dejamos caer desde el reposo un cuerpo de masa m por una rampa
de ® grados de inclinaci¶on desde una altura h (ver ¯gura 7.1). Si la rampa
ofrece un coe¯ciente de rozamiento ¹. A qu¶e velocidad llegar¶a al suelo?
Resolucio¶n R Planteemos la ecuacio¶n de conservacio¶n de la energ¶³a expresada
en (7.16) y analicemos el valor de cada t¶ermino. Antes llamaremos A al
instante en el cual el cuerpo se encuentra a cierta altura h y B cuando
el cuerpo est¶a ya al nivel del suelo con una velocidad v. As¶³ tendremos
que
EA
p = mgh
EB
p = mg0 = 0
EA
c =
1
2
m02 = 0
EB
c =
1
2
mv2
E¤ = ¹Ns
Donde queda por precisar que s es el espacio total recorrido por el cuerpo
mientras bajaba por la rampa. Teniendo en cuenta que el espacio s es

la hipotenusa de un tri¶angulo rect¶angulo donde un ¶angulo mide ® y su
lado opuesto mide h, se tiene que s = h
sin ®.
Respecto a la normal N, como se ha visto ya en 6.6, su valor ser¶a N =
mg cos ® por lo que el valor de E¤ en funci¶on de par¶ametros conocidos
ser¶a
E¤ = ¹mg cos ®
h
sin ®
.
Por ¯n utilizando (7.16) tenemos que
mgh =
1
2
mv2 + ¹mg cos ®
h
sin ®
y despejando v se obtiene la soluci¶on, que es,
v =
p
2gh (1 ¡ ¹ tan ®¡1):
± Como consecuencia del problema anterior Para qu¶e relaci¶on entre ¹ y Ampliaci¶on
® el cuerpo no podr¶³a bajar por la rampa?.
7.7. Impulso
El impulso surge de integrar la fuerza respecto al tiempo.
~I =
Z
~Fdt: (7.17)
O lo que es lo mismo,
¢~p = ~p2 ¡ ~p1 = I2 ¡ I1 =
Z
~Fdt:
7.8. Gradiente
± Sabiendo que podemos expresar un incremento in¯nitesimal de energ¶³a Ampliaci¶on
potencial como
dEp = Ep(~r + d~r) ¡ Ep(~r) = ¡~F ¢ d~r = ¡(Fxdx + Fydy + Fzdz)
y que la regla de derivaci¶on de la cadena para varias dimensiones nos dice que
dEp =
@Ep
@x
dx +
@Ep
@y
dy +
@Ep
@z
dz
tenemos entonces una interesante relaci¶on1 que nos dice que
Fx = ¡
@Ep
@x
Fy = ¡
@Ep
@y
Fz = ¡
@Ep
@z
9=
;:
A ra¶³z de esto se puede de¯nir matem¶aticamente el gradiente de un escalar
como nabla por dicho escalar. Por nabla se de¯ne al vector2 ~r
= @
@x^{+ @
@y ^|+
@
@z
^k. La notaci¶on @f
@x supone derivar la funci¶on f respecto a la variable x y
considerar el resto de variables, (y, z, etc.) como si fueran constantes.
1Mucho m¶as explotada en libros de f¶³sica m¶as avanzados
2Pues realmente es un operador, ya que act¶ua como una derivaci¶on sobre los escalares o vectores
a los que se le aplica.

Con esto podemos de¯nir el vector fuerza como
~F = ¡~r
Ep (7.18)
Las propiedades matem¶aticas del gradiente son muy interesantes, aunque
exceden ampliamente el nivel de este libro.

Cap¶³tulo 8
Din¶amica de un sistema de
part¶³culas
8.1. Conceptos y de¯niciones primarias
Sistema de part¶³culas es un conjunto de part¶³culas1 cuyas propiedades globales
queremos estudiar.
Fuerza exterior de un sistema de part¶³culas es aquella que viene de fuera del siste-ma.
Fuerza interior es la proveniente de las interacciones entre las propias part¶³culas
del sistema. Se pueden denotar como ~Fext y ~Fint.
8.2. Centro de masas
El centro de masas para un sistema de part¶³culas discreto es
~rcm =
m1~r1 + m2~r2 + :::
m1 + m2 + :::
=
PN
i=1mi~ri PN
i=1mi
: (8.1)
Cuando se tenga un sistema continuo el centro de masas vendr¶a de¯nido como
~rcm =
R
R~r dm
dm
o, expres¶andolo mejor en funci¶on de la densidad del sistema
~rcm =
R
½dm
mT
siendo mT la masa total del cuerpo continuo.
8.2.1. Teorema de Pappus
± Este teorema resulta muy ¶util para calcular el centro de masas de Ampliaci¶on
algunas ¯guras. El mecanismo de funcionamiento es como sigue: tomando
un ¶area cualquiera cerrada en un plano y generando un s¶olido rot¶andola en
el espacio de manera tal que cada punto siempre se mueva perpendicular al
plano del ¶area, tendremos como resultado que el s¶olido as¶³ generado tendr¶a un
volumen igual que el ¶area de esta secci¶on empleada por la distancia que se ha
desplazado el centro de masas.
1Supuestas puntuales.
49

CAP¶ITULO 8. DIN¶AMICA DE UN SISTEMA DE PART¶ICULAS
8.3. Din¶amica del centro de masas
8.3.1. Velocidad
Hallar la magnitud ~vcm es simplemente derivar la ecuaci¶on (8.1), con lo cual se
llega a
~vcm =
1
mT
XN
i=1
~pi
o, tambi¶en se tiene
mT ~rcm =
XN
i=1
~pi: (8.2)
8.3.2. Aceleraci¶on
Derivando dos veces
~Fext = mt~acm: (8.3)
Para llegar a este resultado ha hecho falta darse cuenta de que cada ~Fi = mi~ai
se puede descomponer en ~Fi = ~Fext
i + ~Fint
i donde ~Fint
i =
PN
j6=i
~Fij , siendo estas ~Fij
todas las fuerzas de interaccion ¶entre las part¶³culas o, mas ¶concretamente, la fuerza
que una part¶³cula j ejerce sobre la i. Posteriormente cuando Pse suman todas estas
fuerzas en la formula ¶general se tiene que el sumatorio
N
i
PN
j6=i
~Fij se anula ya
que, por el principio de acci¶on y reacci¶on, ~Fij = ¡~Fji.
8.3.3. Momento lineal
Se de¯ne el momento lineal de un sistema de part¶³culas como la suma de los
momentos de cada una de las part¶³culas que integran el sistema. Quiere decir esto
que el momento lineal de un sistema ser¶a
~p
XN
i=1
~pi:
Atendiendo a la f¶ormula (8.2) podemos ver claramente que
~p = mt~vcm:
A su vez, si la fuerza exterior ejercida sobre el sistema de part¶³culas es nula,
haciendo uso de (8.3) se ve f¶acilmente que ~p permanece constante, de donde podemos
enunciar la conservaci¶on del momento lineal total del sistema:
~Fext = 0 ) ~p = cte:
Recuerda . Si la fuerza neta externa que actu¶a sobre un sistema es nula, el
momento lineal de ¶este se conserva.
8.3.4. Energ¶³a
Generalizando el teorema de las fuerzas vivas a todo un sistema de part¶³culas se
puede demostrar que
WA!B
t = Ec(B) ¡ Ec(A)

donde Ec =
PN
i=1 Ec;i. Cuando todas las fuerzas, tanto las internas como las exter-nas,
que aparecen en acci¶on en el sistema son conservativas podemos enunciar un
teorema general de conservaci¶on de la energ¶³a, que dir¶a
ET = Ec + Ep = cte:
Ahora bien, como ya hemos de¯nido una Ec total nos quedar¶a ver c¶omo de¯nir la
magnitud Ep. Intuitivamente se puede ver que deber¶a ser una suma de todas las
energ¶³as potenciales puestas en juego en el sistema, es decir, un t¶ermino donde se
considere la energ¶³a potencial que pueda tener cada part¶³cula por la aplicaci¶on de la
fuerza externa, y otro donde se sumen todos los pares de interacci¶on entre part¶³culas
del propio sistema, que tambi¶en contribuir¶a. Estas ideas se traducen en
Ep =
XN
i=1
Eext
p;i +
1
2
XN
i=1
Xn
j6=i
Eint
p;ij :
Energ¶³a mec¶anica interna
Relacionando la energ¶³a cin¶etica de un sistema de part¶³culas en un sistema de
referencia inercial usual con la que tiene en el sistema de referencia centro de masas
se llega a la ecuaci¶on
Ec = E0c
+
1
2
mtv2
cm
donde vemos que, adem¶as de la energ¶³a cin¶etica que tiene el sistema consider¶andole
como un ¶unico cuerpo situado en su centro de masas, aparece otra energ¶³a, que se
relaciona con c¶omo se mueven esas part¶³culas respecto al centro de masas.
c se puede expresar mucho m¶as f¶acil- Nota
¦ Posteriormente veremos que esa E0
mente cuando tenemos un sistema de masas continuo que esta rotando
. Cuando tanto las fuerzas externas como las internas que act¶uan
sobre un sistema de part¶³culas son conservativas, la energ¶³a total del Recuerda
sistema permanece constante.
8.4. Aplicaciones
8.4.1. Sistema de referencia del centro de masas
Consiste en situar el sistema de coordenadas justo con el origen en el centro
de masas. Tiene como ventaja que, si la resultante de todas las fuerzas exteriores
es nula, es decir si ~Fext = ~0, entonces en este nuevo sistema el centro de masas
permanece constante e igual a 0 (ya que est¶a situado en el origen de coordenadas)
y adem¶as, se trata de un sistema inercial.
Para pasar de un sistema a otro basta usar las ecuaciones (5.3) en este caso
particular y tendremos
~r0i
= ~ri ¡~rcm
~v0i
= ~vi ¡~vcm
habiendo primado en este caso las coordenadas que se ver¶³an desde el sistema centro
de masas.

8.4.2. Problemas de dos cuerpos
± Cuando tenemos un problema de dos cuerpos podemos separar este Ampliaci¶on
problema en dos situaciones diferenciadas. Por ejemplo, si queremos ver que
sucede con el sistema Tierra-Sol, podr¶³amos plantearnos usar la ecuaci¶on (8.3)
para tener una idea global de c¶omo se est¶a moviendo el sistema.
No obstante esta ecuaci¶on no nos da la informaci¶on concreta de c¶omo una
part¶³cula, o un planeta, se mueve respecto al otro, sino s¶olo como se desplaza
su centro de masas. Es muy ¶util suponer que las fuerzas exteriores sobre el
sistema sean nulas, es decir, que tengamos un sistema de dos cuerpos aislados,
y ver que sucede. En ese caso ~acm = ~0 y, por tanto, el c.d.m. se desplazar¶a con
movimiento rectil¶³neo y uniforme (o se estar¶a quieto). Pero qu¶e sucede con
las part¶³culas que componen nuestro sistema?.
Cuando las fuerzas externas son nulas se puede demostrar tras un poco de
¶algebra que
~F12 = ¹~a12
donde ¹ = m1m2
m1+m2
y ~a12 es la aceleraci¶on del cuerpo 2 vista desde el 1. Esta
igualdad nos permitir¶³a establecer como es el movimiento de los cuerpos como
si de un ¶unico cuerpo de masa ¹ se tratase.
8.4.3. Colisiones
Cuando tenemos un sistema de part¶³culas en el cual sus part¶³culas componentes
chocan entre s¶³, en ausencia de fuerzas externas, hemos de tener en cuenta que
esto supone una conservaci¶on de la masa, evidentemente, m¶as una conservaci¶on del
momento lineal, como ya se ha escrito en 8.3.3. Por tanto tomando el sistema en un
instante inicial y otro final tendremos
P
imii
=
P
imf
P i
i pii
=
P
pf
i i
En general, para simpli¯car los problemas, el n¶umero de part¶³culas en los ins-tantes
i y f suele ser 1 o 2.
Conservaci¶on de la energ¶³a
En las colisiones, en cambio, no se tiene por qu¶e conservar la energ¶³a. Aquellas
en las que si que se tiene que Eic
= Ef
c se denominan el¶asticas. Para medir el grado
de elasticidad de una colisi¶on, y tambi¶en para aportar un dato extra en el caso
en el cual la conservaci¶on del momento (y de la masa) no nos aporta informaci¶on
su¯ciente, se recurre al concepto de coe¯ciente de restituci¶on. ¶Este se de¯ne en el
caso unidimensional como
K = ¡
vf
1 ¡ vf
2
vi2
¡ vi2
(8.4)
y cuyo valor var¶³a entre 1 para un choque el¶astico y 0 para otro perfectamente
inel¶astico.
Ampliacio¶n ± La demostracio¶n de que K = 1 para un choque ela¶stico no es complicada,
aunque hay que hacer un poco de ¶algebra. Pasa simplemente por plantear, para
un choque de dos cuerpos donde no hay variaci¶on en la masa, las ecuaciones de
conservaci¶on del momento lineal y, por ser el¶astico, tambi¶en las de la energ¶³a
cin¶etica. Ser¶an dos ecuaciones con dos inc¶ognitas. Se despeja y sustituye y, al
resolver la ecuaci¶on de segundo grado que se obtiene, sale una relaci¶on de vf
1
y vf
2 de la cual ya, introduciendo sus valores en (8.4) se obtiene el resultado
deseado. Ser¶³a muy ¶util que el lector comprobara esto personalmente a modo
de ejercicio pr¶actico.

Cap¶³tulo 9
Din¶amica de la rotaci¶on
9.1. Introducci¶on
9.1.1. S¶olido r¶³gido
Para simpli¯car mucho la explicaci¶on de la rotaci¶on en los cuerpos se toma siem-pre
un modelo de c¶omo son estos cuerpos que se denomina s¶olido r¶³gido. Este modelo
consiste en considerar que los cuerpos, los s¶olidos tomados, son absolutamente in-deformables,
son r¶³gidos. Matem¶aticamente se puede expresar de una manera m¶as
rigurosa diciendo que la distancia entre sus part¶³culas no cambia. Dada una part¶³cu-la
j y otra i del sistema que consideremos siempre se tendr¶a que j~ri ¡~rj j = K siendo
K una constante cualesquiera.
Para un cuerpo de este tipo, por tanto, conociendo d¶onde est¶a en un momento
determinado una part¶³cula y el ¶angulo µ de rotaci¶on del cuerpo respecto a la posici¶on
original, conocemos el resto de las posiciones de los puntos.
9.1.2. Analog¶³as
El estudio de la din¶amica de la rotaci¶on se puede hacer sencillo teniendo presentes
las siguientes analog¶³as entre la din¶amica normal y ¶esta.
traslaci¶on Rotaci¶on
x µ
v !
a P
®
m I =
mir2
ii
~p ~L
= ~r ^ ~p
~F ~M
= ~r ^ ~F
F = ma M = I®
F = dp
dt M = dL
dt
p = mv L = I!
W = Fd W = Mµ
Ec = 1
2mv2 Ec = 1
2 I!2
9.2. Momento de una fuerza
Cuando un cuerpo sufre una aceleraci¶on es porque tiene una causa que lo pro-voca.
Newton descubri¶o que es la fuerza la causa de que esto suceda. Cu¶al es la
causa de una rotaci¶on?. Es el momento de una fuerza. Una deducci¶on f¶acil, clara y
divertida se puede encontrar en [1]. De momento aqu¶³ se expondr¶a su de¯nici¶on y
53

CAP¶ITULO 9. DIN¶AMICA DE LA ROTACI ¶ON
propiedades. Como ~M
= ~r ^ ~F tomando M ser¶a igual a rF sin ® siendo ® el ¶angulo
formado entre el vector ~r y ~F. Por tanto la componente perpendicular al vector
posici¶on es la que interviene realmente en la rotaci¶on.
Recuerda . La componente de la fuerza perpendicular al vector posicio¶n es la
que realmente interviene en la rotaci¶on.
9.3. Momento angular
En din¶amica de traslaci¶on la variaci¶on del momento lineal ~p respecto al tiempo
es denominada fuerza. Parece l¶ogico suponer que debiera existir alguna magnitud
an¶aloga en din¶amica de rotaci¶on tal que su derivada temporal nos proporcione
tambi¶en la causa, es decir, el momento de las fuerzas ~M
. Como ~M
= ~r^ ~F probemos
a tomar ~M
= d~L
dt siendo
~L
= ~r ^ ~p (9.1)
y ver que sucede al ser derivado. Es sencillo llegar a la conclusi¶on de que, efecti-vamente,
esta magnitud es la an¶aloga del momento lineal ~p en cuanto que al ser
derivada se obtiene ~M
.
Ampliacio¶n ± Derivar esta magnitud no es complicado, razonando que un producto
vectorial no es sino un producto combinado de las componentes de un vector
no parece descabellado admitir que
d
dt
¡
~a ^~b
¢
=
d~a
dt
^~b +~a ^
d~b
dt
As¶³ tenemos que
d
dt
(~r ^ ~p) =
d~r
dt
^ ~p +~r ^
d~p
dt
dt = ~F. Tenemos
en donde es sencillo darse cuenta de que ~p = m~v y que d~p
entonces un primer sumando que ser¶a ~v ^m~v = 0 por se el producto vectorial
de dos vectores paralelos, y un segundo sumando que es, efectivamente, igual
a ~M
.
Tambi¶en se puede expresar L en funci¶on del momento de inercia I como
L = I!:
Ampliacio¶n ± La igualdad L = I! se puede conseguir tomando un so¶lido r¶³gido y
calculando cuanto ser¶a su momento angular. Para una determinada part¶³cula
tendremos que Li = mirivi. De aqu¶³ s¶olo resulta interesante conocer cuanto
ser¶a la proyecci¶on de este valor sobre el eje z que vamos a tomar en este caso
como el eje de rotaci¶on. Esta proyecci¶on se logra multiplicando Li por el sin µi,
siendo µi el ¶angulo formado por ~ri con el eje de giro. As¶³ tenemos que
Lz =
X
i
Lzi =
X
i
mirivi sin µi =
X
i
miR2
i !
siendo Ri la distancia de la part¶³cula i al eje. Todo esto se puede expresar
ahora f¶acilmente como
Lz = !
X
i
miR2
i = Iw
puesto que se de¯ne I =
P
i miR2
i . Existen algunos ejes en un cuerpo, gene-ralmente
ejes de simetr¶³a, tales que si el cuerpo rota alrededor de estos ejes,
el momento angular total es paralelo al eje de rotaci¶on, y por tanto para ellos
Lz = L. En estos casos se puede escribir que
~L
= I~!:

¦ El momento angular total como vector ~L
Nota no tiene por qu¶e estar en la
direcci¶on del eje de rotaci¶on si este eje no coincide con alguno de simetr¶³a del
cuerpo.
9.4. Momento de inercia
Se ha visto ya en apartados anteriores la importancia relativa del momento de
inercia I como el an¶alogo de la masa para las rotaciones.
. El momento de inercia es el an¶alogo de la masa para una rotaci¶on. Recuerda
Para sistemas discretos este momento de inercia se expresa como
I =
X
i
mir2
i
donde ri representa la distancia de la part¶³cula al eje de rotaci¶on. Pero normalmente
se tiene cuerpos reales, formados por tal cantidad de ¶atomos, de peque~nas part¶³culas
que se les supone continuos. Para ellos la f¶ormula de c¶alculo del momento de inercia
es
I =
Z
r2dm =
Z
r2½dV:
No obstante, a la hora de determinar el momento de inercia de un determinado
cuerpo es interesante conocer que
1. La simetr¶³a del cuerpo permite a veces realizar s¶olo parte del c¶alculo.
2. Como el momento de inercia es aditivo1 el c¶alculo de un momento de inercia
de un cuerpo compuesto se puede tomar como la suma de los momentos de
inercia de sus partes. Tambi¶en si tenemos un cuerpo formado por uno m¶as
sencillo al que le falta un cacho podemos calcular su momento como la
suma del cuerpo sencillo menos el cacho que le falta.
3. Muchas veces dado el momento de inercia de un cuerpo respecto a un cierto
eje podemos sacar su momento en otro eje sin necesidad de recalcularlo usando
el teorema de Steiner o el de las ¯guras planas.
9.4.1. Teorema de Steiner o de los ejes paralelos
El teorema de Steiner relaciona el momento de inercia de un eje que pase por
el centro de masas de un cuerpo con el momento de inercia que tendr¶³a el mismo
cuerpo tomando cualquier otro eje paralelo al primero. Esta relaci¶on es
I = Icm + md2
donde I es el momento de inercia del cuerpo respecto al eje paralelo al original, Icm
es el momento de inercia del eje que pasa por el centro de masas, m es la masa total
del cuerpo y d es la distancia entre estos ejes paralelos.
. El teorema de Steiner relaciona el momento de inercia respecto a Recuerda
un eje que pase por el centro de masas de un s¶olido con cualquier otro
eje paralelo a ¶el.
1Ya que proviene de una suma o integraci¶on, que son operadores lineales.

9.4.2. Teorema de las ¯guras planas o de los ejes perpendi-culares.
El momento de inercia de una ¯gura plana respecto a un eje perpendicular a la
¯gura es igual a la suma de los momentos de inercia de dos ejes que est¶en contenidos
en el plano de la ¯gura, corten al eje perpendicular y sean todos perpendiculares
entre si.
z
y
x
Figura 9.1: Dibujo de una ¯gura plana.
Es decir, dado el dibujo de la ¯gu-ra
9.1 tendremos que Iz = Iy + Ix. Es-te
teorema nos sirve, por ejemplo, para
calcular f¶acilmente el momento de iner-cia
de un anillo. Respecto al eje que pa-sa
por el centro del anillo, como toda
la masa est¶a situada a la misma distan-cia
tenemos que su momento de iner-cia
ser¶a de mR2 (es trivial, como dicen
los matem¶aticos). Adem¶as como el ani-llo
tiene mucha simetr¶³a el momento de
inercia de un eje que est¶e contenido en
el plano del anillo ser¶a igual al de otro
eje tambi¶en contenido en el plano pero
perpendicular al eje anterior, ya que el anillo se ve igual. Si llamamos a este otro
momento Ip poniendo p de plano, tendremos que mR2 = Ip + Ip ) Ip = 1
mR2.
2Recuerda . El teorema de los ejes perpendiculares so¶lo se aplica a las ¯guras
planas y permite relacionar el momento perpendicular al plano de la
¯gura con los momentos de otros dos ejes contenidos en el plano de la
¯gura.
9.4.3. Relaci¶on del momento de inercia respecto a un punto
con los tres ejes
Si llamamos al momento de inercia de un cuerpo respecto a un punto, y no un
eje, I0 tendremos que
2I0 = Ix + Iy + Iz:
Como demostraci¶on basta darse cuenta que el momento I0 ser¶a
Z
(x2 + y2 + z2) dm
frente a los momentos
Ix =
R
(y2 + z2) dm
Iy =
R
(x2 + z2) dm
Iz =
R
(x2 + y2) dm
9=
;:
9.5. Ecuaci¶on de la din¶amica de rotaci¶on
Sabemos ya que dL
dt = M y que cuando la rotaci¶on es alrededor de un eje de
simetr¶³a2 L = I!. Introduciendo esta L en la f¶ormula anterior tenemos sencillamente
que
M = I® (9.2)
donde ® es la derivada de ! respecto al tiempo, es decir, ser¶a la aceleraci¶on angular.
2Lo cual ser¶a cierto en los problemas que puedan surgir a este nivel.

De esta manera la ecuaci¶on (9.2) nos proporciona una relaci¶on entre los momen-tos
aplicados a un cuerpo y la aceleraci¶on angular que logra alcanzar ese cuerpo. En
muchos casos, como se puede ver en 9.7.1 y 9.7.2 se puede establecer una relaci¶on
entre ® y ~a.
9.5.1. Conservaci¶on del momento angular
A partir de la f¶ormula (9.2) y, de manera an¶aloga a como lo planteamos con la
din¶amica de traslaci¶on, se puede establecer que cuando no act¶ua ning¶un momento
externo sobre un sistema de part¶³culas o un cuerpo r¶³gido, su momento angular se
mantiene constante, teni¶endose entonces que
Li = Lf :
¶Esta es una igualdad muy ¶util para resolver situaciones en las que el cuerpo var¶³a
su forma, y por tanto su momento de inercia I, pero sin que existan momentos
externos. Una explicaci¶on m¶as detallada se encuentra en 9.7.6.
. Cuando no act¶uan momentos externos sobre un sistema de part¶³- Recuerda
culas su momento angular L permanece constante.
9.6. Energ¶³a de rotaci¶on
Al igual que un cuerpo con una cierta velocidad v presenta una energ¶³a cin¶etica
igual a 1
2mv2, los cuerpos que rotan tienen una energ¶³a asociada a esta rotaci¶on
que, por analog¶³a, resulta ser
Ec =
1
2
I!2:
± Tambi¶en se puede razonar tomando Ec =
P
i
1
2miv2
i y, como vi = ri! Ampliaci¶on
tendremos E =
P
i
1
2mir2
i !2 que, extrayendo factor com¶un resultar¶a ser
Ec =
1
2
Ã
X
i
mir2
i
!
!2 =
1
2
I!2:
Cuando, adem¶as, el cuerpo est¶a girando con respecto a un eje que pase por su
centro de masas la energ¶³a cin¶etica total es igual a la de traslaci¶on del centro de
masas m¶as la de rotaci¶on, es decir
Ec =
1
2
mv2
cm +
1
2
Icm!2
siendo m la masa total del cuerpo y vcm e Icm la velocidad del centro de masas y
el momento de inercia del cuerpo cuando rota por un eje que pase por el centro de
masas, respectivamente.
9.7. Algunos problemas t¶³picos de rotaci¶on
Se detallan a continuaci¶on algunas situaciones f¶acilmente resolubles y carac-ter
¶³sticas en las cuales se aplican las f¶ormulas anteriores de din¶amica de rotaci¶on.

9.7.1. Cuerpos rodantes
Cuando un cuerpo rueda sin deslizarse se establece una ligadura, hablando en
lenguaje f¶³sico, entre el ¶angulo que rota el cuerpo y la distancia que avanza. Para
un cuerpo redondo, que es el caso com¶un, s = Rµ, siendo R el radio de la ¯gura.
Esto es muy l¶ogico porque si el camino que va recorriendo el m¶ovil fuera mayor que
la longitud de cuerpo que toca el suelo necesariamente deber¶³a haber alg¶un tipo de
deslizamiento.
Teniendo esta igualdad es muy f¶acil establecer que
vcm = R!
acm = R®
¾
:
9.7.2. Poleas
En problemas en los que aparezcan poleas, como ¶estas giran alrededor de su
centro de masas y su momento de inercia ser¶a el de un c¶³rculo (o un cilindro, si es
tridimensional), tendremos ya toda la situaci¶on conocida.
1. El momento de las fuerzas ser¶a simplemente el producto de la fuerza, o la
tensi¶on de la cuerda, por el radio de la polea al que se aplica.
2. El momento de inercia de un c¶³rculo es 1
2MR2.
3. Tendremos as¶³ que, si la cuerda pasa por la parte exterior de la polea, como es
habitual (hay que tener m¶as cuidado si la polea tiene m¶as gargantas o ¶estas
no est¶an sobre la super¯cie externa del disco) para cada tensi¶on T aplicada
en la polea TR = 1
2MR2®.
4. Como la cuerda gira sin deslizar existe la condici¶on a = R® que se aplica a la
ecuaci¶on anterior.
9.7.3. Est¶atica y equilibrios
En aquellos problemas en los cuales, no existiendo movimiento de ning¶un tipo,
se nos pida calcular la geometr¶³a de alguna estructura o bien las fuerzas de acci¶on o
de reacci¶on que hay que tener para mantener la estructura en equilibrio basta con
aplicar dos f¶ormulas.
1. Al no haber movimiento del centro de masas tendremos que la resultante de
todas las fuerzas deber¶a ser nula. As¶³
X
~F = 0:
Esta ecuaci¶on se descompondr¶a en tantas como dimensiones tenga el proble-ma.
2. Cuando hay una situaci¶on est¶atica o un equilibrio el cuerpo tampoco gira
respecto a ning¶un punto. Por ello podremos aplicar tambi¶en que los momentos
resultantes deben ser nulos X
~M
= 0:
Con estas ecuaciones aplicadas con cierta intuici¶on a algunos puntos concretos
del sistema se pueden resolver este tipo de problemas.

9.7.4. C¶alculo de la aceleraci¶on angular de un cuerpo
Para ello hay que aplicar la ecuaci¶on general de la din¶amica de rotaci¶on.
1. Se consigue el momento de inercia de la ¯gura respecto al eje en que se produce
la rotaci¶on.
2. Se calculan los momentos de fuerzas tomando como punto uno del eje de
rotaci¶on. Si el problema es bidimensional este eje ser¶a perpendicular al plano,
generalmente, y podremos reducir el momento de fuerzas tridimensional a su
m¶odulo, es decir M = Fc sin µ, siendo µ el ¶angulo que forman ~F con ~r.
3. Se relacionan estas magnitudes con la aceleraci¶on angular ® mediante
P
M =
I®.
9.7.5. C¶alculo de momentos de inercia
Para la resoluci¶on de los problemas de c¶alculo de momentos de inercia es habitual
el planteamiento seg¶un algunos distintos tipos.
1. Si no conocemos el momento de la ¯gura en absoluto respecto a ning¶un otro
ePje, y ¶esta no esta¶ compuesta de otras ¯guras tendremos que aplicar I =
imiR2
i para un cuerpo discreto o bien I =
R
R2dm =
R
R2½dV para uno
continuo.
2. Si la ¯gura es plana y conocemos los dos momentos de inercia del plano, y
nos piden el del eje perpendicular a la ¯gura se intenta usar el Teorema de las
¯guras planas. (Ver 9.4.2).
3. Si conocemos el momento de inercia respecto a un eje que pasa por el centro
de masas y nos piden hallar el de otro eje paralelo a este usaremos el Teorema
de Steiner. (Ver 9.4.1).
4. Si nuestra ¯gura est¶a compuesta por otras ¯guras de las cuales conocemos su
I, o bien parece una ¯gura sencilla a la que se ha extra¶³do alguna otra ¯gura
simple, usando la linealidad del momento de inercia podremos poner nuestro
momento inc¶ognita como sumas o restas de otros momentos m¶as sencillos,
teniendo siempre cuidado de que todos los momentos est¶en referidos al mismo
eje de rotaci¶on.
9.7.6. Variaci¶on de la forma del cuerpo que gira
En aquellos problemas en los cuales var¶³e la forma de un cuerpo pero no exis-tan
momentos externos es muy ¶util la aplicaci¶on del principio de conservaci¶on del
momento angular. Tomando un instante i y otro f inicial y ¯nal tendremos que
Li = Lf y, por tanto
Ii!i = If!f ;
relaci¶on de la que conocidos tres datos podremos extraer el cuarto.
¦ Esta es la raz¶on por la que las patinadoras sobre hielo, cuando encogen Nota
los brazos, van angularmente m¶as deprisa. Al disminuir su I resulta que !
debe aumentar para mantener constante el momento angular.

9.7.7. Conservaci¶on de la energ¶³a para cuerpos rodantes
Si tenemos un caso de un cuerpo sim¶etrico que rueda respecto a un eje que pasa
por su centro de masas y todas las fuerzas externas son conservativas, podremos
aplicar el teorema de conservaci¶on de la energ¶³a y tendremos que
E = Ec;1 + Ep;1 = Ec;2 + Ep;2:
En este caso adem¶as
Ec =
1
2
mv2
cm +
1
2
I!2:
Adem¶as, si el cuerpo rueda sin deslizar se podr¶a relacionar v y ! mediante v = R!.

Cap¶³tulo 10
Conceptos generales de
campos
10.1. Introducci¶on
En bastantes campos de la f¶³sica se trata el concepto de campo, introduci¶endole
de forma m¶as o menos intuitiva y formulandolo despu¶es r¶apidamente para despu¶es
realizar con ¶el algunos c¶alculos. De todas formas parece m¶as conveniente analizar
ahora algunos conceptos de manera un poco m¶as rigurosa para poder luego entender
mejor la visi¶on que sobre la f¶³sica aportan los campos.
10.2. De¯nici¶on
Se denomina campo a todo objeto matem¶atico que est¶e de¯nido para cualquier
punto del espacio. En f¶³sica una magnitud es un campo cuando est¶a de¯nida en
todo el espacio. Si esta magnitud es un n¶umero, un escalar, tendremos un campo
escalar, si es en cambio un vector, ser¶a un campo vectorial.
Por ejemplo, en un d¶³a con mucho viento, la temperatura que haga en cualquier
parte de una ciudad ser¶a un campo escalar. As¶³ podemos decir que en el punto
tal existen tantos grados de temperatura y en el cual otros ciertos grados de
temperatura. Dado cualquier punto de la ciudad diciendo que temperatura hace
tendremos un campo escalar (de temperaturas). Si para esta misma ciudad tomamos
la intensidad y direcci¶on del viento como un vector tendremos un campo vectorial.
An¶alogamente podremos decir: En este punto el vector de la velocidad del viento es
tanto, pero en este otro punto es cuanto. Tendremos de¯nida una cierta magnitud
vectorial en todos los puntos del espacio.
10.3. Formalismo matem¶atico
Para describir matem¶aticamente un campo bastar¶a con indicar cu¶anto vale la
magnitud que nos interese en todos los puntos del espacio indicada por una cierta
funci¶on. Para un campo escalar tendremos que M = f(x; y; z) o quiz¶as tambi¶en del
tiempo t. Por ejemplo, si queremos de¯nir el campo escalar distancias al origen de
coordenadas tendremos que M =
p
x2 + y2 + z2 y as¶³ hemos cumplido la de¯nici¶on
de campo escalar. Dado un punto del espacio tenemos bien escrita una magnitud
para ese punto. En el punto (1; 1; 1) la magnitud, en este caso, es p3.
Un campo vectorial se de¯ne de manera an¶aloga, pero teniendo en cuenta que
deberemos aportar las tres componentes del vector. Podemos denotarlo como ~M
=
61

CAP¶ITULO 10. CONCEPTOS GENERALES DE CAMPOS
~ f(x; y; z) o tambi¶en como
Mx = f1(x; y; z)
My = f2(x; y; z)
Mz = f3(x; y; z)
9=
;:
Un ejemplo (que representa una fuerza cualesquiera) de campo vectorial ser¶³a
~M
(x; y; z) = x2^{ + y2^| + xy^k:
10.4. Flujo de un campo vectorial
Se de¯ne el °ujo de un campo vectorial como la cantidad de campo que atraviesa
cierta ¶area. Como esta de¯nici¶on hablada es un poco pobre, matem¶aticamente si
tenemos un campo vectorial ~M
que atraviesa una peque~na regi¶on dS tomamos
como dÁ = MdS. Ahora bien, no es lo mismo que la super¯cie que atraviese sea
perpendicular al campo, en cuyo caso entrar¶³a de lleno a que dicha super¯cie
est¶e situada de forma paralela, pues en este ¶ultimo caso no atravesar¶³a nada de
campo. Por esto se de¯ne un vector d~S
que sea perpendicular a la peque~na ¶area
considerada y tener as¶³ que dÁ = ~M
¢d~S
. Con esto logramos que aparezca el t¶ermino
cos µ en la de¯nici¶on de °ujo y poder as¶³ considerar la proyecci¶on correcta de campo
que atraviesa la super¯cie. Para lograr tener el °ujo total no hay m¶as que integrar:
ÁM =
Z
S
~M
¢ ~S
:
10.5. Gradiente de un campo
Ampliacio¶n ± Dada una fuerza conservativa ya hemos visto anteriormente como se
pod¶³a extraer de un potencial, lo cual reportaba la ventaja de que una fuerza
conservativa no es sino un campo vectorial, y por tanto tendr¶a tres dimensio-nes,
frente a un potencial, que puede ser considerado un campo escalar y por
tanto presenta s¶olo una dimensi¶on.
La operaci~r
on ¶por la cual lograbamos ¶esto la llamamos gradiente, y ten¶³a-mos
que F ~= ¡V .
As¶³ pues la operaci¶on gradiente es una forma de, a partir de un campo
escalar, lograr otro vectorial y, como hemos visto en el p¶arrafo anterior, este
campo nuevo ser¶a un campo de fuerzas si el otro era un potencial.
10.6. Ley de Gauss
Si tomamos una fuerza central que decrezca con el cuadrado de la distancia,
es decir, del tipo ~F = C br
r2 donde C es una constante cualquiera, y calculamos su
°ujo a trav¶es de una super¯cie esf¶erica centrada tambi¶en respecto al origen, como
la fuerza, de radio R tendremos que
Á =
Z
S
C
br
r2 ¢ d~S
y aqu¶³ considerando que para este caso la fuerza siempre corta perpendicularmen-te
a nuestra esfera, y la distancia a ella siempre es R tendremos, extrayendo las
constantes y realizando el producto escalar
Á =
C
R2
Z
S
dS

que, simplemente, dar¶a Á = C
R2 4¼R2 y, por tanto
Á = 4¼C:
Esta ley encontrada para un caso muy particular, se puede demostrar no obs-tante,
que sirve tambi¶en tomando un campo gravitatorio o electrost¶atico cualquiera
y una super¯cie cerrada cualquiera. Por tanto, cualquiera que sea la super¯cie que
tomemos
Á = 4¼Kq; (10.1)
donde q es la carga encerrada por la super¯cie, para el caso electrost¶atico, o bien
Á = ¡4¼Gm; (10.2)
siendo ahora m la masa total que encierra la super¯cie.
Este resultado, en cuya demostraci¶on general no vamos a entrar, resulta muy
importante y ¶util, ya que es pr¶actico para resolver bastantes problemas, y se conoce
con el nombre de Ley de Gauss para el campo electrost¶atico o gravitatorio, en
honor de su descubridor.
10.7. Circulaci¶on
± Se de¯ne la circulaci¶on de un campo vectorial ~M
a lo largo de un reco- Ampliaci¶on
rrido l como la integral a lo largo de la l¶³nea de la componente del campo que
es paralela a dicha l¶³nea.
Esta de¯nici¶on se puede expresar matem¶aticamente como
Z
L
~M
¢~l
:
Como podemos observar esta nueva magnitud, la circulaci¶on. no es m¶as
que la de¯nici¶on matem¶atica de una magnitud f¶³sica que ya conocemos: el
trabajo.
10.8. Representaci¶on gr¶a¯ca de los campos
10.8.1. Campo escalar
Representar un campo escalar se puede realizar por medio de sus super¯cies
de nivel, es decir, uniendo con una l¶³nea todos los puntos que presente el mismo
potencial, y observando estos dibujos tendremos una idea de c¶omo se comporta este
campo. Un ejemplo podr¶³an ser las l¶³neas de nivel de un mapa geogr¶a¯co. En ¶el
se indican cuanto vale en cada punto la altura. Basta echar una ojeada a un mapa
geogr¶a¯co para, observando d¶onde se acumulan m¶as l¶³neas de nivel saber que en
esos puntos la pendiente ser¶a mayor.
± Adem¶as, en este ejemplo, el campo escalar de las alturas coincide (salvo Ampliaci¶on
una constante) con el campo escalar potencial gravitatorio. De esta manera
un punto donde hay muchas l¶³neas de nivel supone un punto donde hay mu-cha
variaci¶on de energ¶³a potencial. La variaci¶on la proporciona la derivada del
escalar, en este caso el gradiente. Si esta derivada es alta el gradiente ser¶a con-siderable.
Pero el gradiente de un potencial con signo menos es la fuerza que
se siente en ese punto. C¶omo entender esto desde nuestro mapa geogr¶a¯co?,
es sencillo, all¶³ donde las curvas de nivel est¶an muy juntas el terreno es muy
empinado, tiene mucha pendiente, y la fuerza que se ejerce sobre nosotros
en esos puntos ser¶a muy pronunciada (hacia arriba o hacia abajo) porque el
gradiente lo es. O escrito de otra forma qui¶en no ha sentido la di¯cultad de

subir o bajar por un terreno muy escarpado?. Esta di¯cultad que nos propor-cionan
las fuerzas gravitatorias se puede ya ver gracias a la representaci¶on de
un mapa con l¶³neas de nivel.
10.8.2. Campo vectorial
Aunque representar un campo vectorial no es sencillo una manera de hacerlo
es mediante el concepto de las l¶³neas de fuerza, que son l¶³neas tangentes en todo
punto a la direcci¶on del campo. Si el campo fuera uno de velocidades estas l¶³neas
coincidir¶³an con las trayectorias de las part¶³culas sometidas a dicho campo. Algunas
propiedades de estas l¶³neas es que no pueden cortarse1 pues, si as¶³ fuera, tendr¶³amos
que en ese punto habr¶³a dos valores para el mismo campo. Para lograr que estas
l¶³neas nos hablen del m¶odulo del campo (es decir, de su intensidad) se dibujan de
tal manera que la densidad de l¶³neas sea proporcional a dicho m¶odulo.
Cuando un campo es conservativo, a los puntos donde las l¶³neas convergen, se
juntan, se denominan sumideros, y a aquellos de donde surgen o nacen fuentes.
As¶³ cualquier planeta es un sumidero de campo gravitatorio, y un prot¶on ser¶³a
una fuente de campo electrost¶atico.
1M¶as que en puntos singulares, sitios donde la fuerza es in¯nito. . .

Cap¶³tulo 11
Gravitaci¶on y campo
gravitatorio
La ley de Newton ~F = m~a es muy ¶util para indagar c¶omo se mueve un cuerpo
sometido a una cierta fuerza, pero no obstante hay algunas situaciones en las cuales
hay que indagar cual es la fuerza a la que se ve sometido un cuerpo determinado.
Entre estas fuerzas las m¶as conocidas son la gravitatoria y la electrost¶atica, de
aspecto muy similar pero or¶³genes distintos.
No obstante estas fuerzas aparecen gracias a una extra~na acci¶on a distancia.
Para evitar este concepto se introduce el concepto de campo, como una deforma-ci
¶on que sufre el espacio1 que posibilita esta acci¶on a distancia entre unas part¶³culas
y otras.
11.2. Ley de la gravitaci¶on universal
11.2.1. Enunciado
Esta ley, descubierta por Newton, a¯rma que dos masas cualesquiera experimen-tan
una atracci¶on entre ellas en la l¶³nea que une sus cuerpos y que dicha atracci¶on
es proporcional a sus masas e inversamente proporcional al cuadrado de la distancia
que las separa, es decir
~F = ¡G
Mm
r2 br (11.1)
En esta ley si tomamos j~rj =
p
x2 + y2 podemos decir tambi¶en que
Fx = ¡GMm x
r3
Fy = ¡GMm y
r3
¾
Donde M es la masa de un cuerpo, m la del otro, r el m¶odulo de la distancia
que hay entre ellos, que podemos expresar como r =
¡
x2 + y2 + z2
¢ 1
2 y G es la
constante de gravitaci¶on universal cuyo valor experimental es aproximadamente
G = 6;672 ¢ 10¡11m3kg¡1s¡2:
1O el espacio-tiempo.
65

CAP¶ITULO 11. GRAVITACI ¶ON Y CAMPO GRAVITATORIO
11.2.2. Las leyes de Kepler
Estas leyes de ¶³ndole emp¶³rica son
1. Los planetas describen ¶orbitas el¶³pticas y planas alrededor de su sol, donde
¶este ¶ultimo ocupa el foco de la elipse.
2. El vector de posici¶on con respecto al sol de un planeta cualquiera barre ¶areas
iguales en tiempos iguales.
3. Los planetas que giran alrededor de una misma estrella cumplen que T 2 / R3,
siendo T su periodo y R la distancia a la estrella.
11.2.3. Principio de superposici¶on
La ley descubierta por Newton se aplica al hallar la fuerza de atracci¶on entre
dos ¶unicos cuerpos puntuales. Por eso es l¶ogico preguntarse que suceder¶a cuando
tenemos tres o m¶as cuerpos que se atraen gravitatoriamente entre s¶³. Para ello se
ha descubierto el principio de superposici¶on.
Este principio indica simplemente que, a la hora de calcular cual ser¶a la fuerza
que siente una part¶³cula por otro conjunto de part¶³culas, basta sumar vectorialmente
las fuerzas.
Esta propiedad, pese a que estamos acostumbrados a ella, no deja de ser sorpren-dente.
De alguna forma la perturbaci¶on que se crea en el espacio y que logra que los
cuerpos se atraigan, es independiente de si ya existe otra perturbaci¶on creada por
el mismo cuerpo, y simplemente se suman sus resultados respectivos para formar el
total.
Ampliacio¶n ± Esta propiedad general que presenta la f¶³sica en muchos campos se suele
llamar linealidad. Tambi¶en a veces se habla de f¶³sica lineal, ¶optica lineal, etc...
indicando aquellos ¶ambitos en los que es v¶alido a¯rmar que la perturbaci¶on
total es simplemente la suma de las perturbaciones parciales.
Recuerda . Para un conjunto de part¶³culas la fuerza gravitatoria que experi-menta
una part¶³cula es, simplemente, la suma de los vectores de cada
una de las fuerzas involucradas.
11.3. Campo gravitatorio
11.3.1. Concepto
Podemos decir que cuando un planeta gira alrededor del Sol es debido a que el Sol
tira de ¶el, a trav¶es de los millones de kil¶ometros de espacio vac¶³o e inerte, usando
para ello un concepto denominado acci¶on a distancia, es decir, esta misteriosa
capacidad de lograr que un cuerpo afecte a otro sin que haya nada en medio. No
obstante otra forma m¶as f¶³sica de interpretar el mismo suceso es suponer que el Sol
crea alg¶un tipo de perturbaci¶on, crea una entidad que hace que, cuando un planeta
se sit¶ua en el mismo espacio, ¶este se sienta atra¶³do. A esta perturbaci¶on es a la que
denomina campo.
Ampliacio¶n ± Pero por qu¶e a¯rmar que es ma¶s f¶³sico suponer la existencia de este
campo?. Para ello valg¶amonos de un ejemplo sencillo. Si en un estanque en
el cual hay bastantes olas porque un ni~no se est¶a ba~nando enfrente, nosotros
dejamos caer un corcho de una botella observaremos que ¶este oscila. La in-terpretaci
¶on de acci¶on a distancia postular¶³a que es el ni~no el que, de una
forma quiz¶as misteriosa ha logrado hacer oscilar el corcho. La interpretaci¶on
de campo sostiene que el ni~no crea una perturbaci¶on en el medio, en este caso

el agua, que se transmite y llega hasta el corcho, haci¶endole oscilar. Incluso
podr¶³amos ver que, como las ondas son esf¶ericas y se van haciendo cada vez
m¶as grandes, si su energ¶³a permanece constante, como ha de repartirse entre
la longitud de la onda total, que es 2¼r, su efecto decrecer¶a con el inverso de
la distancia. Podr¶³amos postular as¶³ la ley de acci¶on a distancia del ni~no sobre
los corchos de botella como todo ni~no en un estanque genera una fuerza os-cilatoria
sobre los corchos de los alrededores que depende directamente de la
fuerza del ni~no e inversamente de la distancia a dicho ni~no, pero no obstante
es mucho m¶as natural pensar que el ni~no se limita a realizar una perturbaci¶on
que afecta tarde o temprano al corcho.
Estas dos formas de ver el mismo fen¶omeno, no obstante, dejan claras dos
diferencias extraordinariamente importantes:
1. En la acci¶on a distancia no parece haber ning¶un inconveniente pa-ra
que dicha acci¶on se ejerza instant¶aneamente, pero en cambio cuan-do
usamos el concepto de campo parece l¶ogico que la perturbaci¶on se
propague y tarde, por consiguiente, cierto tiempo en alcanzar su obje-tivo.
Vemos pues que existe as¶³ una forma mucho m¶as tangible de ver
si el Sol genera un campo o una acci¶on a distancia. La respuesta es un
campo, aunque tendr¶³amos que irnos hasta la mec¶anica relativista, que
escapa de los objetivos de este libro, para comentar que, efectivamente,
la gravedad tarda en llegar desde el Sol hasta nuestro planeta cierto
tiempo. Concretamente, si logr¶asemos quitar repentinamente el Sol de
nuestro Universo la Tierra no se enterar¶³a de su ausencia gravitatoria
hasta pasado un cierto tiempo. A qu¶e velocidad se propaga esta altera-ci
¶on gravitatoria? A la velocidad de la luz c, como casi todo en mec¶anica
relativista.
2. La presencia de un campo implica de alguna forma la existencia de un
medio que propague la perturbaci¶on. Este medio ser¶³a el agua, en el
ejemplo did¶actico expuesto anteriormente, y el vac¶³o en nuestro caso con-creto
de la gravedad (y el electromagnetismo). Por tanto el vac¶³o no
est¶a tan vac¶³o como parece, sino que debe presentar una cierta estruc-tura
que permita transmitir estas alteraciones. A esta estructura Albert
Einstein, Minkowsky y otros la denominaron espacio-tiempo.
11.3.2. Entidad matem¶atica
Partiendo de la ecuaci¶on (11.1) de Newton para la gravitaci¶on podemos ver que,
si consideramos un cuerpo aislado, podemos suponer que este ejerce un campo igual
a la fuerza que experimentar¶³a una part¶³cula de masa m dividido, precisamente,
por esta masa m. As¶³ tenemos que el campo gravitatorio, que llamaremos ~g es,
simplemente
~g =
~ f
m
:
. El campo gravitatorio ~g que existe en cualquier sitio del espacio es Recuerda
igual a la fuerza neta que experimentar¶³a una part¶³cula de masa m en
dicho punto dividida por esa misma masa.
De esta manera, de forma general, tendremos que el campo ~g que genera una
part¶³cula de masa m ser¶a
~g = ¡
Gm
r2 br:
11.4. Energ¶³a potencial gravitatoria
Resulta muy interesante hacer un estudio sobre la energ¶³a potencial que puede
tener un cuerpo por el hecho de estar sumergido en un campo gravitatorio. Sabe-

mos ya que los campos gravitatorios producidos por una part¶³cula puntual, ser¶an
centrales y que toda fuerza central es conservativa y, por tanto, tendr¶a una energ¶³a
potencial. Ahora bien, saber cu¶al ser¶a ¶esta puede ser o no sencillo. Veremos en este
caso cu¶al es dicha energ¶³a potencial gravitatoria.
La energ¶³a potencial es f¶acilmente obtenible a trav¶es del trabajo que supone
desplazar una part¶³cula o cuerpo desde una posici¶on hasta otra. Esto es as¶³ porque
esta magnitud nos expresa una cierta energ¶³a especial, ya que la tiene el cuerpo
por ocupar una posici¶on, y la energ¶³a est¶a ¶³ntimamente relacionada con el trabajo.
As¶³ podemos plantear cu¶al ser¶a dicho trabajo como
WAB =
Z B
A
~F(~r) ¢ d~l
:
Como dicho trabajo resulta venir de una fuerza conservativa central emplearemos
la misma t¶ecnica que se usaba para ver que las fuerzas centrales eran conservativas:
separamos mentalmente la trayectoria en ¶orbitas perpendiculares a la fuerza, en
las cuales el trabajo ser¶a cero, y otras paralelas a dicha fuerza. En las fuerzas
centrales las ¶orbitas perpendiculares en todo punto a la fuerza resultan ser c¶³rculos
conc¶entricos. As¶³ pues s¶olo va a intervenir el trabajo realizado por alejar o acercar
un cuerpo del origen, y la ecuaci¶on anterior pasar¶a a ser
WAB =
Z rB
rA
F(r)dr;
en donde s¶olo intervienen los m¶odulos. Basta ahora recordar que F = ¡GMm
r2 para
obtener que
WAB = ¡
Z rB
rA
GMm
r2 dr = GMm
µ
1
rB ¡
1
rA
¶
:
Como WAB = Ep( ~ rA) ¡ Ep( ~ rB) tenemos por ¯n que:
Egrav
p (~r) = ¡
GMm
r
: (11.2)
Nota ¦
1. Intentando interpretar el resultado (11.2) tenemos que para que la energ¶³a
potencial gravitatoria de un cuerpo sea cero ¶este debe encontrarse en el
in¯nito!. C¶omo se entiende esto?. Como el alcance de la fuerza gravi-tatoria
es in¯nito el hecho de que un cuerpo deje de sentirla supone que
dicho cuerpo est¶a in¯nitamente alejado. ¶Ese es, en principio el signi¯cado
de esta elecci¶on de origen de energ¶³a potencial.
2. Otro dato signi¯cativo es el hecho de que dicha energ¶³a sea negativa.
Hasta ahora todas las energ¶³as nos hab¶³an salido positivas. Qu¶e puede
signi¯car que una energ¶³a sea negativa?. Para ello vamos a pensar en lo
que supone tener un cuerpo con energ¶³a cero. Te¶oricamente ¶este ser¶³a un
cuerpo incapaz de producir trabajo alguno. No es dif¶³cil asociar este cuer-po
con uno situado en el vac¶³o m¶as absoluto, aislado y quieto en nuestro
sistema de referencia. Como no tiene velocidad ni hay perturbaci¶on al-guna
su energ¶³a deber¶³a ser cero. Pensemos ahora en que hay que hacer
para que un cuerpo parado en las cercan¶³as de otro llegue a tener energ¶³a
cero. Para ello deber¶³amos aislarle del otro, y para hacerlo le alejamos
hasta el 1. Ahora bien, como el otro cuerpo le atrae hemos de aportar
energ¶³a para alejarle hasta dejarle aislado. Ahora bien, si para que este
cuerpo tenga una energ¶³a nula hemos de darle nosotros energ¶³a, signi¯ca
que, de alguna forma, este cuerpo debe energ¶³a, pues hemos de d¶arsela
nosotros para que su energ¶³a total sea cero. Precisamente como debe
energ¶³a tenemos que su Ep es menor que cero.

11.5. Problemas concretos
11.5.1. C¶alculo de la fuerza gravitatoria ejercida por un sis-tema
de part¶³culas
Recordando el principio de superposici¶on enunciado en 11.2.3, para calcular la
fuerza que sobre una part¶³cula de masa m y radio ~r ejerce un sistema de i part¶³culas
con masas mi; i = 1; :::;N y radios ~ri basta sumar todos los campos producidos,
esto es
~F =
XN
i=1
~Fi = ¡
XN
i=1
Gmmi
(~r ¡~ri)2 (rd¡ ri)
11.5.2. C¶alculo de la fuerza gravitatoria ejercida por un cuer-po
continuo
Si debemos calcular la fuerza gravitatoria que ejerce un cuerpo continuo debere-mos,
aplicando el principio enunciado en 11.2.3, sumar todas las contribuciones.
Para una suma continua hemos de recurrir al c¶alculo integrar y lograr as¶³ conseguir
~F = ¡
Z
Gm
(~r0 ¡~r)2 (r0d¡ r)dm:
Despu¶es como se hace usualmente se reemplaza dm por ½(~r)dV y se integra.
¦ Esta integraci¶on, que en el caso general puede resultar complicada, queda Nota
muy simpli¯cada en problemas que presenten simetr¶³a eligiendo adecuadamen-te
el sistema de coordenadas.
11.5.3. Problemas de sat¶elites
Para resolver problemas de sat¶elites generalmente basta con lograr relacionar su
velocidad con la altura a la que ¶orbita. Para ello se supone que describen una ¶orbita
circular a velocidad angular constante y que, por tanto, debe existir una fuerza que
proporcione la aceleraci¶on normal necesaria. Esta fuerza es la gravitatoria.
Sabiendo entonces que
m
v2
R
=
GMm
R2
y relacionando v con otras magnitudes como v = R! y ! = 2¼
T suele bastar para
sacar estos problemas.
11.5.4. Velocidad de escape
Se llama velocidad de escape a aquella que hay que dar a un cuerpo para que
logre desligarse de la atracci¶on gravitatoria a la que se encuentra sometido. Como
desligar a un cuerpo de la atracci¶on gravitatoria supone en cierta medida aislarlo del
cuerpo que lo atrae, necesitaremos que la energ¶³a que tenga dicho cuerpo, sea, por
lo menos, nula. En caso contrario tendr¶a una cierta energ¶³a potencial negativa, que
supondr¶a que a¶un se encuentra ligado con el sistema que le atrae. As¶³ pues tomando
que la energ¶³a total, suma de cin¶etica y potencial debe ser cero, tendremos que
1
2
mv2 ¡
GMm
r
= 0
y de aqu¶³ se puede extraer dicha conclusi¶on. Se ha aplicado la ecuaci¶on (11.2).
Es notable que la resoluci¶on de este problema supone el claro entendimiento de la
secci¶on 11.4.

dm
D
x
L
Figura 11.1: Campo ~g generado por una varilla delgada.
11.5.5. Medida de la gravedad en la super¯cie de un planeta
El valor de ~g en la super¯cie de un planeta ser¶a sencillamente el valor que el
campo ~g tiene en dicho punto y, por tanto
~g =
GM
R2
donde M es la masa del planeta y R el radio que dicho planeta tiene.
11.5.6. C¶alculo de la atracci¶on gravitatoria de algunos s¶olidos
simples
Para algunos s¶olidos simples o que presenten simetr¶³a se puede calcular con
relativa sencillez la atracci¶on gravitatoria que ejercen, o su campo ~g. Generalmente
bastar¶a integrar en unos casos y aplicar astutamente el teorema de Gauss en otros.
Varilla delgada horizontal
Para lograr calcular cual puede ser el campo que se ejerce a una distancia D de
una varilla delgada, como la de la ¯gura 11.1 tomemos un punto cualquiera a una
distancia x. La peque~na masa dm generar¶a un campo d~g que ser¶a
d~g = ¡G
dm
x2 ^{:
En estos casos siempre se toma la varilla homog¶enea, de donde dm = ¸dx, aunque
si no lo fuera tendr¶³amos que dm = ¸(x)dx y se integra entre los extremos que hay
masa, es decir, x variando entre D y D + L. As¶³ tenemos que
~g =
Z
d~g =
Z L+D
D ¡G
¸
x2 dx^{ =
GM
L
µ
1
D ¡
1
L + D
¶
^{
donde hemos sustituido ¸ = M
L .
Plano in¯nito
Si tenemos un plano in¯nito y queremos hallar el campo en cualquier punto
tendremos que, necesariamente, en dicho punto el campo tiene que ser perpendicular
al plano. Esto es as¶³ porque al ser el plano in¯nito en cualquier zona que estemos
estamos en el medio del plano, es decir, hay la misma cantidad de masa en todas
las direcciones. Podemos usar el teorema de Gauss para resolver este problema.
Tomando como super¯cie un cilindro perpendicular al plano y de tal manera que
la mitad este a un lado y la otra mitad al otro tendremos que el °ujo total que
atraviesa ser¶a Á = ¡4¼GM donde M = ¾S siendo ¾ la densidad super¯cial y S
el ¶area que encierra el cilindro, que ser¶a la misma que la de su tapa. EL °ujo se
puede calcular f¶acilmente. Ser¶a solamente el de las tapas, pues los bordes resultan

paralelos al campo que, como hemos dicho antes, es perpendicular. En las tapas,
por simetr¶³a, el campo ser¶a el mismo a lo largo de toda la tapa, y como adem¶as
ser¶a perpendicular a ella tendremos que el °ujo total resulta ser Á = ¡2Sg donde el
2 es debido a que tiene dos tapas, y ¡Sg es sencillamente el campo por la super¯cie
que, en este caso particular y sencillo, nos dar¶a el °ujo.
Relacionando ahora con la ecuaci¶on de Gauss anteriormente escrita tenemos que
¡4¼G¾S = ¡2Sg y de esta manera deducimos que g = 2¼G¾ que, de forma un
tanto sorprendente, no depende de la distancia a la que estemos del plano.
¦ Como ejercicio puede ser interesante plantearse el campo gravitatorio Nota
que generar¶³a un hilo recto homog¶eneo in¯nitamente largo.
Campo gravitatorio de un objeto esf¶erico homog¶eneo2
Si tenemos un objeto esf¶erico homog¶eneo podemos decir, por simetr¶³a, que el
campo que genere ser¶a central. Entonces tomaremos como super¯cie de Gauss una
esfera m¶as grande que el objeto, conc¶entrica con ¶el y cuyo radio, tomando como
origen el centro del objeto, sea r. Dado que el campo de la esfera es central ¶este
cortar¶a perpendicularmente a la super¯cie de Gauss en todo punto, de donde el °ujo
ser¶a sencillamente Á = ¡g4¼r2 pues g es el m¶odulo del campo, a¶un no sabemos
cuanto, y 4¼r2 la super¯cie total de la esfera que usamos como super¯cie de Gauss.
Igualando este resultado con (10.2) tendremos que
¡4g¼r2 = ¡4¼Gm
y, por tanto, el resultado es que la esfera act¶ua como si toda su masa estuviera
concentrada en su centro, pues
g =
Gm
r2 :
2Al menos a capas.

Cap¶³tulo 12
Campo y potencial el¶ectrico
12.1. Preliminar
Las leyes de este tema y las formas de resoluci¶on de problemas son muy similares
en forma y contenidos a las del tema anterior. Por esta raz¶on se ver¶an un poco m¶as
escuetamente sus leyes. De todas formas hay que tener en cuenta que esta analog¶³a
se produce entre dos magnitudes tan diferentes como la atracci¶on gravitatoria y la
el¶ectrica, cuya diferencia en ¶ordenes de magnitud es del orden de 1020.
12.2. Ley de Coulomb
Dos cargas el¶ectricas puntuales se atraen (o repelen) entre s¶³ con una fuerza
dada por
~F =
1
4¼²0
qQ
r2 ^r (12.1)
Q y q son los valores de las cargas involucradas, que deber¶an llevar su corres-pondiente
signo, ²0 se denomina permitividad del vac¶³o. A veces al valor 1
4¼²0
se le
denota con la letra K y su valor aproximado es de 9;00 ¢ 109Nm2=C2.
12.2.1. Principio de superposici¶on
La fuerza que ejercen un sistema de cargas sobre otra es igual a la suma (vecto-rial)
de las fuerzas de cada una de las cargas del sistema sobre la otra. Quiere decir
esto que dado un sistema de cargas puntuales de posiciones ~ri y cargas qi, la fuerza
que ejercen sobre otra carga q situada en ~r ser¶a
~F =
XN
i=1
1
4¼²0
qiq
j~ri ¡~rj2
rid¡ r:
12.3. Campo el¶ectrico
Es la fuerza por unidad de carga que experimentar¶a una carga en cierta posici¶on
del espacio. Obedece a la f¶ormula
~E
=
~F
q
:
Debido tambi¶en al principio de superposici¶on, la expresi¶on del campo el¶ectrico en
una posici¶on ~r del espacio creado por un sistema de N cargas de valor qi; i = 1; : : :N
73

CAP¶ITULO 12. CAMPO Y POTENCIAL EL¶ECTRICO
y posici¶on ~ri ser¶a
~E
=
XN
i=1
1
4¼²0
qi
j~ri ¡~rj2
rid¡ r:
En el caso de tener un sistema continuo esta f¶ormula anterior quedar¶a transfor-mada
en
~E
=
Z
V
1
4¼²0
½(~r0)
j~r0 ¡~rj2
r0d¡ r dV:
Recuerda . La fuerza y el campo el¶ectrico son magnitudes vectoriales que cum-plen
el principio de superposici¶on. Por tanto se podr¶an sumar como
vectores.
12.4. Ley de Gauss
Recordando que el °ujo es la cantidad de campo vectorial que pasa por unidad
de super¯cie, tendremos que, para el campo el¶ectrico ~E
el °ujo ser¶a
ÁE =
Z
S
~E
¢ d~S
:
Siguiendo un razonamiento similar al que se puede realizar para el caso gravita-torio,
la ley de Gauss nos dice que
ÁE = 4¼KQ =
Q
²0
:
Nota ¦ En este caso, como las cargas pueden ser tanto positivas como negativas,
puede resultar que, pese a que existan cargas en el interior de la super¯cie su
carga neta sea nula (se anulen unas con otras) y el °ujo sea cero.
La ley de Gauss resulta muy ¶util para la resoluci¶on de problemas con simetr¶³a
plana, cil¶³ndrica o esf¶erica.
12.5. Potencial y energ¶³a el¶ectrica
Potencial es la circulaci¶on del campo el¶ectrico entre dos puntos A y B, es decir
V (~rA) ¡ V (~rB) =
Z B
A
~E
(~r) ¢ d~l
: (12.2)
Si en esta f¶ormula multiplicamos ambos miembros por q, como ~F = q~E
tendre-mos
que el trabajo el¶ectrico realizado para desplazar una carga q desde una posici¶on
A hasta otra B ser¶a simplemente WA!B = q(V (A) ¡ V (B)).
An¶alogamente la energ¶³a el¶ectrica, es decir, la energ¶³a potencial el¶ectrica que
tendr¶a una carga por encontrarse inmersa en un campo el¶ectrico, ser¶a tal que
WA!B = Ep(~rA) ¡ Ep(~rB) = q(V (A) ¡ V (B)). Esto supone que
Ee
p(~r) = qV (~r):
Recuerda . Tanto la energ¶³a como el potencial y el trabajo son magnitudes
escalares y por tanto se expresar¶an como un n¶umero normal (con sus
correspondientes unidades, eso s¶³). Adem¶as, en virtud del principio de
superposici¶on el potencial el¶ectrico de un conjunto de part¶³culas es la
suma del creado por cada uno de ellas. Como el potencial es escalar
ser¶a tan f¶acil como sumar sus magnitudes.

+
+
+
+
-
-
-
-
+
+
+
+
-
-
-
-
+
+
+
-
-
-
+
+
-
-
V1 V2 V
Figura 12.1: Asociaci¶on de condensadores en serie y en paralelo.
12.5.1. Algunos casos particulares de potencial el¶ectrico
Carga puntual
Usando la ecuaci¶on (12.2) con el valor de ~E
para una carga puntual, que es
~E
= 1
4¼²0
q
r2 ^r e integrando, se llega f¶acilmente a la conclusi¶on de que
V (r) =
1
4¼²0
q
r
:
Campo el¶ectrico constante
Un sencillo uso de (12.2) nos lleva directamente a la expresi¶on
V (x) = ¡Ex;
donde suponemos que el campo ~E
es constante, y as¶³ el potencial depende de una
cierta cantidad unidimensional x. Un buen ejemplo ser¶³a el campo creado por un
plano cargado in¯nito. En este caso x ser¶³a la distancia al plano.
12.6. Condensadores
Un condensador es un dispositivo capaz de almacenar carga el¶ectrica. B¶asica-mente
est¶an formados por dos conductores situados uno frente al otro, lo m¶as cerca
posible, dejando entre medias de ellos un aislante que puede ser el vac¶³o o un
diel¶ectrico.
Existe una relaci¶on de proporci¶on entre el potencial creado entre los dos polos¢ de un condensador y la carga almacenada. Matem¶aticamente se puede expresar de
una manera simple como
Q = CV;
donde C es la constante de proporcionalidad, denominada capacidad. La unidad de
la capacidad es el faradio.
¦ Un faradio es una unidad muy grande. (Al estilo del culombio). Por ello Nota
lo com¶un es encontrarse con microfaradios, nanofaradios o picofaradios.
12.6.1. Asociaci¶on de condensadores
Serie
En dos condensadores situados en serie, como en el primer gr¶a¯co de la ¯gura
12.1 la diferencia de potencial total que cae entre el primero y el segundo ser¶a la

suma de las diferencias parciales de cada condensador, es decir, ¢VT = ¢V1 +¢V2.
No obstante, al encontrarse unidos en serie la carga de ambos deber¶a ser igual1, y
adem¶as ser¶a la carga total almacenada por la asociaci¶on. As¶³ tenemos que Q1 =
Q2 = QT y podemos poner
¢Vt = ¢V1 + ¢V2 =
Q
C1
+
Q
C2
y de aqu¶³ se deduce f¶acilmente que la capacidad efectiva de la asociaci¶on es
1
C
=
1
C1
+
1
C2
:
Paralelo
Si situamos dos condensadores asoci¶andolos en paralelo, como se puede ver en
el segundo dibujo de la ¯gura 12.1, tendremos que la diferencia de potencial entre
ambos deber¶a ser igual, y adem¶as ser¶a la diferencia de potencial total. Esto es
as¶³ porque tenemos unidos los dos polos de los condensadores por un conductor,
y por tanto la ca¶³da de potencial entre los polos opuestos tiene que ser la misma.
A su vez, como cada condensador almacenar¶a una carga distinta, tendremos que
para la asociaci¶on total
QT = Q1 + Q2 = C1¢V + C2¢V = (C1 + C2)¢V:
Se ve pues, de manera sencilla, que la capacidad efectiva o equivalente de dos con-densadores
asociados en paralelo obedece a la ley
C = C1 + C2:
1Pues si no se producir¶³a un desplazamiento de cargas.

Cap¶³tulo 13
Movimiento arm¶onico simple
Hay muchas situaciones en f¶³sica en las cuales la fuerza que siente una part¶³cula
en cierto sistema es proporcional a un desplazamiento respecto cierto punto de
equilibrio. Es decir, existen sistemas para los cuales es v¶alida la ley de Hooke
F = ¡kx (13.1)
o al menos, lo es manteniendo el m¶ovil entre ciertos l¶³mites. Estos sistemas se dice
de ellos que describen un movimiento arm¶onico simple.
La intenci¶on de este apartado es estudiar este tipo de movimientos, dada su
importancia y su sencillez.
¦ En todo el estudio que se haga en este cap¶³tulo se tratar¶a el problema Nota
de manera unidimensional.
± Se puede demostrar que la gran mayor¶³a de los sistemas que tiene un
punto de equilibrio estable admiten un tratamiento armo¶nico para pequen~as Ampliacio¶n
oscilaciones en torno a dicho punto. Esto se puede ver desarrollando en serie de
Taylor alrededor del punto y d¶andose cuenta de que como la primera derivada
ser¶a nula el primer t¶ermino que aparecer¶a ser¶a, precisamente, el t¶ermino de
un potencial arm¶onico: k
2 x2.
13.2. Din¶amica del sistema
13.2.1. Ecuaci¶on del movimiento
Si aplicamos la ley de Newton, F = ma junto con la ley de Hooke, obtendremos
que
ma = ¡Kx ) ma + Kx = 0:
Esta sencilla ecuaci¶on es, no obstante, algo m¶as complicada de resolver que otras
anteriores, puesto que las magnitudes involucradas, a y x dependen La una de la
otra, concretamente como a = dx
dt2
dx
dt2 +
K
m
x = 0
que constituye una ecuaci¶on diferencial, ya que involucra derivadas de funciones con
la propias funciones. Resolver esta ecuaci¶on est¶a bastante m¶as all¶a del ¶ambito de este
curso, pero a¶un as¶³ es f¶acil darse cuenta de que las funciones sin y cos van a tener
77

CAP¶ITULO 13. MOVIMIENTO ARM¶ONICO SIMPLE
algo que ver, dado que son las ¶unicas que al ser derivadas dos veces y sumadas
consigo mismas dan nulo. Manipulando algunos coe¯cientes en estas funciones y
operando se encuentra la soluci¶on m¶as general a este movimiento, que es
x = Asin(!t + Á) (13.2)
y que por tanto constituye la ecuaci¶on de movimiento de un sistema que cumpla
la ley de Hooke, o bien de un movimiento arm¶onico simple.
Signi¯cado de la ecuaci¶on
En esta ecuaci¶on A es la amplitud m¶axima que puede recorrer el m¶ovil, ! es
la frecuencia angular de la oscilaci¶on, es decir, el n¶umero de radianes que da en
un segundo. Como parece que la palabra radi¶an no tiene sentido para un muelle,
por ejemplo, quiz¶as sea preferible pensar en la frecuencia del movimiento f = !
2¼
es decir, el n¶umero de oscilaciones completas que da en un segundo, o bien tomar
T = 2¼
! el periodo de la oscilaci¶on, que ser¶a el tiempo que tarda nuestro sistema en
dar una oscilaci¶on completa.
Por ¶ultimo qu¶e ser¶a Á?. Notemos que, si tomamos t = 0 tendremos que en el
instante 0, el cuerpo que realiza un movimiento estaba en la posici¶on x = sin(Á),
por lo que Á, par¶ametro al que se conoce con el nombre de fase, nos indica cuando
empieza el movimiento.
13.2.2. Periodicidad de la ecuaci¶on
Fij¶andose en la ecuaci¶on (13.2) se puede observar que, la existencia de una
funci¶on seno para describir este movimiento, nos va a llevar irremediablemente hacia
un movimiento de tipo peri¶odico. Efectivamente, si tuvi¶eramos un resorte perfecto,
este estar¶³a oscilando eternamente describiendo el mismo movimiento en cada
oscilaci¶on.
Para adivinar cada cuanto se repite el movimiento bastar¶a igualar el argumento
del seno a 2¼, pues como se sabe sin(2¼ + Á) = sin(Á). De esta manera tendremos
que el movimiento se repetir¶a, esto es, har¶a un periodo, cuando !t = 2¼, lo cual
supone que el periodo T ser¶a, como ya hab¶³amos dicho, T = 2¼
! .
Es tambi¶en frecuente describir el movimiento arm¶onico simple como la analog¶³a
de una proyecci¶on sobre el eje OY o bien OX de un movimiento circular de velocidad
angular constante !.
13.2.3. Velocidad
Para hallar la velocidad que un m¶ovil sometido a una fuerza arm¶onica presenta
en un instante t basta derivar su ecuaci¶on del movimiento. As¶³ tendremos que, como
v = dx
dt
v = A! cos(!t + Á);
relacion ¶que nos ofrece la velocidad de un movimiento armonico ¶para cualquier
instante. Es tambi¶en p
comun ¶relacionar la velocidad con la posicion, ¶cosa sencilla
notando que cos =
1 ¡ sin2 y que, por tanto
q
A! cos(!t + Á) = A!
1 ¡ sin2(!t + Á)
de donde, introduciendo la amplitud A en la ra¶³z cuadrada
v = !
q
A2 ¡ A2 sin2(!t + Á)

y ahora, echando un vistazo a la relaci¶on (13.2) se ve que
v = !
p
A2 ¡ x2;
siendo esta la relaci¶on entre v y x buscada.
13.2.4. Aceleraci¶on
La aceleraci¶on a la que se encuentra sometido un m¶ovil que describe un movi-miento
arm¶onico simple se puede obtener teniendo presente (13.2) y que a = dx
dt2 .
Por tanto
a = ¡A!2 sin(!t + Á):
Si queremos obtener una relaci¶on de la aceleraci¶on con respecto a la posici¶on del
m¶ovil podemos recurrir a observar la similitud entre la ecuaci¶on anterior y la que
describe la ecuaci¶on de movimiento de un m.a.s., o bien utilizando las leyes de
Newton y Hooke poner que
F = ma = ¡Kx ) a = ¡
K
m
x:
13.3. Energ¶³a
13.3.1. Energ¶³a cin¶etica
Partiendo de la relaci¶on de la energ¶³a cin¶etica de un m¶ovil, y de la ecuaci¶on de
velocidad del m.a.s. se tiene que
Ec =
1
2
K cos2(!t + Á);
o, relacion¶andolo con la posici¶on
Ec =
1
2
K(A2 ¡ x2):
13.3.2. Energ¶³a potencial
Es conservativo el movimiento arm¶onico simple? Podemos de¯nir un potencial
para ¶el?. La respuesta es s¶³, por tratarse de una fuerza central1. En este caso cu¶al
ser¶a el potencial?. Para hallarlo recordamos que
WA!B = Ep(A) ¡ Ep(B) =
Z B
A
F dx;
y que, por tanto, tendremos que
Ep(A) ¡ Ep(B) =
Z B
A ¡Kx dx = ¡
1
2
Kx2
¸B
A
= ¡
1
2
KB2 +
1
2
KA2;
siendo ahora ya muy sencillo identi¯car la energ¶³a potencial en una posici¶on x como
Ep(x) =
1
2
Kx2:
1Aunque estemos haciendo un estudio unidimensional, no por ello dejamos de tener una fuerza
central.

13.3.3. Energ¶³a mec¶anica
Para obtener la energ¶³a mec¶anica o total puesta en juego en un movimiento
arm¶onico simple sumaremos las energ¶³as potencial y cin¶etica respecto a la posici¶on.
As¶³ tendremos que
ET =
1
2
K(A2 ¡ x2) +
1
2
Kx2 =
1
2
A2:
Nota ¦ En el movimiento armo¶nico simple se ve, de una forma que casi roza
en lo magistral, lo que la conservaci¶on de la energ¶³a supone en f¶³sica. En
este caso toda la energ¶³a est¶a dada por la f¶ormula 1
2A2, que es la energ¶³a
potencial m¶axima que alcanza el muelle por separarle una distancia A de
su posici¶on de equilibrio. M¶as tarde, cuando empieza el movimiento, ¶este va
adquiriendo energ¶³a cin¶etica, siempre a costa de su energ¶³a potencial, y por
tanto acerc¶andose a la posici¶on de equilibrio. Cuando el m¶ovil se encuentra en
la posici¶on de equilibrio su energ¶³a potencial es nula, pero el cuerpo conserva
una cantidad de energ¶³a cin¶etica que se ir¶a ahora utilizando en comprimir
otra vez el muelle hasta su amplitud m¶axima, y que contribuir¶a, por tanto,
a incrementar nuevamente la energ¶³a potencial. En cualquier caso la suma de
ambas nos dar¶a la energ¶³a m¶axima puesta en juego, que se conserva.
Ampliacio¶n ± En un muelle real la conservacio¶n de la energ¶³a no se cumple, ya que
siempre existen p¶erdidas por rozamiento. Estas p¶erdidas dan lugar a lo que se
denomina un movimiento arm¶onico simple amortiguado, ya que la amplitud va
disminuyendo poco a poco, inform¶andonos a su vez de la cantidad de energ¶³a
que se est¶a perdiendo.
Una forma de solucionar este fen¶omeno es aportando algo de energ¶³a extra
al m¶ovil, para contrarrestar la que pierde por rozamiento. Esto puede dar lugar
a resonancias y otros fen¶omenos f¶³sicos muy interesantes.
13.4. El p¶endulo simple
Hay ciertos sistemas que, si bien no son estrictamente sistemas sometidos a una
fuerza tipo Hooke, si pueden, bajo ciertas condiciones, considerarse como tales. El
p¶endulo simple, es decir, el movimiento de un grave atado a una cuerda y sometido
a un campo gravitatorio constante, es uno de ellos.
Al colocar un peso de un hilo colgado e inextensible y desplazar ligeramente el
hilo se produce una oscilaci¶on peri¶odica. Para estudiar esta oscilaci¶on es necesario
proyectar las fuerzas que se ejercen sobre el peso en todo momento, y ver que
componentes nos interesan y cuales no. Esto se puede observar en la ¯gura 13.1.
Vemos pues que, considerando ¶unicamente el desplazamiento tangente a la tra-yectoria,
es decir, el arco que se est¶a recorriendo, podemos poner
ml
d2®
dt2 + mg sin(®) = 0 (13.3)
donde no hemos hecho sino aplicar la segunda ley de Newton. Esto se puede ver
considerando que el arco es l® y, como l es la longitud del hilo y es constante2,
la aceleraci¶on ser¶a l d2®
dt2 . Por otra parte, aplicando
P ~F = m~a, en este caso la
fuerza es s¶olo la de la gravedad, mg que se descompone en una componente, que se
contrarresta con la tensi¶on, m¶as otra, que es la que hace que exista movimiento en
la trayectoria marcada por el arco.
Esta ecuaci¶on diferencial no es nada f¶acil de resolver3 y por ello recurrimos a
la aproximaci¶on siguiente: suponiendo que el ¶angulo que desplazamos es peque~no,
2Se considera un hilo inextensible.
3Realmente no tiene soluci¶on anal¶³tica.

mg
Tensión (T)
-T
a
a
mg sen a
l
Figura 13.1: Descomposici¶on de las fuerzas en un p¶endulo.
tomamos que sin(®) ' ® y as¶³ tenemos que
d2®
dt2 +
g
l
® = 0 (13.4)
que a veces tambi¶en se expresa como Ä® + g
l ® = 0.
Esta ecuaci¶on es absolutamente an¶aloga a la de un movimiento arm¶onico simple,
y por tanto su soluci¶on tambi¶en ser¶a (13.2) teniendo, ¶unicamente, la precauci¶on de
sustituir el valor de ! antiguo por el que tiene ahora para un p¶endulo
! =
r
g
l
:
A partir de aqu¶³ se pueden extraer todas las dem¶as relaciones para un p¶endulo
simple, el periodo, frecuencia, etc.

Cap¶³tulo 14
Ondas
Existen en la naturaleza muchos fen¶omenos de los cuales se dice tienen natu-raleza
ondulatoria pero qu¶e es exactamente una onda? Qu¶e propiedades tienen?
C¶omo se puede formalizar una expresi¶on matem¶atica de un fen¶omeno ondulatorio?.
Estas y otras cuestiones son el tema objeto de este cap¶³tulo.
No obstante, antes de entrar de lleno en lo que es una onda y su formalismo,
vamos a de¯nir onda como:
. Una onda es una perturbaci¶on f¶³sica que transmite energ¶³a y mo- Recuerda
mento lineal, pero que no transmite materia.
En las ondas materiales las part¶³culas concretas que componen el material no se
propagan, sino que se limitan a oscilar alrededor de su posici¶on de equilibrio. No
obstante cuando una onda se transmite por dicho material se produce una sincro-nizaci
¶on de oscilaciones entre las distintas part¶³culas componentes del medio que
posibilita la propagaci¶on de un momento lineal y una energ¶³a.
± Matem¶aticamente todas las ondas deben satisfacer la ecuaci¶on de ondas, Ampliaci¶on
que es
@2f(x; t)
@x2 =
1
v2
@2f(x; t)
@t2 ;
siendo v la velocidad de propagaci¶on de la onda en el medio. Se podr¶³a demos-trar
(aunque no es trivial) que algunas velocidades de propagaci¶on de ondas
son v =
q
T
½l
para una onda que viaja por una cuerda de densidad lineal ½l y
tensi¶on T as¶³ como v =
q
E
½
1 para una onda sonora que circula por un medio
cuyo m¶odulo de Young sea E y densidad sea ½.
14.1.1. Tipos de ondas
Podemos establecer criterios de clasi¯caci¶on de las ondas. Algunos ser¶³an:
Seg¶un el medio por el que se propaguen.
² Ondas que requieren medio material para propagarse. Ejemplo, el sonido.
² Ondas que no requieren un medio material. Ejemplo, la luz.
Seg¶un el n¶umero de dimensiones que involucran.
1Se trata, por tanto, de una ecuaci¶on para hallar la velocidad del sonido en un medio.
83

CAP¶ITULO 14. ONDAS
² Unidimensionales. Ejemplo, la propagaci¶on del movimiento en una cuer-da.
² Bidimensionales. Ejemplo, olas en la super¯cie de un l¶³quido.
² Tridimensionales. Ejemplo, el sonido normal.
Seg¶un la relaci¶on entre la vibraci¶on y la direcci¶on de propagaci¶on.
² Transversales. Son aquellas ondas en las cuales la oscilaci¶on es perpen-dicular
a la direcci¶on de propagaci¶on de la onda. Por ejemplo en una
cuerda normal y tensa la onda se propaga de izquierda a derecha (en
cierto caso particular) pero, en cambio, la oscilaci¶on de un punto concre-to
de la cuerda se produce de arriba a abajo, es decir, perpendicularmente
a la propagaci¶on.
² Longitudinales. En este tipo la propagaci¶on es paralela a la oscilaci¶on.
Como ejemplo, si apretamos un muelle las espiras oscilan de izquierda a
derecha y de derecha a izquierda, paralelas en cualquier caso a la direcci¶on
de propagaci¶on.
14.2. Ecuaci¶on general de una onda
Supongamos que, en una cuerda tensa, creamos una forma f en determinado
instante y despu¶es observamos como se propaga a una velocidad v. Esto supone que
la deformaci¶on que antes hab¶³a parat = 0 en x = 0 deber¶a desplazarse de tal forma
que, siendo coherente con su velocidad, se encuentre en x = vt en un tiempo t. Esto
se puede lograr considerando la funci¶on de onda
f(x; t) = f
³
t ¡
x
v
´
(14.1)
que nos ofrece una ecuaci¶on de onda que se desplaza de izquierda a derecha. Si qui-si
¶eramos obtener una onda desplaz¶andose de derecha a izquierda bastar¶³a sustituir
el signo por uno positivo y tener
f(x; t) = f
³
t +
x
v
´
:
14.3. Ecuaci¶on de una onda arm¶onica
La ecuaci¶on considerada en (14.1), si bien es correcta, no obstante es de una
generalidad tan amplia que su estudio no es sencillo y no aportar¶³a tampoco datos
muy signi¯cativos. Es por eso conveniente particularizar al caso de ondas arm¶onicas,
tomando la funci¶on f(t) como f(t) = Asin(!t) tendremos que
Ã(x; t) = Asin
³
!
³
t ¡
x
v
´´
:
Esta ecuaci¶on presenta una doble periodicidad temporal y espacial que ser¶a muy
¶util estudiar. No obstante antes de hacer un estudio m¶as formal es conveniente
plantearse intuitivamente qu¶e est¶a sucediendo en esta onda. Como la funci¶on sin(x)
es una funci¶on peri¶odica que contiene in¯nitos bucles signi¯ca que, si dejamos
el tiempo ¯jo y nos vamos desplazando por el eje OX desde cierto punto, tarde
o temprano encontraremos otro punto desde el cual se ve la misma forma de la
onda. La distancia entre estos dos puntos se llama longitud de onda ¸ y por ver la
misma forma de la onda nos referimos a observar ondas en la misma fase, es decir,
si en el primer punto vemos el seno en un m¶aximo, por ejemplo, buscaremos en el

segundo punto otra vez el seno en un m¶aximo, o si en el primer punto est¶a el seno
en un cero, pero subiendo, buscaremos el segundo punto en la misma situaci¶on: un
cero subiendo. . .
Otra periodicidad que encontramos se nota al tomar la distancia ¯ja e ir variando
el tiempo. Dado un cierto instante t0 veremos que en un punto ¯jo x0 va variando
la posici¶on hasta que, al cabo de un tiempo t0 + T x0 se encuentra igual que en t0.
A esta cantidad T se la denomina periodo.
¦ Quiz¶as se pregunte el lector que utilidad puede tener tomar una funci¶on Nota
tan particular como la funci¶on sin(x) para hacer nuestro desarrollo de las
ondas. Esta elecci¶on por una raz¶on: Matem¶aticamente el teorema de Fourier
demuestra que toda funci¶on f(x) puede ponerse como una suma de funciones
sin(x) y cos(x) y siempre es m¶as sencillo operar con estas funciones que con
la funci¶on general f(x).
14.3.1. Periodo y frecuencia
Calculemos expl¶³citamente cuanto es T. Tenemos una onda particularizada en
un tiempo t0 y una posici¶on x0, nos dar¶a un desplazamiento en el eje y concreto
que ser¶a
y(t0;x0)(x0; t0) = Asin
³
!
³
t0 ¡
x0
v
´´
:
Al cabo de un cierto tiempo T, cuando el cron¶ometro marque t0 +T debemos tener
la misma situaci¶on, es decir, y(t0+T;x0) = y(t0;x0), por tanto
Asin
³
!
³
t0 ¡
x0
v
´´
= Asin
³
!
³
t0 + T ¡
x0
v
´´
:
Esta situaci¶on se produce para las funciones seno y coseno cuando su argumento
aumenta en una cantidad 2¼, con lo cual tenemos que:
!
³
t0 ¡
x0
v
´
+ 2¼ = !
³
t0 + T ¡
x0
v
´
y de esta expresi¶on es sencillo deducir la siguiente, e interesante relaci¶on
T =
2¼
!
. Por tanto el periodo est¶a relacionado con la frecuencia angular ! mediante esta
relaci¶on, que es la misma que para un movimiento arm¶onico simple. An¶alogamente
podemos de¯nir la frecuencia f o º como el inverso del periodo, es decir
º =
1
T
=
!
2¼
:
En la ¯gura 14.1 se ha representado lo que supone el transcurrir del tiempo para
una onda arm¶onica y como ¶esta se repite al cabo de un tiempo T.
14.3.2. Longitud de onda y n¶umero de ondas
Procedamos de manera similar al apartado 14.3.1 pero ¯jando ahora el tiempo
y dejando que la coordenada x var¶³e desde x0 hasta x0 + ¸. Tendremos entonces
que
!
³
t0 ¡
x0
v
´
+ 2¼ = !
µ
t0 ¡
x0 + ¸
v
¶
y esto supondr¶a la relaci¶on:
!¸
v
= 2¼

tiempo
t=0
En un periodo T la onda se repite.
t=T
Figura 14.1: Periodo de una onda arm¶onica.

0
Elongacion (x)
tiempo(t)
l
l
A
Figura 14.2: Longitud de onda de una onda arm¶onica.
que cuando se pone en funci¶on de T adquiere el singular aspecto de
v =
¸
T
;
es decir, la velocidad de propagaci¶on es el espacio que recorre la propagaci¶on en
un cierto tiempo dividido por ese tiempo. Tomando el tiempo como un periodo
obtenemos que la longitud que recorre es ¸ y el tiempo que tarda es T.
Se suele de¯nir tambi¶en n¶umero de ondas como
k =
2¼
¸
:
Poniendo as¶³ la funci¶on de onda arm¶onica en funci¶on de ! y k queda la sencilla
expresi¶on.
Ã(x; t) = y(x; t) = Asin(!t ¡ kx):
En la ¯gura 14.2 se puede ver de manera gr¶a¯ca lo que representa la magnitud ¸.
14.4. Consideraciones energ¶eticas de las ondas
14.4.1. Energ¶³a
Para llegar a la expresi¶on de la energ¶³a que propaga una onda vamos a tomar
como caso particular el de una onda propag¶andose por una cuerda tensa. En este
caso la energ¶³a total involucrada por cada part¶³cula i es la que corresponder¶³a a un
movimiento arm¶onico simple, que puesto en funci¶on de la masa y de ! ser¶a
Ei =
1
2
miA2!2
siendo mi la masa correspondiente a la part¶³cula i. La energ¶³a total ser¶a la suma a
toda la cuerda de las energ¶³as de cada part¶³cula i. Hay que tener en cuenta que la

amplitud A y la velocidad angular ! van a ser constantes en toda la cuerda, y por
tanto
E =
X
i
Ei =
X
i
1
2
miA2!2 =
1
2
A2!2
X
i
mi:
La suma a la Masa de cada part¶³cula ser¶a la masa total de la cuerda, que podemos
poner en funci¶on de su densidad lineal como mtotal = ½ll. Con esto nos queda que
E =
1
2
A2!2½ll: (14.2)
14.4.2. Potencia
Cu¶al ser¶a la potencial transmitida?. Para ello basta tener presente que P = E
t
y, dividiendo as¶³ la expresi¶on (14.2) por t y considerando que la longitud recorrida
en la cuerda por unidad de tiempo va a coincidir con la velocidad de propagaci¶on,
tendremos que
P =
1
2
A2!2½lv (14.3)
14.4.3. Intensidad
Se de¯ne la magnitud intensidad de una onda como la potencia por unidad de
¶area que atraviesa una super¯cie. Para el caso de una onda plana la intensidad es
igual a
I =
1
2
A2!2½v:

Cap¶³tulo 15
Fen¶omenos ondulatorios
Los procesos en los cuales intervienen ondas dan lugar a una serie de fen¶omenos
especiales, dada la naturaleza particular de las ondas, que son de interesante estudio,
y que explican muchas de las asombrosas propiedades que tiene tanto la luz como
el sonido. En el caso de la luz podemos explicar en qu¶e consisten los fen¶omenos de
re°exi¶on y refracci¶on y qu¶e leyes gobiernan estos fen¶omenos. Tambi¶en habr¶a que
dedicar un apartado al fen¶omeno f¶³sico que se produce cuando se superponen dos o
m¶as ondas: la interferencia, y por ¶ultimo, tratar algunos temas someramente para un
conocimiento cualitativo por parte del lector, como son los temas sobre la difracci¶on
y la polarizaci¶on de las ondas.
15.2. Principio de Huygens
El principio de Huygens es una herramienta ¶util y bastante sencilla para en-tender
muchos de los extra~nos procesos que suceden relacionados con las ondas. Si
bien no es estrictamente correcto y adem¶as se acepta sin una demostraci¶on riguro-sa,
sirve para explicar satisfactoriamente algunos fen¶omenos ondulatorios como la
interferencia, re°exi¶on (¯gura 15.6) o refracci¶on (¯gura 15.8).
B¶asicamente este principio explica c¶omo tiene lugar la propagaci¶on de una onda:
cuando cada uno de los puntos de un medio material es alcanzado por una onda,
este punto se vuelve a comportar como un foco emisor de ondas, creando una serie
de ondas secundarias. El resultado global de todos estos puntos emitiendo ondas a
la vez ser¶a la de un nuevo frente de ondas similar al anterior, con lo que la onda se
ir¶a propagando sucesivamente.
15.3. Interferencia entre ondas
Qu¶e suceder¶a cuando dos ondas se cruzan?. Esta es la pregunta que queremos
explicar en este apartado. Para resolverla hemos de volver a recurrir a nuestro co-nocido
el principio de superposici¶on, es decir, que podemos considerar el resultado
¯nal como una mera suma de los efectos causados por la primera onda m¶as la se-gunda.
Recordemos que este principio parece ser una propiedad de la naturaleza,
ya que el efecto de aplicar dos ondas consecutivas sobre un mismo medio no tendr¶³a
por que dar como resultado la simple suma de ambas ondas.
. Al propagarse dos o m¶as ondas por un medio la perturbaci¶on to- Recuerda
89

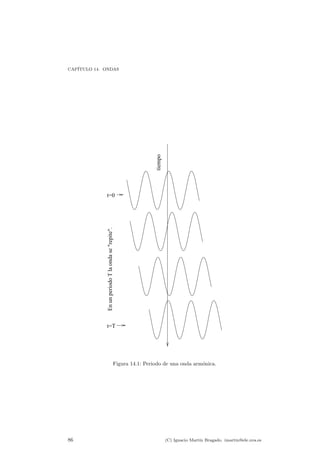
CAP¶ITULO 15. FEN¶OMENOS ONDULATORIOS
d
d
2
1
d - d 2 1
Figura 15.1: Esquema de un fen¶omeno de interferencias.
tal resultante es, simplemente, la suma de las perturbaciones de ambas
ondas.
Vamos a utilizar el principio de superposici¶on para estudiar algunos casos sen-cillos
de interferencia entre ondas.
15.3.1. Ondas coherentes: Interferencias constructivas y des-tructivas
Supongamos que tenemos dos ondas tales que su longitud de onda, frecuencia
y amplitud son iguales, y que sus fases o bien son iguales, o bien presenta una
cierta discrepancia que permanece constante. Son precisamente este tipo de ondas
las que reciben el nombre de ondas coherentes. Matem¶aticamente llamemos Ã a una
onda y Á a la otra y supongamos que queremos calcular el efecto que hacen sobre
un cierto punto. Ahora bien, los puntos de aplicaci¶on del foco de dichas ondas no
tienen por que coincidir, por lo que las distancias a dicho punto ser¶an distintas, y
las llamaremos d1 y d2. Tomaremos su frecuencia como ! y su longitud de onda
¸ aunque, no obstante, vamos a realizar el tratamiento matem¶atico expresando
las ondas en funci¶on del n¶umero de ondas k para simpli¯car un poco la notaci¶on.
As¶³ pues tendremos que una onda ser¶a
Ã = Asin(!t ¡ kd1)
y la otra
Á = Asin(!t ¡ kd2):
La onda resultante ser¶a la suma de ambas, es decir
ª = Ã + Á: (15.1)
Hagamos ahora un poco de ¶algebra, la expresi¶on (15.1) una vez sustituida se
transforma en
ª = Asin(!t ¡ kd1) + Asin(!t ¡ kd2)

2
1.5
1
0.5
0
-0.5
-1
-1.5
-2
sin(x)
sin(x+.1)
sin(x)+sin(x+.1)
-10 -5 0 5 10
Figura 15.2: Representaci¶on de una interferencia (casi) constructiva.
que al extraer factor com¶un a la amplitud da como resultado
ª = A(sin(!t ¡ kd1) + sin(!t ¡ kd2)):
Apliquemos ahora la igualdad trigonom¶etrica siguiente
sin(A) + sin(B) = 2 sin
µ
A + B
2
¶
cos
µ
A ¡ B
2
¶
(15.2)
a nuestra expresi¶on de ª y el resultado ¯nal ser¶a que
ª = 2Asin
µ
!t ¡ k
d1 + d2
2
¶
cos
µ
kd2 ¡ kd1
2
¶
: (15.3)
Interpretar este resultado es sencillo, pero no por ello poco sorprendente. Si
hacemos la sustituci¶on d = d1+d2
2 tendremos que la onda resultante es una onda
que parece provenir de una distancia d, que es la semisuma de las distancias a
ambos focos, pero cuya amplitud no es constante, sino que depende del t¶ermino
2Acos
¡ kd2¡kd1
2
¢
y que por tanto va a variar seg¶un el punto del plano y las relaciones
entre las distancias a los focos, como se representa en la ¯gura 15.1.
Interferencia constructiva
Concretamente esta amplitud ser¶a m¶axima en los lugares en los cuales cos
¡ kd2¡kd1
2
¢
=
1 y m¶³nima para aquello sitios donde cos
¡ kd2¡kd1
2
¢
= 0. Analizando esto un poco
m¶as profundamente tendremos que aquellos puntos que veri¯quen
kd2 ¡ kd1
2
= n¼
tendr¶an una amplitud m¶axima. En ellos se producir¶a lo que se denomina interferen-cia
constructiva, ya que en dichos puntos las ondas se funden constructivamente
dando lugar a una amplitud que es la suma de ambas amplitudes. Un ejemplo se ve
representado en la ¯gura 15.2, donde la interferencia no es puramente constructiva,
porque si no se ver¶³a ¶unicamente el dibujo de una onda, pero s¶³ existe un desfase
tan peque~no como para ver qu¶e signi¯ca este tipo de interferencia.

1
0.8
0.6
0.4
0.2
0
-0.2
-0.4
-0.6
-0.8
-1
sin(x)
sin(x+3.14)
sin(x)+sin(x+3.14)
-10 -5 0 5 10
Figura 15.3: Representaci¶on de una interferencia destructiva.
Interferencia destructiva
A su vez, en los sitios donde este coseno modulador sea nulo, que ser¶an aquellos
para los cuales se cumpla
kd2 ¡ kd1
2
= (2n + 1)
¼
2
tendremos que la amplitud ser¶a siempre cero, independientemente del tiempo que
pase, ya que al ser cero uno de los dos t¶erminos de la ecuaci¶on (15.3) el resultado total
ser¶a nulo y no depender¶a del tiempo. Entonces a estos puntos que nunca presentan
amplitud se les denomina nodos y a las l¶³neas que los unen se las denomina l¶³neas
nodales. Un ejemplo de interferencia destructiva est¶a representado en la ¯gura 15.3.
N¶otese que el resultado de la suma de las ondas es una l¶³nea plana, una onda de
amplitud nula.
Recuerda . Interferencia constructiva supone amplitud ma¶xima, destructiva
implica amplitud nula.
Nota ¦ Se puede intentar entender estos resultados utilizando un poco de in-tuici
¶on f¶³sica. Una interferencia constructiva se producir¶a cuando la diferencia
de fase sea de n¼ pero dicha diferencia est¶a marcada por el t¶ermino
kd2 ¡ kd1
2
que, puesto en funci¶on de ¸ resulta ser
¼
³
d2
¸
¡
d1
¸
´
:
Igualando esta diferencia de fase a n¼ tendremos que
d2 ¡ d1 = n¸
lo cual constituye una f¶ormula mucho mas inteligible que las anteriores. Re-sulta
que para puntos separados una longitud entera de longitudes de onda la


a

d
1
d
D
y
a
a
d2 - d 1
2
Figura 15.4: Experiencia de Young.
interferencia es constructiva. Un c¶alculo similar para interferencia destructiva
nos llevar¶³a a que
d2 ¡ d1 =
³
n +
1
2
´
¸:
Qu¶e signi¯ca esto?. Pues sencillamente que si la distancia entre los puntos
es un n¶umero entero de longitudes de onda, como ambas ondas parten con la
misma fase de sus focos respectivos, cuando llegan se encuentran una frente
a la otra variadas en lo que han logrado recorrer de m¶as o de menos en esta
diferencia de distancias. Si esta diferencia es de un n¶umero entero de lamb-das
ambas ondas se encuentran exactamente igual, porque la funci¶on seno es
peri¶odica y se repita cuando ha avanzado espacialmente esta magnitud ¸. En
cambio si ha avanzado cierto n¶umero de lambdas m¶as la mitad de una ¸ re-sulta
que las ondas se encuentran en contra-fase, o bien que una es justo la
opuesta de la otra1 y por tanto ambas se anulan simult¶aneamente.
Experiencia de Young
± Consiste esta experiencia en hacer iluminar dos rendijas muy peque~nas Ampliaci¶on
y separadas una distancia a, tambi¶en peque~na, con un foco de luz. A una
distancia d medida desde la mitad de las rendijas, y que debe ser mucho
mayor que a, se puede observar que existir¶a un m¶aximo, una interferencia
constructiva, si
ay
d
= n¸;
siendo y la distancia vertical medida desde el centro de la pantalla de obser-vaci
¶on, como se ha representado en la ¯gura 15.4.
Ser¶³a un ejercicio interesante para el lector intentar demostrar esto par-tiendo
de la relaci¶on para un m¶aximo d2 ¡ d1 = n¸ y la ¯gura 15.4.
15.3.2. Ondas estacionarias: Propagaci¶on en direcciones o-puestas
Vamos ahora a proponer una forma un poco diferente de interferencia. Tome-mos
como ejemplo una cuerda y ¯j¶emosla por uno de sus extremos. (En un gancho
de una pared, por ejemplo). Si propagamos ahora una onda por la cuerda esta tarde
1Ya que sin(® + ¼) = ¡sin(®).

o temprano llegar¶a a la pared y rebotar¶a en ella. Tendremos entonces una interfe-rencia
que se producir¶a en la cuerda, debida a dos ondas iguales, con la excepci¶on de
que se propagan en sentido contrario. Se va a adelantar ya que este tipo de situaci¶on
se denomina ondas estacionarias.
Matem¶aticamente lo que tenemos es que una onda presenta la forma
Á = Asin(!t ¡ kx)
y la otra, por propagarse en sentido contrario, ser¶a
Ã = ¡Asin(!t + kx)
, donde el signo negativo es debido a que al rebotar tambi¶en se produce un cambio
de fase de ¼ radianes, siendo la resultante la suma de ambas, por tanto
© = Á + Ã = Asin(!t ¡ kx) ¡ Asin(!t + kx):
Para ver que signi¯ca esta expresi¶on se va a volver a utilizar la relaci¶on (15.2) de la
suma de dos funciones seno, nos dar¶a
© = 2Acos(!t) sin(kx): (15.4)
Qu¶e signi¯ca (15.4)?. Tenemos que destacar algunos puntos:
No se trata de una onda propiamente dicha, pues no aparece un t¶ermino que
contenga una dependencia espacial y temporal, sino que estas dependencias
aparecen separadas.
La energ¶³a no se puede propagar por la cuerda. Esto es debido a que aquellos
puntos para los cuales sin(kx) = 0 van a estar siempre quietos, ya que no
presenta ninguna otra dependencia. Evidentemente la energ¶³a no podr¶a reba-sar
estos puntos para propagarse al otro lado. Por tanto esta construcci¶on no
es una onda normal, no es una onda viajera; precisamente por esto se la
denomina onda estacionaria.
Un punto cualquiera de la cuerda se limitar¶a a moverse de forma arm¶onica en
el tiempo, debido al t¶ermino cos(!t) con una amplitud 2Asin(kx).
A los puntos que cumplen sin(kx) = 0 y que por tanto, van a estar siempre
quietos, se les denomina nodos. En nuestro caso tendremos nodos en las posiciones
en las cuales kx = n¼.
Onda estacionaria en una cuerda ¯ja por ambos extremos
Este es un caso interesante y con ciertas aplicaciones pr¶acticas. Como ejemplo,
en cualquier instrumento de cuerda tendremos una disposici¶on de este tipo.
Vamos a hacer un an¶alisis semi-cuantitativo de este fen¶omeno. Si en este caso
la cuerda debe estar sujeta por ambos extremos signi¯ca que dichos extremos no
van a poder moverse. Deber¶an ser por tanto nodos. Esto nos lleva a a¯rmar que
sin(k0) = 0 y sin(kL) = 0 donde se ha supuesto, como resulta l¶ogico, que la cuerda
empieza en x = 0 y acaba en x = L. La primera condici¶on es trivial y es siempre
cierta, pero la segunda nos ofrece que
kL = n¼
expresi¶on que hay que interpretar. Es ¶esta una relaci¶on entre el n¶umero de ondas
k y la longitud de la cuerda L. Ahora bien, puesto que la longitud L de la cuerda
es algo que podemos variar a nuestro antojo lo que tenemos realmente es que el

n¶umero de ondas no puede ser uno cualquiera, sino que debe cumplir que k = n¼
L ,
es decir ser discreto y con unos valores concretos2. Poniendo estos valores en funci¶on
de ¸ tenemos que
¸ = 2
L
n
;
y como tambi¶en existe una relaci¶on entre ¸ y T y T = º¡1 podemos por ¯n expresar
la frecuencia de la vibraci¶on como
º = n
v
2L
donde v es la velocidad de propagaci¶on de la onda (si se propagara).
Este resultado s¶³ que es extraordinariamente interesante, porque nos dice que
la frecuencia de la onda va a estar delimitada por el valor de su longitud L. A¶un
as¶³ para una longitud L tendremos una serie de frecuencias diferentes seg¶un el valor
de n que tomemos, que se denominan arm¶onicos. Esta es la raz¶on fundamental
de la existencia de los instrumentos de cuerda, como por ejemplo una guitarra.
Como la frecuencia de la oscilaci¶on se propaga por el aire y se escucha como sonido,
tendremos que podemos variar la nota bien cambiando la longitud de la cuerda L,
por ejemplo, poniendo el dedo sobre un traste y acortando esta longitud en cierta
cantidad determinada, o bien variando la velocidad de propagaci¶on de la onda en la
cuerda, que depend¶³a de la tensi¶on y la densidad: es decir, bien a¯nando la guitarra,
es decir, aumentando y disminuyendo la tensi¶on de la cuerda, o bien variando la
densidad de la cuerda poniendo una primera en vez de una segunda, o una tercera,
etc. . .
15.4. Otras propiedades de las ondas
15.4.1. Difracci¶on
La difracci¶on es un fen¶omeno caracter¶³stico de las magnitudes ondulatorias, ca-racterizado
por la propagaci¶on an¶omala de dicha magnitud en las cercan¶³as de
un obst¶aculo o una abertura comparable, en tama~no, a su longitud de onda.
En un lenguaje m¶as intuitivo: la difracci¶on supone una contradicci¶on a nuestra
idea preconcebida de que la luz se propaga en l¶³nea recta, observ¶andose en las
cercan¶³as de esquinas de obst¶aculos, o en los bordes de la sombra de la luz tras
atravesar una rendija estrecha, que dicha luz parece torcer la esquina o desviarse
de su trayectoria recta.
La difracci¶on es el resultado de una compleja serie de interferencias de las mag-nitudes
ondulatorias consigo mismas. Si en la luz no se observa aparentemente este
fen¶omeno, raz¶on por la cual surge nuestra idea preconcebida de la propagaci¶on en
l¶³nea recta de la luz, es debido a que, como ya se ha dicho antes, este fen¶omeno
aparece s¶olo cuando el tama~no de los objetos o rendijas es comparable al de la
longitud de onda de la propagaci¶on. Como en el caso de la luz visible esta longitud
es diminuta. en nuestra experiencia macrosc¶opica y cotidiana de la existencia, no
tenemos consciencia de estos fen¶omenos.
15.4.2. Polarizaci¶on
En una onda transversal el movimiento de las part¶³culas que componen el medio
(o de los campos que oscilan, como en el caso de la luz), debe ser perpendicular a
la direcci¶on de propagaci¶on, Ahora bien, como la direcci¶on de propagaci¶on es una
recta en el espacio tridimensional, la perpendicular a esta recta supondr¶a un plano
2En lenguaje de f¶³sica moderna se podr¶³a decir que k est¶a cuantizado.

en el cual el medio puede desplazarse. Imaginemos que una onda se propaga en
el eje z. Esto supone que la oscilaci¶on deber¶a producirse ortogonal a dicho eje, es
decir, estar contenida en el plano xy. Pero no se nos dice si estando contenido en
dicho plano puede oscilar en sentido norte-sur, o este-oeste, o suroeste -nordeste,
etc. Esta libertad de elecci¶on que queda de la direcci¶on de vibraci¶on componente
de la onda se puede caracterizar en una propiedad que se denomina polarizaci¶on.
Polarizaci¶on de una onda ser¶a por tanto la direcci¶on concreta que toma dicha onda
en la vibraci¶on de sus part¶³culas componentes.
La luz normal, por ejemplo, no est¶a polarizada. Esto signi¯ca que var¶³a alea-toriamente
su direcci¶on de vibraci¶on en el plano perpendicular a la propagaci¶on.
Cuando esta variaci¶on no se produce, o bien se conoce con exactitud, se dice que la
onda est¶a polarizada, y adem¶as se puede de¯nir su tipo de polarizaci¶on.
Decir por ¶ultimo que existen dispositivos capaces de polarizar la luz, tales como
los polarizadores o polaroides.
15.4.3. Otras propiedades
Existen otras propiedades interesantes de los fen¶omenos ondulatorios en general
y la luz en particular, que quiero rese~nar aqu¶³, as¶³ como una serie de fen¶omenos
que son f¶aciles de explicar con las nociones que se recogen en p¶arrafos anteriores y
posteriores de este cap¶³tulo. Por ejemplo la dispersi¶on de la luz, responsable de que
el cielo sea azul y las puestas de sol rojizas, responsable tambi¶en de la salida del
arco iris cuando el sol logra iluminar el mundo en un d¶³a lluvioso. La re°exi¶on y
refracci¶on de la luz, que trataremos posteriormente, y causa de que podamos vernos
en un espejo, de los espejismos y de que las cucharillas se tuerzan cuando las
metemos en agua, causa tambi¶en de los halos que el sol y la luna ofrecen a veces.
As¶³ pues fen¶omenos como estos, o como el atractivo colorido que el aceite ofrece
sobre un charco, por qu¶e no vemos bien debajo del agua si abrimos los ojos al
l¶³quido elemento, o incluso por qu¶e los peces son plateados por su panza, pueden
explicarse utilizando algunos principios b¶asicos de interferencia de la luz en capas
delgadas, ¶³ndice de refracci¶on del agua frente al del cristalino e incluso re°exi¶on total
e ideas evolutivas darwinistas. Queda a juicio del lector estimar si la f¶³sica ofrece
s¶olo algunas explicaciones parciales e in¶utiles o si bien es capaz de formar parte
junto con la poes¶³a, la religi¶on y la m¶³stica de las doctrinas que son capaces de crear
una visi¶on global de la belleza de nuestro Universo, e incluso llegar a suplantarlas
alg¶un d¶³a. . .
15.5. Re°exi¶on y refracci¶on de la luz
Los fen¶omenos de re°exi¶on y refracci¶on se producen en general cuando un movi-miento
ondulatorio se encuentra en sus propagaci¶on con una super¯cie que separa
dos medios distintos. La parte de la onda que logra atravesar dicha super¯cie y pasar
al otro lado frecuentemente cambia de direcci¶on, conoci¶endose este fen¶omeno como
refracci¶on. Tambi¶en sucede que parte de la onda (o toda) rebota con la super¯cie,
denomin¶andose re°exi¶on a este fen¶omeno.
15.5.1. Re°exi¶on
La ley de la re°exi¶on se enuncia a¯rmando que, cuando un rayo de luz, o bien
la direcci¶on de propagaci¶on de un frente de ondas, se encuentra con una super¯cie,
la onda re°ejada lo har¶a con un ¶angulo igual que el de la onda incidente, medido
desde la perpendicular a la super¯cie donde se re°eja la onda.


q i q r

Figura 15.5: Re°exi¶on de una onda.

Ondas secundarias segun el principio de Huygens.
Figura 15.6: Explicaci¶on seg¶un el principio de Huygens de la re°exi¶on.
Tomando las magnitudes de la ¯gura 15.5 esto se expresa simplemente como
µi = µr.
15.5.2. Refracci¶on
La ley de refracci¶on nos ofrece el ¶angulo que adopta la propagaci¶on de la onda
en el segundo medio, medido tambi¶en respecto a la vertical a la super¯cie, como
se indica en la ¯gura 15.7. Adem¶as los rayos de incidencia, re°exi¶on y refracci¶on se
encuentran siempre en el mismo plano. La ley que relaciona el ¶angulo de incidencia
con el de refracci¶on se conoce como ley de Snell, que es
n1 sin µ1 = n2 sin µ2;
donde n1 y n2 son dos constantes relacionadas con las caracter¶³sticas de cada medio
y que se denominan ¶³ndice de refracci¶on. Este ¶³ndice de refracci¶on de un medio
resulta ser
n =
c
v
;
en donde v es la velocidad de la luz en dicho medio. Se deduce por tanto que para
luz en el vac¶³o cuya velocidad es c se tendr¶a que n = 1.
Re°exi¶on total
La ley de Snell es v¶alida para pasar de un medio a otro cualquiera. Cuando
tenemos que pasar de un medio 1 a otro 2 tal que n1 n2 tendremos que sin µ2 =
n1
sin µ1 y como n1
1 no habra ¶ningun ¶tipo de problema. Ahora bien, cuando
n2
n2
tengamos que n1 n2 entonces n1
n2
1 y al tomar sin µ2 = n1
n2
sin µ1 existir¶a un

q1
q2
Figura 15.7: Refracci¶on de una onda.
Medio 1.
Velocidad v
Ondas secundarias segun
el principio de
Huygens.
Medio 2.
Velocidad v
1
2
Figura 15.8: Explicaci¶on seg¶un el principio de Huygens de la refracci¶on.

¶angulo µl = arc cos n2
n1
tal que sin µ2 = 1. Qu¶e pasar¶a para ¶angulos µ1 µl?. Pues
suceder¶a que para estos sin µ2 1 y por tanto, nuestro problema no tendr¶a soluci¶on
real.
El signi¯cado f¶³sico de este fen¶omeno nos dice lo siguiente: en estos casos existe
una ¶angulo l¶³mite µl a partir del cual es imposible que se produzca el fen¶omeno de
refracci¶on y por tanto toda la luz que incida sobre esa super¯cie ser¶a re°ejada. Por
esta raz¶on a este fen¶omeno se le conoce como re°exi¶on total.
Un ejemplo pr¶actico se puede observar cuando se bucea: a partir de cierto ¶angulo
de inclinaci¶on en el cual miremos a la super¯cie del agua, veremos esta como un
espejo, pero no podremos ver absolutamente nada de lo que hay por encima del
agua.
15.5.3. Principio de Fermat
± Una forma muy elegante de entender estos fen¶omenos de re°exi¶on y Ampliaci¶on
refracci¶on, y que a¶un sigue siendo v¶alida, es hacer uso del principio de Fermat.
Dicho principio dice que la luz, para ir desde un punto A hasta otro B elige
siempre un camino tal que el tiempo en recorrerle sea el m¶³nimo (o, a veces el
m¶aximo). Es de notar que la ley a¯rma que es el tiempo el que es m¶³nimo, no
el espacio que recorre.
De esta forma en un mismo medio la luz viaja en l¶³nea recta, porque como
la velocidad es constante entonces el tiempo m¶³nimo lo logra con una distancia
m¶³nima, y ya se conoce que la recta es el camino m¶as corto entre dos puntos.
En cuanto a la re°exi¶on, resulta que si tenemos que ir de un punto A a
otro B pero tocando un espejo por el camino, la forma m¶as r¶apida en la cual
lo haremos ser¶a logrando que el ¶angulo de incidencia sea igual al de refracci¶on.
Por ¶ultimo para la refracci¶on: si debemos ir de un punto A en un medio
donde uno se desplaza muy r¶apidamente (por ejemplo) a otro punto B situado
en un medio distinto y donde la velocidad de desplazamiento resulta muy lenta,
nos resultar¶a m¶as favorable, para llegar antes, recorrer algo m¶as de espacio
donde la velocidad es m¶as r¶apida para poder as¶³ atajar algo de espacio en el
medio donde esta velocidad es lenta y recorrer all¶³ menos. Como ejemplo basta
pensar que a veces para ir de un sitio a otro preferimos tomar una autopista,
aunque demos un ligero rodeo, que una carretera de tierra y piedras que vaya
recta, sin poner en duda que aunque en la autopista recorremos m¶as camino
vamos a llegar antes.
Una explicaci¶on clara y amena de las leyes de refracci¶on y re°exi¶on gracias
al principio de Fermat puede ser consultada por el lector en el [1] cap¶³tulo 26.

Cap¶³tulo 16
Electromagnetismo
Si bien algunos efectos magn¶eticos han sido conocidos desde la antigÄuedad, como
por ejemplo el poder de atracci¶on que sobre el hierro ejerce la magnetita, no fue
sino hasta el siglo XIX cuando la relaci¶on entre la electricidad y el magnetismo
qued¶o patente, pasando ambos campos de ser diferenciados a formar el cuerpo de
lo que se conoce como electromagnetismo.
Con el advenimiento posterior de las ecuaciones de Maxwell, relaci¶on de ecuacio-nes
en las que quedan expresadas todas las leyes del electromagnetismo, qued¶o ce-rrado
el estudio cl¶asico de este campo. Tan importantes y logradas fueron estas
ecuaciones que Albert Einstein, eligiendo entre la veracidad de las ecuaciones de
Maxwell o la Mec¶anica Newtoniana, que no son compatibles entre si, logr¶o desban-car
la teor¶³a Newtoniana imponiendo la llamada Teor¶³a de la Relatividad.
En este nivel veremos algunas de las relaciones m¶as patentes entre la electricidad
y el magnetismo, as¶³ como las fuerzas a las que la aparici¶on de campos magn¶eticos
da lugar.
16.2. Fuerza de Lorentz
Dado un campo magn¶etico ~B
y una part¶³cula de carga q que se desplaza por el
interior de dicho campo con una velocidad ~v Lorentz descubri¶o que esta part¶³cula
sufre una fuerza magn¶etica igual a
~F = q~v ^ ~B
: (16.1)
Elementos a destacar de esta f¶ormula es que la fuerza magn¶etica se deja no-tar,
por tanto, s¶olo sobre part¶³culas cargadas; para part¶³culas neutras (q = 0) se
tendr¶a que ~F = 0. Un hecho a¶un m¶as rese~nable es que s¶olo act¶ua sobre part¶³cu-las
en movimiento. Si una part¶³cula est¶a en reposo respecto a nuestro sistema de
referencia la fuerza magn¶etica ejercida sobre ella, aunque est¶e cargada y exista un
campo magn¶etico, es nula.
¦ Para caracterizar el sentido del campo se puede emplear la denominada Nota
regla de la mano izquierda, consistente en que, si consideramos los dedos
pulgar, ¶³ndice y coraz¶on de la mano izquierda, de tal forma que el dedo coraz¶on
se~nale en la direcci¶on y sentido de la velocidad y el ¶³ndice en el del campo,
obtendremos el pulgar apuntando en la direcci¶on y sentido correctos de la
fuerza magn¶etica.
101

CAP¶ITULO 16. ELECTROMAGNETISMO
La unidad de campo magn¶etico en el Sistema Internacional es el Tesla. De la
ecuaci¶on (16.1) se puede extraer que dimensionalmente un Tesla ser¶a T = Ns
mC
Newton segundo entre metro Culombio.
Recuerda . La fuerza magn¶etica siempre es perpendicular a la trayectoria de
la part¶³cula y al campo magn¶etico
± Si, adem¶as de un campo magn¶etico existiera un campo el¶ectrico ~E
po-
Ampliaci¶on demos incluir esta fuerza en la Ley de Lorentz y, como la fuerza el¶ectrica es
simplemente ~F = q~E
y podemos usar el principio de superposici¶on
~F = q(~E
+~v ^ ~B
):
Un ejemplo de c¶omo se puede aplicar esta f¶ormula para campos magn¶eticos
constantes se puede ver en la secci¶on 16.5.1.
16.2.1. Fuerza sobre una corriente el¶ectrica
Pero. . . Y si en vez de una sola part¶³cula tenemos varias movi¶endose?, esto
es como preguntarse por la fuerza que experimentar¶a, debido al magnetismo, una
corriente el¶ectrica. Para ello vamos a suponer una corriente el¶ectrica y tomar un
elemento diferencial de ella. Si diferenciamos (16.1) tendremos que, como s¶olo la
carga q va a variar
d ~F = dq(~v ^ ~B
);
pero habr¶a que calcular cuanto puede ser este dq. Partiendo de la de¯nici¶on de
intensidad para una corriente el¶ectrica, I = dq
dt y sustituyendo dq tendremos que
d ~F = I dt~v ^ ~B
:
Veamos ahora que podemos hacer con esta expresi¶on usando la conocida f¶ormula
de la velocidad ~v = d~l
dt y sustituyendo por tanto d~l
= ~v dt:
d ~F = I d~l
^ ~B
:
Por ¶ultimo, recordando que en un circuito la intensidad, por la ley de Ohm,
depende s¶olo de la diferencia de potencial y la resistencia de dicho circuito y podemos
considerarla por tanto constante, tendremos que para un conductor ¯nito:
~F = I
Z
d~l
^ ~B
: (16.2)
16.3. Campo magn¶etico debido a una carga en mo-vimiento
La relaci¶on entre la electricidad y el magnetismo es tan ¶³ntima que cualquier
carga movi¶endose genera a su alrededor un campo magn¶etico. Deducir cual es dicho
campo a partir de principios iniciales no es f¶acil, y por eso se detalla aqu¶³ simple-mente
cual es el campo que genera una carga en movimiento:
~B
=
¹0
4¼
q
~v ^ br
r2 (16.3)
donde ¹0 es la constante correspondiente al campo magn¶etico, y se denomina per-meabilidad
magn¶etica del vac¶³o, q es la carga de la part¶³cula ~v es la velocidad a la
que se mueve y ~r es el vector que indica el lugar d¶onde queremos calcular el campo
pero visto desde un sistema de referencia centrado en la part¶³cula. Tambi¶en se la
conoce como ley de Biot y Savart.
Esta f¶ormula nos indica c¶omo el magnetismo est¶a creado por corrientes y no por
monopolos, es decir por cargas magn¶eticas del estilo de las cargas el¶ectricas.

¦ Como ejemplo para ver la naturaleza un poco distinta del campo mag- Nota
n¶etico basta considerar el intento de separar el polo de un im¶an. Aunque
rompamos un im¶an por la mitad este reproduce sus dos polos. Si ahora
partimos estos cachos otra vez en dos, nuevamente tendremos cada cachito con
dos polos norte y sur diferenciados. En magnetismo no existen los monopolos
± Una explicaci¶on detallada aunque con bastante nivel que deduzca m¶as Ampliaci¶on
rigurosamente estas expresiones y de razones para ellas puede buscarse en
cualquier libro que trate sobre electromagnetismo, ecuaciones de Maxwell o
incluso teor¶³a de la Relatividad.
16.3.1. Campo magn¶etico producido por una corriente el¶ec-trica
Si intentamos generalizar la f¶ormula (16.3) a una corriente el¶ectrica deberemos
pasar primero a una forma diferencial para intentar integrar despu¶es, igual que
hicimos con la fuerza de Lorentz. Para ello partimos de
d~B
=
¹0
4¼
dq
~v ^ br
r2
en donde, haciendo tambi¶en el cambio en funci¶on de la intensidad y teniendo en
cuenta que ~r es el punto donde queremos calcular el campo pero visto desde la carga,
si llamamos a ese punto ~r desde un sistema de coordenadas, y ~r0 a cada punto del
conductor que vamos a recorrer en la integraci¶on, tendremos que
~B
=
¹0
4¼
I
Z
d~l
^ rd¡ r0
(~r ¡~r0)2 :
16.4. Ley de Ampµere
El hecho de la no existencia de un monopolo magn¶etico va a hacer que en
cualquier situaci¶on entren y salgan l¶³neas de campo magn¶etico en cualquier vo-lumen
que queramos imaginar y que, por tanto, el °ujo del campo magn¶etico sea
nulo siempre, con lo cual no hay ningun ¶teorema similar al de Gauss para el campo
magn¶etico en cuanto R
a °ujo se re¯ere. Pero no obstante la circulacion ¶del campo
magn¶etico, es decir
~B
¢d~l
si que va a ser una magnitud interesante debido a que, se
puede demostrar, que la circulaci¶on del campo magn¶etico a trav¶es de una trayecto-ria
cerrada cualquiera va a ser igual a ¹0 por la intensidad de corriente que atraviesa
el plano encerrado por dicha super¯cie. Esta relaci¶on, expresada matem¶aticamente
se convierte en I
~B
¢ d~l
= ¹0I (16.4)
donde el s¶³mbolo
H
se utiliza para expresar integrales sobre trayectorias cerradas.
¦ El hecho de que la circulaci¶on del campo magn¶etico no sea nula para Nota
cualquier trayectoria indica que este campo no es conservativo, y por tanto no
vamos a lograr encontrar un potencial para ¶el. No obstante esto se re¯ere ¶uni-camente
al campo magn¶etico, no a la fuerza magn¶etica y no implica, por tanto,
la no conservaci¶on de la energ¶³a. Es m¶as, como la fuerza magn¶etica siempre es
perpendicular a la trayectoria esto supondr¶a que el trabajo magn¶etico siempre
es cero, es decir, no se produce trabajo magn¶etico.

16.5. Resoluci¶on de problemas t¶³picos
16.5.1. Part¶³cula sometida a un campo magn¶etico constante
y uniforme
Supongamos que tenemos una carga que entra en un campo magn¶etico con una
cierta velocidad y de tal forma que el campo magn¶etico sea perpendicular a dicha
velocidad. C¶omo se mover¶a en el seno de este campo?. Se puede entender de forma
intuitiva que al se ejercer¶a una fuerza sobre la carga que, debido a (16.1) debe ser
perpendicular a la velocidad con la que se desplaza la carga, y por tanto tendr¶a una
componente exclusivamente normal a la trayectoria. Como en todo momento la fuer-za
es perpendicular a la trayectoria, porque as¶³ lo exige la ley de Lorentz, tendremos
que la carga describir¶a una circunferencia, ya que estar¶a sometida a una fuerza que
crear¶a una aceleraci¶on normal constante y una aceleraci¶on tangencial nula. Podemos
por tanto igualar la fuerza centr¶³peta de este movimiento con la fuerza magn¶etica
y tener as¶³ que, si tomamos los m¶odulos,
qvB = m
v2
R
de donde se puede deducir que el radio de la trayectoria ser¶a
R =
mv
qB
:
16.5.2. Fuerza magn¶etica experimentada por un conductor
recto y perpendicular al campo magn¶etico
Podemos tomar un conductor recto y de longitud L que est¶a situado sobre el
eje OX. Un campo perpendicular a el puede ser ~B= B^|. Entonces utilizando la
expresi¶on (16.2) en donde d~l
= ^{dx tenemos que
~F = I
Z L
0
dx^{ ^ B^| = ILB^k
donde se ha supuesto que ~B
es constante.
16.5.3. Campo magn¶etico creado por un conductor recto e
in¯nito
Este problema es f¶acilmente resoluble utilizando la ley de Ampµere. Debido a la
simetr¶³a que va a presentar el problema podemos a¯rmar que el campo magn¶etico
ser¶a en cualquier punto perpendicular al hilo conductor (ya que ¶este es recto y en
el c¶alculo del campo ~B
aparece un producto vectorial) y, lo que resulta de gran
utilidad, su m¶odulo s¶olo puede depender de la distancia al hilo.
Aprovechando estas condiciones vamos a tomar como trayectoria una circunfe-rencia
centrada en el hilo conductor y perpendicular a ¶el. La circulaci¶on del campo
magn¶etico a trav¶es de este camino ser¶a
¹0I =
I
~B
¢ d~l
;
para hacer esta integral debemos darnos cuenta de que, en cualquier punto de la
trayectoria, ~B
va a resultar paralelo a d~l
y por tanto tendremos
¹0I =
I
B~dl

Idl
R
dBy
dBx
q
x
y
z
r
Figura 16.1: Geometr¶³a para calcular el campo magn¶etico en el eje de una espira.
y c¶omo adem¶as j~B
j va a resultar constante
¹0I = B
I
dl = B2¼r;
siendo r el radio de la circunferencia, que coincide con la distancia m¶³nima de un
punto cualquiera de nuestra trayectoria hasta al cable conductor. De esta ¶ultima
expresi¶on podemos despejar B que es lo ¶unico que no conocemos (la direcci¶on y
sentido de ~B
se conocen, y se pueden obtener usando la regla de la mano derecha1
y as¶³
B =
¹0I
2¼r
:
Queda ¶unicamente darse cuenta de que I es, tal y como pide el teorema de Ampµere,
la intensidad que cruza la super¯cie limitada por nuestra trayectoria.
16.5.4. Campo producido por una espira en su eje
Se va a calcular el campo que produce una espira circular en un punto del eje
que diste una distancia R del centro de la espira, si circulara por dicha espira una
intensidad I. No es un c¶alculo sencillo y tendremos que utilizar la ley de Biot-
Savart expresada en (16.3) Vamos a proceder tambi¶en usando la simetr¶³a, para
facilitar el c¶alculo de la expresi¶on. El producto de d~l
¢ ~r podr¶a descomponerse en
dos componentes, una paralela al eje y otra perpendicular a ¶el. Las componentes
perpendiculares se anulan unas con otras y por tanto nos bastar¶a con conocer cual
va a ser la componente paralela, ya que la otra ser¶a nula. Todo esto puede verse en
la ¯gura 16.1.
1Tomando la mano con el pulgar se~nalando en la direcci¶on de la corriente, el resto de los dedos
marcan cual es el sentido del campo el¶ectrico

I
B
Figura 16.2: Trayectoria para un solenoide in¯nito.
Debemos calcular por tanto ¶unicamente las componentes dBx paralelas al eje.
Esto ser¶a
dBx = dB sin µ = dB
µ
R
px2 + R2
¶
que, utilizando Biot y Savart ser¶a
dBx =
¹0
4¼
Idl
x2 + R2
R
px2 + R2
:
Para determinar ahora el campo debido a la espira completa bastar¶a integrar la
expresi¶on anterior alrededor de la espira:
Bx =
I
dBx =
I
¹0
4¼
IR
(x2 + r2)
3
2
dl
y, como x y R no van a variar2 la expresi¶on anterior puede tomarse como
Bx =
¹0IR
4¼ (x2 + r2)
3
2
I
dl
donde la integral de dl alrededor de la espira es 2¼r. Por tanto
Bx =
¹0
4¼
2¼R2I
(x2 + R2)
3
2
Nota ¦ La ecuacio¶n para el campo en el centro de la espira se deduce de la
anterior muy sencillamente y es
B =
¹0I
2R
;
cosa que el lector interesado puede entretenerse en demostrar.
16.5.5. Campo magn¶etico en el interior de un solenoide in¯-
nito
Se llama solenoide a un conjunto de espiras arrolladas consecutivamente. Para
calcular el campo magn¶etico de un solenoide habr¶³a que proceder m¶as rigurosamente
de lo que se va a hacer en este apartado pero, en aras a conseguir cierta claridad,
vamos a hacer ciertas aproximaciones fuertes y algunas tropel¶³as matem¶aticas.
2x ser¶a la distancia desde el centro hasta donde queremos tomar el punto, y R el radio de la
espira. Ambas magnitudes son constantes.

~Concretamente vamos B
a tomar un solenoide in¯nito enrollado de tal forma que
haya un total de n vueltas por unidad de longitud. Tomemos entonces el recorrido
insinuado en la ¯gura 16.2 que es un tanto peculiar. Dicho recorrido pasa por el
centro de la espira in¯nita para luego salir y alejarse hasta el in¯nito, donde se cierra
el circuito. Reconocemos que este recorrido no deja de ser peculiar, pero nos va a
llevar correctamente a la expresion ¶deseada si nos abstenemos de hacer preguntas
sobre la rigurosidad de esta demostracion. ¶Evidentemente en el in¯nito el campo sera ¶nulo, porque R
la perturbacion ¶de la espira no llega hasta tan lejos, con lo cual
la integral
~B
¢~l
va a ser nula en esta parte del recorrido. A su vez en los bordes de
este solenoide (en el casi en el cual un solenoide in¯nito tuviera bordes) el campo
va a ser perpendicular al recorrido. Por qu¶e?, por simetr¶³a es l¶ogico suponer que
el campo ~B
va a ser paralelo al solenoide en su interior y, si existiere en el exterior,
tambi¶en deber¶³a ser paralelo. Por tanto ¶unicamente quedar¶a hallar la integral en el
recorrido que discurre por el interior del solenoide. Esta integral ser¶a
I
~B
d~l
= BL
donde L es la longitud del solenoide (si, pese a todo sabemos que L = 1, pero
es ¶util ponerlo as¶³). Y cu¶anto ser¶a I, la intensidad total que atraviesa el plano?.
Como tenemos n espiras por unidad de longitud de solenoide, la corriente total que
atraviesa el plano limitado por esta singular trayectoria ser¶a Itotal = LnI. As¶³ pues
tendremos que
¹0LnI = BL
con lo cual
B = ¹0nI:
Esta es la expresi¶on del campo en el interior de un solenoide in¯nito. Su inter¶es
radica en que es tambi¶en una buena expresi¶on para el campo magn¶etico que existe
en el interior de un solenoide ¯nito, siempre que nos encontremos lejos de los bordes.
16.5.6. Fuerzas entre corrientes paralelas
C¶omo podemos calcular la fuerza con que se atraen (o repelen) dos corrientes
paralelas?. Para ello combinaremos las expresiones usadas en los apartados 16.5.3
y 16.5.2. Tomando el primer hilo, con una corriente el¶ectrica I1, crear¶a en un hilo
conductor, situado paralelamente a una 1distancia d de ¶el, un campo que, usando
16.5.3 ser¶a
B =
¹0I1
2¼d
;
y claro est¶a, este hilo segundo por el cual circula una corriente I2 experimentar¶a una
fuerza por estar sometido a este campo. Esta fuerza la tomamos de 16.5.2 y es
F = I2LB:
Ahora bien, como la longitud de ambos hilos es in¯nita, la fuerza total que sienten
estos hilos tambi¶en es in¯nita, aunque eso s¶³, repartida por su longitud sin l¶³mite.
Una magnitud ¶util es ver cuanta fuerza se siente por unidad de longitud L, lo que
equivale a decir que
F
l
= I2B =
¹0
2¼
I1I2
d
:
Respecto al sentido de la fuerza, se puede ver que ¶esta es atractiva cuando las
corrientes son en sentidos contrarios y repulsiva si el sentido es el mismo. Una forma
de verlo es considerando el sentido del campo en cada hilo y aplicando entonces que
~F = I~l
^ ~B
, o bien la llamada regla de la mano izquierda.

¦ Es frecuente utilizar estas relaciones para de¯nir el Amperio. 1 Amperio Nota
ser¶³a as¶³ la intensidad de corriente necesaria para que dos hilos rectos situados
a 1 metro el uno respecto al otro sientan una fuerza por unidad de longitud
equivalente a 2 ¢ 10¡7N
m.

Cap¶³tulo 17
Inducci¶on electromagn¶etica
La uni¶on de la electricidad y el magnetismo queda patente cuando descubrimos
que una intensidad el¶ectrica es capaz de crear un campo magn¶etico a su alrededor.
No obstante la f¶³sica es una ciencia en la que el pensamiento sim¶etrico resulta fre-cuentemente
ampliamente productivo, es decir, podemos preguntarnos Y podr¶a un
campo magn¶etico producir un fen¶omeno el¶ectrico?. La respuesta a esta pregunta es
a¯rmativa, como veremos a continuaci¶on.
17.2. Ley de Faraday-Henry
Si uno conecta un galvan¶ometro a una bobina de conductor, sin nada m¶as, el
galvan¶ometro no deber¶a se~nalar nada: por all¶³ no circula corriente de ning¶un tipo.
Pero ahora bien, al acercar o alejar un im¶an de la bobina descubrir¶³a un hecho sor-prendente:
el galvan¶ometro marcar¶³a una tenue corriente durante este proceso. Esta
experiencia, similar a las llamadas experiencias de Faraday, demuestra claramente
que existe una relaci¶on entre el campo magn¶etico y el el¶ectrico.
Si en la experiencia anterior uno acerca un im¶an a la bobina y lo deja ah¶³ ver¶³a
que el galvan¶ometro marca corriente mientras el im¶an se mueve, pero no cuando le
dejamos quieto. Este fen¶omeno constituye la esencia de la ley de Faraday y Henry,
que podemos ya enunciar:
² = ¡
dÁB
dt
: (17.1)
En esta ecuaci¶on ² es la fuerza electromotriz inducida y ÁB es el °ujo magn¶eti-co
que atraviesa la super¯cie delimitada por el circuito. As¶³ pues la variaci¶on del
°ujo magn¶etico ocasiona la aparici¶on de una fuerza electromotriz. Como el °ujo
magn¶etico ÁB = ~B
¢ ~S
esta variaci¶on puede deberse a tres causas diferenciadas o a
una mezcla de todas:
1. Variaci¶on del m¶odulo del campo magn¶etico B.
2. Variaci¶on del m¶odulo de la super¯cie del circuito S.
3. Variaci¶on de la orientaci¶on entre ambos.
. La variaci¶on del °ujo magn¶etico induce una fuerza electromotriz. Recuerda
109

CAP¶ITULO 17. INDUCCI¶ON ELECTROMAGN¶ETICA
17.2.1. Ley de Lenz
Y qu¶e signi¯ca el signo menos en la expresi¶on (17.1)?. ¶Este puede deducirse de
un principio f¶³sico m¶as general, conocido con el nombre de Ley de Lenz que a¯rma
que la fuerza electromotriz inducida posee una direcci¶on y sentido tal que tiende
a oponerse a la variaci¶on que la produce.
Este principio es una manera m¶as elegante de adivinar c¶omo ser¶a la f.e.m.
inducida en un circuito. Por ejemplo, supongamos que tomamos una espira con-ductora
e introducimos en ella un im¶an. En este caso el °ujo magn¶etico aumenta,
lo cual produce una f.e.m. inducida. Qu¶e sentido tendr¶a?. Aquel que se oponga a
la causa que lo produce, es decir, como en este caso es producido por un aumento
del °ujo magn¶etico el circuito tender¶a a disminuir dicho °ujo magn¶etico. Y c¶omo
puede lograrse esto?. Haciendo que la intensidad de corriente creada genere a su vez
un campo magn¶etico que se oponga al anterior y disminuyendo de esta manera el
campo.
De alguna manera este es un mecanismo de inercia que, en general, presentan
todos los sistemas f¶³sicos.
17.3. Fuerza electromotriz
En general para que en un circuito exista un corriente el¶ectrica estacionaria debe
existir un elemento que suministre esta energ¶³a a las cargas. Este elemento puede
ser, por ejemplo, una pila o bien un campo magn¶etico variable.
Se de¯ne as¶³ la fuerza electromotriz como el trabajo realizado por unidad de
carga realizado a lo largo del circuito; como el trabajo por unidad de carga es el
campo el¶ectrico tendremos que:
² =
l ~¢ dde¯niendo la integral a lo largo del circuito. Se ve de esta de¯nicion ¶que su unidad
va a ser el Voltio, al igual que el potencial el¶ectrico.
I
~E
Nota ¦ Entonces por que no llamar tambi¶en V a la fuerza electromotriz?.
Cuando tenemos un campo est¶atico, por ser conservativo resulta que
I
~E
¢ d~l
= 0
lo cual nos permit¶³a de¯nir el potencial el¶ectrico. Ahora bien, ahora el campo
el¶ectrico no resulta ser conservativo y por lo tanto no podemos de¯nir un
potencial, con lo cual aunque ² y V sean magnitudes similares que se miden
en la misma unidad, no obstante no son la misma cosa.
17.4. Autoinducci¶on
Imaginemos ahora que tenemos un circuito el¶ectrico apagado, con el interruptor
de corriente abierto. Qu¶e sucede cuando lo encendemos?.
Puede parecernos que simplemente se crea instant¶aneamente una corriente en
su interior igual a, seg¶un la ley de Ohm, I = V
R pero la realidad no es tan simple. Al
encender el circuito empieza a aumentar la intensidad por su interior, lo cual genera
un campo el¶ectrico que atraviesa el propio circuito. Este campo es proporcional a
la intensidad y por tanto var¶³a junto con la intensidad. La variaci¶on del campo
crea una variaci¶on del °ujo magn¶etico, y por lo tanto la aparici¶on de una fuerza
electromotriz inducida que se opone a esta intensidad creada. Por tanto el circuito
presenta una cierta inercia a ser arrancado.

e
R L
Figura 17.1: Circuito con una resistencia y una autoinducci¶on.
Ahora bien: C¶omo podemos relacionar el °ujo magn¶etico que el circuito crea
sobre s¶³ mismo?. En principio como el °ujo de un circuito, si no se deforma, va a
resultar proporcional al campo magn¶etico, y este es proporcional a la intensidad,
tendremos que el °ujo que el circuito genera sobre s¶³ mismo va a ser proporcional a
la intensidad. Esta constante de proporcionalidad se denomina la autoinducci¶on L
, y se tiene
Á = LI
. La unidad de autoinducci¶on en el Sistema Internacional es el henrio (H), equiva-lente
a 1H = 1s.
17.4.1. Inducci¶on mutua
De una manera an¶aloga a la anterior si tenemos dos circuitos pr¶oximos uno de
ellos puede inducir un cierto °ujo magn¶etico en el otro (y al rev¶es). El °ujo magn¶eti-co
que atraviesa el primer circuito, llam¶emosle a debido a la corriente el¶ectrica que
circula por b ser¶a proporcional a ¶esta, y por tanto
Áa = MabIb:
Este coe¯ciente M presenta tambi¶en las mismas unidades que L, el henrio, y se
llama inductancia mutua.
¦ An¶alogamente se tendr¶a que phib = MbaIa donde, adem¶as, se puede Nota
demostrar que Mab = Mba, una prueba m¶as de las simetr¶³as tan comunes en
f¶³sica.
17.5. Energ¶³a magn¶etica
Deducir la expresi¶on de la energ¶³a magn¶etica de forma directa no es sencillo, pero
en cambio se puede obtener un resultado muy util ¶utilizando argumentos indirectos
en los que la conservacion ¶de la energ¶³a juega su papel. Supongamos que tenemos
el circuito de la ¯gura 17.1 y analicemos que esta sucediendo. Por la ley P
de Ohm el
efecto de todas las fuerzas electromotrices es generar una IR, es decir,
² = IR.
Podemos atribuir una ² a la pila y una ²0 a la f.e.m. que se induce en el circuito.
Sabemos que ²0 = ¡dÁ
y que para un propio circuito Á = LI siendo L una constante.
dt Tendremos por tanto que
² + ²0 = IR ) ² ¡ L
dI
dt
= IR;

y despejando de aqu¶³ la f.e.m. que produce la pila, es decir, ² resultar¶a que
² = IR + L
dI
dt
: (17.2)
Sabemos ahora que ²I es toda la potencia que suministra la pila. Multipliquemos
entonces toda la ecuaci¶on (17.2) por I para ver a donde va a para esa potencia y
tendremos que
²I = I2R + LI
dI
dt
;
es decir, que parte de la potencia se gasta en el efecto Joule (producir calor) y otra
parte se va en el t¶ermino LI dI
dt . Como la potencia es P = dE
dt si llamamos EB a
la energ¶³a asociada con el campo magn¶etico que se almacena en la autoinducci¶on
tendremos que
dEB
dt
= LI
dI
dt
de donde integrando se tiene que
EB =
1
2
LI2:
Ampliacio¶n ± La expresio¶n general del campo magn¶etico contenido en una regio¶n del
espacio en funci¶on de B es m¶as dif¶³cil de obtener y tiene el siguiente aspecto:
EB =
1
2¹0
Z
V
B2dV:
17.6. Problemas y aplicaciones de inducci¶on elec-tromagn
¶etica
17.6.1. Generadores
Un generador es un dispositivo capaz de producir corriente a partir de otras
formas de energ¶³a, generalmente a partir de energ¶³a mec¶anica.
La gran mayor¶³a de los generadores consisten en una espira conductora que gira
en el interior de un campo magn¶etico constante y homog¶eneo a velocidad angular
! tambi¶en constante. C¶omo ser¶a su fuerza electromotriz inducida?.
El °ujo magn¶etico que atraviesa la espira ser¶a igual a Á = ~B
¢ ~S
= BS cos µ.
En este caso si la espira gira a una velocidad angular constante, esto supondr¶a que
µ = !t + Á siendo Á una fase inicial que podemos suponer tranquilamente que es
cero. Tendremos por tanto que Á = BS cos(!t).
Para calcular ² sabemos que ² = ¡dÁ
dt con lo cual directamente obtenemos que
² = BS! sin(!t).
En la pr¶actica se usan solenoides con muchas espiras y otras mejoras t¶ecnicas,
pero en cualquier caso la f.e.m. producida siempre es del tipo ² = ²0 sin(!t).
Nota ¦ Si representamos la f.e.m. inducida en este tipo de generadores en fun-ci
¶on del tiempo, como en la ¯gura 17.2 vemos que esta corriente generada es
alterna. Esta es una de las razones por las que el uso de la corriente alterna
est¶a tan difundido: ya que su generaci¶on es mucho m¶as sencilla que la de la
corriente continua.

t
e
Figura 17.2: Corriente alterna.
17.6.2. Transformadores
Un transformador es un aparato capaz de cambiar el voltaje o tensi¶on de la
corriente el¶ectrica alterna. B¶asicamente est¶an formados por dos solenoides de n1 y
n2 espiras arrollados en torno a un n¶ucleo de hierro, como en la ¯gura 17.3. Si uno
de estos circuitos es alimentado por un generador que produce una f.e.m. ²1 esto
producir¶a un °ujo magn¶etico Á que atravesar¶a cada espira del solenoide. En este
circuito, si suponemos que no se pierde energ¶³a en calor, etc. . . tendremos que toda
su ²1 se est¶a invirtiendo en °ujo magn¶etico y, seg¶un (17.1) y como el °ujo total
que atraviesa el circuito es el de una espira, Á por todas las n1 espiras que tiene se
obtiene que
²1 = ¡n1
dÁ
dt
:
Veamos que sucede para el circuito 2. El hecho de arrollar ambos circuitos a
un n¶ucleo de hierro sirve para que casi todo el °ujo (siempre se pierde algo) Á que
atravesaba cada espira del primer circuito lo haga tambi¶en en las del segundo. De
esta manera vamos a suponer que no hay p¶erdida alguna y que, tambi¶en para el
segundo circuito cada espira es atravesada por el °ujo Á. En este caso se inducir¶a una
corriente ²2 equivalente a la derivada temporal del °ujo total con signo menos, esto
es
²2 = ¡n2
dÁ
dt
y como el t¶ermino dÁ
dt es el mismo en ambas expresiones si dividimos miembro a
miembro tenemos que
²2 =
n2
n1
²1
que nos da la relaci¶on entre las tensiones de entrada y salida de un transformador.
Ahora bien, este no es un dispositivo milagroso y aunque logra transformar
un tenue voltaje en otro m¶as alto debe respetar el principio de conservaci¶on de
la energ¶³a, y por tanto las potencias de entrada y salida deber¶³an ser, si no hay
p¶erdidas1 iguales. Como la potencia es P = I² esto nos dice que las intensidades se
transforman como I2 = n1
n2
I1.
Resumiendo: Si elevamos la tensi¶on de un circuito lo hacemos a costa de dis-minuir
su intensidad. Cuando bajamos la tensi¶on de otro a cambio elevamos la
intensidad. La potencia, que es el t¶ermino energ¶etico, se mantiene constante.
1En un caso real la potencia de salida siempre es menor que la de entrada, el resto se disipa en
forma de calor.

n
n
1
2
e
e1
2
Nucleo de hierro.
Figura 17.3: Esquema simpli¯cado de un transformador.
17.6.3. Autoinducci¶on de un solenoide
Si tomamos la aproximaci¶on de solenoide muy largo que vimos en el apartado
16.5.5 podemos intentar calcular el valor de su coe¯ciente de autoinducci¶on. Como el
campo en su interior vale B = ¹0nI siendo n, recordemos, la densidad longitudinal
de espiras, tendremos que si cada espira presenta una super¯cie S el °ujo total
ser¶a ÁT = nlBS donde l es la longitud del solenoide. Despejando
L =
ÁT
I
y por tanto en esta aproximaci¶on resultar¶a que
L = ¹0n2lS:

Cap¶³tulo 18
La naturaleza de la luz.
Dualidad onda corp¶usculo de
la materia
18.1. Introducci¶on hist¶orica
Hist¶oricamente la luz ha sido siempre un ente escurridizo al que los f¶³sicos han
querido asignar una naturaleza determinada, sin conseguirlo. Newton, a ¯nales del
siglo XVII, sostuvo que la luz estaba compuesta por part¶³culas, diferentes seg¶un el
color, y que rebotaban en un espejo logrando as¶³ explicar porqu¶e los ¶angulos de
incidencia y re°exi¶on eran los mismos. Parece ser que la propagaci¶on rectil¶³nea de
la luz tuvo mucho que ver con esta posici¶on. Adem¶as lograba explicar la refracci¶on
sobre la super¯cie de dos medios diferentes usando tambi¶en una teor¶³a corpuscular.
Huygens, contempor¶aneo de Newton, hablaba de ondas luminosas, y mediante el
principio de Huygens, visto en 15.2 explicaba tambi¶en la refracci¶on y re°exi¶on.
Seg¶un Newton la luz deb¶³a ir m¶as r¶apida en un medio m¶as denso. Seg¶un Huygens el
fen¶omeno era al rev¶es, pero no obstante en aquella ¶epoca a¶un no se pod¶³a medir la
velocidad de la luz de manera ¯able, y no se lev¶o a cabo ning¶un experimento para
descubrir quien ten¶³a raz¶on; fue la eminencia de Newton lo que decant¶o la balanza
hacia el lado corpuscular de la luz durante esa ¶epoca, y esta inercia hizo que, pese
a los continuos debates y pol¶emicas, fuera la naturaleza corpuscular de la luz la
dominante durante el siglo siguiente al de Newton.
A principios del siglo XIX empez¶o a formarse un sistema consecuente y desarro-llado
de la luz vista desde un punto ondulatorio. Fueron de gran importancia las
aportaciones de Joung y Fresnel. El descubrimiento de muchos fen¶omenos de difrac-ci
¶on e interferencia relacionados con la luz y la posterior explicaci¶on del fen¶omeno
ondulatorio de la luz como una onda electrom¶agnetica por parte de Maxwell pare-ci
¶o dejar sentada de¯nitivamente la teor¶³a ondulatoria sobre la luz a ¯nales del siglo
XIX.
Pero no obstante a ¯nales del siglo XX surge uno de los fen¶omenos m¶as com-plejos
y enrevesados estudiados entonces: la radiaci¶on del cuerpo negro: un sistema
ideal que absorbe toda la radiaci¶on que incide sobre ¶el y que, en buena aproxima-ci
¶on, puede tomarse como un cuerpo con una cavidad que comunica con el exterior
con un peque~no ori¯cio, y cuyas caracter¶³sticas radiativas cumplen la propiedad de
depender s¶olo de la temperatura de sus paredes.
Fue este hecho el que jug¶o un papel primordial en la historia de la f¶³sica moderna
y que oblig¶o a Planck (a disgusto, seg¶un cuenta la historia) en 1.900 a introducir
115

CAP¶ITULO 18. LA NATURALEZA DE LA LUZ. DUALIDAD ONDA CORP¶USCULO DE LA
MATERIA
Figura 18.1: Dibujo de un cuerpo negro.
x**3/(exp(x)-1)
x**3/(exp(1.2*x)-1)
x**3/(exp(1.1*x)-1)
n
E
Figura 18.2: Distribuci¶on espectral de la radiaci¶on emitida por un cuerpo negro a
distintas temperaturas.
uno de los fen¶omenos m¶as sorprendentes de la f¶³sica: la cuantizaci¶on de la energ¶³a
y, en concreto, de la luz.
18.2. El cuerpo negro
Un esquema de la cavidad que puede aproximarse a un cuerpo negro ideal se
encuentra en la ¯gura 18.1. Estos cuerpos al irse calentando van encontrando un
equilibrio de radiaci¶on en el cual, a mayor temperatura, el cuerpo emite a su vez m¶as
radiaci¶on. Adem¶as al irse calentando el cuerpo aumenta la cantidad de energ¶³a ra-diada
(de acuerdo con la ley de Stefan-Boltzmann) y la concentraci¶on de la energ¶³a
se desplaza hacia longitudes de ondas m¶as cortas. Precisamente a una represen-taci
¶on de la potencia radiada frente a la longitud de onda se le puede denominar
distribuci¶on de la radiaci¶on o distribuci¶on espectral.
Una gr¶a¯ca de la distribuci¶on espectral de la radiaci¶on de un cuerpo negro
puede verse en la ¯gura 18.2. Este resultado experimental se intent¶o explicar de
una forma directa a partir de la termodin¶amica cl¶asica, y el resultado obtenido, que
tambi¶en est¶a representado en la ¯gura 18.2, claramente no coincid¶³a con el resultado
verdadero, que es siempre el que marca la experiencia de laboratorio.
En 1900 el f¶³sico alem¶an, Max Planck a¯rm¶o que realizando una inusitada modi-
¯caci¶on de los c¶alculos cl¶asicos, e introduciendo una hip¶otesis nueva y singularmente

MATERIA
extra~na, hab¶³a encontrado una distribuci¶on espectral que explicaba perfectamente
los datos experimentales.
Esta sorprendente hip¶otesis era que la energ¶³a emitida y absorbida por el
cuerpo no era continua, es decir, el cuerpo no pod¶³a tomar o dejar cualquier valor
de ¶esta, sino discreta y adem¶as, proporcional a la frecuencia. Es decir
E = hº (18.1)
donde h es la constante de proporcionalidad, de valor h06;626¢10¤¡34 Js y conocida
actualmente como constante de Planck.
Planck fue absolutamente incapaz de encajar esta hip¶otesis dentro del marco de
la mec¶anica cl¶asica y, sin propon¶erselo, hab¶³a dado el primer paso para el adveni-miento
de la mec¶anica cu¶antica.
. La radiaci¶on electromagn¶etica se emite en paquetes de energ¶³a o Recuerda
fotones cuyo valor energ¶etico es:
E = hº:
18.3. El efecto fotoel¶ectrico
18.3.1. Descripci¶on del problema
Este efecto fue descubierto por Hertz en 1.887 y estudiado por Lenard en 1.900.
Fue satisfactoriamente explicado por Einstein en 1.905 y su explicaci¶on le supuso
ganar el Premio Nobel de F¶³sica. El efecto fotoel¶ectrico consiste en el hecho de que,
cuando se ilumina una super¯cie met¶alica limpia, bajo ciertas condiciones se emiten
electrones. Estos electrones pueden ser recogidos en un tubo de rayos cat¶odicos para
relacionar su emisi¶on con algo f¶acilmente medible, como es la intensidad y voltaje
el¶ectrico.
Analicemos que sucede en el circuito de la ¯gura 18.3. Cuando la luz incide
sobre el c¶atodo C se emiten electrones. Si alguno de ellos choca con el ¶anodo A
existir¶a una cierta corriente por el circuito. El n¶umero de electrones emitidos que
alcanzan el ¶anodo puede variarse haciendo el ¶anodo positivo o negativo respecto
el c¶atodo, es decir, creando una diferencia de potencial V entre ellos. Cuando V
es positivo los electrones arrancados por la luz son atra¶³dos por el ¶anodo. Para
un valor lo su¯cientemente alto de V todos los electrones arrancados por la luz
alcanzan el ¶anodo y la corriente logra su valor m¶aximo; si aumentamos m¶as V
descubriremos que que la corriente ya no aumenta, se mantiene en su valor m¶aximo,
ya que V no in°uye en que se liberen m¶as electrones del c¶atodo, sino s¶olo en que
todos los que son liberados se acerquen hacia el ¶anodo. Si variamos V al rev¶es
los electrones ser¶an repelidos por el ¶anodo, y s¶olo aquellos que tengan una energ¶³a
cin¶etica ( 1
2mv2) su¯cientemente alta lograr¶an llegar al ¶anodo y generar corriente.
Pero ahora bien, cuando bajamos V y lo hacemos menor que un cierto valor ¡V0
no existe corriente alguna, lo cual signi¯ca que ning¶un electr¶on alcanza el ¶anodo.
Entonces este potencial V0 estar¶a relacionado con la m¶axima energ¶³a cin¶etica que
tendr¶an los electrones, de manera que podemos poner
1
2
mv2jmax = eV0:
Ahora bien y qu¶e es lo interesante de esta experiencia?. Lo curioso es que
el valor de V0 no depende de la intensidad de la radiaci¶on, pero si depende de
algo tan peregrino como el color de la luz con que se ilumine el c¶atodo. As¶³ pues
aparentemente al aumentar la intensidad, por tanto la energ¶³a por unidad de tiempo

MATERIA
A
Luz
anodo catodo
+ -
electrones
Figura 18.3: Dispositivo simpli¯cado para la medici¶on del efecto fotoel¶ectrico.
que cae sobre el c¶atodo, no aumenta la energ¶³a cin¶etica de los electrones emitidos.
C¶omo se puede explicar esto?. Por qu¶e sucede?. Estas fueron las preguntas que
se hizo Einstein ( y logr¶o contestar) en 1.905.
18.3.2. Soluci¶on
Einstein demostr¶o que estas experiencias pod¶³an entenderse suponiendo que la
energ¶³a luminosa no se distribuye de manera continua, como dice el modelo cl¶asico
( y Maxwelliano) de la luz, sino cuantizada en paquetes peque~nos llamados fotones.
La energ¶³a de un fot¶on es E = hº, la relaci¶on que Planck us¶o para la explicaci¶on del
cuerpo negro. Einstein supuso que un electr¶on emitido desde la super¯cie del c¶atodo
es de alguna forma arrancado por el impacto con el fot¶on, de forma que toda la
energ¶³a del fot¶on pasa al electr¶on. Ahora bien, el electr¶on recibe su energ¶³a de un
¶unico fot¶on. As¶³, cuando se aumenta la intensidad de la luz lo que sucede es que
al incidir m¶as fotones sobre el c¶atodo por unidad de tiempo quedan m¶as electrones
liberados, pero la energ¶³a que ha absorbido cada electr¶on no var¶³a, es la misma.
De esta manera se hace un sencillo c¶alculo energ¶etico: Si la energ¶³a necesaria
para que se desprenda un electr¶on de la super¯cie de un metal es, pongamos, una
cierta W, la energ¶³a m¶axima de los electrones deber¶³a ser la que queda de la que
ten¶³a el electr¶on, es decir
1
2
mv2jmax = hº ¡W
y como a su vez, sab¶³amos que esta energ¶³a era eV0 podemos deducir que este
potencial de frenado V0 ser¶a
V =
hº ¡W
e
:
Este resultado coincid¶³a plenamente con los datos experimentales, y adem¶as el
valor h de la constante h result¶o ser igual que el usado por Planck para explicar

MATERIA
el cuerpo negro. Esto supuso una nueva evidencia sobre la validez universal de la
hip¶otesis de la cuanti¯caci¶on de la energ¶³a lum¶³nica.
18.4. Efecto Compton
Arthur H. Compton, en 1.923 realiz¶o una experiencia en la que se enviaban rayos
X (un tipo de luz m¶as energ¶etica que la visible) a una zona con ¶atomos, y posterior-mente
se med¶³a tanto la frecuencia y ¶angulo de la luz dispersada como la velocidad
el electr¶on derivado tras el choque. Utilizando los principios de conservaci¶on de la
energ¶³a y del momento lineal en estos choques, todos los resultados eran coherentes
si se supon¶³a que la luz se comportaba como una part¶³cula (un fot¶on) que colisiona
con el electr¶on, con energ¶³a dada por la relaci¶on de Planck E = hº y con momento
lineal igual a
p =
h
¸
: (18.2)
¦ Puede resultar ¶util recordar que, de acuerdo con la teor¶³a cl¶asica, la Nota
energ¶³a y cantidad de movimiento de una onda electromagn¶etica est¶a marcada
por
E = pc;
entonces, relacionando esta E mediante la ecuaci¶on (18.1) y recordando que
c = ¸º se obtiene f¶acilmente (18.2).
18.5. Naturaleza ondulatoria de la materia
Las ideas de simetr¶³a, que se muestran siempre muy ¶utiles en la f¶³sica, levaron a
Louis de Broglie a pensar que, al igual que la luz, pese a ser de naturaleza supues-tamente
ondulatoria, presentaba muchas veces una componente corpuscular, pod¶³a
ser que la materia normal, tratada siempre como part¶³cula, tuviese tambi¶en una
naturaleza ondulatoria.
Pero de Broglie fue m¶as all¶a: si el momento lineal de un fot¶on, seg¶un el expe-rimento
de Compton, era p = h
¸ por qu¶e no utilizar esta relaci¶on para encontrar
la longitud de onda de la materia?. Esto es, para un cuerpo normal p = mv y
usando (18.2) y despejando as¶³ ¸ obtenemos
¸ =
h
mv
: (18.3)
Ahora bien, la f¶³sica tiene siempre una forma para decidir cuando una hip¶otesis
es o no correcta: la experimentaci¶on. En experiencias posteriores se pudo compro-bar
que efectivamente, part¶³culas como los electrones, pueden producir patrones de
difracci¶on, un hecho puramente ondulatorio, similares a los que producen los rayos
X.
Ahora bien, si todas las part¶³culas presentan esta dualidad onda y corp¶usculo,
por qu¶e en nuestra vida cotidiana no vemos, por ejemplo, la difracci¶on de una
bola de billar o de alg¶un objeto igualmente macrosc¶opico?. La respuesta es que, si
tomamos una bola de billar con una masa de 100 gramos y una velocidad de 1m
s su
longitud de onda ser¶a, dado el ¶³n¯mo valor de h, extremadamente peque~na, raz¶on
por la cual con los aparatos actuales somos incapaces de comprobar su existencia.
Para objetos m¶as peque~nos (protones, electrones, neutrinos. . . ) se ha encontrado
un comportamiento ondulatorio siempre que se ha buscado.
± Evidentemente toda esta serie de fen¶omenos nuevo invalida de tal ma- Ampliaci¶on
nera las leyes anteriores que es necesaria la b¶usqueda de nuevas leyes de

MATERIA
Newton, de nuevas ecuaciones que sean capaces de explicar a su vez estos
nuevos fen¶omenos. Estas nuevas leyes entran a formar parte de un nuevo mar-co
de la f¶³sica que se conoce como F¶³sica Cu¶antica o Mec¶anica Cu¶antica. La
palabra cu¶antica hace referencia al hecho de que, en este nuevo marco, algu-nas
magnitudes no van a ser continuas, sino que van a ser discretas, a estar
cuantizadas, es decir, a permitir s¶olo ciertos valores discretos.
Podemos citar a los f¶³sicos SchrÄodinger, Heisemberg y Pauli como los pa-dres
de la mec¶anica cu¶antica, descubridores a su vez respectivamente de la
mec¶anica de matrices, la ecuaci¶on de SchrÄodinger de la Mec¶anica Cu¶antica y
la ecuaci¶on de Pauli de la Mec¶anica Cu¶antica y Relativista (en la cual aparece
de manera natural el fen¶omenos del esp¶³n), pero toda lista ser¶³a incomple-ta.
La Mec¶anica Cu¶antica y la Mec¶anica Relativista son dos espectaculares
teor¶³as, en su mayor¶³a poco intuitivas e incluso muchas veces contra el sentido
com¶un que han revolucionado la f¶³sica del siglo XX y han logrado explicar
in¯nidad de hechos nuevos y otros ya conocidos bajo una luz diferente. Su
uni¶on con las teor¶³as de campos, en lo que se conoce como Teor¶³a Cu¶antica de
Campos ha dado pie a una de las teor¶³as m¶as exactas y extra~nas que existen
actualmente.
Tecnol¶ogicamente aparatos tan cotidianos como los ordenadores o avances
m¶edicos como la radiolog¶³a no habr¶³an sido posibles sin estos descubrimientos.
18.6. Resumen: Dualidad onda-corp¶usculo de la
luz y la materia
As¶³ pues como resumen qu¶e es la luz y la materia? Son ondas o son part¶³culas?
Se comportan como las primeras o las segundas?. Como se ha podido ir desgajando
a lo largo de las secciones la respuesta no es f¶acil. La f¶³sica en s¶³ misma no es una
ciencia que pretenda explicar la esencia de la Naturaleza, sino m¶as bien c¶omo se
comporta ¶esta. Por eso la contestaci¶on a la pregunta de si la luz es onda o es part¶³cula
es irrelevante. Lo importante es que, seg¶un la experiencia, se comporta de una u
otra forma en unos u otros casos. As¶³ mismo la materia se comporta como onda o
como corp¶usculo seg¶un la ocasi¶on. Ser¶³a como si fuera onda los lunes mi¶ercoles y
viernes y part¶³cula el resto.
No obstante quiz¶as esta explicaci¶on parezca muy absurda a muchos, que piensen
que todo esto tiene que estar claramente equivocado porque c¶omo va a ser algo
onda y part¶³cula a la vez?. Seg¶un los m¶as elementales principios de la l¶ogica algo
no puede ser y no ser a la vez, o bien un ente no puede contener dos propiedades
contradictorias de forma consecutiva.
El problema surge al considerar la esencia misma de la concepci¶on onda o
de la concepci¶on part¶³cula. La mente humana crea un modelo, un concepto como
onda para explicar una serie de hechos, y luego renuncia a los hechos para a¯rmar-se
m¶as en la concepci¶on de onda. An¶alogamente crea la concepci¶on part¶³cula.
Posteriormente cree que, el hecho de que ciertos aspectos de la Naturaleza puedan
explicarse como part¶³cula implican que ese aspecto es una part¶³cula, y esta identi-
¯caci¶on es la que resulta incorrecta. Por ejemplo: una bola de billar se comporta
como una part¶³cula, pero esto no signi¯ca que sea una part¶³cula. Qu¶e es por tanto
una bola de billar?. No es la f¶³sica quien tiene que dar la respuesta, entre otras
cosas porque (es mi opini¶on) ni es un tema de su incumbencia ni lo podr¶a saber
nunca. La bola de billar es un objeto incognoscible al que podemos asociar una
etiqueta part¶³cula porque en todas las ocasiones se comporta como tal, pero por
ello no tiene por qu¶e ser una part¶³cula. Dicho de otra forma, onda o part¶³cula
son s¶olo modelos o categor¶³as mentales, y la Naturaleza no tiene porqu¶e amoldarse
a nuestras aldeanas categor¶³as mentales. La Naturaleza ser¶a lo que sea, y muchas
facetas suyas se aproximar¶an a onda y otras a part¶³cula que no son m¶as que

MATERIA
aproximaciones o modelos humanos.
As¶³ pues qu¶e es un fot¶on? Qu¶e es la luz?. Conocer la esencia de la luz no
es tarea de la f¶³sica, su tarea es describir c¶omo se comporta la luz bajo ciertas
condiciones. Y de esta forma se descubre y estudia que a veces se comporta como
luz y a veces como part¶³cula, pero comportarse como es muy distinto de ser.
A¶un as¶³ ser¶³a interesante concluir citando unas palabras de Einstein: Lo mas
incomprensible es que sea comprensible.

MATERIA

Cap¶³tulo 19
Fundamentos de F¶³sica
Nuclear
La materia est¶a compuesta por ¶atomos, unidos entre s¶³ por enlaces qu¶³micos.
A su vez los ¶atomos est¶an compuestos de electrones, neutrones y protones, deno-min
¶andose a estos dos ¶ultimos el n¶ucleo at¶omico. Como los ¶atomos son neutros esto
obliga a que exista el mismo n¶umero de electrones que de protones en un ¶atomo
normal, ya que los neutrones no tiene carga y los protones y electrones tienen igual
carga pero de distinto signo.
Ahora bien qu¶e es un n¶ucleo? qu¶e pasa dentro de un n¶ucleo? puede variar el
n¶ucleo?. Estas son las preguntas que intentaremos responder.
19.2. El n¶ucleo at¶omico
19.2.1. Algunas de¯niciones
La masa de un n¶ucleo cualquiera se puede constatar que coincide muy bien
con un n¶umero entero de veces la masa del n¶ucleo del ¶atomo de hidr¶ogeno. Las
variaciones de masa de unos n¶ucleos a otros tambi¶en es un m¶ultiplo de la masa del
¶atomo de H. De esta manera se denomina A al n¶umero m¶asico de un ¶atomo, es
decir, precisamente al n¶umero que es ese m¶ultiplo del ¶atomo de H. De esta manera
claramente para el hidr¶ogeno A = 1.
Al n¶umero de protones que contiene un n¶ucleo, que como hemos dicho es el
mismo que electrones tiene su corteza, se le denomina Z. Como adem¶as la masa de
protones y neutrones es casi igual se tiene que el n¶umero de neutrones de un ¶atomo
es
N = A ¡ Z:
Un elemento qu¶³mico est¶a formado por un conjunto de ¶atomos con igual Z, pero
donde puede variar N. Por esta raz¶on se denomina is¶otopos a los ¶atomos del mismo
elemento pero de distinta masa, es decir, que necesariamente tienen que poseer un
n¶umero distinto de neutrones. Un n¶uclido es aquel conjunto de ¶atomos de igual
A y Z (y por tanto N) y se representa como AZ
X siendo X el s¶³mbolo qu¶³mico
del elemento correspondiente a su Z. Se ve f¶acilmente que en esta notaci¶on hay
informaci¶on redundante.
123

CAP¶ITULO 19. FUNDAMENTOS DE F¶ISICA NUCLEAR
El patr¶on de medida que se utiliza para las masas at¶omicas es la unidad de masa
at¶omica o u.m.a., se de¯ne como la doceava parte de la masa del 126C.
19.2.2. Caracter¶³sticas
Cuando se mide muy precisamente la masa del n¶ucleo resulta sorprendente com-probar
que ¶esta siempre es algo menor que la suma de las masas de las part¶³culas
que lo componen. Concretamente se puede restar la masa de las part¶³culas que lo
componen de su masa real y obtener as¶³
¢m = Zmp + (A ¡ Z)mn ¡ mX
siendo mX la masa real del ¶atomo de AZ
X.
Qu¶e ha sucedido con esta masa que se ha perdido?. Recordemos que seg¶un la
teor¶³a de la relatividad de Einstein masa y energ¶³a son intercambiables, por lo que
podemos a¯rmar que el n¶ucleo como tal tiene una energ¶³a E = ¢mc2 menor que las
part¶³culas que lo forman. Esta energ¶³a, por tanto, se desprendi¶o cuando se form¶o el
n¶ucleo y su carencia es lo que ahora posibilita su existencia como agregado. Si la
volvi¶eramos a reintegrar al n¶ucleo obtendr¶³amos otra vez los neutrones y protones
correspondientes y por tanto disgregar¶³amos el ¶atomo a sus componentes. Se trata
por tanto de la energ¶³a de enlace del n¶ucleo at¶omico.
Esta energ¶³a nuclear est¶a asociada a su vez a la fuerza nuclear fuerte, la inte-racci
¶on que evita que los protones se alejen (se repelen entre s¶³) manteni¶endoles
fuertemente unidos. Algunas propiedades de esta fuerza son:
Es de muy corto alcance, s¶olo se nota a distancia de un fermi (1 ¢ 10¡15m) o
menores.
No depende de la carga el¶ectrica.
Es una fuerza atractiva, aunque a distancias mucho m¶as peque~nas que su
alcance resulta repulsiva.
Depende del esp¶³n de los protones y neutrones que relaciona.
En cuanto al tama~no del n¶ucleo es del orden de 10¡15. Se ha encontrado que se
puede suponer a los n¶ucleos como esferas de radio
R = R0A
1
3
donde R0 = 1;2fm y A es el n¶umero m¶asico del n¶ucleo en cuesti¶on.
19.3. Radiactividad
La radiactividad es la emisi¶on de part¶³culas ®1, ¯2y °3 por parte de un n¶ucleo
at¶omico y como consecuencia de ajustes y cambios internos en los que general-mente
el n¶ucleo cambia su n¶umero de neutrones y protones (y por tanto pasa de
un elemento a otro). Hist¶oricamente la radiactividad fue descubierta por Becquerel
al descubrir que un compuesto que conten¶³a uranio era capaz de velar una placa
fotogr¶a¯ca sin necesidad de exponer ¶esta a la luz.
Antes de entrar en detalle en estos procesos radiactivos es interesante se~nalar
que en aquellos que se producen desintegraciones (reacciones at¶omicas) se conservan
la energ¶³a, el momento angular y el lineal y la carga, as¶³ como otras magnitudes
como conservar el n¶umero de protones m¶as neutrones (de nucleones).
1N¶ucleos de Helio.
2Positrones o electrones.
3Fotones muy energ¶eticos.

19.3.1. Radiactividad ®
En la radiaci¶on ® un n¶ucleo se desintegra emitiendo un n¶ucleo de Helio, que es
a lo que se denomina part¶³cula ®. De esta manera la reacci¶on que se establece es la
siguiente
A
ZX !A¡4
Z¡2 Y +42
He
en donde X era el n¶ucleo original e Y ser¶a el producto de la reacci¶on, cuyo n¶umero
at¶omico es dos unidades menor que el del original. Haciendo un c¶alculo de diferencias
de energ¶³a, la energ¶³a liberada en esta reacci¶on ser¶a
E = (MX ¡MY ¡M®)c2:
La radiactividad ® es muy poco penetrante. Basta una hoja de papel o un vestido
para pararla.
19.3.2. Radiactividad ¯
Existen dos tipos de radiactividad ¯, la ¯+ y la ¯¡ en cuyas reacciones se emiten
positrones y electrones, respectivamente. De esta manera procesos de este tipo dar¶an
lugar a reacciones como
Z+1 Y + ¯¡ + ¹º
A
ZX !A
y
Z¡1 Y + ¯+ + º
A
ZX !A
en donde ¹º y º son respectivamente un antineutrino y un neutrino, de los cuales
hablaremos m¶as tarde.
Experimentalmente se encontr¶o que la energ¶³a de los productos ¯nales no se co-rrespond
¶³a con la que se esperaba si s¶olo se emitieran un n¶ucleo hijo m¶as la part¶³cula
beta respectiva. Por esta raz¶on Pauli postul¶o la existencia de unas part¶³culas nue-vas,
de carga neutra (raz¶on que hac¶³a dif¶³cil su detenci¶on) y masa, caso de tener4,
muy peque~na (y por eso se le bautiz¶o neutrino, puesto que era como un neutr¶on
chiquit¶³n.
Posteriormente se descubri¶o que, efectivamente, esta part¶³cula existe.
La radiactividad beta es bastante penetrante, aunque se puede parar con una
l¶amina de metal.
19.3.3. Radiactividad °
La radiaci¶on ° consiste en la emisi¶on de fotones muy energ¶eticos. La raz¶on de la
existencia de esta radiaci¶on se debe a la necesidad de descargar parte de su energ¶³a
que tienen algunos n¶ucleos despu¶es de una desintegraci¶on en la que quedan en un
estado excitado. Este proceso es similar al de la emisi¶on de luz por parte de un
¶atomo normal (por ejemplo, uno de hidr¶ogeno) cuando los electrones caen de un
nivel excitado a otro m¶as fundamental. De esta manera el n¶ucleo tambi¶en tiene
algunos niveles energ¶eticos diferenciados entre los cuales puede moverse mediante
la emisi¶on de fotones. Como la diferencia entre niveles energ¶eticos de un n¶ucleo es
bastante cuantiosa, los fotones emitidos o part¶³culas gamma tienen energ¶³as muy
impresionantes.
Esta radiactividad es la m¶as peligrosa de todas por su alto poder de penetraci¶on
y por su elevado nivel energ¶etico. Para frenarla se requieren, en casos extremos,
planchas de plomo muy gruesas.
4Tras cuidadosas mediciones se ha logrado establecer, tras varios a~nos de duda, que la masa
del neutrino es muy peque~na pero distinta de cero.

19.4. Caracter¶³sticas de los procesos radiactivos
19.4.1. Cin¶etica de las reacciones nucleares: Ley de desinte-graci
¶on
Un n¶ucleo radiactivo posee una cierta probabilidad de desintegrarse. El hecho
de que estemos tratando con un proceso probabil¶³stico se debe a que la naturaleza
de la desintegraci¶on es fundamentalmente de tipo cu¶antico.
As¶³, la cantidad de n¶ucleso dN que se desintegran ser¶a proporcional al tiempo que
pasa dt y al n¶umero total de n¶ucleos que ten¶³amos, N. De esta manera obtenemos
que
dN = ¡¸Ndt
donde ¸ es una constante de proporcionalidad que se llama constante de desinte-graci
¶on.
Integrando y despejando convenientemente se demuestra que
N = N0e¡¸t (19.1)
donde N es el n¶umero de n¶ucleos radiactivos que quedan en una muestra cuando,
tomando una muestra original de N0 n¶ucleos dejamos transcurrir un tiempo t.
Tambi¶en se puede expresar este fen¶omeno en t¶erminos del periodo de semidesin-tegraci
¶on T1
2
, que se de¯ne como el intervalo de tiempo necesario para que en una
muestra el n¶umero de nucleos radiactivos se reduzca a la mitad.
De esta manera, el que al pasar un tiempo T1
2
tengamos una muestra que al
principio presentaba N0 n¶ucleos con s¶olo N0
2 supondr¶a que
N0
2
= N0e
T 1
2
y, por tanto
T1
2
=
ln2
¸ ¼
0;693
¸
:
Es usual tambi¶en hablar de la vida media ¿ de un n¶ucleo como el tiempo ne-cesario
para que el n¶umero N0 de n¶ucleos radiactivos de una muestra se reduzca a
N0
e . De esta manera se demuestra que
¿ =
1
¸
:
Por ¶ultimo se de¯ne la actividad de una muestra, cuya unidad en el S.I. es el
becquerel (Bq) como una desintegraci¶on por segundo. As¶³ actividad ser¶a
jdNj
dt
= N0¸e¡¸t:
19.4.2. Las series radiactivas
Una serie radiactiva es un conjunto de n¶uclidos radiactivos que derivan del mismo
n¶uclido inicial pero que, por desintegraciones consecutivas, conducen a un mismo
n¶uclido que resulta estable.
Existen tres series naturales, seg¶un el elemento que les de origen. Se denominan
pues la serie del uranio, del torio y del actinio. Por ejemplo, la serie del uranio, que
comienza con el 238U y termina con el 206Pb puede consultarse en la ¯gura 19.1.

Z
N
Tl Pb Bi Po At Rn Fr Ra Ac Th Pa U
a
b-
145
140
135
130
125
85 90
Figura 19.1: Serie radiactiva del uranio.

Nota ¦ Y cua¶l puede ser la aplicacio¶n de las desintegraciones nucleares?. La
radiactividad tiene m¶ultiples campos de utilizaci¶on. Por ejemplo, el m¶etodo
del 14C permite fechar una muestra midiendo la proporci¶on de 14C frente
al 12C en muestras org¶anicas antiguas y, comparando dicha proporci¶on con
la normal, se calcula cuanto 14C ha deca¶³do. Posteriormente con este dato y
conociendo que la semivida del elemento son unos 5500 a¶os se pueden datar
muestras en un intervalo de unos 1000 a 55000 a~nos. Para muestras de edad
superior o inferior los datos no son signi¯cativos y el proceso no es ¯able.
Otra aplicaci¶on consiste en el uso de is¶otopos radiactivos. Como sabemos
un is¶otopo es qu¶³micamente indistinguible de otro que sea estable. De esta
manera, introduciendo algunos is¶otopos radiactivos en un organismo, ¶este los
asimila como si fueran normales. y as¶³ podemos usarlos como trazadores en
ciertos procesos biol¶ogicos, o para determinar las velocidades de reacciones
qu¶³micas, observar el recorrido de la sangre en el cerebro. . .
19.5. Reacciones nucleares
Cuando los n¶ucleos vencen la repulsi¶on el¶ectrica que los protones generan entre
s¶³ y se sit¶uan en posiciones de alcance de la fuerza nuclear fuerte, es posible que
se produzca un reagrupamiento de los n¶ucleos obteniendo as¶³ unos productos de la
reacci¶on distintos de los originales. Este proceso es el denominado reacci¶on nuclear.
En estas reacciones se conservan la carga y el n¶umero de nucleones, la energ¶³a y
los momentos angular y lineal.
Tipos inportantes de reacciones nucleares son las de ¯si¶on y fusi¶on.
19.5.1. Fisi¶on nuclear
Es la divisi¶on o ruptura de un n¶ucleo pesado en otros dos m¶as ligeros de masas
similares. Es una reacci¶on que espont¶aneamente se produce con gran di¯cultad.
Arti¯cialmente se puede generar bombardeando los n¶ucleos con neutrones. ¶Es-tos,
al no presentar carga, penetran con cierta facilidad en los nucleos y pueden
desencadenar as¶³ un proceso que termina con la ruptura del n¶ucleo original.
Por ejemplo, una reacci¶on nuclear t¶³pica es
235
92 U +10
n !141
56 Kr + 310
n:
En general, las reacciones del 235
92 U pueden esquematizarse como
10
n +235
92 U ! X + Y + 2 o 310
n
siendo los restos de la reacci¶on X e Y n¶uclidos con numeros comprendidos entre los
intervalos (84; 104) y (129; 149).
El hecho de que entre los productos ¯nales de la reacci¶on existan 2 o 3 neutrones
posibilita el hecho de que se produzca una reacci¶on en cadena, es decir, que estos
nuevos neutrones emitidos vuelvan a incidir en nucleos que se ¯sionen, creando
as¶³ m¶as neutrones que. . . y el proceso continua. Cuando sucede una reacci¶on en
cadena de este tipo todo el combustible nuclear se ¯siona muy r¶apidamente y
de manera explosiva liberando enormes cantidades de energ¶³a: hablamos de una
explosi¶on nuclear. Este es el fundamente b¶asico de una bomba at¶omica.
Ahora bien, si logramos reducir el n¶umero medio de neutrones liberados hasta
uno por nucleo ¯sionado, tendremos una reacci¶on controlada. Este es el fundamento
de las reacciones nucleares que suceden en un reactor nuclear de una central at¶omica.

19.5.2. Fusi¶on nuclear
As¶³ como ¯sionar es dividir, fusionar es juntar: en una reacci¶on de fusi¶on se
obtiene un n¶ucleo pesado a partir de dos ligeros. Debido a la repulsi¶on el¶ectrica
entre protones este proceso es m¶as sencillo cuanto m¶as ligeros sean los n¶ucleos
originales. Cuando el n¶ucleo creado tenga menos masa que la suma de los n¶ucleos
originales tendremos que, este defecto de masa se libera como energ¶³a. Este es el
proceso que sucede en todas las estrellas, aut¶enticos hornos de fusi¶on en los que
la enorme presi¶on que genera la gravedad al api~nar estas cantidades gigantescas de
sustancias es su¯ciente para generar espont¶aneamente reacciones de fusi¶on.
Actualmente el proceso de fusi¶on controlada no est¶a dominado (el incontro-lado
s¶³, en las tristemente c¶elebres bombas de hidr¶ogeno o de neutrones) puesto
que se requiere alcanzar y mantener temperaturas del orden de millones de gra-dos
cent¶³grados y no existe ning¶un recipiente que soporte esto, con lo que hay que
contener magn¶eticamente el plasma formado: en cualquier caso el proceso no es
f¶acil.
No obstante, algunas razones para interesarse por el proceso de fusi¶on controlada
son
Es una energ¶³a relativamente limpia: al contrario que en las reacciones de
¯si¶on apenas hay sustancias de desecho peligrosas.
Su rendimiento energ¶etico es muy grande. Por ejemplo en la reacci¶on
21
H +31
H !42
He +10
n
se liberan unos 18MeV.
El carburante que necesita, deuterio y tritio, es f¶acil de obtener. El agua de
mar contiene cantidades ingentes de deuterio.

Ap¶endice A
Esquemas y formulario
A.1. C¶alculo vectorial
1. De¯nici¶on
a) Escalar
b) Vector
1) M¶odulo
2) Direcci¶on
3) Sentido
2. Operaciones con vectores
2x
a) Componentes. ~v = (vx; vy; vz)
q
b) Modulo. ¶j~vj = v =
vy + v2
+ v2
z
c) Vector unitario. ^v = ~v
v
1) (1; 0; 0) = ^{
2) (0; 1; 0) = ^|
3) (0; 0; 1) = ^k
d) Suma. ~a +~b = ~c ) (ax; ay; az) + (bx; by; bz) = (ax + bx; ay + by; az + bz).
Gr¶a¯ca.
e) Producto escalar. ~a ¢~b = ab cos µ = axbx + ayby + azbz
A.2. Cinem¶atica
1. Vector de posici¶on ~r
2. Vector desplazamiento ¢~r = ~r2 ¡~r1
3. Velocidad
a) Media ~v = ~r2¡~r1
t2¡t1
b) Instant¶anea ~v = d
dt~r(t)
4. Aceleraci¶on
a) Media ~a = ~v2¡~v1
t2¡t1
131

AP¶ENDICE A. ESQUEMAS Y FORMULARIO
dt~v(t) = d2
dt2 ~r(t)
b) Instant¶anea ~a = d
c) Tangencial. ~at = dj~vj dt ¢ ^v
d) Normal. ~an = v2
R ¢ ^n; ^n ? ^v
e) Relaciones
1) ~a = ~at +~an
2) a2 = a2t
+ a2
n
A.2.1. Movimiento circular
1. µ es el ¶angulo recorrido en radianes.
2. 2¼rad = 360o
3. Velocidad angular. ! = d
dt µ(t)
4. Aceleraci¶on angular. ® = d
dt!(t)
5. Relaciones magnitudes angulares con lineales
a) v = R!
b) at = R®
c) an = R!2
A.3. Din¶amica
A.3.1. Translaci¶on
1. Leyes de Newton.
a) Ley de inercia
P b)
F ~= m~a
c) Ley de acci¶on y reacci¶on
2. Fuerzas
a) Peso. ~P = m~g.
b) Normal. En rampas N = mg cos µ
c) Rozamiento. Fr = ¹N
d) Tensiones. A ambos lados de una polea perfecta es igual.
3. Momento lineal: ~P = m~v
4. Conservaci¶on del momento lineal.
P
i ~vini
i =
imini
P
imfin
i ~vfin
i
5. Cantidad de movimiento e impulso mec¶anico. ~I = ~Ft = ¢~p
A.3.2. Rotaci¶on
1. Movimiento circular. Fc = mv2
R
2. Aplicacion ¶a curvas con y sin peralte. vmax = p¹gR; vmax = ptan ®gr
3. Momento de un par de fuerzas. M = Fr sin ®
P
4. Momento de inercia. I =
nmnr2n
5. Ecuaci¶on de la din¶amica de rotaci¶on. M = I®

A.4. Trabajo y Energ¶³a
1. Trabajo: concepto intuitivo.
2. Trabajo: concepto matem¶atico:
a) W = Fr cos ®
b) W = ~F ¢ ~r
dt = Fv; P = ~F ¢ ~v
3. Potencia. P = dW
4. Energ¶³a.
a) Concepto intuitivo.
b) Cin¶etica. T = Ec = 1
2mv2
c) Potencial el¶astica. Ep = 1
2Kx2
d) Potencial gravitatoria super¯cie. Ep = mgh
e) Potencial gravitatoria general. Ep = ¡GMm
r
f ) Potencial coulombiana. Ep = KQq
r
g) Teorema de conservaci¶on de la energ¶³a. Ec(A)+Ep(A) = Ec(B)+Ep(B)
A.5. Movimiento arm¶onico simple
1. Ley de Hooke. F = ¡Kx
2. Ecuaci¶on del m.a.s.
a) Ecuaci¶on general. x = Asin(!t + µ)
b) Relaci¶on velocidad posici¶on. v = pA2 ¡ x2
c) Relaci¶on aceleraci¶on posici¶on. a = ¡!2x
3. Qu¶e es !?
a) !2 = K
m
b) Periodo. ! = 2¼
T
c) Frecuencia. ! = 2¼º
d) Relaci¶on periodo y frecuencia. º = T¡1
4. Energ¶³a en un m.a.s.
a) Potencial. Ep = 1
2Kx2
b) Mec¶anica. Etotal = 1
2KA2
5. P¶endulo simple.
a) Relaci¶on con un m.a.s. ! =
pg
l
b) Propiedades. C¶alculo aproximado para amplitudes peque~nas.

A.6. Campo y potencial el¶ectrico y gravitatorio
1. Fuerzas
a) Coulombiana (cargas). ~F = KQq
r2 ^r
b) Newtoniana (masas). ~F = ¡GMm
r2 ^r
2. Campos
a) Electrost¶atico. ~E
= K Q
r2 ^r.
b) Gravitatorio. ~g = ¡GM
r2 ^r.
3. Principio de superposici¶on vectorial. ~Ftotal =
P
i
~Fi.
4. Energ¶³a potencial.
a) Electrost¶atica. Ep = KQq
r .
b) Gravitatoria. Ep = GMm
r .
5. Potencial electrost¶atico. V = KQ
r .
6. Principio de superposici¶on escalar. Vtotal =
P
i Vi.
7. Diferencia de potencial electrost¶atico.
8. Relaci¶on entre la diferencia de potencial y el trabajo. ¢W = q(VA ¡ VB).
9. Relaciones entre campos y fuerzas.
a) Electrost¶atico. ~F = q~E
.
b) Gravitatorio. ~F = m~g.
10. Relaci¶on entre energ¶³a potencial y potencial electrost¶atico. Ep = qV .
11. Flujo (Á = ~E
¢ ~S) y teorema de Gauss.
a) Electrost¶atico. Á = qenc
²0
.
b) Gravitatorio. Á = 4¼Gmenc.
12. Anexos.
a) Signi¯cado de la energ¶³a potencial negativa.
b) Velocidad de escape. Et = 1
2mv2 ¡ GMm
r = 0. Concepto de part¶³culas
ligadas.
c) Relaci¶on (unidimensional) entre el campo y el potencial. E = dV
dx
d) Leyes de Kepler.
e) Resoluci¶on de problemas de sat¶elites. mv2
R = GMm
R2 .

A.7. Circuitos de corriente continua
1. Conductores y aislantes.
2. Intensidad. Amperio. I = dq
dt .
3. Diferencia de potencial. ¢V .
4. Ley de Ohm. Resistencia. ¢V = IR, R = ½ 1
S .
5. Asociaci¶on de resistencias.
a) Asociaci¶on serie. Re =
Pi=n
i=1 Ri
b) Asociaci¶on paralelo. 1
Re
=
Pi=n
i=1
1
Ri
.
6. Instrumentos de medida
a) Amper¶³metros. (Serie).
b) Volt¶³metros. (Paralelo).
7. Trabajo de la corriente el¶ectrica. Ley de Joule. W = I2Rt(J).
8. Potencia de la corriente el¶ectrica. P = I2R.
9. Generadores. Fuerza electromotriz (fem). ¢V = ² ¡ I
P
ri.
10. Motores. Fuerza contra-electromotriz. (fcem). Ley de Ohm generalizada.
P
P ²i =
²0i + I
P
Ri.
11. Redes el¶ectricas. Reglas de Kirchho®.
A.8. Electromagnetismo
1. Campo magn¶etico. ~B
.
2. Flujo magn¶etico. © = ~B
¢ ~S
.
3. Acci¶on de un campo magn¶etico sobre una carga en movimiento. Ley de Lo-rentz.
j ~Fj = qj~vjj ~B
j sin ®.
4. Radio de la ¶orbita de una carga movi¶endose bajo la acci¶on de un campo
magn¶etico. R = mv
qB .
5. Acci¶on de un campo magn¶etico sobre un conductor rectil¶³neo recorrido por
una corriente. Ley de Laplace. j ~Fj = BIl sin ®.
6. Campo magn¶etico creado por una corriente rectil¶³nea. Ley de Biot y Savart.
B = ¹0
2¼
I
r .
7. Campo magn¶etico creado por una espira circular en su centro. B = ¹0
2 IR.
8. Campo magn¶etico creado por un solenoide. B = ¹I n
l .
l = ¹0
9. Fuerza entre corrientes paralelas. De¯nici¶on de amperio. F
2¼
II0
d .

Ap¶endice B
Movimiento de un cuerpo en
el campo gravitatorio bajo el
rozamiento con el aire
B.1. Introducci¶on
Vamos a analizar que sucede cuando dejamos un cuerpo en ca¶³da libre bajo la
acci¶on de la gravedad, pero considerando tambi¶en que existe un rozamiento con la
atm¶osfera, con el aire, de valor Fr = ¡Kv.
B.2. Planteamiento de la ley de Newton
Aplicando la ley de Newton tenemos que
P ~F = m~a. En este caso tomaremos el
sistema de referencia habitual, y al tratarse el problema de una ca¶³da libre, haremos
¶unicamente un tratamiento unidimensional para el eje y.
Las fuerzas que se ejercen sobre el cuerpo que cae son ¶unicamente la fuerza de
la gravedad ¡mg y la de rozamiento ¡Kv1. La constante K la dejaremos indicada,
su valor se mide experimentalmente.
As¶³ pues la ley de Newton se expresar¶a como
¡ mg ¡ Kv = ma: (B.1)
B.3. Interpretaci¶on de la ecuaci¶on de Newton
Vemos que tenemos una ecuaci¶on que relaciona a con v. Ahora bien, la acele-raci
¶on y la velocidad no son magnitudes independientes, ya que una es la derivada
de la otra. Por tanto no podemos despejar tranquilamente a o V , ya que, al estar
relacionadas entre s¶³, esto no ser¶³a una soluci¶on de la ecuaci¶on (B.1). Hemos de
plantear como resolver
¡mg ¡ Kv = m
dv
dt
;
1Hemos de ser conscientes que en este modelo del rozamiento hemos incluido ya el hecho de que
el rozamiento siempre se opone al movimiento. Qu¶e c¶omo sucede esto aqu¶³?, simplemente porque
cuando la velocidad sea positiva ¡Kv ser¶a negativo e ir¶a en sentido contrario al movimiento.
An¶alogamente cuando v 0 tendremos que Fr 0 y tambi¶en se opone al movimiento. Por ¶ultimo
si el cuerpo no se mueve v = 0 y no hay rozamiento.
137

AP¶ENDICE B. MOVIMIENTO DE UN CUERPO EN EL CAMPO GRAVITATORIO BAJO
EL ROZAMIENTO CON EL AIRE
que recibe el nombre de ecuaci¶on diferencial. Aunque el tema de las ecuaciones
diferenciales supera con mucho el nivel y los planteamientos de la f¶³sica general
de este curso, este caso concreto representa, no s¶olo un caso sencillo e inteligible,
sino adem¶as un ejemplo potente y did¶actico de lo que representan las ecuaciones de
Newton para el mundo f¶³sico, raz¶on por la que trataremos este sistema como una
excepci¶on al nivel del curso, pero una excepci¶on muy interesante.
Para resolver esta ecuaci¶on pasemos todos los t¶erminos con v a un lado y los
que tienen t al otro. As¶³ tendremos
¡
mdv
mg + Kv
= dt
lo cual es una forma de acumular todos los t¶erminos en v a un lado y con t bien
separados para nuestra pr¶oxima acci¶on. Integremos ahora ambos miembros entre el
instante t = 0, en el cual suponemos que v = 0 y un instante gen¶erico t.
¡
Z t
0
m
mg + Kv
dv =
Z t
0
dt
.
Esta integral es inmediata d¶andose cuenta de que
d
dt
(mg + Kv) =
K
mg + Kv
, y por tanto tendremos
t]t
0 = ¡
m
K
ln (Kv + mg)
it
0
;
que sabiendo que en t = 0 ten¶³amos v = 0 nos dir¶a que
t = ¡
m
K
ln
µ
Kv + mg
mg
¶
:
Bueno, ahora basta hacer alguna acrobacia matem¶atica y despejar la velocidad,
que es la magnitud que nos interesa, esto se logra exponenciando
e¡Kt
m =
Kv + mg
mg
y despejando
v = ¡
mg
K
³
1 ¡ e¡Kt
m
´
(B.2)
B.4. Conclusi¶on
Interpretar el resultado de la f¶ormula (B.2) es una delicia f¶³sica que nos dir¶a mu-cho
m¶as que todo el desarrollo matem¶atico, m¶as o menos complejo, anterior. Deje-mos
de momento pensar al lector que nos est¶a diciendo esta relaci¶on en general y,
mucho m¶as concretamente que sucede para tiempos muy peque~nos y muy grandes,
es decir, estudiar que signi¯can los casos en los que t ¿ 1 y t ! 1.

Ap¶endice C
Tablas y f¶ormulas ¶utiles
C.1. Introducci¶on
Este ap¶endice est¶a pensado como un complemento o un recordatorio matem¶atico
de algunos conceptos de esta¶³ndole imprescindibles para abordar con ¶exito el estudio
de la f¶³sica. No obstante, si el lector descubre que desconoce una gran parte del
contenido de este ap¶endice, o bien que no comprende la procedencia de las f¶ormulas,
deber¶³a por su cuenta estudiar estas bases hasta su total comprensi¶on.
C.2. C¶alculo complejo
i2 = ¡1 p¡1 = i
(a + bi) ¢ (c + di) = (ac ¡ bd) + (bc + ad)i
a+bi
c+di = ac+bd
c2+d2 + cb¡ad
c2+d2 i
C.3. C¶alculo vectorial
M¶odulo j~aj =
q
a2
x + a2
y + a2z
.
Producto escalar ~a ¢~b = ab cos µ.
Producto vectorial Ver 4.3.4.
C.4. Funciones elementales
C.4.1. Trigonom¶etricas
sin2 t + cos2 t = 1; 8t
sin(a § b) = sin a cos b § cos a sin b
cos(a § b) = cos a cos b ¨ sin a sin b
139

AP¶ENDICE C. TABLAS Y F¶ORMULAS ¶UTILES
C.4.2. Logar¶³tmicas y exponenciales
ln 1 = 0
ln 0 ! ¡1 ln(ab) = ln a + ln b
ln
¡ a
b
¢
= ln a ¡ ln b
ln ab = b ln a
e0 = 1
et ¸ 0; 8t
ea+b = eaeb
eab = eab
C.5. Derivaci¶on
C.5.1. Propiedades generales
Constante d
dtK = 0.
Suma d
dt (f + g) = d
dtf + d
dt g.
Producto por constante d
dt (Kf) = K d
dtf.
Producto d
dt (f ¢ g) =
¡ d
dtf
¢
g + f
¡ d
dt g
¢
.
Divisi¶on d
dt
f
g =
( d
dt f)g¡f( d
dt g)
g2 .
Regla de la cadena d
dtf(g(t)) = ( d
dtf)(g(t)) ¢ d
dt g(t).
Ejemplo de la regla de la cadena d
dt sin(t2) = cos(t2)2t.
C.5.2. Tabla de derivadas
f(t) d
dtf(t) f(t) d
dtf(t)
t 1 tn ntn¡1
pt 1
2pt
sin t cos t
cos t ¡sin t tan t 1
cos2 t
sinh t cosh t cosh t sinh t
ln t 1
x loga t 1
x loga e
at at ln a et et
arcsin t 1 p1¡t2 arc cos t ¡ 1 p1¡x2
arctan t 1
1+t2 arg sinh t 1 pt2+1
arg cosh t 1
§pt2¡1
arg tanh t 1
1¡t2
C.6. Integraci¶on
C.6.1. De¯nici¶on y propiedades
Se de¯ne
R
f(t)dt = F(t) + C si se cumple que d
dtF(t) = f(t). Algunas propie-dades
son:
Nula
R
0dt = C donde C es una constante cualesquiera.
Constante
R
Kf(t)dt = K
R
f(t)dt,

Suma
R
(f(t) + g(t)) dt =
R
f(t)dt +
R
g(t)dt.
La integral de un producto de dos funciones es
Z
u(t)dv(t) = u(t)v(t) ¡
Z
v(t)du(t):
C.6.2. Tabla de integrales
R
tndt = tn+1
R n+1 + C; n6= ¡1 dt
t R = ln jtj + C
R etdt = et + C
R sin tdt = ¡cos t + C
Rcos tdt = sin t + C dt
R = tan t + C cos2 t dt R p1= arcsin t + C
¡t2 R tan x = ¡
¡ln pt2 jcos tj + ¢
C pdt = ln
t + 1
t2¡1
¡ R + C dt
1+t2 = arctan t + C

Ap¶endice D
Agradecimientos
El autor quiere agradecer la colaboraci¶on, a la hora de buscar y corregir las
erratas a todos sus (sufridos) alumnos, y m¶as especialmente por su dedicaci¶on en
dicha b¶usqueda a:
Beatriz Est¶³valiz Mu~noz Gonzalez.
Elena Casillas Mill¶an.
Ma de la Concepci¶on de Le¶on L¶opez.
Miguel ¶Angel Morillo Lozano.
Miguel Torres Dur¶an.
143

AP¶ENDICE D. AGRADECIMIENTOS

Fisica general para leer

Más contenido relacionado

La actualidad más candente

Similar a Fisica general para leer

Último

Fisica general para leer