Descargado 40 veces
Subido porMiguel Sancho
Geométria computacional: Polígonos y-monótonos
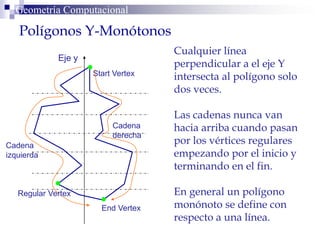
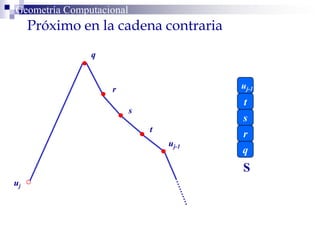
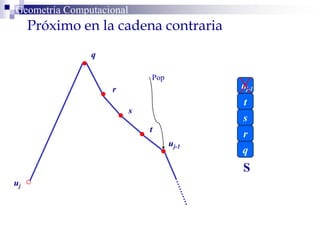
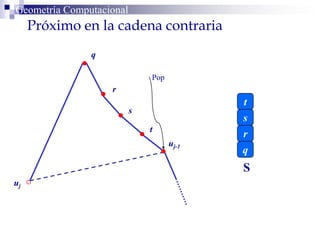
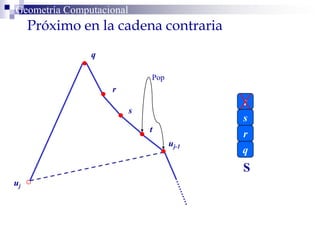
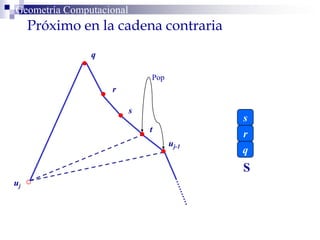
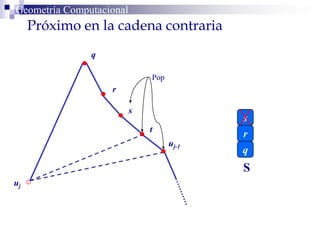
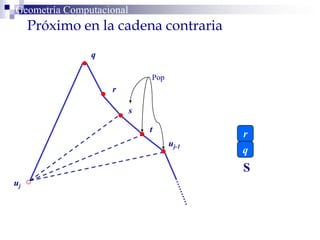
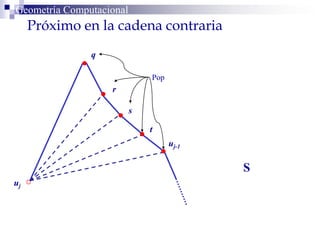
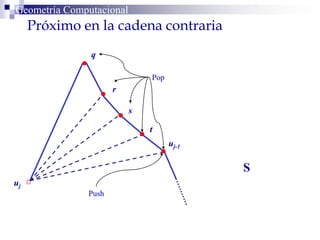
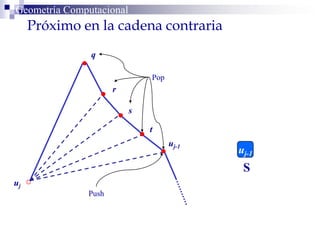
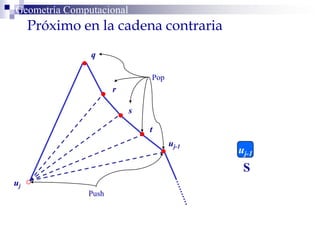
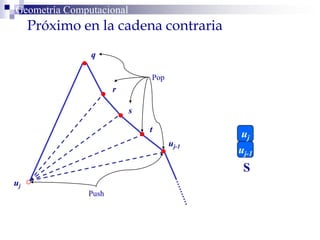
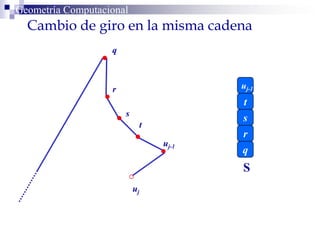
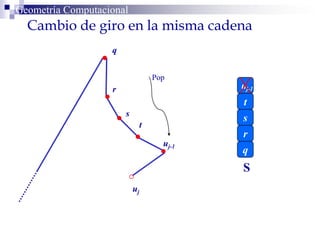
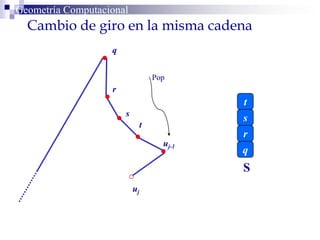
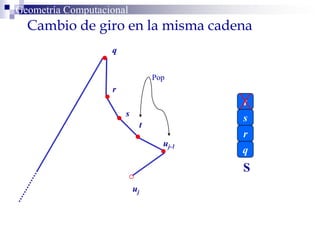
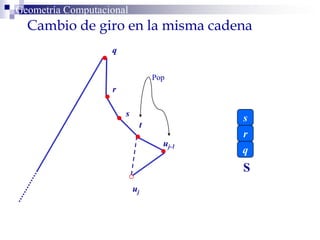
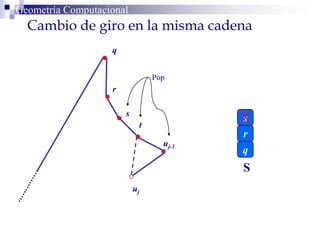
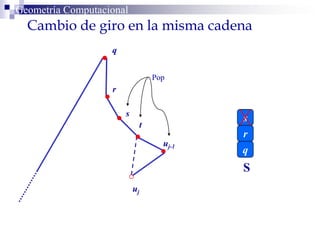
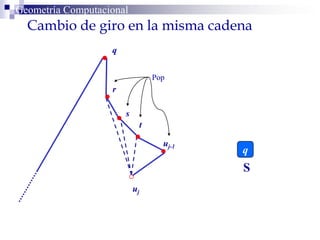
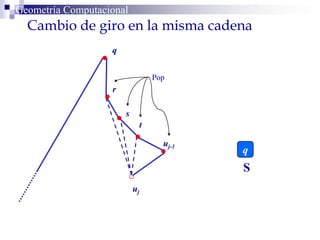
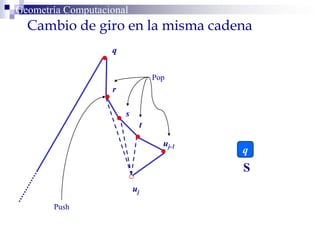
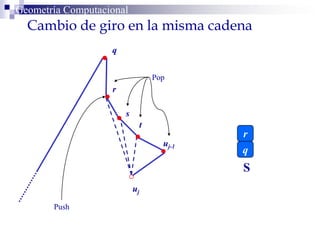
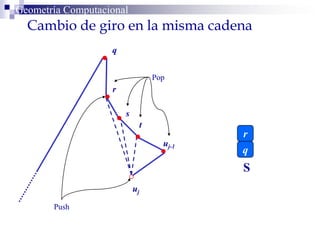
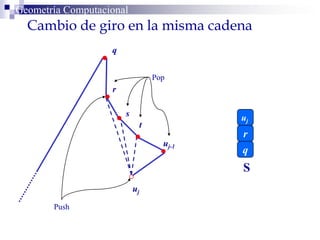
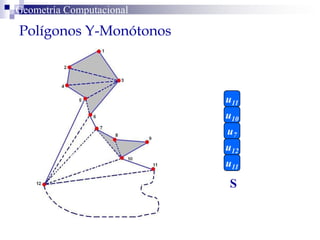
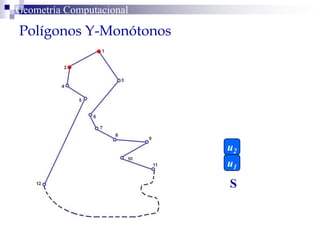
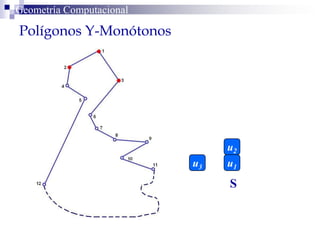
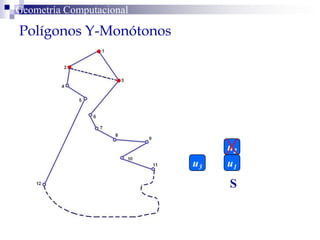
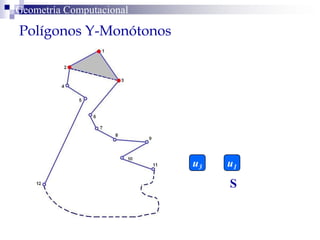
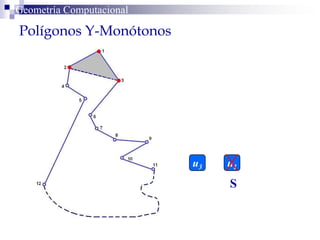
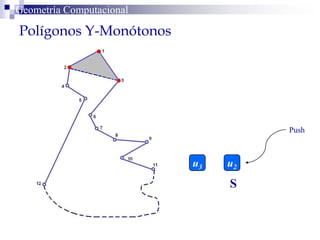
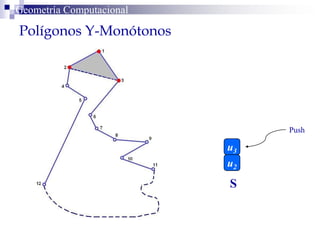
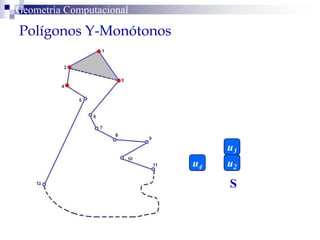
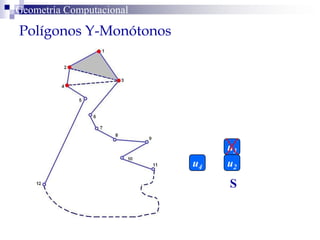
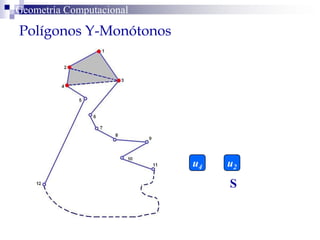
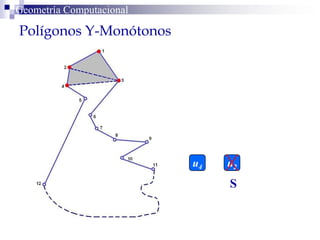
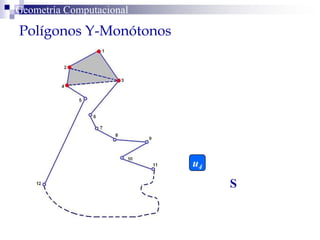
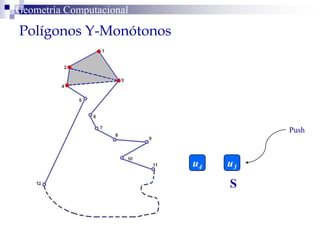
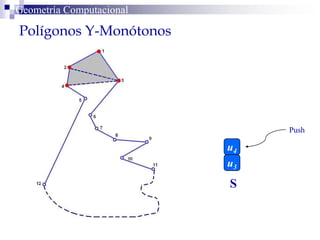
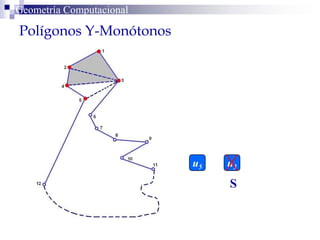
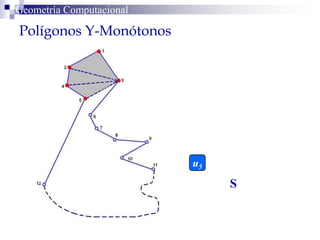
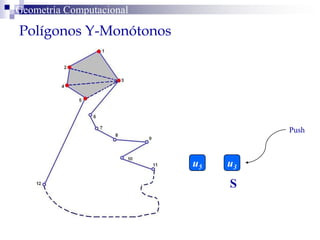
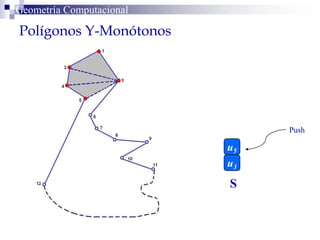
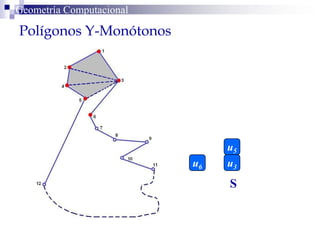
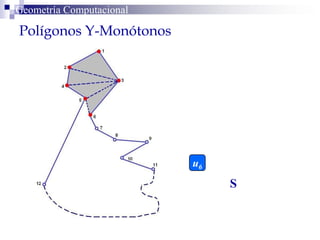
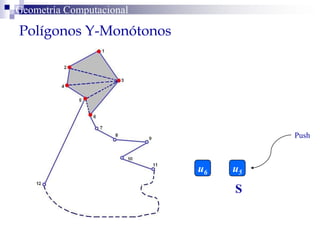
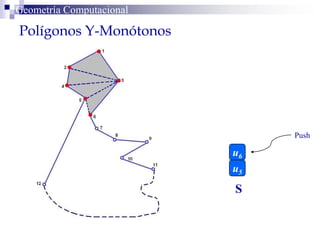
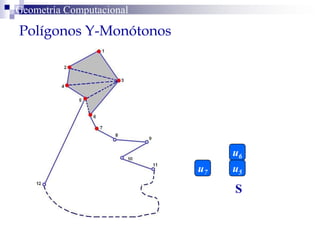
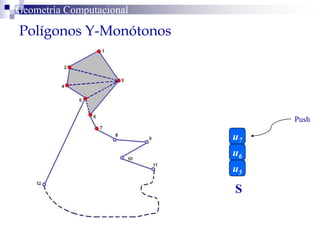
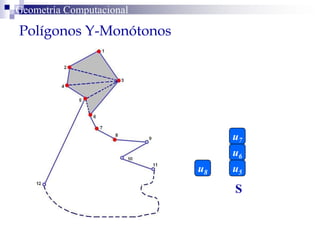
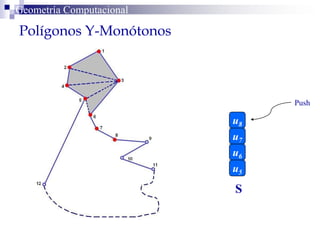
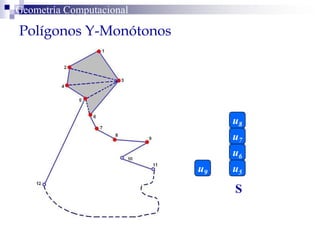
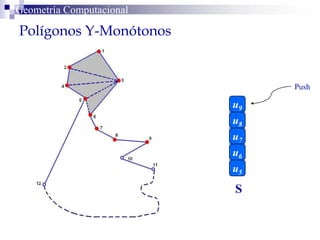
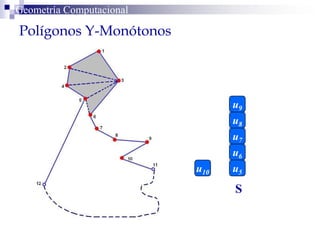
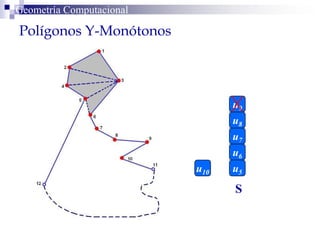
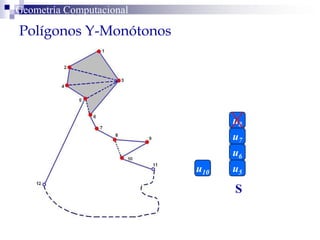
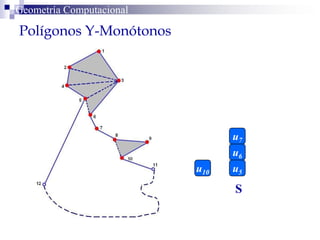
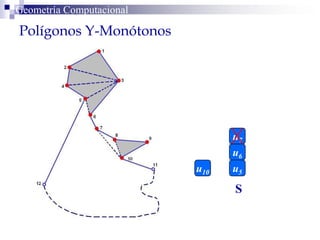
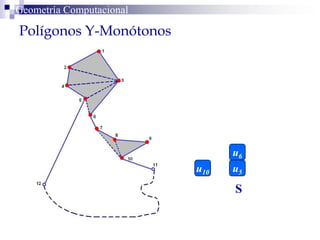
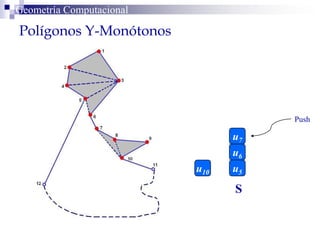
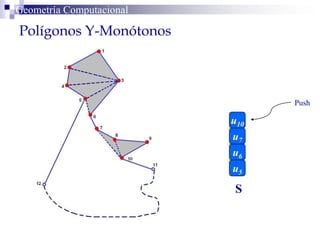
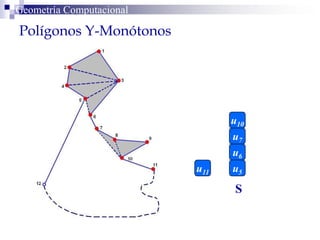
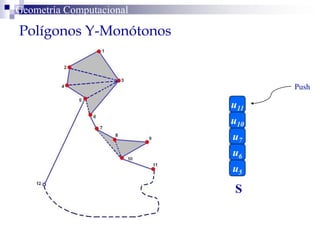
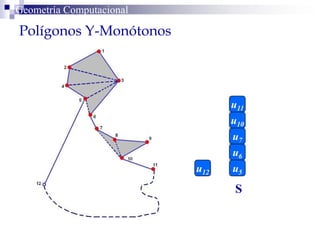
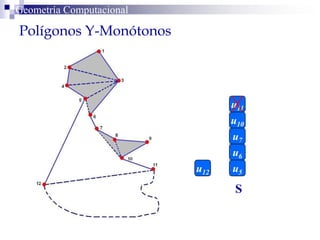
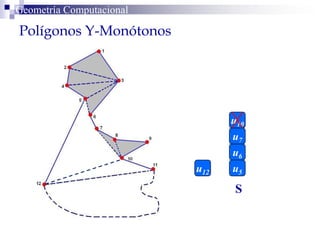
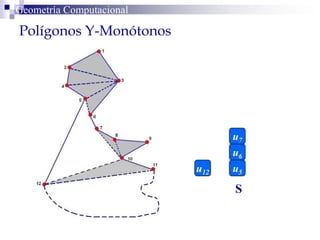
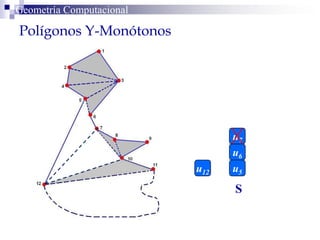
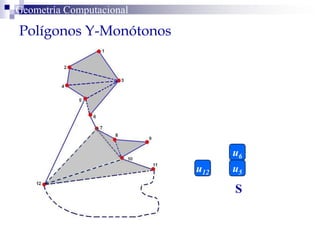
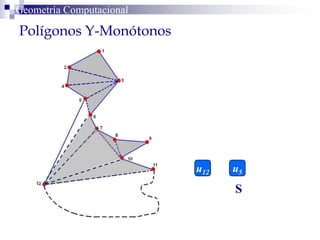
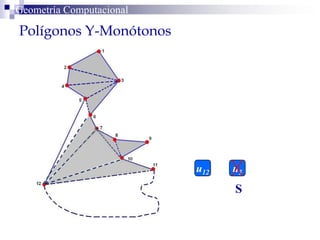
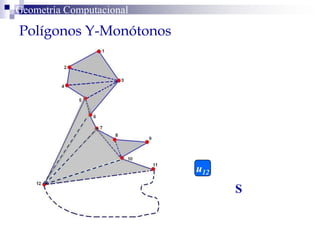
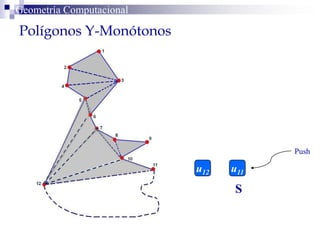
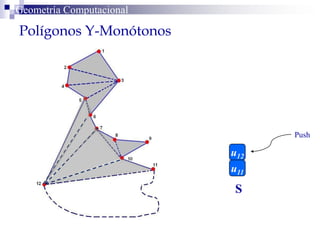
El documento describe un algoritmo para la triangulación de polígonos y-monótonos utilizando una técnica de recorrido de vértices y una pila. Se establece un proceso paso a paso que incluye la verificación de la posibilidad de trazar diagonales y la inserción en una estructura de datos. El análisis de tiempo total del algoritmo es O(n), destacando su eficiencia en la manipulación de vértices.
Más contenido relacionado
La actualidad más candente
Similar a Geométria computacional: Polígonos y-monótonos
![Modelos%20 Geom% C3% A9tricos%20y%20 Fractales[1]](https://cdn.slidesharecdn.com/ss_thumbnails/modelos20geomc3a9tricos20y20fractales1-100207160109-phpapp01-thumbnail.jpg?width=640&height=640&fit=bounds)
Geométria computacional: Polígonos y-monótonos
- 1.
- 2. Polígonos Y-Monótonos Eje y Cadena izquierda EndVertex Start Vertex Cualquier línea perpendicular a el eje Y intersecta al polígono solo dos veces. Las cadenas nunca van hacia arriba cuando pasan por los vértices regulares empezando por el inicio y terminando en el fin. En general un polígono monónoto se define con respecto a una línea. Geometría Computacional Cadena derecha Regular Vertex
- 3. Triangulanción de unPolígono Y-Monótono Geometría Computacional Usar la técnica de algoritmo Greddy (glotón) recorriendo los vértices en orden descendente por el eje Y. Si desde el vértice actual no se puede trazar una diagonal, se adiciona a una pila S. Para verificar si se puede trazar una diagonal se chequea con los dos vértices en el tope de la pila S. Cuando se pueda trazar una diagonal se trazan todas aquellas que sean posibles sacando vértices de la pila S. En la pila S siempre deben quedar al menos dos vértices para chequear con el próximo vértice.
- 4. Geometría Computacional Próximo enla cadena contraria t s r q uj q r s t uj-1 S uj-1
- 5. Geometría Computacional Próximo enla cadena contraria t s r q uj uj-1 Pop q r s t uj-1 S
- 6. Geometría Computacional Próximo enla cadena contraria t s r q uj uj-1 Pop q r s t S
- 7. t Geometría Computacional Próximo enla cadena contraria t s r q uj uj-1 Pop q r s S
- 8. Geometría Computacional Próximo enla cadena contraria t s r q uj uj-1 Pop q r s S
- 9. Geometría Computacional Próximo enla cadena contraria t s r q uj uj-1 Pop q r s S
- 10. Geometría Computacional Próximo enla cadena contraria t s r q uj uj-1 Pop q r S
- 11. Geometría Computacional Próximo enla cadena contraria t s r q uj uj-1 Pop q r S
- 12. Geometría Computacional Próximo enla cadena contraria t s r q uj uj-1 Pop q S
- 13. Geometría Computacional Próximo enla cadena contraria t s r q uj uj-1 Pop q S
- 14. Geometría Computacional Próximo enla cadena contraria t s r q uj uj-1 Pop S
- 15. Geometría Computacional Próximo enla cadena contraria t s r q uj uj-1 Pop S Push
- 16. Geometría Computacional Próximo enla cadena contraria t s r q uj uj-1 Pop Push uj-1 S
- 17. Geometría Computacional Próximo enla cadena contraria t s r q uj uj-1 Pop Push uj-1 S
- 18. Geometría Computacional Próximo enla cadena contraria t s r q uj uj-1 Pop Push uj-1 S uj
- 19. Geometría Computacional Cambio degiro en la misma cadena uj-1 t s r q uj q r s t uj-1 S
- 20. Geometría Computacional Cambio degiro en la misma cadena uj-1 t s r q uj q r s t uj-1 S Pop
- 21. Geometría Computacional Cambio degiro en la misma cadena uj-1 t s r q uj q r s t S Pop
- 22. Geometría Computacional Cambio degiro en la misma cadena uj-1 t s r q uj q r s t S Pop
- 23. Geometría Computacional Cambio degiro en la misma cadena uj-1 t s r q uj q r s S Pop
- 24. Geometría Computacional Cambio degiro en la misma cadena uj-1 t s r q uj q r s S Pop
- 25. Geometría Computacional Cambio degiro en la misma cadena uj-1 t s r q uj q r s S Pop
- 26. Geometría Computacional Cambio degiro en la misma cadena uj-1 t s r q uj q r S Pop
- 27. Geometría Computacional Cambio degiro en la misma cadena uj-1 t s r q uj q r S Pop
- 28. Geometría Computacional Cambio degiro en la misma cadena uj-1 t s r q uj q S Pop
- 29. Geometría Computacional Cambio degiro en la misma cadena uj-1 t s r q uj q S Pop
- 30. Geometría Computacional Cambio degiro en la misma cadena uj-1 t s r q uj q S Pop Push
- 31. Geometría Computacional Cambio degiro en la misma cadena uj-1 t s r q uj q S Pop Push r
- 32. Geometría Computacional Cambio degiro en la misma cadena uj-1 t s r q uj q S Pop Push r
- 33. Geometría Computacional Cambio degiro en la misma cadena uj-1 t s r q uj q S Pop Push r uj
- 34. TriangulateMonotonePolygon(P) Input: A y-monotonepolygon P sotored in a DCEL D. Output: A triangulation of P stored in D. 1. Merge all vertices of P into one sequence sorted on decreasing y coordinate. 2. Initialize an empty stack S and push u1 and u2 onto it. 3. for j ← 3 to n – 1 4. if uj and Top(S) are on different chains 5. then v = Pop(S) 6. while !IsEmpty(S) 7. insert into D a diagonal from uj to v 8. v = Pop(S) 9. Push(S, uj-1) 10. else v = Pop(S) 11. while !IsEmpty(S) and Top(S) is visible from uj 12. v = Pop(S) 13. insert into D a diagonal from uj to v 14. Push(S, v) 15. Push(S, uj) 16. Add diagonals from un to all stack vertices except the first and the last one. Geometría Computacional
- 35.
- 36.
- 37.
- 38.
- 39.
- 40.
- 41.
- 42.
- 43.
- 44.
- 45.
- 46.
- 47.
- 48.
- 49.
- 50.
- 51.
- 52.
- 53.
- 54.
- 55.
- 56.
- 57.
- 58.
- 59.
- 60.
- 61.
- 62.
- 63.
- 64.
- 65.
- 66.
- 67.
- 68.
- 69.
- 70.
- 71.
- 72.
- 73.
- 74.
- 75.
- 76.
- 77.
- 78.
- 79.
- 80.
- 81.
- 82.
- 83.
- 84.
- 85.
- 86.
- 87.
- 88. Triangulación de unPolígono Y-Monótono Como se parte del polígono representado en una DCEL, mezclar los vértices de forma ordenada toma un tiempo O(n). Realizando un análisis amortizado de las operaciones se obtiene que el tiempo total del algoritmo es O(n). Geometría Computacional