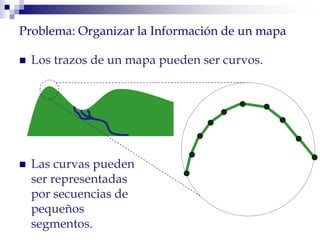
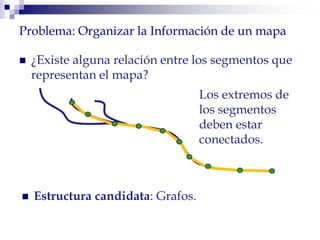
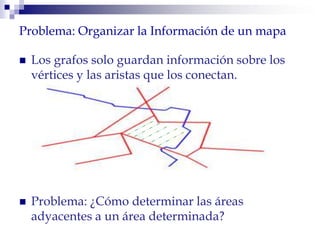
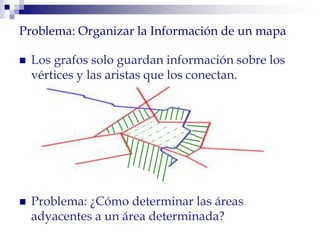
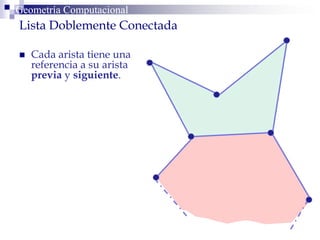
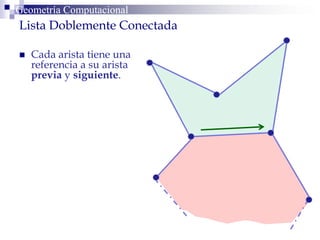
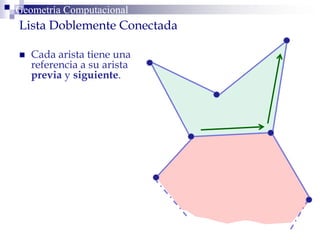
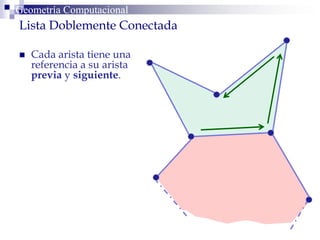
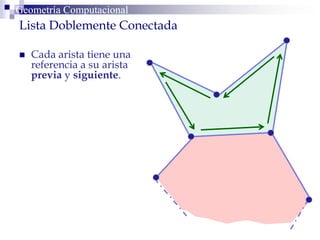
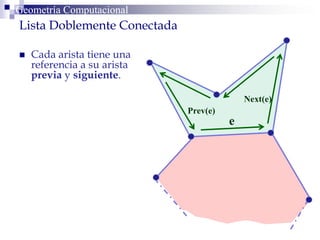
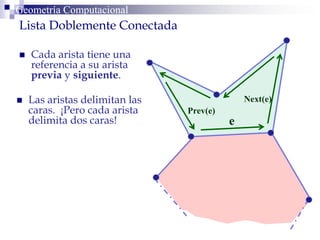
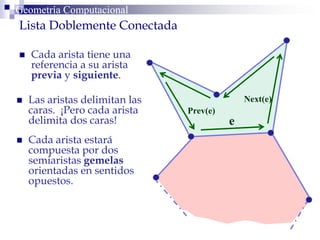
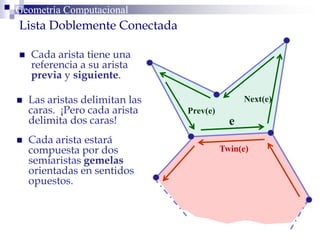
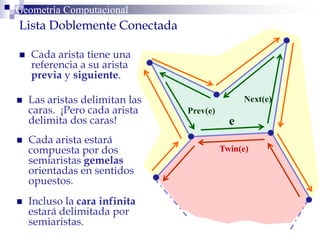
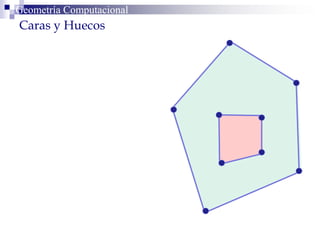
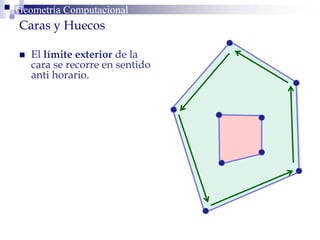
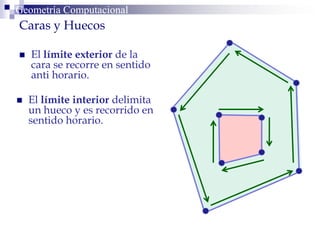
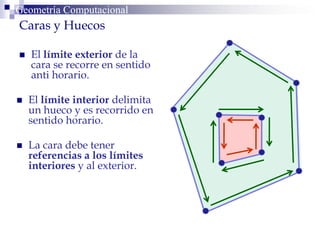
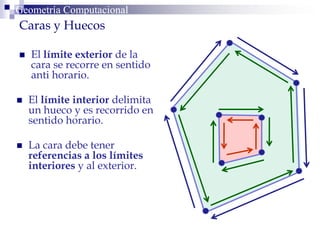
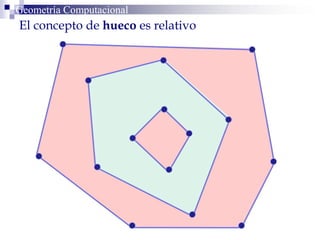
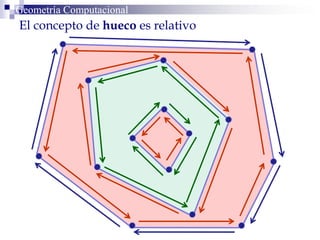
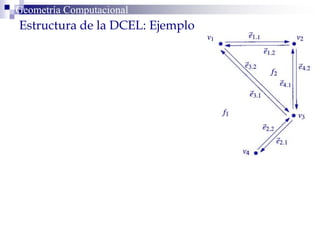
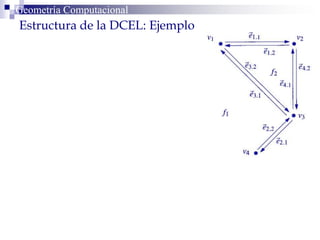
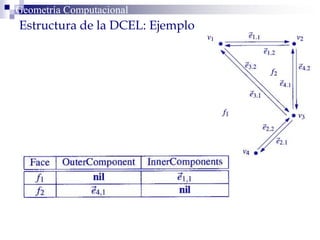
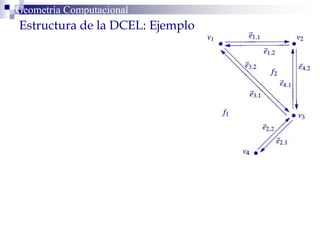
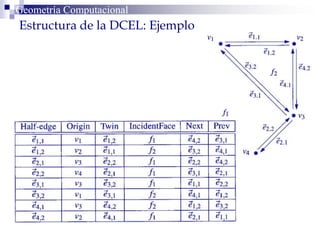
Este documento describe la estructura de datos DCEL (Doubly Connected Edge List) para representar subdivisiones planares. La DCEL almacena información topológica y geométrica de vértices, aristas y caras de una subdivisión planar. Cada arista está compuesta por dos semiaristas gemelas orientadas en sentidos opuestos. La DCEL permite realizar operaciones eficientes como determinar áreas adyacentes y vértices incidentes.