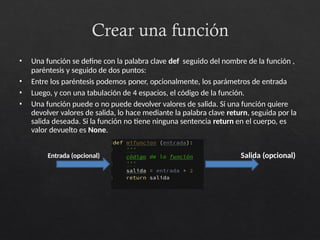
El documento describe los fundamentos de la programación en Python, incluyendo tipos de datos como números, cadenas, listas, y booleanos, así como la forma de definir variables y asignarles valores. Se aborda también la operación de operadores aritméticos y su precedencia, así como el uso de lógica booleana para la toma de decisiones en algoritmos. Además, se discuten las normas para nombrar variables y las características de las funciones que manipulan datos.



![Tipos de datos
Ferran Juan Baruel
Ciències de la Computació / 2017
Tipos
Numéricos
Básicos
Estructurados
Enteros
Alfanuméricos String
Reales
Diccionarios
Listas, tuplas
Conjuntos
Set
FrozenSet
Logicos o Boolean
Decimal, binario, valores pertenecientes a
los enteros con signo (23, 0010010)
Valores pertenecientes al conjunto de los
Reales (0.76, 1.9878*103)
Letras, símbolos (‘hola’ , ‘nombre’)
Dos Únicos valores True o False
(Verdadero o falso)
Una única variable contiene varios valores
de diferentes tipos básicos [1,8.9,’hola’]
Una única variable contiene pares de
clave-valor { clave1:valor1, …}
Conjuntos ordenados de valores](https://image.slidesharecdn.com/1-241120195201-24c3a94e/85/LAS-FUNCIONES-Y-VariablesOperadoresFunciones-pptx-4-320.jpg)
![Tipos de datos
Ferran Juan Baruel
Ciències de la Computació / 2017
Tipos
Numéricos
Básicos
Estructurados
Enteros
Alfanuméricos String
Reales
Diccionarios
Listas, tuplas
Conjuntos
Set
FrozenSet
Logicos o Boolean
Decimal, binario, valores pertenecientes a
los enteros con signo (23 ó 0010010)
Valores pertenecientes al conjunto de los
Reales (0.76, 1.9878*103)
Letras, símbolos (‘hola’ , ‘nombre’)
Dos Únicos valores True o False
(Verdadero o falso)
Una única variable contiene varios valores
de diferentes tipos básicos [1,8.9,’hola’]
Una única variable contiene pares de
clave-valor { clave1:valor1, …}
Conjuntos ordenados de valores](https://image.slidesharecdn.com/1-241120195201-24c3a94e/85/LAS-FUNCIONES-Y-VariablesOperadoresFunciones-pptx-5-320.jpg)
![Tipos numéricos:
Codificación, Rango y precisión
Ferran Juan Baruel
Ciències de la Computació / 2017
•
[1] Ferran Virgos Codificacion](https://image.slidesharecdn.com/1-241120195201-24c3a94e/85/LAS-FUNCIONES-Y-VariablesOperadoresFunciones-pptx-6-320.jpg)

![Tipos de datos
Ferran Juan Baruel
Ciències de la Computació / 2017
Tipos
Numéricos
Básicos
Estructurados
Enteros
Alfanuméricos String
Reales
Diccionarios
Listas, tuplas
Conjuntos
Set
FrozenSet
Logicos o Boolean
Decimal, binario, valores pertenecientes a
los enteros con signo (23, 0010010)
Valores pertenecientes al conjunto de los
Reales (0.76, 1.9878*103)
Letras, símbolos (‘hola’ , ‘nombre’)
Dos Únicos valores True o False
(Verdadero o falso)
Una única variable contiene varios valores
de diferentes tipos básicos [1,8.9,’hola’]
Una única variable contiene pares de
clave-valor { clave1:valor1, …}
Conjuntos ordenados de valores](https://image.slidesharecdn.com/1-241120195201-24c3a94e/85/LAS-FUNCIONES-Y-VariablesOperadoresFunciones-pptx-8-320.jpg)



![Tipos de datos
Tipos
Numéricos
Básicos
Estructurados
Enteros
Alfanuméricos String
Reales
Diccionarios
Listas, tuplas
Conjuntos
Set
FrozenSet
Logicos o Boolean
Decimal, binario, valores pertenecientes a
los enteros con signo (23, 0010010)
Valores pertenecientes al conjunto de los
Reales (0.76, 1.9878*103)
Letras, símbolos (‘hola’ , ‘nombre’)
Dos Únicos valores True o False
(Verdadero o falso)
Una única variable contiene varios valores
de diferentes tipos básicos [1,8.9,’hola’]
Una única variable contiene pares de
clave-valor { clave1:valor1, …}
Conjuntos ordenados de valores](https://image.slidesharecdn.com/1-241120195201-24c3a94e/85/LAS-FUNCIONES-Y-VariablesOperadoresFunciones-pptx-13-320.jpg)























![Evaluación de variables como lógicas
Ferran Juan Baruel
Ciències de la Computació / 2017
• Cualquier variable puede ser evaluada como una variable lógica o
Booleana, para su uso en estrtucturas de decision
• Los siguientes valores pueden ser evaluados como False
– None,
– False
– Un valor cero de cualquier tipo numérico: 0, 0.0, …
– colecciones y secuencias vacías: '', (), [], {}, range(0)
– Las operaciones y funciones que tienen siempre un resultado booleano
devuelven 0 o False para falso y 1 o True para verdadero
– En cualquier otro caso, la variable puede evaluarse como True
• Más información: https://docs.python.org/3/library/stdtypes.html#truth-value-testing](https://image.slidesharecdn.com/1-241120195201-24c3a94e/85/LAS-FUNCIONES-Y-VariablesOperadoresFunciones-pptx-37-320.jpg)