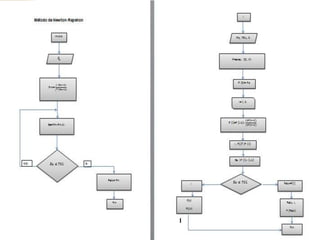
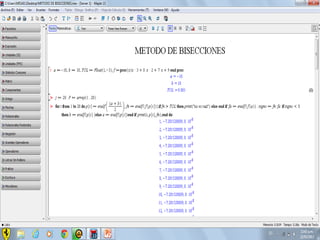
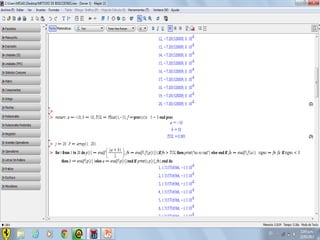
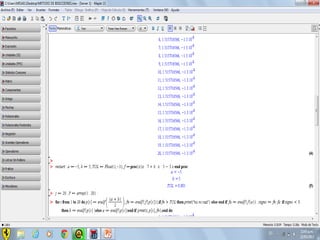
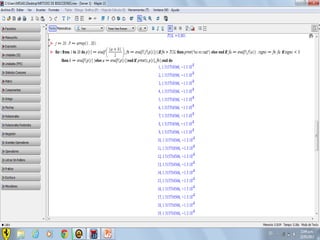
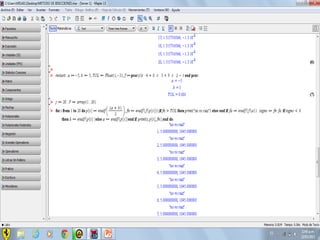
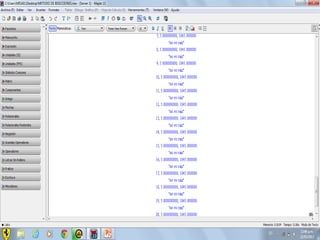
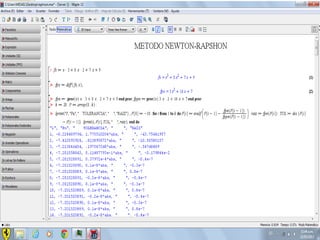
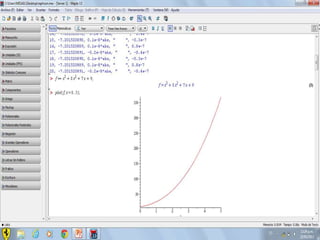
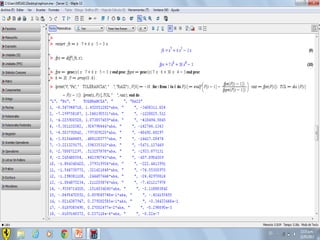
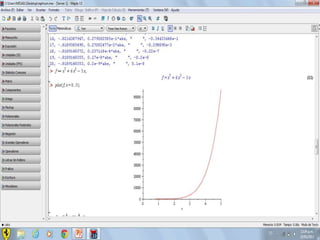
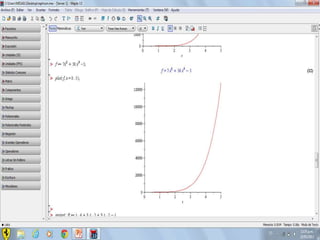
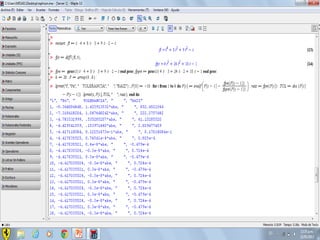
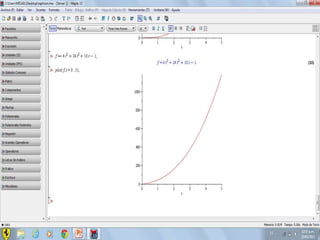
Este documento compara los métodos numéricos de bisecciones y Newton-Raphson para encontrar las raíces de una función. Presenta tablas que muestran los resultados iterativos de aplicar ambos métodos a diferentes funciones, incluyendo los valores de A, B, P, F(P) y la tolerancia en cada paso. Concluye que el uso de software matemático hace que la solución de problemas sea más sencilla y permita abordar problemas más complejos.

1. MIGUEL ÁNGEL SÁNCHEZ
DÍAS
ING RODOLFO ALCANTARA
ROSALES
METODOS NUMERICOS

2.  JUSTIFICACIÓN
 CON EL USO DE SOFTWARE
MATEMÁTICO, ES POSIBLE CONOCER
LAS RAÍCES DE UNA FUNCIÓN EN
FORMA ANALÍTICA Y GRAFICA PARA
DETERMINAR EL COMPORTAMIENTO
DE LAS VARIABLES INVOLUCRADAS.

3. 

4. Método de bisecciones
Iteración A B P F(p) Signo f(a)*f(p) Tolerancia
1 -10 10 -7.20152 (a+b)/2 8*10-8 10-3
2 -10 10 -7.20152 (a+b)/2 8*10-8 10-3
3 -10 10 -720152 (a+b)/2 8*10-8 10-3
4 -10 10 -7.20152 (a+b)/2 8*10-8 10-3
5 -10 10 -7.20152 (a+b)/2 8*10-8 10-3
Iteración A B P F(p) Signo f(a)*f(p) Tolerancia
1 -10 10 1.51751 (a+b)/2 1.3*10-8 10-3
2 -10 10 1.51751 (a+b)/2 1.3*10-8 10-3
3 -10 10 1.51751 (a+b)/2 1.3*10-8 10-3
4 -10 10 1.51751 (a+b)/2 1.3*10-8 10-3
5 -10 10 1.51751 (a+b)/2 1.3*10-8 10-3
Iteración A B P F(p) Signo f(a)*f(p) Tolerancia
1 -10 10 1.51751 (a+b)/2 1.3*10-8 10-3
2 -10 10 1.51751 (a+b)/2 1.3*10-8 10-3
3 -10 10 1.51751 (a+b)/2 1.3*10-8 10-3
4 -10 10 1.51751 (a+b)/2 1.3*10-8 10-3
5 -10 10 1.51751 (a+b)/2 1.3*10-8 10-3
Iteración A B P F(p) Signo f(a)*f(p) Tolerancia
1 -10 10 5 (a+b)/2 1845 10-3
2 -10 10 5 (a+b)/2 1845 10-3
3 -10 10 5 (a+b)/2 1845 10-3
4 -10 10 5 (a+b)/2 1845 10-3
5 -10 10 5 (a+b)/2 1845 10-3

5. Método de newton rapshon
Iteración Ea
1 -10 -8.224489796 1.775510204 1.775510204
2 -8.224489796 -7.41059392 0.813895872 .813895872
3 -7.41059392 -7.213046656 0.197547268 .197547268
4 -7.213046656 -7.20155886 0.11487793e-1 0.11487793e-1
Iteración Ea
1 -10 -7.999840000 2.000160000 2.000160000
2 -7.999840000 -6.399481344 1.600358656 1.600358656
3 -6.399481344 -6.399481344 1.280850252 1.280850252
4 -6.399481344 -4.092574076 1.026057016 1.026057016
Iteración Ea
1 -10 -8.547948718 1.452051282 1.452051282
2 -8.547948718 -7.299758187 1.248190531 1.248190531
3 -7.299758187 -6.225900528 1.073857659 1.073857659
4 -6.225900528 -5.301102082 0.924798446 0.924798446
Iteración Ea
1 -10 -8.366086468 1.633913532 1.633913532
2 -8.366086468 -7.318618206 1.047468262 1.047468262
3 -7.318618206 -6.783332999 0.535285207 0.535285207
4 -6.783332999 -6.629361559 0.153971440 0.153971440

7. METODO DE
BISECCIONES

14. METODO NEWTON
RAPSHON

27. Conclusiones:
 La solución de problemas en este tipo
de software es muy sencilla y nos
facilita la solución de problemas de
mayor complejidad