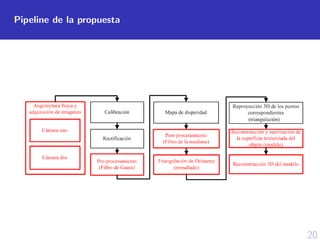
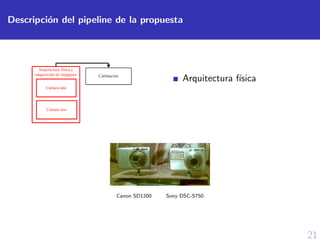
Este documento presenta un modelo para la reconstrucción 3D de objetos a partir de dos imágenes estéreo. Propone un pipeline que incluye la adquisición de imágenes, calibración, rectificación, cálculo del mapa de disparidad, generación de malla 3D y texturizado del modelo. El método se prueba en objetos como un cubo mágico, oso de peluche y rostro humano, obteniendo resultados aceptables a pesar de limitaciones como iluminación y tamaño de vecindario. Se concluye que es necesario mejorar





![3
Motivaci´on y contexto
Limitaciones en la ´epoca pre-renacentista para crear en 3D.
Los art´ıstas en la ´epoca del renacimiento y la profundidad.
Los puntos de fuga y la tridimensionalidad.
(a) Jes´us entrando
a Jerusal´en
(b) La Escuela de Atenas
Figura: Pintura pre-renacentista y renacentista [Ma et al., 2004].](https://image.slidesharecdn.com/defesatesisguillermo-201102184122/85/Sustentacion-de-tesis-espanol-6-320.jpg)
![4
Planteamiento del problema
Arquitectura f´ısica, posici´on, distribuci´on e iluminaci´on.
(a) Una sola c´amara
[Cipolla et al., 2010]
(b) Iluminaci´on artificial
[VISGRAF., 2012]](https://image.slidesharecdn.com/defesatesisguillermo-201102184122/85/Sustentacion-de-tesis-espanol-7-320.jpg)
![5
Planteamiento del problema (cont...)
Figura: ¿ C´omo obtener los par´ametros necesarios para realizar un
mapeamiento de un objeto al plano imagen ? [Faugeras, 1993].](https://image.slidesharecdn.com/defesatesisguillermo-201102184122/85/Sustentacion-de-tesis-espanol-8-320.jpg)
![6
Planteamiento del problema (cont...)
Figura: ¿ C´omo hallar los puntos correspondientes ? [Szeliski, 2011].](https://image.slidesharecdn.com/defesatesisguillermo-201102184122/85/Sustentacion-de-tesis-espanol-9-320.jpg)
![7
Planteamiento del problema (cont...)
Figura: ¿ C´omo hallar un punto en 3D de cada par de puntos
correspondientes ? [Szeliski, 2011].](https://image.slidesharecdn.com/defesatesisguillermo-201102184122/85/Sustentacion-de-tesis-espanol-10-320.jpg)
![8
Planteamiento del problema (cont...)
Figura: ¿ C´omo reconstruir y suavizar una superficie a partir de una nube
de puntos ? [Hartley and Zisserman, 2004].](https://image.slidesharecdn.com/defesatesisguillermo-201102184122/85/Sustentacion-de-tesis-espanol-11-320.jpg)



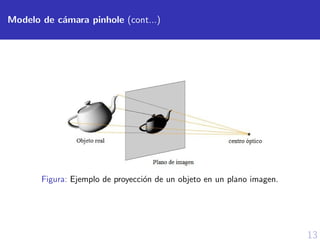
![12
Modelo de c´amara pinhole
Ayuda a entender la formaci´on de una imagen desde un punto de
vista geom´etrico.
Partes del modelo de c´amara pinhole: centro ´optico(o), distancia
focal(f ) y plano imagen(I).
x = ¯op ∩ I x ∈ R2
, p ∈ R3
Figura: Modelo de c´amara pinhole [Ma et al., 2004].](https://image.slidesharecdn.com/defesatesisguillermo-201102184122/85/Sustentacion-de-tesis-espanol-15-320.jpg)

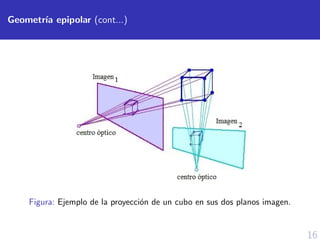
![15
Geometr´ıa epipolar
Estudia la relaci´on geom´etrica y an´alisis matem´atico de un punto
3D p en sus planos imagen.
Figura: Analisis geom´etrico de dos vistas [Ma et al., 2004].](https://image.slidesharecdn.com/defesatesisguillermo-201102184122/85/Sustentacion-de-tesis-espanol-18-320.jpg)
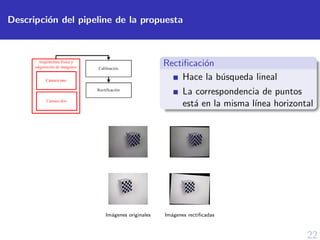
![17
Rectificaci´on
Figura: Rectificaci´on del par de im´agenes est´ereo [Fusiello et al., 2000].](https://image.slidesharecdn.com/defesatesisguillermo-201102184122/85/Sustentacion-de-tesis-espanol-20-320.jpg)
![18
C´alculo de disparidad
(a) (b) Mapa de disparidad
(a - b) Par de im´agenes de Tsukuba [Scharstein and Szeliski, 2002].](https://image.slidesharecdn.com/defesatesisguillermo-201102184122/85/Sustentacion-de-tesis-espanol-21-320.jpg)

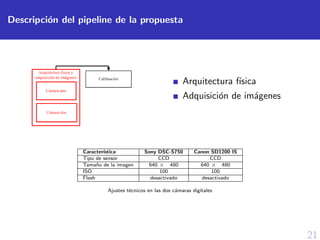
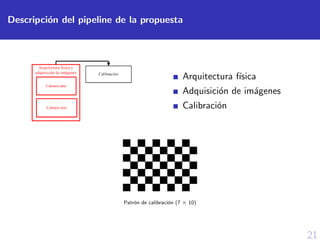
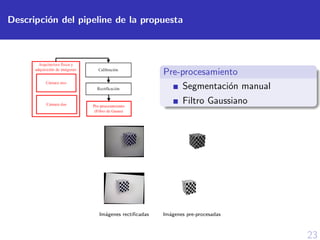
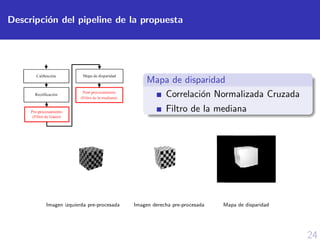
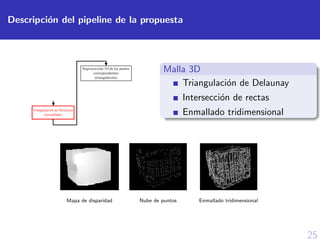

















![40
Trabajos futuros
Crear un ambiente con las adecuadas
condiciones para la calibraci´on, ilumi-
naci´on y adquisici´on de im´agenes.
Arquitectura f´ısica e iluminaci´on artificial [Bradley et al., 2008]](https://image.slidesharecdn.com/defesatesisguillermo-201102184122/85/Sustentacion-de-tesis-espanol-52-320.jpg)
![40
Trabajos futuros
Crear un ambiente con las adecuadas
condiciones para la calibraci´on, ilumi-
naci´on y adquisici´on de im´agenes.
Arquitectura f´ısica e iluminaci´on artificial [Bradley et al., 2008]
Hacer una extensi´on a
m´ultiples c´amaras.
M´ultiples vistas [Hartley and Zisserman, 2004]](https://image.slidesharecdn.com/defesatesisguillermo-201102184122/85/Sustentacion-de-tesis-espanol-53-320.jpg)








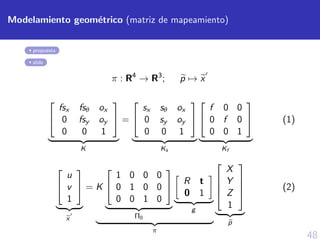


![49
Ecuaciones de la Geometr´ıa Epipolar
slide
Restricci´on epipolar
xT
2 Fx1 = 0
Matriz Fundamental
F = K−T
2 EK−1
1
Matriz esencial
E = [t]x R](https://image.slidesharecdn.com/defesatesisguillermo-201102184122/85/Sustentacion-de-tesis-espanol-65-320.jpg)
![49
Ecuaciones de la Geometr´ıa Epipolar
slide
Restricci´on epipolar
xT
2 Fx1 = 0
Matriz Fundamental
F = K−T
2 EK−1
1
Matriz esencial
E = [t]x R
Matriz antisim´etrica
[t]x =
0 −c b
c 0 −a
−b a 0
(3)](https://image.slidesharecdn.com/defesatesisguillermo-201102184122/85/Sustentacion-de-tesis-espanol-66-320.jpg)







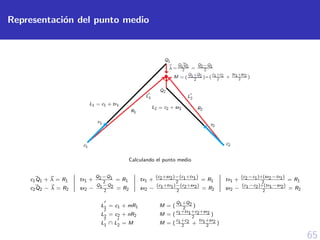
![57
Planteamiento inicial de la rectificaci´on
propuesta
slide
La variable π representa a la matriz de mapeamiento
x ∼= π p (18)
Factorizaci´on QR de la matriz π
π = K[R | t] (19)
La matriz π se re-escribe como:
π =
qT
1 |q14
qT
2 |q24
qT
3 |q34
= Q|q (20)](https://image.slidesharecdn.com/defesatesisguillermo-201102184122/85/Sustentacion-de-tesis-espanol-74-320.jpg)
![58
Planteamiento inicial de la rectificaci´on (cont...)
Las coordenadas del centro ´optico c est´a definido como:
c = −Q−1
q (21)
Se hace un despeje de la ecuaci´on 21 en funci´on de q.
π = [Q| − Qc] (22)](https://image.slidesharecdn.com/defesatesisguillermo-201102184122/85/Sustentacion-de-tesis-espanol-75-320.jpg)
![59
Desarrollo de la rectificaci´on
Matriz de transformaci´on
xr1 = λ Qr1Q−1
o1
Tl
xo1 λ ∈ R+
(23)
Para lo cual:
πo1 = [Qo1|qo1] πo1 MPP imagen izquierda inicial
πr1 = [Qr1 |qr1] πr1 MPP imagen izquierda rectificada](https://image.slidesharecdn.com/defesatesisguillermo-201102184122/85/Sustentacion-de-tesis-espanol-76-320.jpg)
![60
Pasos para hallar la matriz de transformaci´on
Se hace una factorizaci´on QR de las matrices iniciales
π1 = K[R | − R c1] π1 MPP de la imagen izquierda
π2 = K[R | − R c2] π2 MPP de la imagen derecha
(24)
Los centros ´opticos se hallan con la ecuaci´on 21
La matriz K es la matriz de par´ametros intr´ınsecos
La matriz de rotaci´on R es la misma para ambas matrices de
mapeamiento](https://image.slidesharecdn.com/defesatesisguillermo-201102184122/85/Sustentacion-de-tesis-espanol-77-320.jpg)







![69
Pseudo-c´odigo del algoritmo de c´alculo de disparidad
dispComp(imDerecha,imIzquierda,maxDisp)
1 thNorm ← escalar ∗ (2 ∗ r + 1)
2 for i = 1 + r to col − r do
3 for j = 1 + r to fil − maxDisp − r do
5 pBase ← imDerecha(i − r : i + r, j − r : j + r)
6 pBase ← pBase − promedio(pBase)
7 nBase ← norma(pBase)
8 if nBase <= thNorm then
9 continue
10 end if
11 pBase ← pBase/nBase
12 for sh = 1 to maxDisp do
13 pShift ← imIzquierda(i − r : i + r, j + sh − r : j + sh + r)
14 pShift ← pShift − promedio(pShift)
15 nShift ← norma(pShift)
16 if nShift <= thNorm then
17 corr[sh] ← 0
18 continue
19 end if
20 corr[sh] ← sum((pShift/nShift). ∗ (pBase))
21 end for
22 [valor indice] ← max(corr)
23 if valor == 0 then
24 imDisp[i, j] ← 0
25 else
26 imDisp[i, j] ← indice
27 end if
28 end for
29 end for
30 return(imDisp)](https://image.slidesharecdn.com/defesatesisguillermo-201102184122/85/Sustentacion-de-tesis-espanol-86-320.jpg)


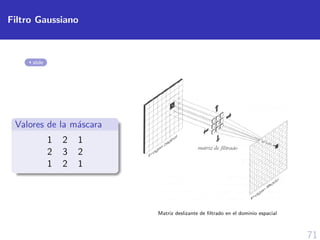

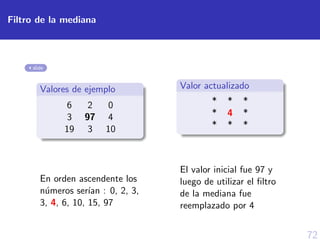
![73
Suavizaci´on del Laplaciano
slide
Calcula la posici´on de un
v´ertice q a partir del
promedio de los v´ertices
adyacentes.
Ejemplo:
3,6
5,4
9,2
14,3
16,10
7,6
———
54, 31
p(9,5) = 54
6 , 31
6
Representaci´on de la suavizaci´on del Laplaciano [Vollmer et al., 1999]](https://image.slidesharecdn.com/defesatesisguillermo-201102184122/85/Sustentacion-de-tesis-espanol-92-320.jpg)