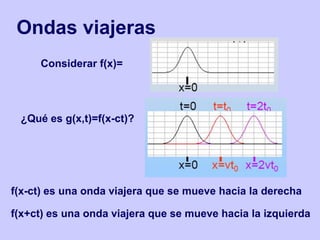
Este documento describe diferentes tipos de ondas mecánicas y electromagnéticas. Explica que las ondas transportan energía y momento lineal pero no materia. Se clasifican las ondas según cómo y qué vibra, y según su forma. También define conceptos básicos como foco, frente de ondas y rayos para ondas esféricas, planas y viajeras.

1. Ondas mecánicas

2. Ondas y materia
Las ondas transportan
• Energía
• Momento lineal
Las ondas no transportan
• Materia

3. Ejemplo: ondas en una cuerda tensa
Un punto de una cuerda:
• oscila
• No se traslada

4. Clasificación de ondas
¿Cómo vibra?
•Transversal
• Longitudinal
¿Qué vibra?
• Ondas mecánicas
• Ondas electromagnéticas (OEM)

5. Clasificación de ondas ¿Qué forma?
Pulso
Tren de ondas
• Finito
• Infinito

6. Conceptos básicos
• Foco
• Frente de ondas
• Rayos

7. Ondas esféricas y circulares y
ondas planas
Esféricas y circulares Planas

8. f(x-ct) es una onda viajera que se mueve hacia la derecha
Considerar f(x)=
Ondas viajeras
¿Qué es g(x,t)=f(x-ct)?
f(x+ct) es una onda viajera que se mueve hacia la izquierda

9. Ecuación diferencial de ondas
Comprobar que para u(x,t)=f(x-vt) o u=f(x+vt)
0
1
2
2
2
2
2






t
u
v
x
u

10. Ondas armónicas o sinusoidales
u(x,t)=A cos(kx-t+0)

11. Periodicidad con respecto a x
En t=0, es solamente función de x:
u(x,0)=A cos(kx+0)
)
(
Amplitud A )
(
onda
de
Número
2
)
(
onda
de
Longitud
k

 

12. Periodicidad con respecto a t
En x=0, es solo función del tiempo:
u(0,t)=A cos(-t+0)=A cos(t-0)
)
(
Amplitud A
)
(
angular
frecuencia
2
)
(
frecuencia
1
)
(
Periodo





f
T

13. Conceptos de ondas armónicas
u=A cos(kx-t +0)
Amplitud A, Fase  =  (x,t)=kx-t +0
Longitud de onda , period T
Frequencia
Frequencia angular
Número de onda
Velocidad de propagación
Dirección de propagación +x
T
f
1



2

k
k
T
v




T


2


14. Intensidad de una onda
Intensidad: energía por unidad de tiempo y de área que
fluye a traves de una superficie perpendicular a la
dirección de progación de la onda
t
Sv
x
S
E u
u d
)
d
(
d 
 

v
S
P
t
S
E
I u




d
d
I=u v

15. Densidad de energía e intensidad
de una onda mecánica
2
2
2
,
2
1
)
(
2
1
A
m
u
m
E
E máx
máx
c 






 

 v
I u

)
sin( 0


 





 t
kx
A
t
u
u

2
2
2
1
A
V
E
u 
 



v
A
I 2
2
2
1


Intensidad de una
onda mecánica

16. Potencia e intensidad
IS
P 
En una onda esférica I disminuye con el cuadrado
de la distancia:

 2
4 R
I
P 
En una onda plana I es constante
2
2
1
1 S
I
S
I
P 

2
2
2
2
1
1 R
I
R
I 
Otros casos se analizan de forma similar

17. El sonido
v
A
I 2
2
2
1


Onda mecánica, se puede describir como
onda de presión, con amplitud
Nivel de intensidad sonora en decibelios:
vA
p 

0
v
p
I

2
0
2
1

0
log
10
I
I


2
12
0 W/m
10

I es el umbral
mínimo de audición de los
seres humanos
m/s
340
kg/m
29
.
1 3


v


18. Niveles de intensidad sonora