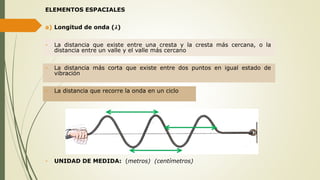
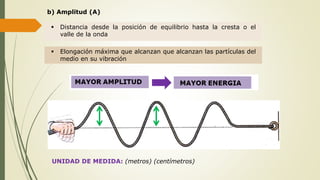
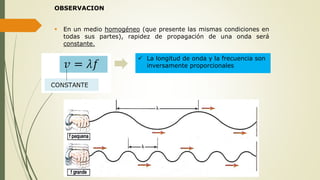
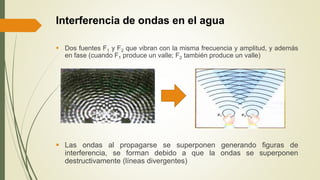
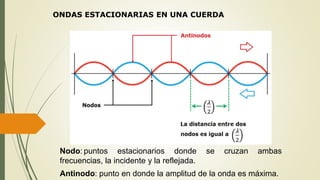
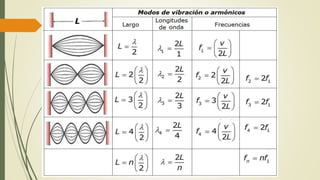
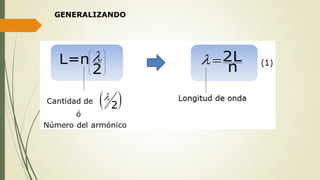
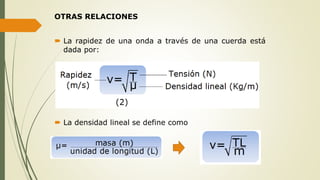
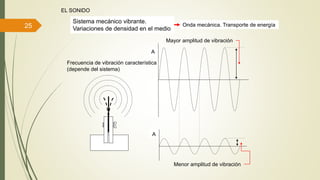
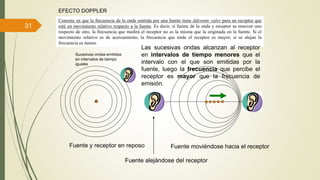
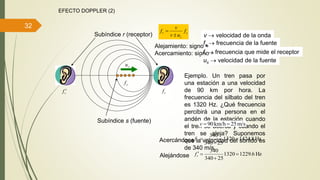
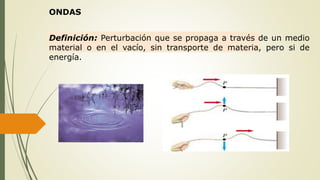
Este documento define las ondas y describe sus características principales. Explica que las ondas son perturbaciones que se propagan a través de un medio sin transporte de materia, pero sí de energía. Clasifica las ondas según su naturaleza, forma de propagarse y sentido de propagación. Describe elementos temporales como período y frecuencia, y elementos espaciales como longitud de onda y amplitud. Explica conceptos como rapidez de propagación, interferencia, ondas estacionarias y resonancia.

1. ONDAS

2. ONDAS
Definición: Perturbación que se propaga a través de un medio
material o en el vacío, sin transporte de materia, pero si de
energía.

3. PULSOS Y ONDAS
PULSO
ONDA Sucesión de pulsos
Si la sucesión de pulsos se produce a intervalos regulares de tiempo,

4. FORMAS DE CLASIFICAR UNA ONDA
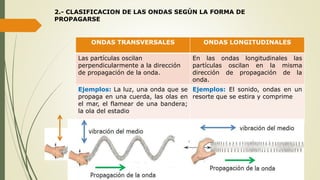
1.-CLASIFICACION DE LAS ONDAS SEGÚN SU NATURALEZA:
ONDAS MECÁNICAS ONDAS ELECTROMAGNÉTICAS
Son las que necesitan un medio
material para propagarse
El movimiento oscilatorio de cargas
eléctricas genera ondas
electromagnéticas, que pueden
propagarse incluso en el vacío, a la
velocidad de 3x108 [m/s]
Ejemplos: Ondas sísmicas, ondas
en la superficie del agua, ondas
sonoras, ondas en una cuerda
Ejemplos: Ondas de radio, la luz.
Rayos ultravioleta, ondas de
telecomunicaciones

5. 2.- CLASIFICACION DE LAS ONDAS SEGÚN LA FORMA DE
PROPAGARSE
ONDAS TRANSVERSALES ONDAS LONGITUDINALES
Las partículas oscilan
perpendicularmente a la dirección
de propagación de la onda.
En las ondas longitudinales las
partículas oscilan en la misma
dirección de propagación de la
onda.
Ejemplos: La luz, una onda que se
propaga en una cuerda, las olas en
el mar, el flamear de una bandera;
la ola del estadio
Ejemplos: El sonido, ondas en un
resorte que se estira y comprime

6. 3.- CLASIFICACION DE LAS ONDAS SEGÚN SU SENTIDO DE PROPAGACION
ONDAS VIAJERAS ONDAS ESTACIONARIAS
Son ondas que se propagan
partiendo desde la fuente , sin
volver atrás
Se producen cuando una onda
“rebota” sobre una superficie y se
interpone sobre si misa. Se
requiere un medio de propagación
acotado
Por ejemplo:
la luz del Sol que viaja por el
espacio y llega a nosotros; las
ondas de televisión televisores del
país
Por ejemplo:
Una onda sonora que se propague
en una sala cerrada, una onda
propagándose en una cuerda de
guitarra

7. ELEMENTOS DE UNA ONDA

8. ELEMENTOS TEMPORALES
PERIODO (T) FRECUENCIA (f)
Tiempo que emplea la onda en
completar un ciclo completo
Cantidad de ciclos por unidad de
tiempo
Unidad de medida:
[segundos]
Unidad de medida:
Hertz  [Hz] = [ciclos/s]
[1/s] = [s-1]
RELACIÓN ENTRE PERIDO Y FRECUENCIA
Son inversamente proporcionales 

9. ELEMENTOS ESPACIALES
a) Longitud de onda (𝝀)
- La distancia que existe entre una cresta y la cresta más cercana, o la
distancia entre un valle y el valle más cercano
- La distancia más corta que existe entre dos puntos en igual estado de
vibración
- La distancia que recorre la onda en un ciclo
- UNIDAD DE MEDIDA: (metros) (centímetros)

10. b) Amplitud (A)
 Distancia desde la posición de equilibrio hasta la cresta o el
valle de la onda
 Elongación máxima que alcanzan que alcanzan las partículas del
medio en su vibración
UNIDAD DE MEDIDA: (metros) (centímetros)

11. RAPIDEZ DE PROPAGACION DE UNA ONDA
 Es la distancia recorrida por la onda, por cada unidad de tiempo
 En un tiempo igual a T, la onda recorre una distancia igual a su
propia longitud de onda 𝜆
 Como f=1/T, entonces:

12. OBSERVACION
 En un medio homogéneo (que presente las mismas condiciones en
todas sus partes), rapidez de propagación de una onda será
constante.
 La longitud de onda y la frecuencia son
inversamente proporcionales

13. Interferencia
 Cuando dos o más
ondas se encuentran en
una misma región del
espacio al mismo
tiempo, se superponen
y generan una onda
resultante cuya amplitud
es la suma de las
amplitudes de las ondas
que interfieren.

14. Interferencia de ondas en el agua
 Dos fuentes F1 y F2 que vibran con la misma frecuencia y amplitud, y además
en fase (cuando F1 produce un valle; F2 también produce un valle)
 Las ondas al propagarse se superponen generando figuras de
interferencia, se forman debido a que la ondas se superponen
destructivamente (líneas divergentes)

15. Onda Estacionaria
 Una onda estacionaria es el resultado de la superposición de dos
movimientos ondulatorios armónicos de igual amplitud y
frecuencia que se propagan en sentidos opuestos a través de un
medio.
 Pero la onda estacionaria NO ES una onda viajera, puesto que
su ecuación no contiene ningún término de la forma kx-t.
 Por ejemplo para ilustrar la formación de ondas estacionarias el
caso de una onda transversal que se propaga en el sentido de
izquierda a derecha () en una cuerda sujeta por sus extremos;
esta onda incide sobre el extremo derecho y se produce una
onda reflejada que se propaga en el sentido de derecha a
izquierda (). La onda reflejada tiene una diferencia de fase de 
radianes respecto a la incidente. La superposición de las dos
ondas, incidente y reflejada, da lugar, en ciertas condiciones, a
ondas estacionarias.

16. ONDAS ESTACIONARIAS EN UNA CUERDA
Nodo: puntos estacionarios donde se cruzan ambas
frecuencias, la incidente y la reflejada.
Antinodo: punto en donde la amplitud de la onda es máxima.

18. GENERALIZANDO

19.  Las frecuencias de vibración en los distintos armónicos o
modos de vibración; son múltiplos enteros de la
frecuencia fundamental
 Otro ejemplo de “cuantizacion”

20. OTRAS RELACIONES
 La rapidez de una onda a través de una cuerda está
dada por:
 La densidad lineal se define como

21.  De la relación
 Reemplazando (1) y (2) en (3)
 Frecuencia de vibración de una cuerda en función del
largo L y la tensión T (μ y n constantes)

22. Resonancia
Se produce cuando el periodo de vibración coincide con
el periodo de vibración característico de un cuerpo.
El cuerpo vibra aumentando de forma progresiva la
amplitud del movimiento.
El resonador de Helmholtz

25. 25
EL SONIDO
Sistema mecánico vibrante.
Variaciones de densidad en el medio
Frecuencia de vibración característica
(depende del sistema)
Onda mecánica. Transporte de energía
P
P
Mayor amplitud de vibración
Menor amplitud de vibración
A
A

26. 26
330
335
340
345
350
355
360
0 5 10 15 20 25 30 35 40
Velocidad del sonido en el aire en funcion de la temperatura
v (m/s)
T (C)
Figura 1
EL SONIDO / 2
Máximos de presión
Mínimos de presión
ONDAS DE PRESIÓN
La velocidad del
sonido aumenta
cuando aumenta
la rigidez del
medio. Sólidos
Líquidos
Gases
Velocidaddelsonido
M
TR
v


-1
kg·mol0289.0M
Aire:
-1-1
·molJ·K314.8R

27. 27
LAS ONDAS TRANSPORTAN ENERGÍA: ONDAS SONORAS
En el sonido la vibración de las partículas ocurre en la misma dirección de
la transmisión de la onda: son ondas longitudinales. A la vibración de las
partículas del medio les corresponden desplazamientos s(x,t) cuyo valor
máximo llamaremos aquí s0:
   2/cos, 0   txkstxs
En la transmisión del sonido, la masa vibrando
en cada punto será la que corresponda al
volumen elemental V que contiene a dicho
punto, esto es m = ρ V. La energía asociada
con esta vibración es:
A tales desplazamientos les corresponden variaciones de
presión alrededor de un valor de equilibrio p0, que se
encuentran desfasadas /2 rad respecto a ellos
   txkptxp cos, 0 
donde 00 svp 
22
0
2
1
smE  22
0
2
1
 sV 
En términos de energía por unidad de volumen
22
0
2
1
 s
V
E



Energía movimiento armónico
0p
/ tx

28. 28
INTENSIDAD DE LAS ONDAS: APLICACIÓN AL SONIDO
Para una fuente que emite ondas en todas direcciones, la energía se distribuye uniformemente en una
superficie esférica A, de radio r. La intensidad de una onda, I, es la potencia por unidad de área, o energía
por unidad de tiempo y unidad de área, que incide perpendicularmente a la dirección de propagación
A
E
I


Frentes de onda
Rayos
Fuente
t
E
E



r
t
r
A
V
E
E





v
V
E
A
E
I




22
0
2
1
 s
V
E



00 svp 
v
p
s 0
0


V
Vt
E



 rA
tV
E




vA
V
E



(transparencia anterior)
(transparenc
ia anterior)
vsI
2
1 22
0 
2
1
2
1 2
02
2
0
v
p
v
v
p
I



 






0p
/ tx
2/0pprms 
Valor rms (valor eficaz)
2
v
p
I rms



29. 29
NIVELES
• Al definir un nivel es preciso indicar la base del logaritmo, la cantidad de referencia y el tipo de nivel
(por ejemplo, nivel de presión sonora, nivel de potencia sonora o nivel de intensidad)
• Un NIVEL es el logaritmo de la razón de una cantidad dada respecto de una cantidad de referencia
del mismo tipo.







0
10log10
W
W
LW
Potencia de referencia: W0
= 10-12
W
)120log10(
10
log10 1210 





 
W
W
LW
Nivel de potencia sonora: Emisión de sonido por una fuente







0
10log10
I
I
LI
Intensidad de referencia: I0 =
10-12
w/m2• Umbral de audición: 10-12
w/m2 (0 dB)
• Umbral de dolor: 1 w/m2 (120 dB)
Nivel de intensidad sonora: Recepción del sonido de una fuente
)120log10(
10
log10 1210 





 
I
I
LI
Nivel de presión sonora: Recepción del sonido de una fuente
Pa102referenciadepresión 5
refp


















refref p
p
p
p
L rmsrms
P 10
2
10 log20log10
(definido en términos del cociente de presiones al
cuadrado porque la intensidad sonora es
proporcional al cuadrado de la presión sonora)

30. 30







0
10log10
I
I
LI







0
102
2
log10
I
I
L I
2log10log10 10
0
10 






I
I
dB33log10
0
10 





 IL
I
I
NIVELES: EJEMPLO
a) Si se dobla la intensidad de un sonido, ¿qué variación sufre el nivel de intensidad?
b) Si se multiplica por 10 la intensidad de un sonido, ¿qué variación sufre el nivel de intensidad?
Se dobla la intensidad







0
1010
10
log10
I
I
L I
10log10log10 10
0
10 






I
I
dB1010log10
0
10 





 IL
I
I
Se multiplica por 10 la intensidad

31. 31
Consiste en que la frecuencia de la onda emitida por una fuente tiene diferente valor para un receptor que
esté en movimiento relativo respecto a la fuente. Es decir, si fuente de la onda y receptor se mueven uno
respecto de otro, la frecuencia que medirá el receptor no es la misma que la originada en la fuente. Si el
movimiento relativo es de acercamiento, la frecuencia que mide el receptor es mayor; si se alejan la
frecuencia es menor.
EFECTO DOPPLER
Fuente y receptor en reposo Fuente moviéndose hacia el receptor
Las sucesivas ondas alcanzan al receptor
en intervalos de tiempo menores que el
intervalo con el que son emitidas por la
fuente, luego la frecuencia que percibe el
receptor es mayor que la frecuencia de
emisión.
Fuente alejándose del receptor
Sucesivas ondas emitidas
en intervalos de tiempo
iguales

32. 32
EFECTO DOPPLER (2)
s
s
r f
uv
v
f


v  velocidad de la onda
fr  frecuencia que mide el receptor
fs  frecuencia de la fuente
Subíndice s (fuente)
Subíndice r (receptor)
Alejamiento: signo +
Acercamiento: signo 
us  velocidad de la fuente
Ejemplo. Un tren pasa por
una estación a una velocidad
de 90 km por hora. La
frecuencia del silbato del tren
es 1320 Hz. ¿Qué frecuencia
percibirá una persona en el
andén de la estación cuando
el tren se acerca y cuando el
tren se aleja? Suponemos
que la velocidad del sonido es
de 340 m/s.
m/s25km/h90 v
rf
sf
su
rf 
Hz8.14241320
25340
340


rfAcercándose
Hz6.12291320
25340
340


rfAlejándose

33. 33
Galaxia de Andrómeda
Galaxia de Pegaso
EFECTO DOPPLER (3)
El desplazamiento al rojo