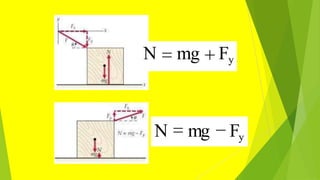
La tercera ley de Newton establece que para cada acción existe una reacción igual y opuesta. Si un cuerpo A ejerce una fuerza sobre un cuerpo B, entonces B ejerce una fuerza igual pero en dirección opuesta sobre A. Estas fuerzas actúan sobre diferentes cuerpos y se conocen como un par de fuerzas de acción y reacción.